guest post by Blake Pollard
Hi! My name is Blake S. Pollard. I am a physics graduate student working under Professor Baez at the University of California, Riverside. I studied Applied Physics as an undergraduate at Columbia University. As an undergraduate my research was more on the environmental side; working as a researcher at the Water Center, a part of the Earth Institute at Columbia University, I developed methods using time-series satellite data to keep track of irrigated agriculture over northwestern India for the past decade.
I am passionate about physics, but have the desire to apply my skills in more terrestrial settings. That is why I decided to come to UC Riverside and work with Professor Baez on some potentially more practical cross-disciplinary problems. Before starting work on my PhD I spent a year surfing in Hawaii, where I also worked in experimental particle physics at the University of Hawaii at Manoa. My current interests (besides passing my classes) lie in exploring potential applications of the analogy between information and entropy, as well as in understanding parallels between statistical, stochastic, and quantum mechanics.
Glacial cycles are one essential feature of Earth’s climate dynamics over timescales on the order of 100’s of kiloyears (kyr). It is often accepted as common knowledge that these glacial cycles are in some way forced by variations in the Earth’s orbit. In particular many have argued that the approximate 100 kyr period of glacial cycles corresponds to variations in the Earth’s eccentricity. As we saw in Professor Baez’s earlier posts, while the variation of eccentricity does affect the total insolation arriving to Earth, this variation is small. Thus many have proposed the existence of a nonlinear mechanism by which such small variations become amplified enough to drive the glacial cycles. Others have proposed that eccentricity is not primarily responsible for the 100 kyr period of the glacial cycles.
Here is a brief summary of some time series analysis I performed in order to better understand the relationship between the Earth’s Ice Ages and the Milankovich cycles.
I used publicly available data on the Earth’s orbital parameters computed by André Berger (see below for all references). This data includes an estimate of the insolation derived from these parameters, which is plotted below against the Earth’s temperature, as estimated using deuterium concentrations in an ice core from a site in the Antarctic called EPICA Dome C:
As you can see, it’s a complicated mess, even when you click to enlarge it! However, I’m going to focus on the orbital parameters themselves, which behave more simply. Below you can see graphs of three important parameters:
• obliquity (tilt of the Earth’s axis),
• precession (direction the tilted axis is pointing),
• eccentricity (how much the Earth’s orbit deviates from being circular).
You can click on any of the graphs here to enlarge them:
Richard Muller and Gordon MacDonald have argued that another astronomical parameter is important: the angle between the plane Earth’s orbit and the ‘invariant plane’ of the solar system. This invariant plane of the solar system depends on the angular momenta of the planets, but roughly coincides with the plane of Jupiter’s orbit, from what I understand. Here is a plot of the orbital plane inclination for the past 800 kyr:
One can see from these plots, or from some spectral analysis, that the main periodicities of the orbital parameters are:
• Obliquity ~ 42 kyr
• Precession ~ 21 kyr
• Eccentricity ~100 kyr
• Orbital plane ~ 100 kyr
Of course the curves clearly are not simple sine waves with those frequencies. Fourier transforms give information regarding the relative power of different frequencies occurring in a time series, but there is no information left regarding the time dependence of these frequencies as the time dependence is integrated out in the Fourier transform.
The Gabor transform is a generalization of the Fourier transform, sometimes referred to as the ‘windowed’ Fourier transform. For the Fourier transform:
one may think of , the ‘kernel function’, as the guy acting as your basis element in both spaces. For the Gabor transform instead of
one defines a family of functions,
where is called the window function. Typical windows are square windows and triangular (Bartlett) windows, but the most common is the Gaussian:
which is used in the analysis below. The Gabor transform of a function is then given by
Note the output of a Gabor transform, like the Fourier transform, is a complex function. The modulus of this function indicates the strength of a particular frequency in the signal, while the phase carries information about the… well, phase.
For example the modulus of the Gabor transform of
is shown below. For these I used the package Rwave, originally written in S by Rene Carmona and Bruno Torresani; R port by Brandon Whitcher.
You can see that the line centered at a frequency of .01 corresponds to the function’s period of 100 time units.
A Fourier transform would do okay for such a function, but consider now a sine wave whose frequency increases linearly. As you can see below, the Gabor transform of such a function shows the linear increase of frequency with time:
The window parameter in both of the above Gabor transforms is 100 time units. Adjusting this parameter effects the vertical blurriness of the Gabor transform. For example here is the same plot as a above, but with window parameters of 300, 200, 100, and 50 time units:
You can see as you make the window smaller the line gets sharper, but only to a point. When the window becomes approximately smaller than a given period of the signal the line starts to blur again. This makes sense, because you can’t know the frequency of a signal precisely at a precise moment in time… just like you can’t precisely know both the momentum and position of a particle in quantum mechanics! The math is related, in fact.
Now let’s look at the Earth’s temperature over the past 800 kyr, estimated from the EPICA ice core deuterium concentrations:
When you look at this, first you notice spikes occurring about every 100 kyr. You can also see that the last 5 of these spikes appear to be bigger and more dramatic than the ones occurring before 500 kyr ago. Roughly speaking, each of these spikes corresponds to rapid warming of the Earth, after which occurs slightly less rapid cooling, and then a slow decrease in temperature until the next spike occurs. These are the Earth’s glacial cycles.
At the bottom of the curve, where the temperature is about about 4 °C cooler than the mean of this curve, glaciers are forming and extending down across the northern hemisphere. The relatively warm periods on the top of the spikes, about 10 °C hotter than the glacial periods. are called the interglacials. You can see that we are currently in the middle of an interglacial, so the Earth is relatively warm compared to rest of the glacial cycles.
Now we’ll take a look at the windowed Fourier transform, or the Gabor transform, of this data. The window size for these plots is 300 kyr.
Zooming in a bit, one can see a few interesting features in this plot:
We see one line at a frequency of about .024, with a sampling rate of 1 kyr, corresponds to a period of about 42 kyr, close to the period of obliquity. We also see a few things going on around a frequency of .01, corresponding to a 100 kyr period.
The band at .024 appears to be relatively horizontal, indicating an approximately constant frequency. Around the 100 kyr periods there is more going on. At a slightly higher frequency, about .015, there appears to be a band of slowly increasing frequency. Also, around .01 it’s hard to say what is really going on. It is possible that we see a combination of two frequency elements, one increasing, one decreasing, but almost symmetric. This may just be an artifact of the Gabor transform or the window and frequency parameters.
The window size for the plots below is slightly smaller, about 250 kyr. If we put the temperature and obliquity Gabor Transforms side by side, we see this:
It’s clear the lines at .024 line up pretty well.
Doing the same with eccentricity:
Eccentricity does not line up well with temperature in this exercise though both have bright bands above and below .01 .
Now for temperature and orbital inclination:
One sees that the frequencies line up better for this than for eccentricity, but one has to keep in mind that there is a nonlinear transformation performed on the ‘raw’ orbital plane data to project this down into the ‘invariant plane’ of the solar system. While this is physically motivated, it surely nudges the spectrum.
The temperature data clearly has a component with a period of approximately 42 kyr, matching well with obliquity. If you tilt your head a bit you can also see an indication of a fainter response at a frequency a bit above .04, corresponding roughly to period just below 25 kyrs, close to that of precession.
As far as the 100 kyr period goes, which is the periodicity of the glacial cycles, this analysis confirms much of what is known, namely that we can’t say for sure. Eccentricity seems to line up well with a periodicity of approximately 100 kyr, but on closer inspection there seems to be some discrepancies if you try to understand the glacial cycles as being forced by variations in eccentricity. The orbital plane inclination has a more similar Gabor transform modulus than does eccentricity.
A good next step would be to look the relative phases of the orbital parameters versus the temperature, but that’s all for now.
If you have any questions or comments or suggestions, please let me know!
References
The orbital data used above is due to André Berger et al and can be obtained here:
• Orbital variations and insolation database, NOAA/NCDC/WDC Paleoclimatology.
The temperature proxy is due to J. Jouzel et al, and it’s based on changes in deuterium concentrations from the EPICA Antarctic ice core dating back over 800 kyr. This data can be found here:
• EPICA Dome C – 800 kyr deuterium data and temperature estimates, NOAA Paleoclimatology.
Here are the papers by Muller and Macdonald that I mentioned:
• Richard Muller and Gordan MacDonald, Glacial cycles and astronomical forcing, Science 277 (1997), 215–218.
• Richard Muller and Gordan MacDonald, Spectrum of 100-kyr glacial cycle: orbital inclination, not eccentricity, PNAS 1997, 8329–8334.
They also have a book:
• Richard Muller and Gordan MacDonald, Ice Ages and Astronomical Causes, Springer, Berlin, 2002.
You can also get files of the data I used here:
• Berger et al orbital parameter data, with explanatory text here.
• Jouzel et al EPICA Dome C temperature data, with explanatory text here.


















Interesting article and nice graphs.
One other thing I would love to see is how changing the window size affects the temperature transform. For example it would be great if you could make an animation showing temperature transform graph while varying the window size from say 800ky to 20ky or so.
Another thing that I would like to know more about is the reliability of the starting temperature record, for one why are there no error bars? How many ice cores is it based on? How much reconstructions from different sites differ?
The temperature data Blake was using coming from a single ice core, called EPICA Dome C. The actual measured data not temperature but the concentration of deuterium in the ice. The scientists claim their work gives a
If you click the link you’ll see the deuterium concentration varies between 370 and 450 parts per thousand. And they seem to be measuring it to an accuracy of roughly 0.5 parts per thousand—that’s what ‰ means.
However, I don’t know what the term ‘optimal accuracy’ means! Accuracy at most this? That would not be very helpful.
Luckily, there are plenty of ice cores, so we can compare the deuterium concentration in one to the deuterium concentration of others. Someone must already be doing this, so there must be papers to read about this.
The much more tricky question is how accurately we can estimate the temperature from the deuterium concentration. I guess the only way we can check these estimates, except for the recent past, is by 1) thinking hard about the physical processes involved and 2) comparing these estimates to estimates done using other methods. So, this is probably one of those stories where scientists slowly bootstrap their way to the truth by a long and complicated line of work. There must be tons of papers about this too, but I bet it takes quite a while to reach the level of expertise needed to understand them, much less assess them.
I tried to win an Innocentive challenge similar to your study, some time ago, and I tried a different method.
The differential equations are the optimal approximator: the solution of a differential equation are the general mathematical series, so why you must use the series (Fourier, Taylor or Laplace) instead to use the differential equation (point of view of mathematical physics)?
The differential equation is complex to obtain for discrete data, so I tried a Not-Linear Prediction Code, that mixed (in your case) the inputs (obliquity,precession and eccentricity) and output (insolation).
When you obtain the right discrete differential equation, then you can try to write the continuous differential equation: in this case you must approximate a continuous differential equation, with free parameters, with the discrete differential equation; so the optimal solution can be write in the continuous equation (you can use the optimal parameter obtained minimizing with L-BFGS, in the original differential equation).
Saluti
Domenico
Hi Domenico,
Sounds interesting, but I’m not sure I understand entirely what you tried to do. Did you try to find a discrete non-linear differential equation for insolation with obliquity, precession, and eccentricity as the independent variables? How did that work? I was under the impression that the insolation is calculated from those parameters, using a particular formula, so maybe you meant temperature as the output?
Thanks for your comment.
I tried to make solar broadcasting for an Innocentive challenge, but it is not simple to download nasa satellite data (there is not a standard, and it is not a perfect open data, and this is a pity).
I tried to obtain differential equations from artificial data (data obtained from computer real function): my idea is that I can give the differential equations from a real functions.
The differential equation are surface in the derivative space, then I think that chaotic data cover better the differential surface; the solution is not unique: the derivative of a differential equation is a solution, and the multiplication for an arbitrary function is a solution; the solution of an arbitrary differential equation is unique.
I search to solve the equation
I can send you my Gnu Public License (free and public) C program, and challenge solution, that I wrote some time ago (if you are interested).
Saluti
Domenico
I think that the right N-Linear Prediction Code must use temperature like output.
The influence of the insolation over the temperature is complex (change of the Earth meteorology), and the solar cycle is complex.
I think that a right equation can incorporate all the effect (for example using the correlation from obliquity, precession, eccentricity and orbital plane to obtain the solar cycle emission).
I think that can be possible to use the derivative of the orbital parameters, so that can be possible to obtain the real differential equation. It is more simple to optimize:
the constant parameters of the differential equation contain implicitly all the variables of the system: this is a universal approximation (it contains all the possible series).
The solution of the differential equation can give the temperature in the years, and it can be possible the future extrapolation (I have never done); the parameters of the equation are lesser of a N- Linear Prediction Code, but it is complex to obtain derivative of real discrete data. If the temperature data is separated in a training set, then it is possible to verify the model on a test set.
Saluti
Domenico
I check the program, and there is an error (excuse me: I have changed the order of a nested for(…), to calculate the derivative of order j).
The differential equation for insolation is:
the differential equation for temperature is:
only the use of L-BFGS permit the error minimization in a short time. ; if the trajectory cover a surface (for example a plane, a cylinder), then the surface is the differential equation.
; if the trajectory cover a surface (for example a plane, a cylinder), then the surface is the differential equation.
It is not necessary, sometime, the minimization of the error function: it is possible to visualize the trajectory in the derivative space
Saluti
Domenico
I tried to solve, in these days, the temperature dynamic with differential equation; and I obtain strange results: I need some days to control programm and results.
I search the differential equation with only the temperature. I start (I stay ever simple, slow and robust, for start) with derivative
with differential equation
and
If I use this definition, then I can change the order, and degree, of the differential equation with command line.
I see that the acceleration of the temperature change with the time, that is lower in old time, and in the current time is higher (human cause? Atmospheric change for microbiological cause?)
The differential equation is (it must be verified):
This is only a joke, because the temperature variation is not continuous (so that is not correct to use the derivative), but this differential equation can be view like a discrete equation (with the variable ).
).
I am sure that can be write a non-linear discrete equation
but I don’t know if it is possible a solution in the time, and the data have not the form
The discrete solution can obtained using a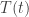 series function, with some free parameter, and minimizing the
series function, with some free parameter, and minimizing the  equation, with the solution in the discrete time.
equation, with the solution in the discrete time.
I think that can be possible a interpolation of the temperature, in equal intervals, using the sparse data.
Saluti
Domenico
I tried some program changes.
![T^{(i)}_n=\frac{1}{2}\left[\frac[T^{(i-1)}_{n+1}-T^{(i-1)_n}{t_{n+1}-t_n}+\frac[T^{(i-1)}_n-T^{(i-1)_{n-1}}{t_n-t_{n-1}}\right]](https://s0.wp.com/latex.php?latex=T%5E%7B%28i%29%7D_n%3D%5Cfrac%7B1%7D%7B2%7D%5Cleft%5B%5Cfrac%5BT%5E%7B%28i-1%29%7D_%7Bn%2B1%7D-T%5E%7B%28i-1%29_n%7D%7Bt_%7Bn%2B1%7D-t_n%7D%2B%5Cfrac%5BT%5E%7B%28i-1%29%7D_n-T%5E%7B%28i-1%29_%7Bn-1%7D%7D%7Bt_n-t_%7Bn-1%7D%7D%5Cright%5D&bg=ffffff&fg=333333&s=0&c=20201002)
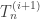 .
.

 is equal to error
is equal to error 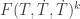 ; so that the strategy is to try all the differential equation with order, and degree, growing; until I obtain a drastic reduction of the error (this is the likely solution, not certain).
; so that the strategy is to try all the differential equation with order, and degree, growing; until I obtain a drastic reduction of the error (this is the likely solution, not certain).

![I(t kyears)=440.41+A\ e^{-0.00436839 t} cos[0.233573 t]+B\ e^{-0.00204178 t} cos(0.315336 t)+C\ e^{-0.00436839 t} sin(0.233573 t)+D\ e^{-0.00204178 t} sin(0.315336 t)](https://s0.wp.com/latex.php?latex=I%28t+kyears%29%3D440.41%2BA%5C+e%5E%7B-0.00436839+t%7D+cos%5B0.233573+t%5D%2BB%5C+e%5E%7B-0.00204178+t%7D+cos%280.315336+t%29%2BC%5C+e%5E%7B-0.00436839+t%7D+sin%280.233573+t%29%2BD%5C+e%5E%7B-0.00204178+t%7D+sin%280.315336+t%29&bg=ffffff&fg=333333&s=0&c=20201002)
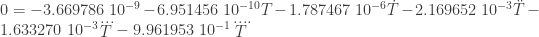

I improved the calculation of the derivatives:
the error is of the order of
I modified the error function of the differential equation (D is the degree):
with this definition the error
With this program I got these two differential equation (5 minutes for each program, with degree, and order, less of 4)
data insolation are correct (the data function is continuous), while the graph of the temperature is not continuous.
I share everithing (as always), even these partial results; they may be interesting to others (that can make better).
Saluti
Domenico
I increase the derivative precision of the derivative (with iteration for higher degree):
with these definition, and with an optimization of the program velocity (more step in the same time) I obtain (this is not the absolute minimum, but the first minimum: there is a little difference):
I verify, with Mathematica, a solution that grow exponentially in the range of the time negative (for insolation).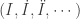 ; so that the trajectory is limited trajectory on the surface.
; so that the trajectory is limited trajectory on the surface.
This happen because the differential equation is linear.
The geometric solution of the differential equation is limited in derivative, and value (the warming and cooling of the Earth cannot be infinite); this can happen if the solution is a closed surface in the derivativ space
If this is true, then must happen three connected surface: normal temperature surface, glacial period and global warming.
I think that the transition from normal temperature to glaciation can be studied in old data, to understand the geometry of the transition.
Saluti
DOmenico
Hi Blake,
I´d love to hear how you produced the code! I am a math kid not really a programmer. But Gabor transforms look really cool. But then I LOVE transforms.
Most of the hard work was done by Rene Carmona, Bruno Torresani, and Wen L. Hwang, who wrote the package Rwave (R is a free programming language commonly used in statistics). The package has implementations of Gabor transforms, continuous and discrete wavelet transforms, all kinds of fun stuff. Their accompanying book is also very helpful, Practical Time-Frequency Analysis by Carmona, Torresani, and Hwang.
Hi Blake. I enjoyed the post. But Garbor transforms are new to me, so I have a couple of questions about what it is you’re actually plotting in those pretty Rwave plots. So, I’ll tell you my guesses and, if you would, please correct me if they’re wrong.
So, using your notation, it looks to me like you have on the vertical axis (labeled frequency),
on the vertical axis (labeled frequency),  on the horizontal axis (labeled time), and
on the horizontal axis (labeled time), and  using some false color scale for the magnitudes. So, far so good?
using some false color scale for the magnitudes. So, far so good?
Now, the thing I’m most puzzled by is the thing with time units you’re calling the “window”. You said your window function in the Garbor transform was a Gaussian , so I’m guessing the window is the standard deviation
, so I’m guessing the window is the standard deviation  ?
?
Is that right? Thanks in advance. And I’m looking forward to the next post.
Hi Dan,
Yep, your guesses are right on. For the Gaussian window,
in the implementation I used the window parameter is so it’s the standard deviation squared, or the variance.
so it’s the standard deviation squared, or the variance.
Thanks for your comment.
Thanks. So, does that mean when you say a plot was done with a window parameter of 300 time units, say, you really mean time units squared? Or are you converting to standard deviations before reporting, so that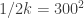 ?
?
Hi Dan,
I mean 300 time units. Sorry I took so long to reply, I had to dig up the C functions that the R library, Rwave, actually calls to make sure.
Hi Blake, nice post !
Do you have a file with the eccentricity, obliquity, precession, inclination, and temperature data ? I’d like to try a couple of things myself …
That data is all available at the links provided in the References of this blog article, but Blake probably has created a more nicely formatted file with that data… and if he emails it to me, I’ll put it on my website and give everyone a link here.
Nice, thanks! A matrix where each rows contains the five values at a given time would be great, but i’ll take any format.
The data is now available on my website. You can reach it by looking at the the References section at the bottom of Blake’s post.
If you have any questions, Giampiero, please ask! And if you succeed in doing any interesting analysis of this data, let us know! You can’t post pictures in comments to this blog, but if you post a link to a picture I can turn it into a picture. Or, you could even write a blog article here if you want.
Thanks, I got the data and performed some (mostly linear) system identification to see if you could find a linear differential equation that could approximate well temperature when the other 4 data are given as inputs (forcing terms in the equation).
The very preliminary answers seems to be “not really”, as the best system somehow reproduces the temperature baseline of the validation data (from obliquity and eccentricity alone) but is not able to really reproduce the peaks:
So it certainly looks like nonlinearity (if not even other input variables) does play an important role in the final temperature history. I might try something more on the nonlinear identification front in the next few weeks.
Have people been successful in devising a model capable of reproducing past temperature successfully? And how successfully?
That graph of yours is very interesting, Giampiero! The colored curve does match some important features of the observed temperature (as estimated from deuterium concentration), but it clearly misses the big peaks.
I’m not an expert on these attempts… I should become one!
For now, I recommend that you look at the very simple model of Didier Paillard, discussed in Part 10 of my ‘Mathematics of the Environment’ course. This is highly nonlinear qualitative model where the Earth has just 3 states, and it changes state according to certain rules involving the insolation (a quantity computed from the orbital parameters). But if you read his paper—which I will send you—you’ll see he has a similar more detailed quantitative model.
I’m not saying this is the only model or the best one. It’s the one I happen to know.
Interesting, thanks. So I have read the whole “math of the environment” series, including part 10, and then the article that you sent me. Here are a few sparse thoughts:
I would not say that the qualitative model has “3 states” (e.g. as in 3 different dimensions like position and velocity), but just one state and 3 different allowed values (regimes or modes) along that dimension (that is i, g and G). This is just a language issue but i thought it’s better to state it clearly to avoid misunderstanding as to what a state means to different people.
One thing that would be interesting to add to this post would be the Gabor transform of the insolation, to see how it compares to obliquity, eccentricity and temperature. My guess is that it should contain frequencies of both obliquity and eccentricity and overlap well with temperature.
Having the insolation data, i could rerun the identification to see if i can reproduce the results in the graph from insolation alone, as the paper suggest it might be possible. Yes i have seen the insolation page on Azimuth, but i wish there was a formula that i could directly apply to the data.
I like very much the quantitative 2-state model in Paillard’s paper, i wish he had described better (with an actual formula) the switching between i,g,and G modes. However that model describes the ice volume, not the temperature, so i wonder if one can assume a direct proportional (or probably affine) relationship between ice volume and temperature. If so it could be straightforward to see what kind of fitting you could do by adjusting that parameter.
One final comment is that it looks as if he used the whole data for 800KYrs to fit the model, and then validated the model using the same exact data, which is not the best of practices. It is true that since the model is very small that shouldn’t be a big issue, but nevertheless i am left wondering, especially given the results of Fig4, where it looks like he played with radiative forcing as well.
Giampiero wrote:
I should give you a more substantial reply, but I’m in a rush, and trivial issues of language are fun to argue about, so I’ll only do that.
In physics, the state of a system is a complete description of the way it is at some given time. For example, if we have a particle on a line with position 3 and velocity -7, its state is (3,-7). In traditional physics there’s usually an infinite set of states, since the set of real numbers is infinite. But there are also systems with finitely many states, and computer science gives many examples, called ‘finite-state machines’.
In physics, if we describe the state of a system by a list of n numbers, we say the system has n degrees of freedom.
So, I was trying to say that Paillard’s model has 3 different states: i, g, and G, together with certain rules for hopping between these states.
This is perhaps oversimplified since these rules involve how long the system has been in the g (mild glacial) state. So, one can argue that the amount of time spent in the mild glacial state should also be counted as part of the description of that state. Doing this makes sense because he essentially assumes that ice builds up linearly with time in this state, if the insolation stays low enough. So, the amount of time is a proxy for the amount of ice.
If you have the time and desire to do any more calculations or modelling, please let me know, and I’ll be glad to help out: I like to think and I don’t like to program!
I really liked your ‘best linear prediction’ here:
and I would like to know exactly how it’s defined. I think we could have fun quantitatively measuring the amount of nonlinearity of the Earth’s climate system, and I have some ideas for how to do that.
John wrote:
Yes, assuming at least that the system is autonomous (no input), I am very comfortable with this definition, and perhaps it’s the best way to define the state even when the system has inputs.
Traditionally in control engineering too the cardinality of the set of possible states is infinity (yes, i know, technically aleph … something), and so we informally (and incorrectly) refer to the “number of states” as the number of variables that are needed to define the state of a system. I guess that “degrees of freedom” could be confusing when talking to mechanical engineers since a mechanical system that is said to have, for example, 2 DOF, needs a vector of 4 numbers (2 positions and 2 velocities) to represent its state.
That was a model identified with an ARMAX structure (see this and this). Very roughly speaking this is a discrete-time transfer function with some filtered additive noise. The transfer function (TF) has 2 poles, 2 zeros, and another zero that serves as a pure delay (this TF can be converted into a state space discrete-time model with 1 output, 2 inputs and 2 “degrees of freedom”). The noise filter also has 2 zeros (and the same 2 poles of the TF).
I am sorry if this is incomprehensible, but right now i can’t say much more, i’ll try to say more later if you are interested.
This looks really interesting, I wonder how you would do it, maybe just subtracting the outputs of the linear and nonlinear model and have a look at its energy.
Perhaps I can try to do something just once in a while. I think that however the first step would be to agree on which input to use (just insolation, obliquity, eccentricity, or maybe all of the above?) and which output to measure (temperature or ice volume). Otherwise I don’t think we can make an apple to apple comparison.
By the way the structure of the ARMAX model is here:
where is the temperature,
is the temperature,  is a vector containing obliquity and eccentricity,
is a vector containing obliquity and eccentricity,  is white noise.
is white noise.
Giampiero,
the missed peaks in your graph remind me of a Kalman filter I used at work to predict electricity load: It was very bad at predicting the daily peak.
Alas that job is gone and I haven’t gone any deep into time series stochastics stuff (some gargantuan Excel wizardry turned out sufficient to significantly improve prognosis). And before the job I never felt interested – which I regret now. Any book recommendation beyond A.N. Shiryaev’s Probability book?
Autoregressive models smell a bit oversimplifying to me – but that’s probably because I didn’t get the knack yet. My intuition (possibly wrong) is: ARMAX is a sort of “small” Kalman filter.
Florifulgurator,
in my experience such missing peaks are often one of the telltale signs of unmodeled nonlinear behavior. You should have tried perhaps with an Extended or Ensemble KF, but at the end of the day they are only as good as the (nonlinear) model of the system you have. If your model is not that great, they cannot make miracles.
Regarding your last comment, well, not really. A KF is a filter that you attach to a system in order to observe (reconstruct and filter out the noise) the state of the system at that particular time. It needs to have an internal model of the system to work (as well as access the system’s inputs and outputs).
An ARMAX model is just a model of the system, with no particular purposes rather than trying to reproduce the system’s output given its inputs.
The armax system that i have identified is this (i’ll copy and paste more info here below):
amx2221 =
Discrete-time ARMAX model: A(z)y(t) = B(z)u(t) + C(z)e(t)
A(z) = 1 – 1.873 z^-1 + 0.8778 z^-2
B1(z) = 19.87 z^-1 – 19.91 z^-2
B2(z) = 21.26 z^-1 – 21.68 z^-2
C(z) = 1 – 0.6272 z^-1 – 0.2794 z^-2
Name: amx2221
Sample time: 1 seconds
Parameterization:
Polynomial orders: na=2 nb=[2 2] nc=2 nk=[1 1]
Number of free coefficients: 8
Use “polydata”, “getpvec”, “getcov” for parameters and their uncertainties.
Status:
Estimated using POLYEST on time domain data “0-400-12”.
Fit to estimation data: 79% (prediction focus)
FPE: 0.3427, MSE: 0.3291
It is very simple indeed, just a few parameters, but often simple things work better and are anyway more useful than complicated ones. Indeed this outperforms more complicated systems.
Don’t try to read into these equations too much, stuff like “A(z)y(t)” is really a shorthand notation for convolution not a multiplication. And the sample time is not really one second (which is the default one) but one Kyear (this would matter when converting the model to a continuous-time one).
These Garbor transform graphs are great, and the evidence for obliquity and some combination of inclination and eccentricity as drivers of temperature seems convincing. (If one didn’t know Newton’s laws, one could conversely conclude that temperature changes were driving changes in the earth’s orbital parameters, which would make human caused temperature changes much more frightening!)
However, since the variations in the orbital parameters are presumably persistent and not localized in time, why use a time-local transform like the Garbor transform (which was new to me, thanks!) instead of one that samples your entire data set with equal weight? In these plots, I see horizontal lines that vary a little bit in intensity, but no salient features that really appear and disappear over time.
Temperature changes not related to our orbit should suddenly appear and disappear, though. How would the current temperature spike look in a Garbor plot made by scientists millions of years in our future? If the Permian-Triassic extinction event, for example, were caused by the exponential growth in CO2 production by a race of technological squids and the consequent warming, would we be able to see that local event on a Garbor temperature plot extending back 200 million years?
Over long enough time scales, the variations in orbital parameters aren’t constant. Apart from anything else, the Earth-Moon distance is steadily increasing, and the Earth’s spin slowing. This alone would be enough to change the periods of the variations.
On a multi-million year time scale, the sensitivity of climate to orbital parameters also changes, thanks to continental drift. The Arctic may be especially sensitive at the moment, being an almost landlocked sea. The Antarctic, an island continent, may be less sensitive.
Presumably, the Garbor transform filters out such effects.
David Lyon wrote:
Your point is a good one. While there are certain slow changes in the cyclic variations of the Earth’s Milankovitch cycles, these wouldn’t be noticeable over the rather short (800,000-year) time period covered by the EPICA Dome C ice core. So in this post, taking the Gabor transform of the Milankovitch cycles is essentially just a charismatic way to draw their Fourier transform!
The Gabor transform of the temperature, however, has the potential to be more interesting. Over the period covered here, the way it changes with time is very subtle:
But if Blake gets ahold of good data going back over a million years ago, he should be able to study a famous phenomenon: the way the dominant period of the glacial cycle shifted from 41 kyr to 100 kyr about one million years ago!
The most famous data illustrating this is Lisiecki and Raymo’s collection of ocean sediment cores taken from 57 different locations. It gives this graph:
The data is publicly available:
• Lorraine E. Lisiecki and Maureen E. Raymo, A Pliocene-Pleistocene stack of 57 globally distributed benthic δ18O records, Paleoceanography 20 (2005), PA1003. Data available on Lisiecki’s website.
Unfortunately, these authors used Milankovitch cycles to ‘improve’ the dating of their sediment cores! This introduces a kind of circular reasoning if we try to compare their data to Milankovitch cycles.
Right now Blake is trying to get ahold of some data going back over 1 million years that wasn’t ‘improved’ in this way. The Gabor transform of this could be very interesting.
When I was younger, I read many things, many things by Isaac Asimov and my favourite (as well as his favourite) were his essays written for F&SF (which I read as books of 17 issues each). One was on the Milankovich cycles: “Oblique the centric globe”.
The thing to keep in mind here is that Milankovitch cycles have been around for far longer than the current Ice Age glaciations have been around, therefore one cannot assume that Milankovitch cycles are the cause of glaciations. This is a case of confusing correlations with causes — a big no-no in statistics. The other thing is the abuse of the word “average”. It is misleading to say that glaciations, on average, last 100,000 years, therefore Milankovitch cycles must be causing them since it doesn’t address probability distribution. Glaciations typically have lasted either 80,000 years or 120,000 years — and the average of those two numbers is 100,000 years, so just because a correlation exists, even a very good one, doesn’t prove there is any relationship between it and reality. And if you really want to do the math, remember that the change in solar insolation due to Milankovitch cycles isn’t enough to explain the change in temperature during glaciation events. The more rational explanation is that glaciations are synchronized to Milankovitch cycles, not caused by them.
The mechanism linking orbital cycles and the ice ages is simple: solar intensity, which varies with orbital forcing, correlates with the derivative of global ice volume. For details, see Roe G. (2006), “In defense of Milankovitch”, Geophysical Research Letters, 33, L24703; doi:10.1029/2006GL027817.
I published a non-technical explanation of that in the Wall Street Journal (5 April 2011). The article is How scientific is climate science?; see the box entitled “An insupportable assumption”.
This talk presents a lot of what Blake Pollard and I have said about Milankovitch cycles, in a condensed way.
People have lots of tricks for studying ‘signals’, like series of numbers or functions
or functions 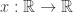 . One method is to ‘transform’ the signal in a way that reveals useful information. The Fourier transform decomposes a signal into sines and cosines of different frequencies. This lets us see how much power the signal has at different frequencies, but it doesn’t reveal how the power at different frequencies changes with time. For that we should use something else, like the Gabor transform explained by Blake Pollard in a previous post.
. One method is to ‘transform’ the signal in a way that reveals useful information. The Fourier transform decomposes a signal into sines and cosines of different frequencies. This lets us see how much power the signal has at different frequencies, but it doesn’t reveal how the power at different frequencies changes with time. For that we should use something else, like the Gabor transform explained by Blake Pollard in a previous post.
Sines and cosines are great, but we might want to look for other patterns in a signal. A ‘continuous wavelet transform’ lets us scan a signal for appearances of a given pattern at different times and also at different time scales: a pattern could go by quickly, or in a stretched out slow way.
[…] Figure 8. Disparity between calculations from Milankovitch theory and data from observations. A Gabor transform is a windowed time-frequency Fourier analysis. When applied to the 65°N summer insolation calculations from the orbit of the Earth during the last 800 kyr it shows the main contributors to that signal thought to be responsible for glacial terminations. The main contributor is the 23 kyr period, followed by the 18 kyr period, both from precession cycles, followed by the less intense 41 kyr period from obliquity cycles. When the same analysis is performed over the temperature data from observations (Epica Dome C ice core record), we can see that the temperature of the Earth barely responds to precession, as the band at 23 kyr is very tenuous. Instead we see obliquity bands at 41 and 83 kyr (double harmonic) and the prominent band at 100 kyr, that cannot be the eccentricity, since it is missing what should be an even stronger band at 413 kyr. Source: John Baez. […]