If you could watch an individual water molecule, once in a while you’d see it do this.
As it bounces around, every so often it hits another water molecule hard enough enough for one to steal a hydrogen nucleus—that is, a proton—from the other!
The water molecule with the missing proton is called a hydroxide ion, OH⁻. The one with an extra proton is called a hydronium ion, H₃O⁺.
This process is called the ‘autoionization’ of water. Thanks to this, a few molecules in a glass of water are actually OH⁻ or H₃O⁺, not the H₂O you expect.
And this gives a cool way for protons to move through water. Here’s a little movie of how it works, made by Mark Petersen:
A positively charged proton gets passed from one molecule to another! This is called the ‘Grotthuss mechanism’, because Theodor Grotthuss proposed this theory in his paper “Theory of decomposition of liquids by electrical currents” back in 1806. It was quite revolutionary at the time, since ions were not well understood.
Something like this theory is true. But in fact, I believe all the pictures I’ve shown so far are oversimplified! A hydronium ion is too powerfully positive to remain a lone H₃O⁺. It usually attracts a bunch of other water molecules by the van der Waals force and creates larger structures. You can see these here:
• Water, Azimuth, 29 November 2013.
Water with even trace amounts of salts in it conducts electricity vastly better than pure water, because when salts dissolve in water they create free ions. So, the Grotthus mechanism seems to be the dominant form of electrical conduction in water only when the water is extremely pure. According to Wikipedia:
Pure water containing no exogenous ions is an excellent electronic insulator, but not even “deionized” water is completely free of ions. Water undergoes autoionization in the liquid state when two water molecules form one hydroxide anion (OH⁻) and one hydronium cation (H₃O⁺). Because of autoionization, at ambient temperatures pure liquid water has a similar intrinsic charge carrier concentration to the semiconductor germanium and an intrinsic charge carrier concentration three orders of magnitude greater than the semiconductor silicon, hence, based on charge carrier concentration, water can not be considered to be a completely dielectric material or electrical insulator but to be a limited conductor of ionic charge.
Because water is such a good solvent, it almost always has some solute dissolved in it, often a salt. If water has even a tiny amount of such an impurity, then the ions can carry charges back and forth, allowing the water to conduct electricity far more readily.
It is known that the theoretical maximum electrical resistivity for water is approximately 18.2 MΩ·cm (182 kΩ·m) at 25 °C. This figure agrees well with what is typically seen on reverse osmosis, ultra-filtered and deionized ultra-pure water systems used, for instance, in semiconductor manufacturing plants. A salt or acid contaminant level exceeding even 100 parts per trillion (ppt) in otherwise ultra-pure water begins to noticeably lower its resistivity by up to several kΩ·m.
I have a couple of questions:
Puzzle 1. What fraction of water molecules are autoionized at any time? It should be possible to compute this for water at 25℃ knowing that
at this temperature.
Puzzle 2. How often, on average, does an individual water molecule autoionize? Wikipedia says it happens about once every 10 hours, and cites this paper:
• Manfred Eigen and L. De Maeyer, Untersuchungen über die Kinetik der Neutralisation I, Z. Elektrochem. 59 (1955), 986.
But I don’t know how this was estimated, so I don’t know how seriously to take it.
If we knew answers to Puzzles 1 and 2, maybe we could compute how long an individual molecule remains ionized each time it autoionizes, on average. But I’m worried about a lot of subtleties that I don’t really understand.
For more, read:
• Wikipedia, Self-ionization of water.
• Wikipedia, Grotthuss mechanism.
Azimuth 
10 hours is a great time scale. One never meets time scales like that in physics. Except for the half-life of a lone neutron (931 sec), only 1.5 orders of magnitude away.
There must be autoionization of water, or pH wouldn’t make sense. The neutral pH of 7 is half the opposite of the common logarithm of that number 1.006×10⁻¹⁴ that you cited. (That this number is close to a power of 10 when measured in square molars is one of those lucky coincidences.)
In principle, the concentration of hydronium ions is 10⁻⁷ moles per litre, a litre of water weighs 1000 grams (this one is not a coincidence), and a mole of water weighs 2×1+1×16=18 grams, so the proportion of water molecules that have ionized to hydronium should be 10⁻⁷÷1000×18, so about 1.8 parts per billion. Another 1.8 parts per billion should be hydroxide ions. But as you noted, hydronium attracts additional water molecules, which complicates the calculation for Puzzle 1.
I think that’s the answer I was looking for: 1.8 in a billion water molecules are hydronium and 1.8 in a billion are hydroxide at 25 Celsius… ignoring the fact that either of these ions are really part of a larger structure involving multiple water molecules. Thanks!
It’s what I remember best from high-school chemistry class: dimensionalysis!
Puzzle 1 is mostly a change in units.
At pH=7 (neutral for water) the concentration of hydroxide and hydronium are equal,
.
and that there are two species that are charged, this is about 
ionized water molecules in your nalgene bottle. (pH=7 is probably what we should use; dissolving other stuff in the water would shift the pH higher or lower but we don’t care about other stuff, we care about water. :)
[OH–]=[H3O+]=
So, recalling Avogadro’s number
For Puzzle 2… I’ll make a stab with some dimensional analysis, which will give us some context at least.
First. I don’t think “auto-ionize” is a great term. The proton is being exchanged with *another water molecule*; it has help. So let’s model that interaction.
To estimate encounter rates, we’ll use the volume per second swept out by a water molecule of area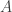
and speed 
and multiply by the concentration [OH–] of hydroxide, that should give us how many mol of hydroxide per sec a single molecule of water “hits”.
• Looking up OH-bond length and oxygen diameter (each
Å) and using the angle of 104° gives us an area of roughly 
, and Googling seems to bear out numbers in that range.
• [OH^-]
as per puzzle 1, recalling 
• For
let’s use the equipartition theorem from thermo; each energy mode has about 
of energy at equilibrium, so 
gives us something like 
. (This is *extremely* rough, water is *not* an ideal gas! If we get numbers that make no sense this should be revisited first.)
Assuming my arithmetic isn’t badly wrong,
— so about a thousand hits a second for our intrepid little water molecule! If the once per 10 hour rule is to be believed, that is a conversion efficiency of one reaction per 10 million collisions, roughly. I’ll ask a physical chemist friend of mine if he has any intuition on these kinds of conversion rates. I expect that is extremely high for almost any other substance in the absence of catalyst, but maybe someone else knows something to help us triangulate.
Further bloviation:
To know how many hits *should* result in a proton-exchange from first principles would require computing the gibbs free energy
of the transition complex HO-H-OH2. This might actually be the kind of thing you could estimate with molecular orbitals, if you have a friendly physical chemist and a free computer lying around.
The problem, is that water is weird; it shouldn’t even be a liquid at STP when compared to other molecules, but *exactly this kind of temporary H-bonding* is believed to collectively yield the observed facts that water is an unusually “sticky” substance and a very powerful solvent. So its very likely that the transition complex is substantially stabilized by all the water around it. One effect of this is observed in the bulk and can be calculated theoretically; in water the usual
Coulomb-potential is “screened” to be a Debye potential 
, which has radically different properties when you calculate moments etc. This is why charged species can even exist in solution at all — the Coulomb force being the strongest of the fundamental forces we encounter in ordinary matter.
Anyway, hopefully someone else knows something that can help us triangulate the above conversion efficiency.
By chance I was watching a health-related video and at about 8.41 it starts talking about a peculiar property of water which is relevant to heart health: https://youtu.be/MLBmO5LJqmA?t=521. Basically, near a hydrophilic surface the negative ions like to be close to it. I also recommend the video’s pro-sun message.
Oh excuse me, I was modelling proton exchange and you asked about “auto-ionization” e.g. two water molecules cross-ionizing to hydroxide and hydronium… I was implicitly assuming that auto-ionization is *much* rarer than proton-exchange on a per collision basis and was trying to use the latter as an upper bound. I never said that though, so what I wrote is probably confusing.
I do wonder if autoionisation loop is possible. Looking at the second gif, I keep wondering a very unphysical question — if we put 6 of the molecules in a hexagon, 5 normal h2o and one ion h3o+, can they keep passing each other the lone proton?
They could in theory do that, but it’s something that would happen with very low probability. It would be a perpetual motion machine of the sort that violates thermodynamic laws if the proton were to move around the hexagon clockwise more often than it moves counterclockwise.
As much as I remember from my chemistry studies the Grotthuss mechanism is essentially quantum tunneling in action. So shouldn’t there be a first principle way to study it, solely based on the wavefunction of the hydrogen atom? Also I remember from biochemistry that the proton channel molecules in the cell’s or some organelle’s membranes consist of a prearranged chain of water molecules filling the pore. So protons do not move physically through the pores, but by the Grotthuss mechanism involving a chain of tunneling events. To my understanding this happens way faster than any diffusion would do. Since proton gradients are terribly important for ATP production, one could say, that tunneling facilitates the existence of life as we know it (of course, I guess without the possibility of quantum tunneling, there also would be a different way of fusion and nucleosynthesis in stars, but I don’t remember these details too much).
Biochemical applications of the Grotthuss mechanism would be really cool to understand, but maybe also complex—I don’t know how much the pore itself, and ions dissolved in the water, affect things. Someone must have studied this already.
The Grotthuss mechanism should be easier to study with ab initio calculations in the case of pure water… but it may still be complex, since it involves interactions between at least two water molecules, and the probability density of the distance between two water molecules depends on interactions between many water molecules: computing it accurately is famously difficult, since it requires understanding the complex patterns that molecules tend to form in liquid water. (For pictures of these patterns, try this.) But if one just wants rough answers, it may be not so bad.