Cold-Resistant Trees

The Appalachians are an old, worn-down mountain chain that runs down the eastern side of North America. The ecology of the Appalachians is fascinating. For example:

Ecologists have tested many species of Appalachian trees to see how much cold they can survive. As you’d expect, for many trees the killing temperature is just a bit colder than the lowest temperatures at the northern end of their range. That makes sense: presumably they’ve spread as far north—and as far up the mountains—as they can.

But some other trees can survive temperatures much lower than that! For example white and black spruce, aspen and balsam poplar can survive temperatures of -60° C, which is -80° F. Why is that?

One guess is that this extra hardiness is left over from the last glacial cycle, which peaked 20,000 years ago—or even previous glacial cycles. It got a lot colder then!

So, maybe these trees are native to the northern Appalachians—while others, even those occupying the same regions, have only spread there since it warmed up around 10,000 years ago. Ancient pollen shows that trees have been moving north and south with every glacial cycle.

I learned about this issue here:

• Scott Weidensaul, Mountains of the Heart: a Natural History of the Appalachians, Fulcrum Publishing, 2016.

I bought this book before a drive through the Appalachians.

To add some extra complexity to the story, David C. writes:

I’d love to understand more and reconcile that with the fact that none of these trees do well above around 4500 ft in the northern Appalachians (New Hampshire).

and Brian Hawthorne writes:

Don’t forget that all the tree species had to move back into the areas that were under the last glacier.

Anthocyanins

 

As the chlorophyll wanes, now is the heyday of the xanthophylls,
carotenoids and anthocyanins. These contain carbon rings and chains whose electrons become delocalized… their wavefunctions resonating at different frequencies, emitting photons of yellow, orange and red!

Yes, it’s fall. I’m enjoying it.

I wrote about two xanthophylls in my May 27, 2014 diary entry: I explained how they get their color from the resonance of delocalized electrons that spread all over a carbon chain with alternating single and double bonds:

I discussed chlorophyll, which also has such a chain, in my May 29th entry. I wrote about some carotenoids in my July 2, 2006 entry: these too have long chains of carbons with alternating single and double bonds.

I haven’t discussed anthocyanins yet! These have rings rather than chains of carbon, but the basic mechanism is similar: it’s the delocalization of electrons that makes them able to resonate at frequencies in the visual range. They are often blue or purple, but they contribute to the color of many red leaves:

Click on these two graphics for more details! I got them from a website called Science Notes, and it says:

Some leaves make flavonoids. Anthocyanins are flavonoids which vary in color depending on pH. Anthocyanins are not usually present in leaves during the growing season. Instead, plants produce them as temperatures drop. They acts as a natural sunscreen and protect against cold damage. Anthocyanins also deter some insects that like to overwinter on plants and discourage new seedlings from sprouting too close to the parent plant. Plants need energy from light to make anthocyanins. So, vivid red and purple fall colors only appear if there are several sunny autumn days in a row.

This raises a lot of questions, like: how do anthocyanins protect
leaves from cold, and why do some leaves make them only shortly before they die? Or are they there all along, hidden behind the chlorophyll Maybe this paper would help:

• D. Lee and K. Gould, Anthocyanins in leaves and other vegetative organs: an introduction, Advances in Botanical Research 37 (2002), 1–16.

Thinking about anthocyanins has led me to ponder the mystery of aromaticity. Roughly, a compound is aromatic if it contains one or more rings with pi electrons delocalized over the whole ring. But people fight over the exact definition.

I may write more about this if I ever solve some puzzles that are bothering me, like the mathematical origin of Hückel’s rule, which says a planar ring of carbon atoms is aromatic if it has pi electrons. I want to know where the formula comes from, and I’m getting close.

An early paper by Linus Pauling discusses the resonance of electrons in anthocyanins and other compounds with rings of carbon. This one is freely available, and it’s pretty easy to read:

• Linus Pauling, Recent work on the configuration and electronic structure of molecules; with some applications to natural products, in Fortschritte der Chemie Organischer Naturstoffe, 1939, Springer, Vienna, pp. 203–235.

Nonequilibrium Thermodynamics in Biology

William Cannon and I are organizing a special session on thermodynamics in biology at the American Physical Society March Meeting, which will be held in Chicago on March 14–18, 2022.

If you work on this, please submit an abstract here before October 22! Our session number is 03.01.32.

Non-equilibrium Thermodynamics in Biology: from Chemical Reaction Networks to Natural Selection

Since Lotka, physical scientists have argued that living things belong to a class of complex and orderly systems that exist not despite the second law of thermodynamics, but because of it. Life and evolution, through natural selection of dissipative structures, are based on non-equilibrium thermodynamics. The challenge is to develop an understanding of what the respective physical laws can tell us about flows of energy and matter in living systems, and about growth, death and selection. This session will address current challenges including understanding emergence, regulation and control across scales, and entropy production, from metabolism in microbes to evolving ecosystems.

We have some speakers lined up already. Eric Smith of the Santa Fe Institute will speak on “Combinatorics in evolution: from rule-based systems to the thermodynamics of selectivities”. David Sivak of Simon Fraser University will speak on “”Nonequilibrium energy and information flows in autonomous systems”.

If you have any questions, please ask.

Fisher’s Fundamental Theorem (Part 4)

I wrote a paper that summarizes my work connecting natural selection to information theory:

• John Baez, The fundamental theorem of natural selection.

Check it out! If you have any questions or see any mistakes, please let me know.

Just for fun, here’s the abstract and introduction.

Abstract. Suppose we have n different types of self-replicating entity, with the population of the ith type changing at a rate equal to times the fitness of that type. Suppose the fitness is any continuous function of all the populations . Let be the fraction of replicators that are of the ith type. Then is a time-dependent probability distribution, and we prove that its speed as measured by the Fisher information metric equals the variance in fitness. In rough terms, this says that the speed at which information is updated through natural selection equals the variance in fitness. This result can be seen as a modified version of Fisher’s fundamental theorem of natural selection. We compare it to Fisher’s original result as interpreted by Price, Ewens and Edwards.

Introduction

In 1930, Fisher stated his “fundamental theorem of natural selection” as follows:

The rate of increase in fitness of any organism at any time is equal to its genetic variance in fitness at that time

Some tried to make this statement precise as follows:

The time derivative of the mean fitness of a population equals the variance of its fitness.

But this is only true under very restrictive conditions, so a controversy was ignited.

An interesting resolution was proposed by Price, and later amplified by Ewens and Edwards. We can formalize their idea as follows. Suppose we have n types of self-replicating entity, and idealize the population of the ith type as a real-valued function . Suppose

where the fitness is a differentiable function of the populations of every type of replicator. The mean fitness at time is

where is the fraction of replicators of the ith type:

By the product rule, the rate of change of the mean fitness is the sum of two terms:

The first of these two terms equals the variance of the fitness at time t. We give the easy proof in Theorem 1. Unfortunately, the conceptual significance of this first term is much less clear than that of the total rate of change of mean fitness. Ewens concluded that “the theorem does not provide the substantial biological statement that Fisher claimed”.

But there is another way out, based on an idea Fisher himself introduced in 1922: Fisher information. Fisher information gives rise to a Riemannian metric on the space of probability distributions on a finite set, called the ‘Fisher information metric’—or in the context of evolutionary game theory, the ‘Shahshahani metric’. Using this metric we can define the speed at which a time-dependent probability distribution changes with time. We call this its ‘Fisher speed’. Under just the assumptions already stated, we prove in Theorem 2 that the Fisher speed of the probability distribution

is the variance of the fitness at time t.

As explained by Harper, natural selection can be thought of as a learning process, and studied using ideas from information geometry—that is, the geometry of the space of probability distributions. As changes with time, the rate at which information is updated is closely connected to its Fisher speed. Thus, our revised version of the fundamental theorem of natural selection can be loosely stated as follows:

As a population changes with time, the rate at which information is updated equals the variance of fitness.

The precise statement, with all the hypotheses, is in Theorem 2. But one lesson is this: variance in fitness may not cause ‘progress’ in the sense of increased mean fitness, but it does cause change!

For more details in a user-friendly blog format, read the whole series:

• Part 1: the obscurity of Fisher’s original paper.

• Part 2: a precise statement of Fisher’s fundamental theorem of natural selection, and conditions under which it holds.

• Part 3: a modified version of the fundamental theorem of natural selection, which holds much more generally.

• Part 4: my paper on the fundamental theorem of natural selection.

Nonequilibrium Thermodynamics in Biology (Part 2)

Larry Li, Bill Cannon and I ran a session on non-equilibrium thermodynamics in biology at SMB2021, the annual meeting of the Society for Mathematical Biology. You can see talk slides here!

Here’s the basic idea:

Since Lotka, physical scientists have argued that living things belong to a class of complex and orderly systems that exist not despite the second law of thermodynamics, but because of it. Life and evolution, through natural selection of dissipative structures, are based on non-equilibrium thermodynamics. The challenge is to develop an understanding of what the respective physical laws can tell us about flows of energy and matter in living systems, and about growth, death and selection. This session addresses current challenges including understanding emergence, regulation and control across scales, and entropy production, from metabolism in microbes to evolving ecosystems.

Click on the links to see slides for most of the talks:

• Persistence, permanence, and global stability in reaction network models: some results inspired by thermodynamic principles
Gheorghe Craciun, University of Wisconsin–Madison

The standard mathematical model for the dynamics of concentrations in biochemical networks is called mass-action kinetics. We describe mass-action kinetics and discuss the connection between special classes of mass-action systems (such as detailed balanced and complex balanced systems) and the Boltzmann equation. We also discuss the connection between the ‘global attractor conjecture’ for complex balanced mass-action systems and Boltzmann’s H-theorem. We also describe some implications for biochemical mechanisms that implement noise filtering and cellular homeostasis.

• The principle of maximum caliber of nonequilibria
Ken Dill, Stony Brook University

Maximum Caliber is a principle for inferring pathways and rate distributions of kinetic processes. The structure and foundations of MaxCal are much like those of Maximum Entropy for static distributions. We have explored how MaxCal may serve as a general variational principle for nonequilibrium statistical physics—giving well-known results, such as the Green-Kubo relations, Onsager’s reciprocal relations and Prigogine’s Minimum Entropy Production principle near equilibrium, but is also applicable far from equilibrium. I will also discuss some applications, such as finding reaction coordinates in molecular simulations non-linear dynamics in gene circuits, power-law-tail distributions in ‘social-physics’ networks, and others.

• Nonequilibrium biomolecular information processes
Pierre Gaspard, Université libre de Bruxelles

Nearly 70 years have passed since the discovery of DNA structure and its role in coding genetic information. Yet, the kinetics and thermodynamics of genetic information processing in DNA replication, transcription, and translation remain poorly understood. These template-directed copolymerization processes are running away from equilibrium, being powered by extracellular energy sources. Recent advances show that their kinetic equations can be exactly solved in terms of so-called iterated function systems. Remarkably, iterated function systems can determine the effects of genome sequence on replication errors, up to a million times faster than kinetic Monte Carlo algorithms. With these new methods, fundamental links can be established between molecular information processing and the second law of thermodynamics, shedding a new light on genetic drift, mutations, and evolution.

• Nonequilibrium dynamics of disturbed ecosystems
John Harte, University of California, Berkeley

The Maximum Entropy Theory of Ecology (METE) predicts the shapes of macroecological metrics in relatively static ecosystems, across spatial scales, taxonomic categories, and habitats, using constraints imposed by static state variables. In disturbed ecosystems, however, with time-varying state variables, its predictions often fail. We extend macroecological theory from static to dynamic, by combining the MaxEnt inference procedure with explicit mechanisms governing disturbance. In the static limit, the resulting theory, DynaMETE, reduces to METE but also predicts a new scaling relationship among static state variables. Under disturbances, expressed as shifts in demographic, ontogenic growth, or migration rates, DynaMETE predicts the time trajectories of the state variables as well as the time-varying shapes of macroecological metrics such as the species abundance distribution and the distribution of metabolic rates over
individuals. An iterative procedure for solving the dynamic theory is presented. Characteristic signatures of the deviation from static predictions of macroecological patterns are shown to result from different kinds of disturbance. By combining MaxEnt inference with explicit dynamical mechanisms of disturbance, DynaMETE is a candidate theory of macroecology for ecosystems responding to anthropogenic or natural disturbances.

• Stochastic chemical reaction networks
Supriya Krishnamurthy, Stockholm University

The study of chemical reaction networks (CRN’s) is a very active field. Earlier well-known results (Feinberg Chem. Enc. Sci. 42 2229 (1987), Anderson et al Bull. Math. Biol. 72 1947 (2010)) identify a topological quantity called deficiency, easy to compute for CRNs of any size, which, when exactly equal to zero, leads to a unique factorized (non-equilibrium) steady-state for these networks. No general results exist however for the steady states of non-zero-deficiency networks. In recent work, we show how to write the full moment-hierarchy for any non-zero-deficiency CRN obeying mass-action kinetics, in terms of equations for the factorial moments. Using these, we can recursively predict values for lower moments from higher moments, reversing the procedure usually used to solve moment hierarchies. We show, for non-trivial examples, that in this manner we can predict any moment of interest, for CRN’s with non-zero deficiency and non-factorizable steady states. It is however an open question how scalable these techniques are for large networks.

• Heat flows adjust local ion concentrations in favor of prebiotic chemistry
Christof Mast, Ludwig-Maximilians-Universität München

Prebiotic reactions often require certain initial concentrations of ions. For example, the activity of RNA enzymes requires a lot of divalent magnesium salt, whereas too much monovalent sodium salt leads to a reduction in enzyme function. However, it is known from leaching experiments that prebiotically relevant geomaterial such as basalt releases mainly a lot of sodium and only little magnesium. A natural solution to this problem is heat fluxes through thin rock fractures, through which magnesium is actively enriched and sodium is depleted by thermogravitational convection and thermophoresis. This process establishes suitable conditions for ribozyme function from a basaltic leach. It can take place in a spatially distributed system of rock cracks and is therefore particularly stable to natural fluctuations and disturbances.

• Deficiency of chemical reaction networks and thermodynamics
Matteo Polettini, University of Luxembourg

Deficiency is a topological property of a Chemical Reaction Network linked to important dynamical features, in particular of deterministic fixed points and of stochastic stationary states. Here we link it to thermodynamics: in particular we discuss the validity of a strong vs. weak zeroth law, the existence of time-reversed mass-action kinetics, and the possibility to formulate marginal fluctuation relations. Finally we illustrate some subtleties of the Python module we created for MCMC stochastic simulation of CRNs, soon to be made public.

• Large deviations theory and emergent landscapes in biological dynamics
Hong Qian, University of Washington

The mathematical theory of large deviations provides a nonequilibrium thermodynamic description of complex biological systems that consist of heterogeneous individuals. In terms of the notions of stochastic elementary reactions and pure kinetic species, the continuous-time, integer-valued Markov process dictates a thermodynamic structure that generalizes (i) Gibbs’ microscopic chemical thermodynamics of equilibrium matters to nonequilibrium small systems such as living cells and tissues; and (ii) Gibbs’ potential function to the landscapes for biological dynamics, such as that of C. H. Waddington and S. Wright.

• Using the maximum entropy production principle to understand and predict microbial biogeochemistry
Joseph Vallino, Marine Biological Laboratory, Woods Hole

Natural microbial communities contain billions of individuals per liter and can exceed a trillion cells per liter in sediments, as well as harbor thousands of species in the same volume. The high species diversity contributes to extensive metabolic functional capabilities to extract chemical energy from the environment, such as methanogenesis, sulfate reduction, anaerobic photosynthesis, chemoautotrophy, and many others, most of which are only expressed by bacteria and archaea. Reductionist modeling of natural communities is problematic, as we lack knowledge on growth kinetics for most organisms and have even less understanding on the mechanisms governing predation, viral lysis, and predator avoidance in these systems. As a result, existing models that describe microbial communities contain dozens to hundreds of parameters, and state variables are extensively aggregated. Overall, the models are little more than non-linear parameter fitting exercises that have limited, to no, extrapolation potential, as there are few principles governing organization and function of complex self-assembling systems. Over the last decade, we have been developing a systems approach that models microbial communities as a distributed metabolic network that focuses on metabolic function rather than describing individuals or species. We use an optimization approach to determine which metabolic functions in the network should be up regulated versus those that should be down regulated based on the non-equilibrium thermodynamics principle of maximum entropy production (MEP). Derived from statistical mechanics, MEP proposes that steady state systems will likely organize to maximize free energy dissipation rate. We have extended this conjecture to apply to non-steady state systems and have proposed that living systems maximize entropy production integrated over time and space, while non-living systems maximize instantaneous entropy production. Our presentation will provide a brief overview of the theory and approach, as well as present several examples of applying MEP to describe the biogeochemistry of microbial systems in laboratory experiments and natural ecosystems.

• Reduction and the quasi-steady state approximation
Carsten Wiuf, University of Copenhagen

Chemical reactions often occur at different time-scales. In applications of chemical reaction network theory it is often desirable to reduce a reaction network to a smaller reaction network by elimination of fast species or fast reactions. There exist various techniques for doing so, e.g. the Quasi-Steady-State Approximation or the Rapid Equilibrium Approximation. However, these methods are not always mathematically justifiable. Here, a method is presented for which (so-called) non-interacting species are eliminated by means of QSSA. It is argued that this method is mathematically sound. Various examples are given (Michaelis-Menten mechanism, two-substrate mechanism, …) and older related techniques from the 50s and 60s are briefly discussed.

Non-Equilibrium Thermodynamics in Biology (Part 1)

Together with William Cannon and Larry Li, I’m helping run a minisymposium as part of SMB2021, the annual meeting of the Society for Mathematical Biology:

• Non-equilibrium Thermodynamics in Biology: from Chemical Reaction Networks to Natural Selection, Monday June 14, 2021, beginning 9:30 am Pacific Time.

You can register for free here before May 31st, 11:59 pm Pacific Time. You need to register to watch the talks live on Zoom. I think the talks will be recorded.

Here’s the idea:

Abstract: Since Lotka, physical scientists have argued that living things belong to a class of complex and orderly systems that exist not despite the second law of thermodynamics, but because of it. Life and evolution, through natural selection of dissipative structures, are based on non-equilibrium thermodynamics. The challenge is to develop an understanding of what the respective physical laws can tell us about flows of energy and matter in living systems, and about growth, death and selection. This session will address current challenges including understanding emergence, regulation and control across scales, and entropy production, from metabolism in microbes to evolving ecosystems.

It’s exciting to me because I want to get back into work on thermodynamics and reaction networks, and we’ll have some excellent speakers on these topics. I think the talks will be in this order… later I will learn the exact schedule.

Christof Mast, Ludwig-Maximilians-Universität München

Coauthors: T. Matreux, K. LeVay, A. Schmid, P. Aikkila, L. Belohlavek, Z. Caliskanoglu, E. Salibi, A. Kühnlein, C. Springsklee, B. Scheu, D. B. Dingwell, D. Braun, H. Mutschler.

Title: Heat flows adjust local ion concentrations in favor of prebiotic chemistry

Abstract: Prebiotic reactions often require certain initial concentrations of ions. For example, the activity of RNA enzymes requires a lot of divalent magnesium salt, whereas too much monovalent sodium salt leads to a reduction in enzyme function. However, it is known from leaching experiments that prebiotically relevant geomaterial such as basalt releases mainly a lot of sodium and only little magnesium. A natural solution to this problem is heat fluxes through thin rock fractures, through which magnesium is actively enriched and sodium is depleted by thermogravitational convection and thermophoresis. This process establishes suitable conditions for ribozyme function from a basaltic leach. It can take place in a spatially distributed system of rock cracks and is therefore particularly stable to natural fluctuations and disturbances.

Supriya Krishnamurthy, Stockholm University

Coauthors: Eric Smith

Title: Stochastic chemical reaction networks

Abstract: The study of chemical reaction networks (CRNs) is a very active field. Earlier well-known results (Feinberg Chem. Enc. Sci. 42 2229 (1987), Anderson et al Bull. Math. Biol. 72 1947 (2010)) identify a topological quantity called deficiency, easy to compute for CRNs of any size, which, when exactly equal to zero, leads to a unique factorized (non-equilibrium) steady-state for these networks. No general results exist however for the steady states of non-zero-deficiency networks. In recent work, we show how to write the full moment-hierarchy for any non-zero-deficiency CRN obeying mass-action kinetics, in terms of equations for the factorial moments. Using these, we can recursively predict values for lower moments from higher moments, reversing the procedure usually used to solve moment hierarchies. We show, for non-trivial examples, that in this manner we can predict any moment of interest, for CRNs with non-zero deficiency and non-factorizable steady states. It is however an open question how scalable these techniques are for large networks.

Pierre Gaspard, Université libre de Bruxelles

Title: Nonequilibrium biomolecular information processes

Abstract: Nearly 70 years have passed since the discovery of DNA structure and its role in coding genetic information. Yet, the kinetics and thermodynamics of genetic information processing in DNA replication, transcription, and translation remain poorly understood. These template-directed copolymerization processes are running away from equilibrium, being powered by extracellular energy sources. Recent advances show that their kinetic equations can be exactly solved in terms of so-called iterated function systems. Remarkably, iterated function systems can determine the effects of genome sequence on replication errors, up to a million times faster than kinetic Monte Carlo algorithms. With these new methods, fundamental links can be established between molecular information processing and the second law of thermodynamics, shedding a new light on genetic drift, mutations, and evolution.

Carsten Wiuf, University of Copenhagen

Coauthors: Elisenda Feliu, Sebastian Walcher, Meritxell Sáez

Title: Reduction and the Quasi-Steady State Approximation

Abstract: Chemical reactions often occur at different time-scales. In applications of chemical reaction network theory it is often desirable to reduce a reaction network to a smaller reaction network by elimination of fast species or fast reactions. There exist various techniques for doing so, e.g. the Quasi-Steady-State Approximation or the Rapid Equilibrium Approximation. However, these methods are not always mathematically justifiable. Here, a method is presented for which (so-called) non-interacting species are eliminated by means of QSSA. It is argued that this method is mathematically sound. Various examples are given (Michaelis-Menten mechanism, two-substrate mechanism, …) and older related techniques from the 50-60ies are briefly discussed.

Matteo Polettini, University of Luxembourg

Coauthor: Tobias Fishback

Title: Deficiency of chemical reaction networks and thermodynamics

Abstract: Deficiency is a topological property of a Chemical Reaction Network linked to important dynamical features, in particular of deterministic fixed points and of stochastic stationary states. Here we link it to thermodynamics: in particular we discuss the validity of a strong vs. weak zeroth law, the existence of time-reversed mass-action kinetics, and the possibility to formulate marginal fluctuation relations. Finally we illustrate some subtleties of the Python module we created for MCMC stochastic simulation of CRNs, soon to be made public.

Ken Dill, Stony Brook University

Title: The principle of maximum caliber of nonequilibria

Abstract: Maximum Caliber is a principle for inferring pathways and rate distributions of kinetic processes. The structure and foundations of MaxCal are much like those of Maximum Entropy for static distributions. We have explored how MaxCal may serve as a general variational principle for nonequilibrium statistical physics – giving well-known results, such as the Green-Kubo relations, Onsager’s reciprocal relations and Prigogine’s Minimum Entropy Production principle near equilibrium, but is also applicable far from equilibrium. I will also discuss some applications, such as finding reaction coordinates in molecular simulations non-linear dynamics in gene circuits, power-law-tail distributions in “social-physics” networks, and others.

Joseph Vallino, Marine Biological Laboratory, Woods Hole

Coauthors: Ioannis Tsakalakis, Julie A. Huber

Title: Using the maximum entropy production principle to understand and predict microbial biogeochemistry

Abstract: Natural microbial communities contain billions of individuals per liter and can exceed a trillion cells per liter in sediments, as well as harbor thousands of species in the same volume. The high species diversity contributes to extensive metabolic functional capabilities to extract chemical energy from the environment, such as methanogenesis, sulfate reduction, anaerobic photosynthesis, chemoautotrophy, and many others, most of which are only expressed by bacteria and archaea. Reductionist modeling of natural communities is problematic, as we lack knowledge on growth kinetics for most organisms and have even less understanding on the mechanisms governing predation, viral lysis, and predator avoidance in these systems. As a result, existing models that describe microbial communities contain dozens to hundreds of parameters, and state variables are extensively aggregated. Overall, the models are little more than non-linear parameter fitting exercises that have limited, to no, extrapolation potential, as there are few principles governing organization and function of complex self-assembling systems. Over the last decade, we have been developing a systems approach that models microbial communities as a distributed metabolic network that focuses on metabolic function rather than describing individuals or species. We use an optimization approach to determine which metabolic functions in the network should be up regulated versus those that should be down regulated based on the non-equilibrium thermodynamics principle of maximum entropy production (MEP). Derived from statistical mechanics, MEP proposes that steady state systems will likely organize to maximize free energy dissipation rate. We have extended this conjecture to apply to non-steady state systems and have proposed that living systems maximize entropy production integrated over time and space, while non-living systems maximize instantaneous entropy production. Our presentation will provide a brief overview of the theory and approach, as well as present several examples of applying MEP to describe the biogeochemistry of microbial systems in laboratory experiments and natural ecosystems.

Gheorge Craciun, University of Wisconsin-Madison

Title: Persistence, permanence, and global stability in reaction network models: some results inspired by thermodynamic principles

Abstract: The standard mathematical model for the dynamics of concentrations in biochemical networks is called mass-action kinetics. We describe mass-action kinetics and discuss the connection between special classes of mass-action systems (such as detailed balanced and complex balanced systems) and the Boltzmann equation. We also discuss the connection between the “global attractor conjecture” for complex balanced mass-action systems and Boltzmann’s H-theorem. We also describe some implications for biochemical mechanisms that implement noise filtering and cellular homeostasis.

Hong Qian, University of Washington

Title: Large deviations theory and emergent landscapes in biological dynamics

Abstract: The mathematical theory of large deviations provides a nonequilibrium thermodynamic description of complex biological systems that consist of heterogeneous individuals. In terms of the notions of stochastic elementary reactions and pure kinetic species, the continuous-time, integer-valued Markov process dictates a thermodynamic structure that generalizes (i) Gibbs’ macroscopic chemical thermodynamics of equilibrium matters to nonequilibrium small systems such as living cells and tissues; and (ii) Gibbs’ potential function to the landscapes for biological dynamics, such as that of C. H. Waddington’s and S. Wright’s.

John Harte, University of Berkeley

Coauthors: Micah Brush, Kaito Umemura

Title: Nonequilibrium dynamics of disturbed ecosystems

Abstract: The Maximum Entropy Theory of Ecology (METE) predicts the shapes of macroecological metrics in relatively static ecosystems, across spatial scales, taxonomic categories, and habitats, using constraints imposed by static state variables. In disturbed ecosystems, however, with time-varying state variables, its predictions often fail. We extend macroecological theory from static to dynamic, by combining the MaxEnt inference procedure with explicit mechanisms governing disturbance. In the static limit, the resulting theory, DynaMETE, reduces to METE but also predicts a new scaling relationship among static state variables. Under disturbances, expressed as shifts in demographic, ontogenic growth, or migration rates, DynaMETE predicts the time trajectories of the state variables as well as the time-varying shapes of macroecological metrics such as the species abundance distribution and the distribution of metabolic rates over individuals. An iterative procedure for solving the dynamic theory is presented. Characteristic signatures of the deviation from static predictions of macroecological patterns are shown to result from different kinds of disturbance. By combining MaxEnt inference with explicit dynamical mechanisms of disturbance, DynaMETE is a candidate theory of macroecology for ecosystems responding to anthropogenic or natural disturbances.

Serpentine Barrens

 

This is the Soldiers Delight Natural Environmental Area, a nature reserve in Maryland. The early colonial records of Maryland describe the area as a hunting ground for Native Americans. In 1693, rangers in the King’s service from a nearby garrison patrolled this area and named it Soldiers Delight, for some unknown reason.

It may not look like much, but that’s exactly the point! In this otherwise lush land, why does it look like nothing but grass and a few scattered trees are growing here?

It’s because this area is a serpentine barrens. Serpentine is a kind of rock: actually a class of closely related minerals which get their name from their smooth or scaly green appearance.

Soils formed from serpentine are toxic to many plants because they have lots of nickel, chromium, and cobalt! Plants are also discouraged by how these soils have little potassium and phosphorus, not much calcium, and too much magnesium. Serpentine, you see, is made of magnesium, silicon, iron, hydrogen and oxygen.

As a result, the plants that actually do well in serpentine barrens are very specialized: some small beautiful flowers, for example. Indeed, there are nature reserves devoted to protecting these! One of the most dramatic is the Tablelands of Gros Morne National Park in Newfoundland:

Scott Weidensaul writes this about the Tablelands:

These are hardly garden spots, and virtually no animals live here except for birds and the odd caribou passing through. Yet some plants manage to eke out a living. Balsam ragwort, a relative of the cat’s-paw ragwort of the shale barrens, has managed to cope with the toxins and can tolerate up to 12 percent of its dry weight in magnesium—a concentration that would level most flowers. Even the common pitcher-plant, a species normally associated with bogs, has a niche in this near-desert, growing along the edges of spring seeps where subsurface water brings up a little calcium. By supplementing soil nourishment with a diet of insects trapped in its upright tubes, the pitcher-plant is able to augment the Tablelands’ miserly offerings. Several other carnivorous plants, including sundews and butterwort, work the same trick on their environment.

In North America, serpentine barrens can be found in the Appalachian Mountains—Gros Morne is at the northern end of these, and further south are the Soldiers Delight Natural Environmental Area in Maryland, and the State Line Serpentine Barrens on the border of Maryland and Pennsylvania.

There are also serpentine barrens in the coastal ranges of California, Oregon, and Washington. Here are some well-adapted flowers in the Klamath-Siskiyou Mountains on the border of California and Oregon:

I first thought about serpentine when the Azimuth Project was exploring ways of sucking carbon dioxide from the air. If you grind up serpentine and get it wet, it will absorb carbon dioxide! A kilogram of serpentine can dispose about two-thirds of a kilogram of carbon dioxide. So, people have suggested this as a way to fight global warming.

Unfortunately we’re putting out over 37 gigatonnes of carbon dioxide per year. To absorb all of this we’d need to grind up about 55 gigatonnes of serpentine every year, spread it around, and get it wet. There’s plenty of serpentine available, but this is over ten times the amount of worldwide cement production, so it would take a lot of work. Then there’s the question of where to put all the ground-up rock.

And now I’ve learned that serpentine poses serious challenges to the growth of plant life! It doesn’t much matter, given that nobody seems eager to fight global warming by grinding up huge amounts of this rock. But it’s interesting.

Credits

The top picture of the Soldiers Delight Natural Environmental Area was taken by someone named Veggies. The picture of serpentine was apparently taken by Kluka. The Tablelands were photographed by Tango7174. All these are on Wikicommons. The quote comes from this wonderful book:

• Scott Weidensaul, Mountains of the Heart: A Natural History of the Appalachians, Fulcrum Publishing, 2016.

The picture of flowers in the Klamath-Siskiyous was taken by Susan Erwin and appears along with many other interesting things here:

• Klamath-Siskiyou serpentines, U. S. Forest Service.

A quote:

It is crystal clear when you have entered the serpentine realm. There is no mistaking it, as the vegetation shift is sharp and dramatic. Full-canopied forests become sparse woodlands or barrens sometimes in a matter of a few feet. Dwarfed trees, low-lying shrubs, grassy patches, and rock characterize the dry, serpentine uplands. Carnivorous wetlands, meadows, and Port-Orford-cedar dominated riparian areas express the water that finds its way to the surface through fractured and faulted bedrock.

For more on serpentine, serpentinization, and serpentine barrens, try this blog article:

• Serpentine, Hiker’s Notebook.

It’s enjoyable despite its misuse of the word ‘Weltanschauung’.

Shinise

 

The Japanese take pride in ‘shinise’: businesses that have lasted for hundreds or even thousands of years. This points out an interesting alternative to the goal of profit maximization: maximizing the time of survival.

• Ben Dooley and Hisako Ueno, This Japanese shop is 1,020 years old. It knows a bit about surviving crises, New York Times, 2 December 2020.

Such enterprises may be less dynamic than those in other countries. But their resilience offers lessons for businesses in places like the United States, where the coronavirus has forced tens of thousands into bankruptcy.

“If you look at the economics textbooks, enterprises are supposed to be maximizing profits, scaling up their size, market share and growth rate. But these companies’ operating principles are completely different,” said Kenji Matsuoka, a professor emeritus of business at Ryukoku University in Kyoto.

“Their No. 1 priority is carrying on,” he added. “Each generation is like a runner in a relay race. What’s important is passing the baton.”

Japan is an old-business superpower. The country is home to more than 33,000 with at least 100 years of history — over 40 percent of the world’s total. Over 3,100 have been running for at least two centuries. Around 140 have existed for more than 500 years. And at least 19 claim to have been continuously operating since the first millennium.

(Some of the oldest companies, including Ichiwa, cannot definitively trace their history back to their founding, but their timelines are accepted by the government, scholars and — in Ichiwa’s case — the competing mochi shop across the street.)

The businesses, known as “shinise,” are a source of both pride and fascination. Regional governments promote their products. Business management books explain the secrets of their success. And entire travel guides are devoted to them.

Of course if some businesses try to maximize time of survival, they may be small compared to businesses that are mainly trying to become “big”—at least if size is not the best road to long-term survival, which apparently it’s not. So we’ll have short-lived dinosaurs tromping around, and, dodging their footsteps, long-lived mice.

The idea of different organisms pursuing different strategies is familiar in ecology, where people talk about r-selected and K-selected organisms. The former “emphasize high growth rates, typically exploit less-crowded ecological niches, and produce many offspring, each of which has a relatively low probability of surviving to adulthood.” The latter “display traits associated with living at densities close to carrying capacity and typically are strong competitors in such crowded niches, that invest more heavily in fewer offspring, each of which has a relatively high probability of surviving to adulthood.”

But the contrast between r-selection and K-selection seems different to me than the contrast between profit maximization and lifespan maximization. As far as I know, no organism except humans deliberately tries to maximize the lifetime of anything.

And amusingly, the theory of r-selection versus K-selection may also be nearing the end of its life:

When Stearns reviewed the status of the theory in 1992, he noted that from 1977 to 1982 there was an average of 42 references to the theory per year in the BIOSIS literature search service, but from 1984 to 1989 the average dropped to 16 per year and continued to decline. He concluded that r/K theory was a once useful heuristic that no longer serves a purpose in life history theory.

For newer thoughts, see:

• D. Reznick, M. J. Bryant and F. Bashey, r-and K-selection revisited: the role of population regulation in life-history evolution, Ecology 83 (2002) 1509–1520.

See also:

• Innan Sasaki, How to build a business that lasts more than 200 years—lessons from Japan’s shinise companies, The Conversation, 6 June 2019.

Among other things, she writes:

We also found there to be a dark side to the success of these age-old shinise firms. At least half of the 17 companies we interviewed spoke of hardships in maintaining their high social status. They experienced peer pressure not to innovate (and solely focus on maintaining tradition) and had to make personal sacrifices to maintain their family and business continuity.

As the vice president of Shioyoshiken, a sweets company established in 1884, told us:

In a shinise, the firm is the same as the family. We need to sacrifice our own will and our own feelings and what we want to do … Inheriting and continuing the household is very important … We do not continue the business because we particularly like that industry. The fact that our family makes sweets is a coincidence. What is important is to continue the household as it is.

Innovations were sometimes discouraged by either the earlier family generation who were keen on maintaining the tradition, or peer shinise firms who cared about maintaining the tradition of the industry as a whole. Ultimately, we found that these businesses achieve such a long life through long-term sacrifice at both the personal and organisational level.

Fisher’s Fundamental Theorem (Part 3)

Last time we stated and proved a simple version of Fisher’s fundamental theorem of natural selection, which says that under some conditions, the rate of increase of the mean fitness equals the variance of the fitness. But the conditions we gave were very restrictive: namely, that the fitness of each species of replicator is constant, not depending on how many of these replicators there are, or any other replicators.

To broaden the scope of Fisher’s fundamental theorem we need to do one of two things:

1) change the left side of the equation: talk about some other quantity other than rate of change of mean fitness.

2) change the right side of the question: talk about some other quantity than the variance in fitness.

Or we could do both! People have spent a lot of time generalizing Fisher’s fundamental theorem. I don’t think there are, or should be, any hard rules on what counts as a generalization.

But today we’ll take alternative 1). We’ll show the square of something called the ‘Fisher speed’ always equals the variance in fitness. One nice thing about this result is that we can drop the restrictive condition I mentioned. Another nice thing is that the Fisher speed is a concept from information theory! It’s defined using the Fisher metric on the space of probability distributions.

And yes—that metric is named after the same guy who proved Fisher’s fundamental theorem! So, arguably, Fisher should have proved this generalization of Fisher’s fundamental theorem. But in fact it seems that I was the first to prove it, around February 1st, 2017. Some similar results were already known, and I will discuss those someday. But they’re a bit different.

A good way to think about the Fisher speed is that it’s ‘the rate at which information is being updated’. A population of replicators of different species gives a probability distribution. Like any probability distribution, this has information in it. As the populations of our replicators change, the Fisher speed says the rate at which this information is being updated. So, in simple terms, we’ll show

The square of the rate at which information is updated is equal to the variance in fitness.

This is quite a change from Fisher’s original idea, namely:

The rate of increase of mean fitness is equal to the variance in fitness.

But it has the advantage of always being true… as long the population dynamics are described by the general framework we introduced last time. So let me remind you of the general setup, and then prove the result!

The setup

We start out with population functions 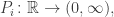one for each species of replicator obeying the Lotka–Volterra equation

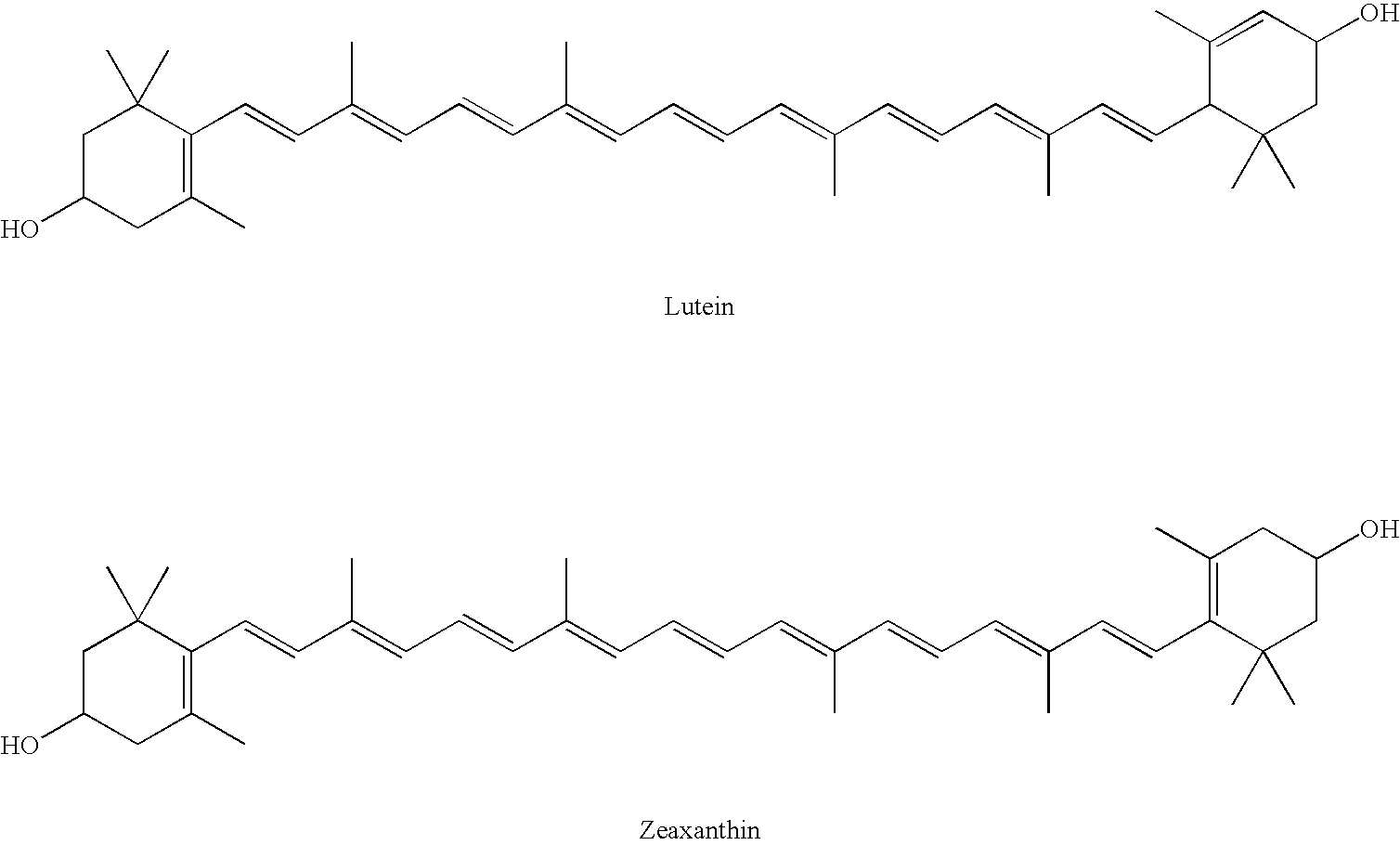
for some differentiable functions called fitness functions. The probability of a replicator being in the ith species is

Using the Lotka–Volterra equation we showed last time that these probabilities obey the replicator equation

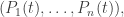Here is short for the whole list of populations and

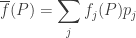
is the mean fitness.

The Fisher metric

The space of probability distributions on the set 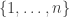is called the (n-1)-simplex

It’s called because it’s (n-1)-dimensional. When it looks like the letter

The Fisher metric is a Riemannian metric on the interior of the (n-1)-simplex. That is, given a point in the interior of and two tangent vectors 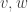at this point the Fisher metric gives a number

Here we are describing the tangent vectors 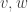as vectors in 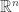with the property that the sum of their components is zero: that’s what makes them tangent to the (n-1)-simplex. And we’re demanding that be in the interior of the simplex to avoid dividing by zero, since on the boundary of the simplex we have for at least one choice of $i.$

If we have a probability distribution 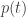moving around in the interior of the (n-1)-simplex as a function of time, its Fisher speed is

if the derivative exists. This is the usual formula for the speed of a curve moving in a Riemannian manifold, specialized to the case at hand.

Now we’ve got all the formulas we’ll need to prove the result we want. But for those who don’t already know and love it, it’s worthwhile saying a bit more about the Fisher metric.

The factor of in the Fisher metric changes the geometry of the simplex so that it becomes round, like a portion of a sphere:

But the reason the Fisher metric is important, I think, is its connection to relative information. Given two probability distributions 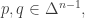the information of relative to is

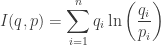
You can show this is the expected amount of information gained if was your prior distribution and you receive information that causes you to update your prior to So, sometimes it’s called the information gain. It’s also called relative entropy or—my least favorite, since it sounds so mysterious—the Kullback–Leibler divergence.

Suppose 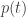is a smooth curve in the interior of the (n-1)-simplex. We can ask the rate at which information is gained as time passes. Perhaps surprisingly, a calculation gives

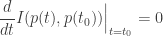
That is, in some sense ‘to first order’ no information is being gained at any moment However, we have

So, the square of the Fisher speed has a nice interpretation in terms of relative entropy!

For a derivation of these last two equations, see Part 7 of my posts on information geometry. For more on the meaning of relative entropy, see Part 6.

The result

It’s now extremely easy to show what we want, but let me state it formally so all the assumptions are crystal clear.

Theorem. Suppose the functions obey the Lotka–Volterra equations:

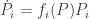
for some differentiable functions called fitness functions. Define probabilities and the mean fitness as above, and define the variance of the fitness by

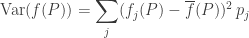
Then if none of the populations 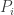are zero, the square of the Fisher speed of the probability distribution is the variance of the fitness:

Proof. The proof is near-instantaneous. We take the square of the Fisher speed:

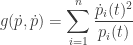
and plug in the replicator equation:

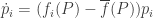
We obtain:

as desired.   █

It’s hard to imagine anything simpler than this. We see that given the Lotka–Volterra equation, what causes information to be updated is nothing more and nothing less than variance in fitness!

---

The whole series:

• Part 1: the obscurity of Fisher’s original paper.

• Part 2: a precise statement of Fisher’s fundamental theorem of natural selection, and conditions under which it holds.

• Part 3: a modified version of the fundamental theorem of natural selection, which holds much more generally.

• Part 4: my paper on the fundamental theorem of natural selection.

Markov Decision Processes

The National Institute of Mathematical and Biological Sciences is having an online seminar on ‘adaptive management’. It should be fun for people who want to understand Markov decision processes—like me!

• NIMBioS Adaptive Management Webinar Series, 2020 October 26-29 (Monday-Thursday).

Adaptive management seeks to determine sound management strategies in the face of uncertainty concerning the behavior of the system being managed. Specifically, it attempts to find strategies for managing dynamic systems while learning the behavior of the system. These webinars review the key concept of a Markov Decision Process (MDP) and demonstrate how quantitative adaptive management strategies can be developed using MDPs. Additional conceptual, computational and application aspects will be discussed, including dynamic programming and Bayesian formalization of learning.

Here are the topics:

Session 1: Introduction to decision problems
Session 2: Introduction to Markov decision processes (MDPs)
Session 3: Solving Markov decision processes (MDPs)
Session 4: Modeling beliefs
Session 5: Conjugacy and discrete model adaptive management (AM)
Session 6: More on AM problems (Dirichlet/multinomial and Gaussian prior/likelihood)
Session 7: Partially observable Markov decision processes (POMDPs)
Session 8: Frontier topics (projection methods, approximate DP, communicating solutions)