This picture by Roice Nelson shows a remarkable structure: the hexagonal tiling honeycomb.
What is it? Roughly speaking, a honeycomb is a way of filling 3d space with polyhedra. The most symmetrical honeycombs are the ‘regular’ ones. For any honeycomb, we define a flag to be a chosen vertex lying on a chosen edge lying on a chosen face lying on a chosen polyhedron. A honeycomb is regular if its geometrical symmetries act transitively on flags.
The most familiar regular honeycomb is the usual way of filling Euclidean space with cubes. This cubic honeycomb is denoted by the symbol {4,3,4}, because a square has 4 edges, 3 squares meet at each corner of a cube, and 4 cubes meet along each edge of this honeycomb. We can also define regular honeycombs in hyperbolic space. For example, the order-5 cubic honeycomb is a hyperbolic honeycomb denoted {4,3,5}, since 5 cubes meet along each edge:
Coxeter showed there are 15 regular hyperbolic honeycombs. The hexagonal tiling honeycomb is one of these. But it does not contain polyhedra of the usual sort! Instead, it contains flat Euclidean planes embedded in hyperbolic space, each plane containing the vertices of infinitely many regular hexagons. You can think of such a sheet of hexagons as a generalized polyhedron with infinitely many faces. You can see a bunch of such sheets in the picture:
The symbol for the hexagonal tiling honeycomb is {6,3,3}, because a hexagon has 6 edges, 3 hexagons meet at each corner in a plane tiled by regular hexagons, and 3 such planes meet along each edge of this honeycomb. You can see that too if you look carefully.
A flat Euclidean plane in hyperbolic space is called a horosphere. Here’s a picture of a horosphere tiled with regular hexagons, yet again drawn by Roice:
Unlike the previous pictures, which are views from inside hyperbolic space, this uses the Poincaré ball model of hyperbolic space. As you can see here, a horosphere is a limiting case of a sphere in hyperbolic space, where one point of the sphere has become a ‘point at infinity’.
Be careful. A horosphere is intrinsically flat, so if you draw regular hexagons on it their internal angles are
as usual in Euclidean geometry. But a horosphere is not ‘totally geodesic’: straight lines in the horosphere are not geodesics in hyperbolic space! Thus, a hexagon in hyperbolic space with the same vertices as one of the hexagons in the horosphere actually bulges out from the horosphere a bit — and its internal angles are less than : they are
This angle may be familar if you’ve studied tetrahedra. That’s because each vertex lies at the center of a regular tetrahedron, with its four nearest neighbors forming the tetrahedron’s corners.
It’s really these hexagons in hyperbolic space that are faces of the hexagonal tiling honeycomb, not those tiling the horospheres, though perhaps you can barely see the difference. This can be quite confusing until you think about a simpler example, like the difference between a cube in Euclidean 3-space and a cube drawn on a sphere in Euclidean space.
Connection to special relativity
There’s an interesting connection between hyperbolic space, special relativity, and 2×2 matrices. You see, in special relativity, Minkowski spacetime is equipped with the nondegenerate bilinear form
usually called the Minkowski metric. Hyperbolic space sits inside Minowski spacetime as the hyperboloid of points with
and
But we can also think of Minkowski spacetime as the space
of 2×2 hermitian matrices, using the fact that every such matrix is of the form
and
In these terms, the future cone in Minkowski spacetime is the cone of positive definite hermitian matrices:
Sitting inside this we have the hyperboloid
which is none other than hyperbolic space!
Connection to the Eisenstein integers
Since the hexagonal tiling honeycomb lives inside hyperbolic space, which in turn lives inside Minkowski spacetime, we should be able to describe the hexagonal tiling honeycomb as sitting inside Minkowski spacetime. But how?
Back in 2022, James Dolan and I conjectured such a description, which takes advantage of the picture of Minkowski spacetime in terms of 2×2 matrices. And this April, working on Mathstodon, Greg Egan and I proved this conjecture!
I’ll just describe the basic idea here, and refer you elsewhere for details.
The Eisenstein integers are the complex numbers of the form
where and
are integers and
is a cube root of 1. The Eisenstein integers are closed under addition, subtraction and multiplication, and they form a lattice in the complex numbers:
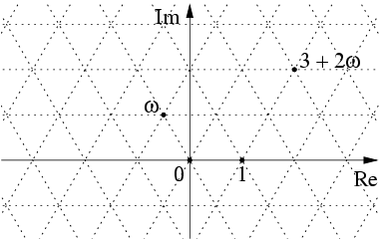
Similarly, the set of 2×2 hermitian matrices with Eisenstein integer entries gives a lattice in Minkowski spacetime, since we can describe Minkowski spacetime as
Here’s the conjecture:
Conjecture. The points in the lattice that lie on the hyperboloid
are the centers of hexagons in a hexagonal tiling honeycomb.
Using known results, it’s relatively easy to show that there’s a hexagonal tiling honeycomb whose hexagon centers are all points in The hard part is showing that every point in
is a hexagon center. Points in
are the same as 4-tuples of integers obeying an inequality (the
condition) and a quadratic equation (the
condition). So, we’re trying to show that all 4-tuples obeying those constraints follow a very regular pattern.
Here are two proofs of the conjecture:
• John Baez, Line bundles on complex tori (part 5), The n-Category Café, April 30, 2024.
Greg Egan and I came up with the first proof. The basic idea was to assume there’s a point in that’s not a hexagon center, choose one as close as possible to the identity matrix, and then construct an even closer one, getting a contradiction. Shortly thereafter, someone on Mastodon by the name of Mist came up with a second proof, similar in strategy but different in detail. This increased my confidence in the result.
What’s next?
Something very similar should be true for another regular hyperbolic honeycomb, the square tiling honeycomb:
Here instead of the Eisenstein integers we should use the Gaussian integers, , consisting of all complex numbers
where and
are integers.
Conjecture. The points in the lattice that lie on the hyperboloid
are the centers of squares in a square tiling honeycomb.
I’m also very interested in how these results connect to algebraic geometry! I explained this in some detail here:
• Line bundles on complex tori (part 4), The n-Category Café, April 26, 2024.
Briefly, the hexagon centers in the hexagonal tiling honeycomb correspond to principal polarizations of the abelian variety . These are concepts that algebraic geometers know and love. Similarly, if the conjecture above is true, the square centers in the square tiling honeycomb will correspond to principal polarizations of the abelian variety
. But I’m especially interested in interpreting the other features of these honeycombs — not just the hexagon and square centers — using ideas from algebraic geometry.







 Posted by John Baez
Posted by John Baez 












