An important early tuning system is Pythagorean tuning, where we force all frequency ratios to involve only powers of 2 and 3. In music, 3/2 is the ‘fifth’: the most consonant of intervals except for the octave.
If we start with some frequency and go up and down by powers of 3/2, we create the ‘circle of fifths’ shown above. It’s almost a 12-pointed star, with one point for each note in the 12-tone equal-tempered scale.
Almost—but not quite! When we go up 12 fifths, we get a tone that’s almost but not quite 2⁷ times the frequency we started with. In other words, it’s almost but not quite 7 octaves higher. So there’s a glitch.
Here I’ve stuck that glitch at the opposite from the pitch labeled 1. That’s a good place for it, because the spot directly opposite 1 is called the ‘tritone’, or sometimes diabolus in musica: the ‘devil in music’. 😈
Let me explain the chart a bit more carefully. I started with any pitch and arbitrarily called its frequency 1. Then I climbed up 6 fifths, multiplying the frequency by 3/2 each time, getting pitches with frequencies
Going all the way around the circle clockwise means going up an octave: that is, multiplying the frequency by 2. So each time I multiplied the frequency by 3/2, I went log2(3/2) of the way clockwise around the circle: that is, about 0.585 of the way around, a bit more than half-way.
Then I climbed down 6 fifths, going counterclockwise and dividing the frequency by 3/2 each time, getting pitches with frequencies
These are the reciprocals of the numbers we saw going up.
Why did I stop when I did? 729/64 is nowhere close to 64/729, but their ratio is almost a power of 2:
while
So our star is close to a 12-pointed star. But there’s a glitch. And the size of the glitch is called the Pythagorean comma:
You can listen to two tones separated by a Pythagorean comma here. This discrepancy is one of the problems afflicting Pythagorean tuning, and later I’ll say a bit about how people deal with it.
Now let’s multiply the frequencies we’ve seen by powers of 2 to make them lie between 1 and 2. That gives us a scale that lies within a single octave:
These different pitches have names, by the way! Not just in Pythagorean tuning but in other related tuning systems, like the equal-tempered scale widely used in music today. Here they are:
In the equal-tempered scale there’s no difference between the augmented 4th and the diminished 5th: they’re both the tritone. But in Pythagorean tuning they’re different. And surprisingly, the augmented 4th is higher in pitch than the diminished 5th.
It may or may not help you to see the abbreviations for these different pitch names:
I could talk about this chart all day, but most of what I’d say would apply just as well to the equal-tempered scale. The big difference is that in Pythagorean tuning, unlike the equal-tempered scale, the augmented 4th (A4) and diminished fifth (d5) are not the same note. They are very close: the chart is not to scale, and if it were these two pitches would be almost on top of each other. But they’re not the same!
It also may or may not help you to see the names for these pitches when the frequency we arbitrarily called 1 is the note called C:
We get a funny version of the scale with 13 notes, because F sharp (the augmented 4th in the key of C) is different from G flat (the diminished 5th).
Okay, but what if we want a scale with just 12 notes? We usually remove the diminished 5th, and make the augmented 4th do whatever jobs the diminished 5th would have done! So, we change our chart to this:
Or, in terms of frequencies, this:
This looks terrible, but more importantly it creates a badly out-of-tune pair of notes, namely those connected by the new red edge. These pitches have an ugly frequency ratio of
If we hadn’t used the augmented 4th for a job the diminished 5th should be doing, we’d have gotten the much nicer-sounding ratio
The difference is audible and unpleasant: we’ve created what’s called a ‘wolf interval’, called that because it howls like a wolf. Unsurprisingly, the ugly ratio divided by the nicer ratio is our old nemesis, the Pythagorean comma:
It’s interesting to look at the frequency ratios of neighboring notes in the Pythagorean scale:
In the equal-tempered scale the frequency ratio of neighboring notes is always 21/12, and it’s called a semitone. But as you can see, in the Pythagorean scale some neighboring notes have a frequency ratio of 256/243, while others have a ratio of 2187/2048. So there are two kinds of semitones in the Pythagorean scale:
• 256/243 = 283-5 is called the Pythagorean diatonic semitone or Pythagorean limma. You can get it by going down 5 fifths and then up 3 octaves:
• 2187/2048 = 2-1137 is called the Pythagorean chromatic semitone or Pythagorean apotome. You can get it by going up 7 fifths and then down 4 octaves:
The Pythagorean chromatic semitone is bigger than the Pythagorean diatonic semitone. How much bigger? What’s their ratio?
Yes, it’s the Pythagorean comma! Like a bad penny, it keeps coming back to haunt us.
By the way, the word ‘limma’ is from a Greek word meaning ‘remnant’, and it’s used for several small intervals in music. The word ‘apotome’ is from a Greek word meaning ‘cutting off’, and it’s apparently used only for this particular interval, as well as other things in mathematics and optics.
The somewhat irregular pattern of semitones in my chart above would become symmetrical if we had kept the diminished 5th, but then there would be a Pythagorean comma between the augmented 4th and diminished 5th, like this:
Now the chart is symmetrical from top to bottom. The big nasty fraction in the middle is the Pythagorean comma:
Besides the Pythagorean comma—and the wolf interval we get if we try to avoid it—another big problem with Pythagorean tuning is that some very important intervals are represented by fairly complicated fractions. The ear seems to enjoy simple fractions! There are other tuning systems that do better at this, like ‘just intonation’. For example, in Pythagorean tuning the minor third is 32/27 above the tonic, while in just intonation it’s 6/5. In Pythagorean tuning the major third is a ridiculous 81/64 above the tonic, while in just intonation it’s 5/4. Arguably just intonation gets these things right, while Pythagorean tuning gets them wrong.
I hope to write more about just intonation later! To finish off, here’s a comparison between Pythagorean tuning and equal temperament:
I’m not trying to imply that equal temperament is ‘correct’, but at right I’m showing the Pythagorean frequency divided by the corresponding equal-tempered frequency. It’s a bit remarkable how close they are! The biggest deviations occur for the augmented 4th and diminished 5th, which are the same in equal temperament but separated by a comma in the Pythagorean scale. The second biggest deviations occur for the minor 2nd and major 7th. All these are fairly dissonant intervals even in the best of worlds. But the third biggest occur for the major 3rd and minor 6th.
Here’s a picture comparing Pythagorean tuning and equal temperament:
Equal-tempered is black and Pythagorean is green. You can see the diminished fifth and augmented fourth straddling the tritone.
So much more to say! And I want to get back to talking about modes, too. The appearance of the circle of fifths in both is far from a coincidence! But I’ll quit here for now.
For more on just intonation, read this series:
For more on quarter-comma meantone tuning, read this series:
For more on well-tempered scales, read this series:
For more on equal temperament, read this series:
Azimuth 
On the contrary, everything that you've written here implies that equal temperament is not at all correct! Pythagorean tuning has all of these problems with complicated fractions, but equal temperament is infinitely worse, since every interval (other than an octave) is irrational.
The only reason why equal temperament sounds acceptable to us (besides our being used to it) is that our ears just aren't good enough to tell the difference between an irrational interval and a nearby rational interval. (That also makes Pythagorean tuning not as bad as it might be; a complicated fraction can sound like a nearby simple fraction.) And for those who can hear the difference, well, maybe Pythagorean tuning or (even better) just temperament is necessary.
Incidentally, Bach's Well Tempered Clavier was written to show off the sounds of all 12 major and minor keys in just temperament. (They're all different; each key has its own unique character.) If you play it on a modern equal-tempered keyboard, then you're not hearing what he was trying to show us.
Thanks! I agree with all this except I don’t think Bach’s Well Tempered Clavier was written to show off just temperament (assuming this is the same as what I call just intonation). I believe these pieces would sound pretty bad in just intonation, which has some severe wolf intervals. A ‘temperament’ is usually defined to be a way of tweaking just intonation to make it more usable in multiple scales:
• Wikipedia, Musical temperament.
People seem to agree the Well Tempered Clavier was written to show off some ‘well tempered’ tuning system. Unfortunately there are a number of possibilities, and nobody knows which one Bach was using—he never said! In fact people have been reduced to looking at a doodle on Bach’s manuscript and trying to interpret it as a tuning system.
For more, try this:
• Wikipedia, Bach temperament.
By the way, after you made your comment I added something fun to my article. I worked out the ratio of the chromatic and diatonic Pythagorean semitones!
I didn’t realize that there was all this controversy! But any solution is going to have some bad intervals; what makes the different keys different is that these appear in different places. So I'd expect Bach to write his pieces to avoid them (or else to use them deliberately for effect).
So, theoretically someone could try to infer the well-tempered scale Bach used, from among the most likely candidates, by examining how nice they’d make The Well-Tempered Clavier sound! I imagine someone must have tried this.
About the last table of comparison between Pythagorean tuning and equal temperament, we can also do it for major/minor chords (and for many other tunings) and compare their consonance using Plomp and Levelt’s formula (although it has its limitations):
Thanks, I’ll definitely read this. I hadn’t known you had written about tuning systems. It’s good to hear from you!
One thing that has always left me perplexed is the short exact sequence
. Between considering lattices of tones built on ratios such as 3/2 and 2/1, and a closed system of 12 tones, one would thing that there is only a short step, yet I can’t quite make this work.
That’s a great question! I’ve been working on some ideas relating tuning theory to lattices (in the way you mentioned) and then to Coxeter groups and modular functions (in ways I hope to explain someday). But I had not thought of trying to get the musical
to show up “automatically” from the theory of lattices by using the fact that it’s the abelianization of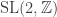 
(as you are essentially pointing out here). That would be amazing. Even though I’ve written about this way of getting 
elsewhere, it had not occurred to me in the context of music theory.
I’ll think about it! But it may be “too good to be true”.
https://en.wikipedia.org/wiki/The_Wolfe_Tones
There’s another interesting thing to be learned from this chart together with the fact that the ratio
is the Pythagorean ratio. Multiplying all the fractions at right we get 2, but we also get 7 factors of 256/243 and 5 factors of 2187/2048 = P · 256/243. So,
or
This must of course be compatible with the definition of
as 312 · 2-19.
It’s interesting that if you play a major scale starting with your tonic in this tuning (or any other diatonic scale using the same notes), then all five whole steps have the same frequency ratio (9/8) and both half steps have the same frequency ratio (256/243). Of course that’s true of every scale with equal temperament, but it’s not true of most scales (or any reasonable scales?) in just temperament. It would be interesting to hear if that makes Pythagorean tuning sound better than just tuning if you only play white-key melodies, without any harmonies.
I don’t know much about the history of tuning systems and scales. I wonder if this property of this tuning system might have contributed to the dominance of diatonic scales in Western music and their prevalence elsewhere.
Mark wrote:
That’s an interesting observation! I was being a bit odd focusing so much on the chromatic version of the Pythagorean scale and not at all on its diatonic or more precisely major ‘sub-scale’:
which, together with its various modes, is probably how people actually played music in Pythagorean tuning.
Great question!
I don’t know much about the history of tuning systems, but I’m fascinated by it. Wikipedia claims Pythagorean tuning was widespread in Europe until about 1500. But just intonation, or more precisely Ptolemy’s intense diatonic scale, goes back at least to Ptolemy’s Harmonics written around 140 AD, and he argued against Pythagorean tuning. I get the feeling that just intonation generally replaced Pythagorean tuning after 1500, and then later got supplanted by quarter-comma meantone, followed by various ‘well-tempered’ scales.
I would love to know more about this. Right now I’m mainly just learning what I need to fully appreciate this amazing article:
• Daniel Muzzulini, Isaac Newton’s microtonal approach to just intonation, Empirical Musical Review 15 (2020).
and then explain some of it.
Out of curiosity, since I’ve seen that you watch a lot of the same music theory-oriented YouTubers that I do, did you find out about the article about Newton via 12tone?
If I’d been smart I would have, since I watched 12tone’s video about Newton. But what happened is that after watching that, I looked around for information about Newton’s work on music theory and quickly ran into that article.
Well, that’s all I meant by “via”. As far as I can tell the Muzzulini article isn’t among the sources that 12tone cites, though the video does get a bit into Newton’s ideas about tuning.
Oh, actually 12tone says this about Newton:
A 4th (what you are calling “Major 4th”) is usually called Perfect 4th. You have it right in the diagrams, as P4.
Also, an Octave is also sometimes called a Perfect 8th, but I have never seen this anywhere except in some of my piano theory teaching books.
Whoops, that “Major 4th” was a slip. I’ll fix it. Thanks!
I’ve never seen “Perfect 8th” or for that matter “Perfect 1st”, even though they’d be logical names.
I find the terms “Major 2nd” and “Minor 2nd” a bit odd since the former is used in both major and minor scales (not counting modes like Phrygian). But I’m happy to go along with standard terminology.
To me, it makes the most sense to think of ‘major’ and ‘minor’ as fundamentally about intervals, and the scales/modes/keys are just named after them. (Which means that the weird thing is calling aeolian ‘minor’ when the real minor mode is phrygian.)
I really don’t get it. For years I’m following you, desperately trying to get category theory. And now you are wasting your time and energy explaining completely trivial tuning things that are known for centuries. At least try to get to understand and explain difficult tuning matters like this: https://www.kees.cc/music/yaphi/yaphi.html
I explain things as I learn them, since I need to write about things to understand them. I’ve been doing this with category theory ever since I first started learning it in the 1980s; I do it for many other subjects too. Now I’m doing it for modes and tuning theory. Wait a while and I may say something interesting. Or not.
I avoid suddenly diving into the ‘difficult’ part of a subject. I did that as a youth, trying to prove some famous conjectures, but I learned this doesn’t work well for me. I make the most progress when I keep thinking about simple things for a long time. In some subjects, I eventually reach the frontiers of what people have thought about and keep right on going. Then learning turns into research. In other cases I just have fun learning stuff.