Tidbits of Geometry

Since I grew up up reading Martin Gardner, I’ve often imagined it would be fun to write about math and physics in a way that nonexperts might enjoy. Right now I’m trying my hand at this on Google+. You can read that stuff here.

Google+ encourages brevity—not as much as Twitter, but more than a blog. So I’m posting things that feature a single catchy image, a brief explanation, and URL’s to visit for more details.

Lately I’ve been talking about geometry. I realized that these posts could be cobbled together into a kind of loose ‘story’, so here it is. I couldn’t resist expanding the posts a bit, but the only really new stuff is more about Leonardo Da Vinci and the golden ratio, and five puzzles—only one of which I know the answer to!

The golden ratio

Sure, the golden ratio, Φ = (√5+1)/2, is cool… but if you think ancient Greeks ran around in togas talking about the “golden ratio” and writing it as “Φ”, you’re wrong. This number was named Φ after the Greek sculptor Phidias only in 1914, in a book called The Curves of Life by the artist Theodore Cook. And it was Cook who first started calling 1.618… the golden ratio. Before him, 1/Φ = 0.618… was called the golden ratio! Cook dubbed this number “φ”, the lower-case baby brother of Φ.

In fact, the whole “golden” terminology can only be traced back to 1826, when it showed up in a footnote to a book by one Martin Ohm, brother of Georg Ohm—the guy with the law about resistors. Before then, a lot of people called 1/Φ the “Divine Proportion”. And the guy who started that was Luca Pacioli, a pal of Leonardo da Vinci who translated Euclid’s Elements. In 1509, Pacioli published a 3-volume text entitled De Divina Proportione, advertising the virtues of this number.

Greek texts seem remarkably quiet about this number. The first recorded hint of it is Proposition 11 in Book II of Euclid’s Elements. It also shows up elsewhere in Euclid, especially Proposition 30 of Book VI, where the task is “to cut a given finite straight line in extreme and mean ratio”, meaning a ratio A:B such that A is to B as B is to A+B. This is later used in Proposition 17 of Book XIII to construct the pentagonal face of a regular dodecahedron.

The regular pentagon, and the pentagram inside it, is deeply connected to the golden ratio. If you look carefully, you’ll see no fewer than twenty long skinny isosceles triangles, in three different sizes but all the same shape!

They’re all ‘golden triangles’: the short side is φ times the length of the long sides.

And the picture here lets us see that φ is to 1 as 1 is to 1+φ. A little algebra then gives

which you can solve to get

and thus

For more, see:

• John Baez, Tales of the Dodecahedron.

Da Vinci and the golden ratio

Did Leonardo da Vinci use the golden ratio in his art? It would cool if he did. Unfortunately, attempts to prove it by drawing rectangles on his sketches and paintings are unconvincing. Here are three attempts you can see on the web; click for details if you want:

The first two make me less inclined to believe Da Vinci was using the golden ratio, not more. The last one, the so-called
Vitruvian Man, looks the most convincing, but only if you take on faith that the ratio being depicted is really the golden ratio!

Puzzle 1. Carefully measure the ratio here and tell us what you get, with error bars on your result.

It would be infinitely more convincing if Da Vinci had written about the golden ratio in his famous notebooks. But I don’t think he did. If he didn’t, that actually weighs against the whole notion.

Indeed, I thought the whole notion was completely hopeless until I discovered that Da Vinci did the woodcuttings for Pacioli’s book De Divina Proportione. And even lived with Pacioli while this project was going on! So, we can safely assume Da Vinci knew what was in this book.

It consists of 3 separate volumes. First a volume about the golden ratio, polygons, and perspective. Then one about the ideas of Vitruvius on math in architecture. (Apparently Vitruvius did not discuss the golden ratio.) Then one that’s mainly an Italian translation of Piero della Francesca’s Latin writings on polyhedra.

De Divina Proportione was popular in its day, but only two copies of the original edition survive. Luckily, it’s been scanned in!

• Luca Pacioli, De Divina Proportione.

The only picture I see that might be about using the golden ratio to draw the human figure is this:

The rectangles don’t look very ‘golden’! But the really important thing is to read the text around this picture, or for that matter the whole book. Unfortunately my Renaissance Italian is… ahem… a bit rusty. The text has been translated into German but apparently not English.

Puzzle 2. What does Luca Pacioli say on this page?

The picture above is on page 70 of the scanned-in file. Of course some scholar should have written a paper about this already… I just haven’t gotten around to searching the literature.

By the way, here’s something annoying. This picture on the Wikipedia article about De Divina Proportione purports to come from that book:

Again most of the rectangles don’t look very golden, even though it says “Divina Proportio” right on top. But here’s the big problem: I can’t find it in the online version of the book! Luca Luve, who spotted the online version for me in the first place, concurs.

Puzzle 3. Where is it really from?

Luca Pacioli

Luca Pacioli had many talents: besides books on art, geometry and mathematics, he also wrote the first textbook on double-entry bookkeeping! This portrait of him multitasking gives some clue as to how he accomplished so much. He seems to be somberly staring at a hollow glass cuboctahedron half-filled with water while simultaneously drawing something completely different and reading a book:

Note the compass and the regular dodecahedron. The identity of the other figure in the painting is uncertain, and so is that of the painter, though people tend to say it’s Jacopo de’ Barbari.

Piero della Francesca

This creepy painting shows three people calmly discussing something while Jesus is getting whipped in the background. It’s one of the first paintings to use mathematically defined rules of perspective, and it’s by Piero della Francesca, the guy whose pictures of polyhedra fill the third part of Pacioli’s De Divina Proportione.

Piero della Francesca seems like an interesting guy: a major artist who actually quit painting in the 1470’s to focus on the mathematics of perspective and polyhedra. If you want to know how to draw a perfect regular pentagon in perpective using straightedge and compass, he’s your guy.

Constructing the pentagon

I won’t tell you how to do it in perspective, but here’s how to construct a regular pentagon with straightedge and compass:

Just pay attention to how it starts. Say the radius of the circle is 1. We bisect it and get a segment of length 1/2, then consider a segment at right angles of length 1. But

so these are the sides of a right triangle whose hypotenuse has length √5/2, by the Pythagorean theorem!

Yes, I know I didn’t explain the whole construction… just the start. But the golden ratio is √5/2 + 1/2, so we’ve clearly on the right track. If you’re ever stuck on a desert island with nothing to do but lots of sand and some branches, you can figure out the rest yourself.

Or if you’ve got the internet on your desert island, read this:

• Pentagon, Wikipedia.

But here’s the easy way to make a regular pentagon: just tie a simple overhand knot in a strip of paper!

The pentagon-decagon-hexagon identity

The most bizarre fact in Euclid’s Elements is Proposition XIII.10. Take a circle and inscribe a regular pentagon, a regular hexagon, and a regular decagon. Take the edges of these shapes, and use them as the sides of a triangle. Then this is a right triangle!

How did anyone notice this??? It’s long been suspected that this fact first came up in studying the icosahedron. But nobody gave a proof using the icosahedron until I posed this as a challenge and Greg Egan took it up. The hard part is showing that the two right triangles here are congruent:

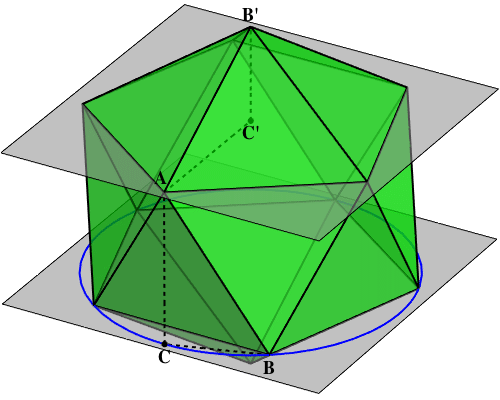
Then AB is the side of the pentagon, BC is the side of the decagon and AC’ is the radius of the circle itself, which is the side of the hexagon!

For details, see:

• John Baez, This Week’s Finds in Mathematical Physics (Week 283).

and

• Pentagon-decagon-hexagon identity, nLab.

The octahedron and icosahedron

Platonic solids are cool. A regular octahedron has 12 edges. A regular icosahedron has 12 vertices. Irrelevant coincidence? No! If you cleverly put a dot on each edge of the regular octahedron, you get the vertices of a regular icosahedron! But it doesn’t work if you put the dot right in the middle of the edge—you have to subdivide the edge in the exactly correct ratio. Which ratio? The golden ratio!

This picture comes from R. W. Gray.

According to Coxeter’s marvelous book Regular Polytopes, this fact goes back at least to an 1873 paper by a fellow named Schönemann.

Puzzle 4. What do you get if you put each dot precisely in the center of the edge?

The heptagon

The golden ratio Φ is great, but maybe it’s time to move on? The regular pentagon’s diagonal is Φ times its edge, and a little geometry shows the ratio of 1 to Φ equals the ratio of Φ to Φ+1. What about the regular heptagon? Here we get two numbers, ρ and σ, which satisfy four equations, written as ratios below! So, for example, the ratio of 1 to ρ equals the ratio of ρ to 1+σ, and so on.

For more see:

• Peter Steinbach, Golden fields: a case for the heptagon, Mathematics Magazine 70 (Feb., 1997), 22-31.

He works out the theory for every regular polygon. So, it’s not that the fun stops after the pentagon: it just gets more sophisticated!

Constructing the heptagon

You can’t use a straightedge and compass to construct a regular heptagon. But here’s a construction that seems to do just that!

If you watch carefully, the seeming paradox is explained. For more, see:

• Heptagon, Wikipedia.

Trisecting the angle

When I was a kid, my uncle wowed me by trisecting an angle. He wasn’t a crackpot: he was bending the usual rules! He marked two dots on the ruler, A and B below, whose distance equaled the radius of the circle, namely OB. Then the trick below makes φ one third of θ.

Drawing dots on your ruler is called neusis, and the ancient Greeks knew about it. You can also use it to double the cube and construct a regular heptagon—impossible with a compass and straightedge if you’re don’t draw dots on it. Oddly, it fell out of fashion. Maybe purity of method mattered more than solving lots of problems?

Nowadays we realize that if you only have a straightedge, you can only solve linear equations. Adding a compass to your toolkit lets you also take square roots, so you can solve quadratic equations. Adding neusis on top of that lets you take cube roots, which—together with the rest—lets you solve cubic equations. A fourth root is a square root of a square root, so you get those for free, and in fact you can even solve all quartic equations. But you can’t take fifth roots.

Puzzle 5. Did anyone ever build a mechanical gadget that lets you take fifth roots, or maybe even solve general quintics?