Last time I posed a puzzle: figure out the Coxeter diagrams of the Platonic solids.
When you do this, it’s hard to help noticing a cool fact: if you take a Platonic solid and draw a dot in the center of each face, these dots are the vertices of another Platonic solid, called its dual. And if we do this again, we get back the same Platonic solid that we started with! These two solids have very similar Coxeter diagrams.
For example, starting with the cube, we get the octahedron:
Starting with the octahedron, we get back the cube:
These pictures were made by Alan Goodman, and if you go to his webpage you can see how all 5 Platonic solids work, and you can download his free book, which includes a good elementary introduction to group theory:
• Alan Goodman, Algebra: Abstract and Concrete, SemiSimple Press, Iowa City, 2012.
When we take the dual of a Platonic solid, or any other polyhedron, we replace:
• each vertex by a face,
• each edge by an edge,
• each face by a vertex.
So, it should not be surprising that in the Coxeter diagram, which records information about vertices, edges and faces, we just switch the letters V and F.
Here’s the story in detail.
Tetrahedron
The tetrahedron is its own dual, and its Coxeter diagram
doesn’t change when we switch the letters V and F. Remember, this diagram means that the tetrahedron has:
• 3 vertices and 3 edges around each face,
• 3 edges and 3 faces around each vertex.
Cube and Octahedron
The dual of the cube is the octahedron, and vice versa. The Coxeter diagram of the cube is:
because the cube has:
• 4 vertices and 4 edges around each face,
• 3 edges and 3 faces around each vertex.
On the other hand, the Coxeter diagram of the octahedron is:
because it has:
• 3 vertices and 3 edges around each face,
• 4 edges and 4 faces around each vertex.
If we switch the letters V and F in one of these Coxeter diagrams, we get the other one… drawn backwards, but that doesn’t count in this game.
Dodecahedron and Icosahedron
The dual of the dodecahedron is the icosahedron, and vice versa. The Coxeter diagram of the dodecahedron is:
because it has:
• 5 vertices and 5 edges around each face,
• 3 edges and 3 faces around each vertex.
The Coxeter diagram of the icosahedron is:
because it has:
• 3 vertices and 3 edges around each face,
• 5 edges and 5 faces around each vertex.
Again, you can get from either of these two Coxeter diagrams to the other by switching V and F. That’s duality.
The numbers
But now let’s think a bit about a deeper pattern lurking around here.
Puzzle. If we take the Coxeter diagrams we’ve just seen:
V—3—E—4—F
V—3—E—3—F
V—4—E—3—F
V—5—E—3—F
and strip off everything but the numbers, we get these ordered pairs:
Why do these pairs and only these pairs give Platonic solids? I’ve listed them in a cute way just for fun, but that’s not the point.
There could be a number of perfectly correct ways to tackle this puzzle. But I have one in mind, so maybe I should give you a couple of clues to nudge you toward my way of thinking—though I’d be happy to hear other ways, too!
First, what about this pair?
Well, last time we looked at the corresponding Coxeter diagram:
and we saw it doesn’t come from a Platonic solid. Instead, it comes from this tiling of the plane:

What I’m looking for is an equation or something like that, which holds only for the pairs of numbers that give Platonic solids. And it should work for some good reason, not by coincidence!
One more clue. If your equation, or whatever it is, allows extra solutions like (2,n) or (n,2), don’t be discouraged! There are weird degenerate Platonic solids called hosohedra, with just two vertices, like this:
You can’t make the faces flat, but you can still draw it on a sphere, and in some ways that’s more important. The Coxeter diagram for this guy is:
And each hosohedron has a dual, called a dihedron, with just two faces, like this:
The Coxeter diagram for this is:
So, if your answer to the puzzle allows for hosohedra and dihedra, it’s not actually bad. As you proceed deeper and deeper into this subject, you realize more and more that hosohedra and dihedra are important, even though they’re not polyhedra in the usual sense.










So when we consider Coxeter diagrams of the form
V—3—E—n—F
for some natural number , we get tilings by equilateral triangles in which
, we get tilings by equilateral triangles in which  triangles meet at each vertex. For
triangles meet at each vertex. For 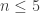 , these tilings live on the sphere, while for
, these tilings live on the sphere, while for 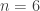 , it is a tiling of the plane. Since the number of triangles at each vertex determines the curvature, we should expect to get tilings of the hyperbolic plane for
, it is a tiling of the plane. Since the number of triangles at each vertex determines the curvature, we should expect to get tilings of the hyperbolic plane for  . I guess that this is the tiling associated to
. I guess that this is the tiling associated to 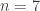 :
:
But what about ? Do those still exist? If so, are there any pictures around?
? Do those still exist? If so, are there any pictures around?
Now, I know that you either expect someone to bring this up here or you plan to explain this later in the series. If the latter is the case, feel free to delete this comment.
Tobias wrote:
Indeed, there are tilings of the hyperbolic plane with Coxeter diagrams
V—m—E—n—F
for all natural numbers m,n that are too big to give Platonic solids or tilings of the plane. Don Hatch has some great pictures of them. For example, here’s
V—8—E—3—F
drawn in white, and its dual
V—3—E—8—F
drawn in blue:
These hyperbolic regular tilings are deeply related to modular curves and thus number theory. The one you showed us, for example, is closely connected to Klein’s quartic curve and a bunch of number theory involving the number 7.
I’m actually happy to talk about these in the comments, because while I’m tempted to blog about them, doing so would vastly expand this series of posts. Almost everything I’ll do with Platonic solids and their truncations in 3, 4 and higher dimensions has a Euclidean analogue and a hyperbolic analogue! I hope to turn these blog posts into a semi-pop book someday, but if I’m not careful it will grow into an encyclopedia!
They always say that hyperbolic tilings are related to number theory. I figure that the combinatorial properties of tilings may be a fertile ground for number theory.
Then, what might be the modular curve analogue for a non-hyperbolic tiling? Or is it that only hyperbolic groups give “nontrivial” insight into number theory?
Sorry for the distraction, i just couldn’t resist.
Amazing pictures! I wish I knew more about the connections to number theory. By the way, I dimly remember seeing that picture on the main page of your website. Must have been a while ago…
One thing that really surprised me about hyperbolic surfaces is that you can maintain a rule such as “7 equilateral triangles at each vertex” and get wildly different topologies– the obvious one where it’s like a wrinkly plane or a lettuce leaf, or weid ones with lots of different intersecting tunnels. It’s sort of like how the rule “6 equilateral triangles at each vertex” gives either a flat plane or a cylinder (graphene or nanotube.)
Oh, I see you’ve gotten into this topic below.
I meant to include this picture, but apparently the html got stripped off:

Alas, only I can post pictures in comments—probably some sort of anti-spam measure. But I’m always glad to post them for people who comment here, as long as they’re useful. So I’ll fix this.
A regular n-gon can be decomposed into n identical isosceles triangles, with angles of 2π/n where they meet at the polygon’s centre. That means the other two angles in each triangle, which are identical, sum to π(1-2/n), and so that’s the interior angle between two edges of the polygon.
If we try to arrange m of these regular n-gons around a vertex of a polyhedron, the sum of all the angles between the edges must come to less than 2π. So we must have:
or
or a bit more symmetrically
For m=2 or n=2 that’s just . So we can have m=2, n = anything for the dihedra, and n=2, m = anything for the hosohedra. I’m not sure if people ever talk about the m=1 or n=1 cases.
. So we can have m=2, n = anything for the dihedra, and n=2, m = anything for the hosohedra. I’m not sure if people ever talk about the m=1 or n=1 cases.
Now, if we assume m > 2 and n > 2, then the inequality gives us:
So we only have a finite set of possibilities to try, with values for each variable ranging from 3 to 5. And the five pairs that satisfy the inequality are (3,3), (4,3), (5,3), (3,4) and (3,5).
Great! Since I like Egyptian fractions, which are sums of reciprocals of natural numbers, I like to start the way you did and then rewrite
as
or
In week182 of This Week’s Finds, I sketched how solutions of this equation give Dynkin diagrams of finite-dimensional simple Lie groups of types A, D and E. But these Lie groups actually correspond to unordered pairs m, n. So, these Lie groups correspond, in a sneaky way, to dual pairs of Platonic solids! More precisely:
• the exceptional Lie algebras E6, E7 and E8 correspond to the tetrahedron, the cube/octahedron, and the dodecahedron/icosahedron. These are the solutions with m and n are both > 2.
• the Lie algebras Dk = so(2k) correspond to the hosohedra/dihedra. These are the solutions where m or n are both ≥ 2 but at least one actually equals 2.
• the Lie algebras Ak = sl(k+1) correspond to the even more degenerate shapes you alluded to. These are the solutions where at least one of m or n equals 1.
This is called the ‘McKay correspondence’, and it runs very deep. Here’s a great introduction to it:
• Joris van Hoboken, Platonic solids, binary polyhedral groups, Kleinian singularities and Lie algebras of type A,D,E, Master’s Thesis, University of Amsterdam, 2002.
All this is the ‘spherical’ case of McKay correspondence. There’s also a lot to say about the ‘flat’ or ‘Euclidean’ case:
and the ‘hyperbolic’ case:
But for those, see week182!
I think you’ve got the third and the final displayed inequalities the wrong way round.
Whoops, you’re right. I fixed those mistakes. Glad to see you back in cyberspace, Simon!
Ah, ADE-ology. I suspect that in order to understand it, I’ll have to write a book on it. Or at least add several chapters to the manuscript for Universality and Renormalization I have slowly growing on my computer…
It should be enough to write a paper, or several blog articles.
I’m sure I can explain conformal field theory in one or maybe two blog posts! :-D
Oh, I was talking about the essence of ADE theory, not all its ramifications and applications…
I guess you’ve seen John McKay’s terse blast of information on this subject. It mainly serves to make you want to learn more.
But the same thing doesn’t work in four dimensions, right?
Later in this series we’ll certainly be using Coxeter diagrams to help classify Platonic solids in 4 dimensions. They’re also good for classifying ’tilings’ of 3d Euclidean space and 3d hyperbolic space by polyhedra. In case that mixture of 4’s and 3’s annoys you: these examples are actually all living in the same dimension, since a 4d Platonic solid is a special tiling of a 3-sphere by polyhedra. Spherical, planar and hyperbolic geometry always go hand in hand in mathematics.
But, understanding which Coxeter diagrams give which things isn’t simply a matter of taking sums of reciprocals. We’ll see, I guess!
Robert and Tobias are interested in how tilings of hyperbolic space are related to number theory, so let me say a bit about that. But I’m no expert on this huge and deep subject, so I hope some experts see this and say a bit more.
Platonic solids give tilings of the sphere by regular polygons. Regular tilings of the flat plane can be curled up to give tilings of a 1-holed torus by regular polygons. And regular tilings of the hyperbolic plane can be curled up to give tilings of tori with more holes by regular polygons. They’re probably all interesting for number theory, but I know a bit more about the third case.
For example, consider this drawing by Don Hatch:
The white lines show a tiling of the hyperbolic plane by regular heptagons, 3 meeting at each corner. So, the Coxeter diagram of this tiling (in my style of notation) is:
If we identify the heptagons with the same numbers here:
we get a tiling of a 3-holed torus by 24 heptagons, 3 meeting at each corner. Here’s a picture of it, drawn by Joe Christy:
The number 24 may seem arbitrary, but it’s not. There’s no way to tile the sphere, the 1-holed torus or the 2-holed torus by heptagons with 3 meeting at each corner, and any tiling of a 3-holed torus by heptagons with 3 meeting at each corner has to have 24 heptagons!
The result is actually a Riemann surface, Klein’s quartic curve, with the maximum number of symmetries for any 3-holed Riemann surface: 168 = 24 × 7. (This happens to be the number of days in a week, but that’s numerology, not number theory!)
But what probably matters more here is that we can think of this Riemann surface as the quotient of the hyperbolic plane by a discrete group. It’s
where is the hyperbolic plane, and
is the hyperbolic plane, and  is the group of 2 × 2 integer matrices with determinant 1 whose entries are all equal mod 7 to the corresponding entries of the identity matrix.
is the group of 2 × 2 integer matrices with determinant 1 whose entries are all equal mod 7 to the corresponding entries of the identity matrix.
The group is an example of a modular group and the Klein quartic seen as
is an example of a modular group and the Klein quartic seen as  is an example of a modular curve.
is an example of a modular curve.
Thanks to the general theory surrounding modular curves, Klein’s quartic curve can be seen as parametrizing elliptic curves with extra structure—namely, a fixed isomorphism between their 7-torsion subgroup and .
.
Hmm, the jargon seems to be getting thick and I haven’t really gotten to the number theory yet—at least, not in any way that’s recognizable as number theory to the uninitiated! If I knew this stuff better I could get to the number theory more rapidly. But it’s time for lunch. So I’ll stop here and maybe continue later.
days -> hours
(The story I’ve always heard is that the Babylonians liked 24— along with 60 and 360—because it has a healthy complement of integer divisors, and 7 because it’s the cardinality of the set {Moon, Mercury, Venus, Sun, Mars, Jupiter, Saturn}.)
Whoops! I had ‘days’ on the brain because this is related to a famous theory for how the days of the week got their names.
The idea is that astrologers liked to list the planets in order of decreasing orbital period, counting the sun as having a period of one year, and the moon as period of one month:
Saturn (29 years)
Jupiter (12 years)
Mars (687 days)
Sun (365 days)
Venus (224 days)
Mercury (88 days)
Moon (29.5 days)
For the purposes of astrology they wanted to assign a planet to each hour of each day of the week. To do this, they assigned Saturn to the first hour of the first day, Jupiter to the second hour of the first day, and so on, cycling through the list of planets over and over, until each of the 24 × 7 = 168 hours was assigned a planet. Each day was then named after the first hour in that day. Since 24 mod 7 equals 3, this amounts to taking the above list and cycling around it, reading off every third planet:
Saturn (Saturday)
Sun (Sunday)
Moon (Monday)
Mars (Tuesday)
Mercury (Wednesday)
Jupiter (Thursday)
Venus (Friday)
And that’s how they got listed in this order! At least, this is what the Roman historian Dion Cassius (AD 150-235) claims. Nobody knows for sure.
John wrote:
Well, let me just say one more thing! You can use Klein’s quartic curve to give a proof that Fermat’s Last Theorem holds for the exponent 7: there are no integer solutions of
with all three variables nonzero. (This is equivalent to other more familiar statements of Fermat’s Last Theorem for exponent 7.)
You can see the proof here:
• Noam Elkies, The Klein quartic in number theory.
Briefly, the idea is to start by noticing that the 3-holed torus I was discussing is isomorphic, as a Riemann surface, to the space of solutions of Klein’s quartic equation
modulo rescaling by a constant factor. Then, you use some wizardry to show that the only integer solutions of the above equation are those where at least two of the variables vanish. Then, you notice that an integer solution of
gives an integer solution of
by letting
since then
This is just one of many examples of how number theory gets related to tilings of hyperbolic space, and not at all the most profound, but it’s cute.
Your example doesn’t look very scary to me. That’s nice. Next time i’m lost in the jargon i’ll try and imagine klein’s quartic rolling over the hyperbolic plane. I can now see how spheres are limited and why a cylinder is a bit too plain for this kind of fun. Thanks for the insight, oh and for the link to the Congruence Groups.
Well, I sort of changed course midstream, switching from my intended goal to something I find easier to understand. If I’d kept marching boldly ahead, I would have said something like this (but longer, and maybe more helpful, though maybe less):
Since Klein’s quartic curve is a curled-up piece of the hyperbolic plane, it’s called a ‘modular curve’. Modular curves can be seen as parametrizing families of elliptic curves (roughly speaking, tori) equipped with extra structure.
This is a nice big story already. However, it then takes a weird turn and gets much more intense.
There’s another weirder relation between modular curves and elliptic curves. Sometimes an elliptic curve can be covered by a modular curve using a so-called ‘branched cover’. There’s a big theorem called the modularity theorem which says (very roughly) that all elliptic curves defined by equations using just rational numbers can be covered in this way by modular curves.
And this theorem implies Fermat’s Last Theorem!
So, as usual in number theory, the flashy easy-to-explain result follows as a corollary from something that’s harder to explain, but ultimately more interesting and more connected to geometry and symmetry.
The proof of the modularity theorem is not easy: Andrew Wiles and a grad student of his proved enough of it to get Fermat’s Last Theorem, and other good mathematicians finished off the job.
Instead of reading about that, it’s a lot less stressful to start with:
• Tim Silverman, Pictures of Modular Curves (Part I), n-Category Caf&eeacute;, 10 October 2006.
and read all 11 parts. You’ll get a deeper understanding of creatures like
as shown here:
John explained:
That’s weird: a modular curve, equipped with some additional structure defining the ‘branched quotient’ and this torsion subgroup iso, becomes itself a *point* in a modular curve! (In general, I suppose that this second curve is in general different from the first.)
Tobias wrote:
Yes, the modularity theorem is weirdly self-referential. I’ve always been puzzled why everyone explaining this stuff doesn’t mention that.
It’s even more amusing that this self-referential result is what it took to prove something seemingly ‘concrete’ like Fermat’s Last Theorem. As it happened, Gerard Frey suggested that a counterexample to Fermat’s Last Theorem
would give an elliptic curve
that couldn’t be covered by a modular one. This was later proved by Jean-Pierre Serre and Kenneth Ribet. And that made it clear what had do be done to prove Fermat’s Last Theorem: prove the modularity theorem, or at least enough of it to cover this case.
Nice posting! I think I see where you’re heading with this. The {3,4} pairs are called Schläfli symbols, and I imagine the 4-dimensional case is coming next. Lounesto does a good job in Ch.6 of his book, Clifford Algebras and Spinors, of taking you on a whirlwind tour of 3-d and 4-d ‘Platonic’ solids. And for a great exposition of the McKay Correspondence check out these notes by Qi Phillip on lectures given by M. Khovanov at Columbia a few years ago, http://www.math.columbia.edu/~khovanov/finite/QiYou1.pdf
Just thought I’d provide some references for those itching to learn more, the fun stuff for the McKay Correspondence comes from considering the relation between the angles of triangles on the platonic solids and the areas of spherical triangles obtained upon central projecting out from the center of the solid.
Those notes by Qi Phillip are very nice—thanks! I wish they’d been around when I was just learning this stuff! And his handwriting, if that’s what is, looks like it’s typed in a special font.
In response to a puzzle last time, Chris Namaste has worked out the Coxeter diagrams of all the regular tilings of the plane:
V—4—E—4—F
V—3—E—6—F
V—6—E—3—F
The square tiling is self-dual; the other two are dual to each other.
These tilings correspond to the solutions of
where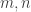 are positive integers.
are positive integers.
Greg Egan solved today’s puzzle here, but there’s another slightly different solution nobody has mentioned yet. This involves an equation instead of an inequality.
Suppose are trying to classify all the Platonic solids. We’re looking for ways to tile the surface of a sphere with regular -gons, with
-gons, with  meeting at each vertex. Suppose there are a total of
meeting at each vertex. Suppose there are a total of  vertices,
vertices,  edges, and
edges, and  faces. Since the Euler characteristic of the sphere is 2, we have
faces. Since the Euler characteristic of the sphere is 2, we have
Since each face has edges but 2 faces meet along each edge, we have
edges but 2 faces meet along each edge, we have
Since each vertex has edges meeting it but each edge meets 2 vertices, we also have
edges meeting it but each edge meets 2 vertices, we also have
Putting these equations together we get
or
Of course this implies the inequality we’ve already seen:
A priori the equation is stronger than the inequality, but it just happens to be equivalent, at least when
Whenever a sum of two reciprocals of two numbers like this exceeds 1/2, it exceeds 1/2 by a reciprocal of a number like this! And this number is the number of edges of your Platonic solid…
… or hosohedron, or dihedron.
For example
gives the cube, but in fact
so the cube has 12 edges! Simple but pretty stuff.
[…] couple series of posts from John Baez: Symmetry and the four dimension one, two, three, four. The Mathematics of Biodiversity eight-part […]