Hexagonal Tiling Honeycomb

This picture by Roice Nelson shows a remarkable structure: the hexagonal tiling honeycomb.

What is it? Roughly speaking, a honeycomb is a way of filling 3d space with polyhedra. The most symmetrical honeycombs are the ‘regular’ ones. For any honeycomb, we define a flag to be a chosen vertex lying on a chosen edge lying on a chosen face lying on a chosen polyhedron. A honeycomb is regular if its geometrical symmetries act transitively on flags.

The most familiar regular honeycomb is the usual way of filling Euclidean space with cubes. This cubic honeycomb is denoted by the symbol {4,3,4}, because a square has 4 edges, 3 squares meet at each corner of a cube, and 4 cubes meet along each edge of this honeycomb. We can also define regular honeycombs in hyperbolic space. For example, the order-5 cubic honeycomb is a hyperbolic honeycomb denoted {4,3,5}, since 5 cubes meet along each edge:

Coxeter showed there are 15 regular hyperbolic honeycombs. The hexagonal tiling honeycomb is one of these. But it does not contain polyhedra of the usual sort! Instead, it contains flat Euclidean planes embedded in hyperbolic space, each plane containing the vertices of infinitely many regular hexagons. You can think of such a sheet of hexagons as a generalized polyhedron with infinitely many faces. You can see a bunch of such sheets in the picture:

The symbol for the hexagonal tiling honeycomb is {6,3,3}, because a hexagon has 6 edges, 3 hexagons meet at each corner in a plane tiled by regular hexagons, and 3 such planes meet along each edge of this honeycomb. You can see that too if you look carefully.

A flat Euclidean plane in hyperbolic space is called a horosphere. Here’s a picture of a horosphere tiled with regular hexagons, yet again drawn by Roice:

Unlike the previous pictures, which are views from inside hyperbolic space, this uses the Poincaré ball model of hyperbolic space. As you can see here, a horosphere is a limiting case of a sphere in hyperbolic space, where one point of the sphere has become a ‘point at infinity’.

Be careful. A horosphere is intrinsically flat, so if you draw regular hexagons on it their internal angles are

2\pi/3 = 120^\circ

as usual in Euclidean geometry. But a horosphere is not ‘totally geodesic’: straight lines in the horosphere are not geodesics in hyperbolic space! Thus, a hexagon in hyperbolic space with the same vertices as one of the hexagons in the horosphere actually bulges out from the horosphere a bit — and its internal angles are less than 2\pi/3: they are

\arccos\left(-\frac{1}{3}\right) \approx 109.47^\circ

This angle may be familar if you’ve studied tetrahedra. That’s because each vertex lies at the center of a regular tetrahedron, with its four nearest neighbors forming the tetrahedron’s corners.

It’s really these hexagons in hyperbolic space that are faces of the hexagonal tiling honeycomb, not those tiling the horospheres, though perhaps you can barely see the difference. This can be quite confusing until you think about a simpler example, like the difference between a cube in Euclidean 3-space and a cube drawn on a sphere in Euclidean space.

Connection to special relativity

There’s an interesting connection between hyperbolic space, special relativity, and 2×2 matrices. You see, in special relativity, Minkowski spacetime is \mathbb{R}^4 equipped with the nondegenerate bilinear form

(t,x,y,z) \cdot (t',x',y',z') = t t' - x x' - y y' - z z

usually called the Minkowski metric. Hyperbolic space sits inside Minowski spacetime as the hyperboloid of points \mathbf{x} = (t,x,y,z) with \mathbf{x} \cdot \mathbf{x} = 1 and t > 0. But we can also think of Minkowski spacetime as the space \mathfrak{h}_2(\mathbb{C}) of 2×2 hermitian matrices, using the fact that every such matrix is of the form

A = \left( \begin{array}{cc} t + z & x - i y \\ x + i y & t - z \end{array} \right)

and

\det(A) = t^2 - x^2 - y^2 - z^2

In these terms, the future cone in Minkowski spacetime is the cone of positive definite hermitian matrices:

\left\{A \in \mathfrak{h}_2(\mathbb{C}) \, \vert \, \det A > 0, \, \mathrm{tr}(A) > 0 \right\}

Sitting inside this we have the hyperboloid

\mathcal{H} = \left\{A \in \mathfrak{h}_2(\mathbb{C}) \, \vert \, \det A = 1, \, \mathrm{tr}(A) > 0 \right\}

which is none other than hyperbolic space!

Connection to the Eisenstein integers

Since the hexagonal tiling honeycomb lives inside hyperbolic space, which in turn lives inside Minkowski spacetime, we should be able to describe the hexagonal tiling honeycomb as sitting inside Minkowski spacetime. But how?

Back in 2022, James Dolan and I conjectured such a description, which takes advantage of the picture of Minkowski spacetime in terms of 2×2 matrices. And this April, working on Mathstodon, Greg Egan and I proved this conjecture!

I’ll just describe the basic idea here, and refer you elsewhere for details.

The Eisenstein integers \mathbb{E} are the complex numbers of the form

a + b \omega

where a and b are integers and \omega = \exp(2 \pi i/3) is a cube root of 1. The Eisenstein integers are closed under addition, subtraction and multiplication, and they form a lattice in the complex numbers:

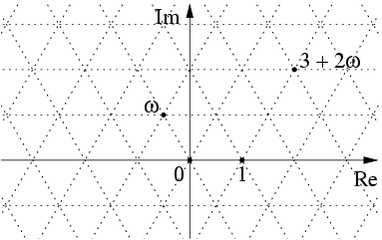
Similarly, the set \mathfrak{h}_2(\mathbb{E}) of 2×2 hermitian matrices with Eisenstein integer entries gives a lattice in Minkowski spacetime, since we can describe Minkowski spacetime as \mathfrak{h}_2(\mathbb{C}).

Here’s the conjecture:

Conjecture. The points in the lattice \mathfrak{h}_2(\mathbb{E}) that lie on the hyperboloid \mathcal{H} are the centers of hexagons in a hexagonal tiling honeycomb.

Using known results, it’s relatively easy to show that there’s a hexagonal tiling honeycomb whose hexagon centers are all points in \mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H}. The hard part is showing that every point in \mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H} is a hexagon center. Points in \mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H} are the same as 4-tuples of integers obeying an inequality (the \mathrm{tr}(A) > 0 condition) and a quadratic equation (the \det(A) = 1 condition). So, we’re trying to show that all 4-tuples obeying those constraints follow a very regular pattern.

Here are two proofs of the conjecture:

• John Baez, Line bundles on complex tori (part 5), The n-Category Café, April 30, 2024.

Greg Egan and I came up with the first proof. The basic idea was to assume there’s a point in \mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H} that’s not a hexagon center, choose one as close as possible to the identity matrix, and then construct an even closer one, getting a contradiction. Shortly thereafter, someone on Mastodon by the name of Mist came up with a second proof, similar in strategy but different in detail. This increased my confidence in the result.

What’s next?

Something very similar should be true for another regular hyperbolic honeycomb, the square tiling honeycomb:


Here instead of the Eisenstein integers we should use the Gaussian integers, \mathbb{G}, consisting of all complex numbers

a + b i

where a and b are integers.

Conjecture. The points in the lattice \mathfrak{h}_2(\mathbb{G}) that lie on the hyperboloid \mathcal{H} are the centers of squares in a square tiling honeycomb.

I’m also very interested in how these results connect to algebraic geometry! I explained this in some detail here:

• Line bundles on complex tori (part 4), The n-Category Café, April 26, 2024.

Briefly, the hexagon centers in the hexagonal tiling honeycomb correspond to principal polarizations of the abelian variety \mathbb{C}^2/\mathbb{E}^2. These are concepts that algebraic geometers know and love. Similarly, if the conjecture above is true, the square centers in the square tiling honeycomb will correspond to principal polarizations of the abelian variety \mathbb{C}^2/\mathbb{G}^2. But I’m especially interested in interpreting the other features of these honeycombs — not just the hexagon and square centers — using ideas from algebraic geometry.

This entry was posted on Saturday, May 4th, 2024 at 3:47 pm and is filed under mathematics. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

2 Responses to Hexagonal Tiling Honeycomb

  1. Victor V Albert says:
    4 May, 2024 at 5:18 pm

    Was just working on tilings this morning when I saw this. Congrats on the cute result.

    FWIW There’s a quantum error-correcting code definable on 4-valent 4-colorable tilings, which AFAIK have not been classified. https://errorcorrectionzoo.org/c/3d_color

    Reply
  2. John Baez says:
    5 May, 2024 at 8:45 am

    Over on Mastodon, Mist proved the new conjecture!

    The proof strategy I used before also works for the Gaussian lattice and square tiling honeycomb. Here’s an outline:

    Using the same notation as before for hermitian matrices, where the matrix [[a+b, c + di], [c – di, a – b]] is viewed as a vector (a, b, c, d), and using the negative of the Minkowski form, namely -a^2 + b^2 + c^2 + d^2, I choose vectors
    e_1 = (0, 0, 0, -1)
    e_2 = (0, 0, -1, 1) / sqrt(2)
    e_3 = (1/2, 1/2, 1, 0)
    e_4 = (0, -1, 0, 0)
    and check that they have the correct pairwise inner products to be a root system for the Dynkin diagram
    O–(4)–O–(4)–O—-O
    which corresponds to the square tiling honeycomb, as stated here: https://en.wikipedia.org/wiki/Square_tiling_honeycomb

    The first vertex of the Dynkin diagram is circled, meaning that the vertices of the squares in the tiling correspond to the extremal ray of the fundamental chamber which lies opposite to the facet defined by e_1. The shape of the fundamental chamber implies that the centers of the squares correspond to the extremal ray of the fundamental chamber which lies opposite to the facet defined by e_3. We can check that this extremal ray points in the direction of (1, 0, 0, 0), i.e. towards the identity matrix.

    To check that the Gaussian lattice is invariant under the simple reflections (and therefore contains the set of square centers), we let v be any element of the Gaussian lattice and consider the reflection
    v \mapsto v – 2 <v, e_i> e_i.
    For e_1, e_3, e_4, the inner product <v, e_i> is an integer, and e_i itself belongs to the Gaussian lattice, so the image lies in the Gaussian lattice. For e_2, the inner product <v, e_2> is 1/sqrt(2) times something in the Gaussian lattice, and the claim follows from the fact that sqrt(2) e_2 lies in the Gaussian lattice.

    To check that every norm-1 element of the Gaussian lattice is a square center, use the same strategy as before. The null vector n = (1, 1, 0, 0) again is an extremal ray of the fundamental chamber, and one can show that every norm-1 element v of the Gaussian lattice which lies in the (closed) fundamental chamber satisfies <v, n> = 1, i.e. it lies on the horosphere defined by this same equation. Again, this horosphere can be explicitly described as the set of points ((c^2 + d^2)/2 + 1, (c^2 + d^2)/2, c, d), and such a point is an element of the Gaussian lattice if and only if c and d are both integers. We can again check that the reflections e_1, e_2, e_3 generate a group which acts transitively on the 2D lattice of such pairs (c, d), so every norm-1 element of the Gaussian lattice is conjugate to (1, 0, 0, 0), as desired.

    Remark: The easiest way to figure out what e_1, e_2, e_3, e_4 have to be is to first figure out the points on the horosphere = 1, figure out how the simple reflections for e_1, e_2, e_3 must act on those points, and then look at the difference between each point and its image to find vectors parallel to e_1, e_2, e_3.

    Reply

You can use Markdown or HTML in your comments. You can also use LaTeX, like this: $latex E = m c^2 $. The word 'latex' comes right after the first dollar sign, with a space after it.

This site uses Akismet to reduce spam. Learn how your comment data is processed.