guest post by Tim van Beek
Fried on Mercury
Is it possible to fly to Mercury in a spaceship without being fried?
If you think it should be possible to do a simple back-on-the-envelope calculation that answers this question, you’re right! And NASA has already done it:

This is interesting for astronauts—but it’s interesting for a first estimation of the climate of planets, too. In particular, for the Earth. In this post, I would like to talk about how this estimate is done and what it means for climate science.
The Simplest Possible Model
How do physicists model a farm? They say: “First, let’s assume that all cows are spherical with homogeneous milk distribution”. – Anonymous
Theoretical physicists have a knack for creating the simplest possible model for very complicated systems and still have some measure of success with it. This is no different when the system is the whole climate of the earth:
The back-on-the-envelope calculation mentioned above has a name; people call it a ‘zero-dimensional energy balance model‘.
Surprisingly, the story of energy balance models starts with a prominent figure in physics and one of the most important discoveries of 20th century physics: Max Planck and ‘black body radiation’.
Black Body Radiation
Matter emits electromagnetic radiation—at least the matter that we know best. Physicists have also postulated the existence of matter out in space that does not radiate at all, called ‘dark matter’, but that doesn’t need to concern us here. ![]()
Around 1900, the German physicist Max Planck set out to solve an important problem of thermodynamics: to calculate the amount of radiation emitted by matter based on first principles.
To solve the problem, Planck made a couple of simplifying assumptions about the kind of matter he would think of. These assumptions characterize what is known in physics as a perfect ‘black body’.
A black body is an object that perfectly absorbs and therefore also perfectly emits all electromagnetic radiation at all frequencies. Real bodies don’t have this property; instead, they absorb radiation at certain frequencies better than others, and some not at all. But there are materials that do come rather close to a black body. Usually one adds another assumption to the characterization of an ideal black body: namely, that the radiation is independent of the direction.
When the black body has a certain temperature , it will emit electromagnetic radiation, so it will send out a certain amount of energy per second for every square meter of surface area. We will call this the energy flux and denote this as
. The SI unit for
is
: that is, watts per square meter. Here the watt is a unit of energy per time.
This electromagnetic radiation comes in different wavelengths. So, can ask how much energy flux our black body emits per change in wavelength. This depends on the wavelength. We will call this the monochromatic energy flux . The SI unit for
is
, where
stands for micrometer: a millionth of a meter, which is a unit of wavelength. We call
the ‘monochromatic’ energy flux because it gives a number for any fixed wavelength
. When we integrate the monochromatic energy flux over all wavelengths, we get the energy flux
.
For the ideal black body, it turned out to be possible for Max Planck to calculate the monochromatic energy flux , but to his surprise, Planck had to introduce in addition the assumption that energy comes in quanta. This turned out to be the birth of quantum mechanics!
Understanding Thermodynamics: The Planck Distribution
His result is called the Planck distribution:
Here I have written and
for two constants. These can be calculated in terms of fundamental constants of physics. But for us this does not matter now. What matters is what the function looks like as a function of the wavelength
for the temperature of the Sun and the Earth.
As usual, Wikipedia has a great page about this:
• Black body radiation, Wikipedia.
The following picture shows the energy flux as a function of the wavelength, for different temperatures:

The Earth radiates roughly like the 300 kelvin curve and the Sun like the 5800 kelvin curve. You may notice that the maximum of the Sun’s radiation is at the wavelengths that are visible to human eyes.
Real surfaces are a little bit different than the ideal black body:

As we can see, the real surface emits less radiation than the ideal black body. This is not a coincidence: the black body is by definition the body that generates the highest energy flux at a fixed temperature.
A simple way to take this into account is to talk about a grey body, which is a body that has the same monochromatic energy flux as the black body, but reduced by a constant factor, the emissivity.
It is possible to integrate the black body radiation over all wavelengths, to get the relation between temperature and energy flux
. The answer is surprisingly simple:
This is called the Stefan-Boltzmann law, and the constant is called the Stefan-Boltzmann constant. Using this formula, we can assign to every energy flux
a black body temperature
, which is the temperature that an ideal black body would need to have to emit
.
Energy Balance of Planets
A planet like Earth gets energy from the Sun and loses energy by radiating to space. Since the Earth sits in empty space, these two processes are the only relevant ones that describe the energy flow.

The radiation emitted by the Sun results at the distance of earth to an energy flux of about 1370 watts per square meter. We need to account for the fact, however, that the Earth receives energy from the Sun on one half of the globe only, on the area of a circle with the radius of the Earth, but radiates from the whole surface of the whole sphere. This means that the average outbound energy flux is actually of the inbound energy flux. (The question if there is some deeper reason for this simple relation was posed as a geometry puzzle here on Azimuth.)
So, now we are in a position to check if NASA got it right!
The Stefan-Boltzmann constant has a value of
which results in a black body temperature of about 279 kelvin, which is about 6 °C:
That is not bad for a first approximation! The next step is to take into account the ‘albedo’ of the Earth. The albedo is the fraction of radiation that is instantly reflected without being absorbed. The albedo of a surface does depend on the material of the surface, and in particular on the wavelength of the radiation, of course. But in a first approximation for the average albedo of earth we can take:
This means that 30% of the radiation is instantly reflected and only 70% contributes to heating earth. When we take this into account by multiplying the left side of the previous equation by 0.7, we get a black body temperature of 255 kelvin, which is -18 °C.
Note that the emissivity factor for grey bodies does not change the equation, because it works both ways: the absorption of the incoming radiation is reduced by the same factor as the emitted radiation.
The average temperature of earth is actually estimated to be some 33 kelvin higher, that is about +15 °C. This should not be a surprise: after all, 70% of the planet is covered by liquid water! This is an indication that the average temperature is most probably not below the freezing point of water.
The albedo depends a lot on the material: for example, it is almost 1 for fresh snow. This is one reason people wear sunglasses for winter sports, even though the winter sun is considerably dimmer than the summer sun in high latitudes.

Since a higher albedo results in a lower temperature for the Earth, you may wonder what happens when there is more snow and ice? This results in a lower absorption, which leads to less heat, which results in even more snow and ice. This is an example of positive feedback, which is a reaction that strengthens the process that caused the reaction. There is a theory that something like this happened to the Earth about 600 million years ago. The scenario is aptly called Snowball Earth. This theory is based on geological evidence that at that time there was a glaciation that reached the equator! And it works the other way around, too.
Since a higher temperature leads to a higher radiation and therefore to cooling, and a lower temperature leads to a lower radiation, according to the Planck distribution, there is always a negative feedback present in the climate system of the earth. This is dubbed the Planck feedback and has already been mentioned in week 302 of “This Weeks Finds” here on Azimuth.
Now, the only variable that a zero dimensional energy balance model calculates is the average temperature of earth. But does it even make sense to talk about the “average” temperature of the whole planet?
The Role of the Atmosphere and Rotation
It is always possible to “put a planet into a box”, calculate the inbound energy flux, and compute from this a black body temperature —given that the inbound energy per second is equal to the outgoing energy per second, which is the condition of thermodynamic equilibrium for this system. We will always be able to calculate this temperature
, but of course there may be very strange things going on inside the box, that make it nonsense to talk about an average temperature. As far as we know, one side of the planet may be burning and the other side may be freezing, for example.
For planets with slow rotation and no atmosphere, this actually happens! This applies to Mercury and the moon of the Earth, for example. In the case of Earth itself, most of the heat energy is stored in the oceans and it spins rather fast. This means that it is not completely implausible to talk about a ‘mean surface air temperature’. But it could be interesting to take into account the different energy input at different latitudes! Models that do that are called ‘one-dimensional’ energy balance models. And we should of course take a closer look at the heat and mass transfer processes of the earth. But since this post is already rather long, I’ll skip that for now.
The Case of the Missing 33 Kelvins
The simple back-of-the-envelope calculation of the simplest possible climate model shows that there is a difference of roughly 33 kelvin between the black body temperature and the mean surface temperature on earth.
There is an explanation for this difference; I bet that you have already heard of it! But I’ll postpone that one for another post.
If you would like to learn more about climate models, you should check out this book:
• Kendal McGuffie and Ann Henderson-Sellers, A Climate Modelling Primer, 3rd edition, Wiley, New York, 2005.
Whenever I wrote “NASA” I was actually referring to this paper:
• Albert J. Juhasz, An analysis and procedure for determining space environmental sink temperatures with selected computational results, NASA/TM—2001-210063, 2001.
The pictures of black body radiation are taken from this book:
• Frank P. Incropera, David P. DeWitt, Theodore L. Bergman, Adrienne S. Lavine, Fundamentals of Heat and Mass Transfer, 6th edition, Wiley, New York, 2006.
Being Cool on Mercury
I want to paint it black. — The Rolling Stones
Last but not least: you can fly to Mercury without getting fried… but you have to paint your spaceship white in order to get a higher albedo.
Really? Well, it depends on the albedo of the whitest paint you can find: the one that reflects the Sun’s energy flux the most.
So, here’s a puzzle: what’s the whitest paint you can find? What’s its albedo? And how hot would a spaceship with this paint get, if it were in Mercury’s orbit?

I think the simple and conclusive answer would be provided by the radiant temperature of the earth, as observed from space. I’m rather puzzled why the public discussion never seems to drift toward that. As its decline would provide rather simple and definitive evidence of earth warming and it’s been steadily declining. There are also some interesting large convective hot spots, since that seems to be how most of the heat that does get to the upper atmosphere travels. Why wouldn’t scientists trying to convey the science just start with that!? It’s so simple and direct. We all seem to spend so much time with discussions that wander in endless circles, though.
The World Map of radiant temperature to space is followed by a chart of “temperature anomalies” (change per year) for the lower stratosphere, that I think roughly corresponds to the external radiant temperature of the earth. It’s a start for someone who has time to follow it up perhaps.
http://www.synapse9.com/issues/PlanetaryRadTemp.jpg
http://www.synapse9.com/issues/StratosphereTempsglobal-jan-dec-pg.gif
To your challenge to mathematicians about saving the earth, you need to get down to basics which you already tacitly assume. Because we live the life spans of “mayflies” in a sense, most people cannot understand what all the environmental concerns are. They’re still thinking like people when the earth’s population was 1 billion. You guys need to come up with easy to understand, non-patronizing, explanations of nonlinear growth and exponential growth. This is the key to getting the urgency across to all. After that, you work on negative and positive feedback, like Donella Meadows book “Thinking in Systems.” It’s an educational problem that could be solved through our mass media systems. Maybe even simple animated memes. Having worked as an illustrator with a lifelong passion for science, I can design such shows, then you have to pay to get them across to the millions of Americans. This is the biggest key to get public acceptance, and no media corporations are doing it: If processes are too slow to perceive in a lifetime then it always will be, and therefore out of sight, out of mind.
David Fricks
So you say:
I think that the assumption that the body does not either generate or store any more energy should be stated explicitly, otherwise one might not understand why perfect absorption has to imply perfect emission.
Also, i would guess that the physical mechanism behind the emission is that when atoms vibrate and bounce onto each other electrons absorb kinetic energy and jump orbitals, and when they go back to their original orbitals they emit a photon that goes away. Is that right ? or there is something more fundamental going on ?
That is if we had a neutron star, or something without electrons, (a black hole), would it still have a back body radiation ? I guess so, but then, another mechanism for sending out photons would have to be in place, right ?
Giampiero said:
You are hitting the nail on the head, but a different nail than you think :-)
The black body radiation refers to a free quantum gas of photons in thermodynamical equillibrium, that is at a well defined temperature T. Where the necessary energy comes from is not specified; it is not part of the definition of a black body.
In the simplest possible Gedankenexperimentalaufbau, you may simply think of the body being coupled to a heat bath, having an arbitrary heat capacity greater than zero, and infinitetly fast heat transportation, so that every part of the 3D body is always at the same constant temperature T.
But: You are right that this is an assumption that is implicitly made in the energy balance model of the earth. Not only is the earth supposed to emit and absorb as a black body, it is also assumed that there is infinite heat conductivity so that there is a well defined, constant, surface temperature. This assumption has been criticized in the past. But to address this criticism, we have to move beyond the zero dimensional energy balance model of this post. If I get to write a follow up, I’ll provide a little bit more detail about this.
Molecules have different degrees of freedom:
* Electrons can climb the orbital ladder,
* atoms in a molecule can vibrate,
* the molecule itself can rotate.
All of these degrees of freedom have discrete energy states, so that you don’t get a continuous spectrum, especially if you have a small set of different molecules in the mix. This will become important when we look at the radiative properties of the atmosphere. You get a better approximation to black body radiation with solids that have an approximately continuous spectrum of states for electrons “roaming freely”, like in metals.
Ugh, that’s getting over my head. Does somebody know what neutron stars do?
Hawking radiation of black holes can be explained in a metaphorical way by vacuum fluctuations of quantum fields, with one part of the fluctuation behind, and one in front of the event horizion. That’s a different mechanism for sure! But it’s also a theory without experimental evidence so far.
When you say:
do you mean that the object that best approximates, or represents (in theory at least) the “black body” is a free quantum gas of photons ? That’s not the easiest thing to imagine, given that photons move at the speed of light, but i can go on with it.
So if you have a single molecule that just rotates, (it moves therefore i would say that it has a temperature) , but nothing else happens, does it emit photons ? If yes how ?
I know that electrons that go back down the orbital ladder emit photons, but that’s as much as i know, so I am not sure how to associate the last 2 degrees of freedom that you mention with photons being emitted by the body.
Hence my question about what happens if you have something in the body that does not have any electrons, like just a bunch of neutrons.
What if you don’t have anything at all, like just an empty box of space ? or an hypothetically perfect mirror ? or something that is half mirror and half empty ? Any radiation absorbed by the box is also perfectly emitted, so can these examples count as a black bodies too ?
Sorry if these are weird questions, and i realize that are not relevant to the problem at hand (climate modeling), but i figure that while we are talking about this subject i could just try to understand these things a little bit more.
Giampiero wrote:
It’s not as weird as it sounds. If you heat up a box, the inside will be full of radiation, whose spectrum will depend on the temperature of the box’s walls. If the box is evacuated, all it will contain is a gas of photons. If this gas is in thermal equilibrium at a certain temperature, the distribution of radiation of different wavelengths will be the Planck distribution.
In practice, this will work best if the walls of the box are as black as possible: that is, have a high emissivity which is close to frequency-independent. Thermo Gauge Instruments Inc. has a nice advertisement for their Precision Blackbodies, which shows the entrance aperture of a windowless graphite tube blackbody furnace at 2000 °C:
They claim:
Ha, that’s an interesting advertisement. That comes in handy; I had planned to talk about a little bit how one measures infrared radiation: The instruments are gauged against black body radiation input, so there’s a possible use for the black body radiators.
Giampiero said:
That’s basically a question for quantum field theory; as long as matter interacts with the electromagnetic field, it can create and absorb photons (of certain wavelengths).
Now we are getting beyond the borders of established language: In “empty space” you still have quantum fields. When you have a black hole, this is in theory still empty space, because the black hole solutions of general relativity like the Schwarzschild solution are solutions to the vacuum Einstein field equations: There is no matter present! But according to Hawking the presence of an event horizon leads to radiation, the Hawking radiation.
A mirror reflects the incoming radiation, that is not what a black body does. If you send in gamma rays, you get out gamma rays. If you send gamma rays to a black body, you get back black body radiation dependent on the temperature of the black body. If it has the temperature of the Earth, you’ll get back infrared radiation mostly.
Ok thanks guys for the explanations, mostly i wasn’t sure about what exactly was meant by “absorption”. But i think i get it now. This in fact pretty much nails it:
Therefore if you don’t send any radiation to a black body that has a temperature T it emits energy at different wavelengths until the temperature decreases to zero, which takes forever.
Right. At temperature T it emits energy at a rate proportional to T4, so it cools off and its temperature asymptotically approaches absolute zero.
Giampiero wrote:
In my previous reply I forget to mention that the answer to this question is no.
A free quantum gas of photons is not at all like a black body!
Why not? Simple: a black body is an ideal substance that’s as black as possible. A free quantum gas of photons is just a bunch of light. Light isn’t black.
In other words: light is really bad at absorbing light, while a black body is an ideal substance that’s as good as possible at absorbing light.
To get a good approximation to a black body, use a chunk of charcoal. To get a much better one, take a large box, coat the inside with charcoal or black point, and poke a small hole in it. Since the hole is small, any radiation entering the hole is likely to bounce off the walls many times before it has a chance of escaping. Thus, it’s very likely to be absorbed.
For this reason, if you heat such a box, the radiation emitted will be a very good approximation to blackbody radiation.
There is an argument here which I’m omitting: namely, why a very black substance will emit radiation very close to blackbody radiation when heated. Briefly, the idea is that blackbody radiation is a gas of photons in thermal equilibrium. The light bouncing around in the box will come close to thermal equilibrium with box’s walls. So, it will be close to blackbody radiation.
And that is why a device like this can create a good approximation to blackbody radiation:
If you turned off the heat, the chance that a photon of visible light shot into the hole would get absorbed in the box is 99.5% (according to their advertisement).
It was an interesting post, but not the one that the title lead me to believe. When I saw ‘can we…’ the problem I expected to see addressed was how to provide adequate radiation shielding so that biological systems (ie us) could survive the journey without significant genetic damage. This is problematic even for sending living astronauts to Mars and back.
Even with unmanned flights, there are significant dealing with protecting the spaceships components from the number high energy particles passing by Mercury (They may be a small proportion of the total energy flux but they can be very destructive).
Planck’s model is actually very good. In constructing the
model all the information except the temperature was thrown away, but we still get pretty good fit to many observed phenomena.
Well, for instance, the interval ± 15K doesn’t allow for, e.g., molten rock, which we know is present in our geology…
Sorry, I don’t understand your point. Are you talking about the thing volcanoes still emit? Long ago there was indeed a time that the earth’s crust was not formed yet. But the mantle and nucleus of the earth are still much hotter than the surface, which has nothing to do with solar radiation as far as I know.
I too am confused about the point here. But I can imagine someone arguing that geothermal heat, not the greenhouse effect, is the reason the Earth is warmer than Tim’s simple calculation so far suggests.
Geothermal heat comes from radioactive decay of elements in the Earth. This provides some heat to the Earth’s surface. Could this help explain the missing 33 kelvin?
This is certainly worth thinking about. But, if you examine the Earth’s energy budget, you’ll see that geothermal heat provides just about 0.08 watts/m2 to the Earth’s surface. This is tiny compared to the 1370 watts/m2 that hits the top of the Earth’s atmosphere at full noon. It’s even tiny when we take the Earth’s albedo, its spherical shape, etc. into account.
So, geothermal heat is negligible for what we’re talking about now.
I was mostly musing on that anecdote about the poor professor who had to give a lecture in Lord Kelvin’s presence explaining why the latter was wrong to estimate that the Earth could be only a few hundred thousand years old, if not for some source of heat we hadn’t yet discovered, because otherwise the Earth should be a solid (or crumbly) rocky lump. I’m certainly not looking to be controversial about where those 33 degrees don’t go!
I think i am stating the obvious here, but this incidentally also means that the real average temperature of the whole box in which the earth is included is even (very slightly) higher than the temperature of the surface alone.
In other words you cannot make the case that the missing 33K are due to the fact that the interior is colder than the surface because if it was so then heat would flow the other way around.
On the other hand the common perception is that if you go down a few meters below the surface it actually gets colder, even in the night, but that cannot be true in average.
I’ve been very distracted by the quantum gravity conference I’ve been attending for the last week. But I can’t resist trying to solve Tim’s puzzle… and I’m appalled that nobody else has tried yet!
First, what are the whitest known things? According to Wikipedia article on high-reflection coatings:
However, even this ‘fairly broad wavelength range’ is not good enough for keeping our spaceship cool! We need to protect it from sunlight ranging from infrared to visible and maybe beyond. Visible light ranges from 4000 to 7000 angstroms or 400-700 nanometers in wavelength, which is already a much broader range than the ‘tens of nanometers’ mentioned above.
So, we’ll have to settle for something less reflective, but reflective over a broader range of wavelengths. I’m not sure what’s best. Titanium dioxide? Magnesium oxide? Or maybe a metal mirror? I’m having trouble finding information on the reflectivity of these as a function of wavelength. Help!
So, let me just suppose I have something that reflects 95% of light at all wavelengths. According to Tim’s picture, the solar energy flux at Mercury’s orbit is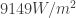 . As Tim explained, we must multiply this by 1/4 if our spaceship is a sphere. (As we saw in our earlier discussion of this issue, the same factor of 1/4 applies to any shape, as long as it’s tumbling erratically). We then multiply it by 0.05 if our spaceship reflects 95% of the radiation that hits it. This gives
. As Tim explained, we must multiply this by 1/4 if our spaceship is a sphere. (As we saw in our earlier discussion of this issue, the same factor of 1/4 applies to any shape, as long as it’s tumbling erratically). We then multiply it by 0.05 if our spaceship reflects 95% of the radiation that hits it. This gives
watts per square meter.
We could go on and work out the corresponding temperature using the Stefan-Boltzmann law. But even before doing this, we can see that our astronauts won’t ‘fry’.
Why not? Because even before taking into account the factor of 1/4, we get
watts per square meter, and this is much less than the 1370 watts per square meter of sunlight that hits the top of the Earth’s atmosphere at full noon!
So, a spacecraft that reflects 95% of all radiation will be cooler near Mercury than we are here on Earth!
I’ve been coming back to learn the answer as well. Thanks for tackling it.
It’s interesting that simple searches for best reflectance and emittance turn up pages of information on roof coatings — an indication that this question is important when trying to cut money spent on air conditioning.
Historically, NASA and others have used gold foil as a heat shield.
Suppose one drops that much Argon into the atmosphere, that surface pressure doubles (to 2 atm). How would surface temperature change?
This is a great question! I could really use some help here.
If we stick to the model of the blog post, the answer would of course be: No effect at all, because the overall energy balance does not change when we change something inside the box.
I hope to write a little bit about the effect of the atmosphere in a later post, so we’ll have the opportunity to come back to this question later, but it would also be great if someone could help me figure out the answer here and now.
When we assume that the atmosphere is in hydrostatic equillibrium, we can calculate the dry adiabatic lapse rate and see that it does not depend on the pressure. So this seems to imply that the temperature profile would not change. But I’d like to see a more elaborate explanation by an expert :-)
About your 33K puzzle, I had 2 guesses: geothermal energy and the greenhouse effect. John Baez claims it can’t be geothermal energy, so I’m guessing it’s the greenhouse effect.
Geothermal energy is one possibility; then there are fires that release energy; there is also the moon and the tides: The tides transfer potential gravitational energy of the moon to the earth, causing the moon to come closer and closer to earth . And there may be other possibilities.
But there are two problems: The process has to be steady, because the temperature difference is pretty stable, and it needs to have a huge impact, because heating earth by 33 kelvin requires a lot of energy. This rules out all of the processes I mention above. The “greenhouse effect” is of course a possibility that most people have probably heard of. But I don’t want to spoil the game :-)
Apropos nothing or perhaps bringing the discussion back to Earth. In World changing (Steffen) there is a note that states that if NYC could raise the albedo just a small amount it would have a dramatic positive effect on air quality, residential health and energy consumption (study by NYC Design Trust for Public Space).! So how can we paint NYC white?
How does a higher albedo lead to better air quality? (It will certainly lead to less air conditioning during the summer, which may have a positive influence on air quality indoors).
Vapour-deposited magnesium, overlaid with the mentioned layers of MgF2 and, what was the other thing, TiO2? probably are the best you can do. See figure 3, US patent 5022726.
Since you’re in space, you can do the vapour-depositing while under way. And just plain magnesium, no overlayers, is pretty good all by itself.
Any estimate of the albedo?
TiO2 (titanium dioxide) is indeed very white, apparently because of its high index of refraction.
Apparently people often add titanium dioxide to skim milk to make it look nicer! For some reason I don’t like this idea, even if it’s safe.
TiO2, ZrO2, and HfO2 are uniquely inert among oxides. Well, about even with corundum.
Reflection from many randomly oriented refracting crystals is a diffusion-like process, similar to the reflection of neutrons from a block of carbon. But specular reflection is what the patent is about. You can see a thumbnail of figure 3 at the bottom, with the albedo for the multilayer mirror, and the albedo is darn near 100 percent over quite a wide band.
I suspect, but do not know, that most car headlamp reflectors are using magnesium now-a-days. You’ll notice how bright they are, in terms of reflecting the landscape, even when the lamps are not on, next time you’re in a parking lot.
GRL wrote:
Does anyone know the albedo for this or any other coating that claims to be extremely reflective? “Darn near 100 percent” is too vague—since I’d like to calculate, just for fun, how close a spaceship covered with this stuff can get to the Sun without roasting the crew.
For keeping your spacecraft cool, you don’t want one of those “darn near 100% albedo” finishes. The problem is that you want a material that combines high albedo to sunshine with low albedo for thermal infrared. That way it reflects incoming light, but also radiates heat like a black (well, dark gray) body. Books on spacecraft design like tabulating the albedo and emissivity of various finishes (actually they tabulate the absorbance, which is one minus the albedo). Here, albedo is integrated over the solar spectrum, while the emissivity is measured for a thermal spectrum at the design temperature, usually near 300K. White paint has an albedo of around 80%, which is pretty good, but an emissivity of around 90%, which is what makes it so useful. Polished aluminum has an albedo of better than 90%, but a disastrous emissivity of only 4%. What you want for emissivity is not a polished surface, but a surface with bumps on the scale of the emitted radiation. In visible light, such a surface looks matte.
I’m getting these numbers from a table in “Space Mission Analysis and Design, 3rd edition” by Larson & Wertz. It’s on page 436. There’s a bigger table in “The Space Environment” by Tribble, but I can’t find my copy right now. There’s also a table on page iv of this space paint catalog which of course only covers paint from one company.
If you’re designing a spacecraft to get close to the Sun, you don’t paint it just one color, and you don’t use just one layer of insulation. The sunward side can be covered with “multilayer insulation”, which is basically layers of metal foil separated by vacuum. It gets as hot as heck because of its dreadful emissivity, but if you design it right, most of the heat gets radiated back toward the Sun instead of into the payload. And on the dark side of the spacecraft you put a matte black radiator.
–Carl Feynman
Thanks! All that is really cool—much more creative than the “white as possible paint all over” approach.
I guess it might make sense to look at NASA’s Messenger mission to Mercury and other real-world attempts to send satellites really close to the Sun. This satellite had a “large ceramic-cloth sunshade”.
Some questions that come to mind:
How hot did Messenger get?
What’s the closest a satellite has come to the Sun?
How how did it get? Was it cleverly painted?
John Baez writes,
Yes, one does want the shaded side to be emissive.
There’s another interesting approach, although as I recall it depends on human command of in-space resources that are of an astounding year to come: build a spaceship that has, per square metre of ventral area, as it skims solar spicules at perihelion, 20 or so cubic metres of liquid hydrogen.
Actually there is a pair of such approaches. In one, you transpire this hydrogen out ventral pores to keep the sunlit skin at a temperature that hot hydrogen-percolated tungsten is comfortable with. Or hydrogen-percolated ultrahyperstuff, if the year is really astounding. Because a freely falling ship that is skimming the sun’s surface goes 620 km/s, the time spent transpiring away 60+ MW/m^2 is short enough.
The second approach is to duct the hydrogen through ducts that are near under the surface, but do not communicate with it. Rather, they converge into an expansion nozzle that lets the heated hydrogen escape aft.
This is called an Oberth maneuver. A ship that drops from 1 A.U. down to sun-skim, cools itself thus, and drops up to 1 A.U again passes 1 A.U. at much more than solar system escape velocity.
Last time, when we talked about “putting the Earth in a box”, we saw that a simple back-of-the-envelope calculation of the energy balance and resulting black body temperature of the earth comes surprisingly close to the right answer.
But there was a gap […]
One of the big problems in science education and in simply discussing the issues regards how we argue the correctness of a mathematical argument. A case in point is the discussion of “Earth in a Box” equilibrium arguments taking place at Judith Curry’s Climate Etc blog right now.
One side argues for the 1370/4 flux ratio (the accepted view, and as derived by Tim here), and the other side argues for 1370/2 (the climate skeptic view). The skeptics are resolute in their defense of this factor, using arguments that a layman might just consider logical, largely because they use familiar concepts (i.e. night and day).
I find it a fascinating discussion because it points to how opposing camps develop and whether any resolution is actually possible.
Is there anything we can do about these kinds of fundamental differences in thinking? Or is this just about people believing what they want to believe to fit their preconceived notions? IMO, it is really a fascinating view of human behavior.
I’m completely baffled by the general acceptance that mean planetary temperature is influenced by its ‘albedo’ or, to use another term, reflectivity. This is utter nonsense, only those with a serious thermal physics deficiency could even begin to believe this; it goes well over half way to saying a planet’s temperature is a function of its colour
The principle involved is that planets only gain and lose energy through radiation, there is no wavelength or reflectivity factor that has any influence on the steady state temperature in such an arrangement.
All these calculations involving ‘planetary albedo’ influencing planetary temperature are an unscientific fairy story. The only effect of the albedo has is to make a small change in the rate of temperature change when other changes such as the orbital distance; insolation etc. that really do influence the (mean) temperature themselves change. There is no mechanism that allows an object with zero thermal divergence to have its temperature influenced by its emissivity.
What’s “thermal divergence”?
I’m glad you raised this issue, because it’s worth analyzing in detail.
Just to get things rolling, here’s an argument that people may enjoy dissecting:
Is this argument correct? Or if it’s wrong, is there a way to fix it and derive some other paradox that proves it’s “utter nonsense” to think that the temperature of a planet could be affected by its albedo?
Divergence is the classical vector interperetation. In this case it means there is no source of thermal energy in the volume. This corresponds well with the electrical case where the surface integral of the field of a volume is a measure of the charge contained in that volume.
The surface temperature of a planet that does not contain a heat source is entirely determined by incident radiation, its geometry and any energy transport means e.g. gas flow, conduction etc. available.
On a ‘whole planet’ basis, thus for global effects, this means the albedo plays no role in determining mean planetary temperature.
From geometrical considerations a planet is not evenly heated, thus the surface will have thermal gradients which, should there be any energy transport methods available e.g. fluid flow, these will strongly influence the surface temperature.
Geometrical considerationse, e.g. is the planet rotating or not, play an important role in determining surface temperature, what is frequently cited as the greenhouse effect is merely the excess local temperature observed during the daylight period when the Sun illuminates the surface; the same excess temperature is not seen during planetary night.
Dermod wrote:
Okay, that’s what you believe. Why do you believe it?
Do you believe that a white blanket and a black blanket lying next to each other in the sunlight, with the exact same geometry, should have the same temperature?
John, You nailed the question. These are the thought processes that I also want to understand.
Unless we can understand someone’s thought process, it becomes very difficult to argue effectively. It’s also why we spend so much time correcting homework assignments for someone with very muddled thoughts (and why TA’s exist :)
John wrote:
I’m a bit bummed that nobody wanted to tackle this puzzle. But I don’t want to leave it hanging around unsolved, so before I forget:
No, this argument is incorrect.
Since the Sun is providing a constant flow of free energy to the system, it does not count as a ‘perpetual motion machine’ if the system is able to extract work at a constant rate from the incoming sunshine.
Indeed, the fact that we can extract work from temperature differences arising from sunshine interacting differently with different objects is well-known: it’s the basis of concentrated solar power.
But more specifically, for this system:
The white rock has lower emissivity at visible frequencies than the black rock. If they have comparable emissivity at infrared frequencies, the black rock can have a higher temperature than the white one, as discussed here. We can thus build a device that extracts work from this temperature difference.
It’s also worth adding that while two objects in thermal equilibrium must have the same temperature, the rocks here are not in thermal equilibrium. Nor is the planet Earth. Nor, for that matter, is a covered pot of water with a flame underneath that creates convection cells like this:
There is a flow of free energy through these systems, so that even if they happen to be in a steady state, they are not in thermal equilibrium — so the fact that systems in thermal equilibrium must have uniform temperature does not apply.
If the Sun and Earth suddenly stopped having internal heat sources would they come to thermal equilibrium or do bodies have to physically touch each other to be in thermal equilibrium ?
If two bodies can exchange energy with each other, but not with the rest of the universe, they will come into thermal equilibrium.
The Sun and Earth can exchange energy by means of electromagnetic radiation (visible light, infrared, microwaves, etc.), but they can also exchange energy with the rest of the universe.
If you put them in an enormous perfectly mirrored box, and don’t let them hit the walls of the box , they would eventually reach thermal equilibrium with each other, and with the electromagnetic radiation in the box. This would happen sooner if you could magically remove their internal heat sources, but eventually even if you didn’t.
, they would eventually reach thermal equilibrium with each other, and with the electromagnetic radiation in the box. This would happen sooner if you could magically remove their internal heat sources, but eventually even if you didn’t.
In reality, it seems what will happen is this:
In 1.1 billion years, the Sun will become 10% brighter than it is today and start a runaway greenhouse effect leading to a complete loss of the Earth’s oceans.
In 3 billion years, the >Andromeda galaxy will collide with the Milky Way, shaking loose many planets in many solar systems, perhaps including ours.
In 3.5 billion years, the Sun will become 40% brighter than today, and conditions on Earth, if it’s still in its current orbit, will become like those on Venus today.
In 5.4 billion years, the Sun’s core will run out of hydrogen, and the Sun will enter its first red giant phase, becoming 1.6 times bigger and 2.2 times brighter than today.
In 6.5 billion years, the Sun will become a full-fledged red giant, 170 times bigger and 2400 times brighter than today.
In 6.7 billion years, the Sun will start fusing helium and shrink back down to being 10 times bigger and 40 times brighter than today.
In 6.8 billion years, the Sun will run out of helium and, too small to start fusing carbon and oxygen, it’ll enter a second red phase. It’ll become 180 times bigger and 3000 times brighter than today.
In 6.9 billion years, the Sun will start to pulsate every 100,000 years, ejecting more and more mass in each pulse, and finally throwing off all but the hot inner core, becoming a white dwarf. It will then gradually cool down for a long, long time.
(All this is assuming we don’t get our act together and do something.)
Hi Dermod,
sorry, but I don’t understand your objection well enough to be able to address it. The two basic mechanism we are talking about here are:
* reflection of incoming radiation at roughly the same wavelength, which corresponds to “elastic scattering of incoming photons”,
* absorption of incoming radiation, which turns incoming energy into “warmth”, then re-emitting the energy at very much lower frequencies.
The fraction of the first process in percent of incoming radiation flux is called albedo.
The steady state temperature is a function of the albedo (and therefore of the color), which you can test by putting a black and a white blanket in your garden in the sun.
So, when you say
…it goes well over half way to saying a planet’s temperature is a function of its colour…
Yes, but we’ll have to understand “color” with respect to all of the sun’s emission spectrum, not only to the part that is visible to humans.
I gave one attempt to formalize Dermod’s objection in an earlier comment. Here’s another:
Of course this can’t be the whole story, since a black blanket left in the sun really does get hotter than a white one. But it’s a good exercise to analyze this argument and see where the ‘flaw’ is.
And of course I don’t know what Dermod’s actual reasoning is, since he didn’t present it.
Tim, your analogy of a ‘blanket in the garden’ is not appropriate because the blanket has other means available to it for acquiring and losing energy. Sure a black object heats up more quickly than a less absorbant one, it also cools more quickly at night. Think of a vacuum flask, its internal temperature follows the ambient quite slowly but over a period the internal temperature is some kind of average of the ambient and that average must include the unilluminated time.
Dermod wrote:
We don’t need to worry about night here. If I leave a black and a white blanket in the sun, their temperatures stabilize in less than an hour. We can even imagine a controlled experiment where we put a black piece of cloth and a white one under a bright spotlight and let them sit there for a day, a week, or as long as you like. When their temperatures have stabilized, will their temperatures be equal, or different?
Which means are you referring to? Can we set up an experiment that eliminates those other means?
For example, if you’re worried about convection or conduction, we could do an experiment where are two pieces of cloth are hanging from wires in a vacuum and we shine a bright spotlight on them. When their temperatures have stabilized, will their temperatures be equal, or different?
“Don’t need to worry about night” Are you serious? This makes a joke of the whole matter. Because the intensity of the insolation varies periodically you must take this into account when calculation average temperature, don’t you see?
“Set up an experiment” To discover what? What part of what theory are you trying to verify?
Guys, it has been interesting talking to you but on what you write here we do not seem to have the same aim.
Have a nice day.
Dermod has conveyed the same arguments that I see elsewhere, specifically in this night versus day distinction. I don’t know, but it seems they miss the idea of a forcing function and the impulse response, i.e. the Green’s function solution to the boundary conditions. The details of the night / day dynamics really does not matter when we want to achieve a steady-state value, and as a sanity check we just apply the duty-cycle average flux.
I also see some people toss out the idea of non-linearities in the response function. I might be able to understand this if some sort of “pumping” occurred whereby the physical properties change during the periodic cycling. So with the blanket example, say the day-time temperature got hot enough that some structural transformation occurred in one of the blankets, changing the emissivity or some other property. In this case the duty-cycle averaging of heat absorption against the stationary properties would not apply.
The problem though is that they don’t really explain what the exact mechanism is, just that it is a daily “non-linearity”. I see them mention ice versus water, but is that it. So if the planet was covered with a thin layer of water and melting/freezing dynamics occurred every day, how much would this change the analysis?
Like I said, frustrating trying to figure out the thought process. What I also dislike is that someone may mistake my misunderstanding on what they are saying as some sort of general ignorance. That is, they will use the confusion to further muddy the waters — “See, he is as confused as they are!”
I looked at one of the papers by the day/night analysts, Joseph Postma, and I think I can reproduce it via a duty-cycle approach (remember that I am only trying to rationalize his approach so don’t blame me).
Say that the daily temperature, , goes as
, goes as
where oscillates about some value
oscillates about some value 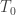 with a daily period. This models a day-to-day heating cycle.
with a daily period. This models a day-to-day heating cycle.
The SB law goes as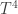 so that if we average this cyclic value over one day, then the radiation is increased to first order by
so that if we average this cyclic value over one day, then the radiation is increased to first order by  from the stable $T_0$ value. So according to Postma’s theory and what parameters he says are required, the
from the stable $T_0$ value. So according to Postma’s theory and what parameters he says are required, the 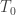 temperature is about 300K and the upper excursion is about 360K, so that
temperature is about 300K and the upper excursion is about 360K, so that 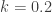 and the radiation increase is
and the radiation increase is 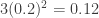 from the average.
from the average.
He says that the temperature excursions aren’t actually measurable but that they exist in some state obscured by going into “latent heat, evaporation, and convection in the macro case, and intramolecular degrees of freedom in the micro case”, in his words.
So this is the non-linear averaging of some instantaneous variation of the Stefan-Boltzmann law. The higher temperature excursions produce much higher radiation so that an overall higher equilibrium temperature is achieved.
He did this to show that green-house gases are not needed to show the missing 33 degree temperature shift. I don’t know what to make of this thinking, but there you go. I also don’t know if this applies exactly to Dermod’s thoughts.
This is Postma’s paper:
Click to access The_Model_Atmosphere.pdf
with a rebuttal here
http://www.skepticalscience.com/postma-disproved-the-greenhouse-effect.htm
Dermod wrote:
You claimed that the color of a planet has no effect on its temperature—or something like that. But a planet is a complicated thing, so I wanted to start by checking your opinion on a much simpler question. That’s why I asked:
You didn’t answer this question, but you said to Tim that:
So, I decided to simplify the situation even more, by focusing on a static situation. That’s why I asked:
You didn’t answer this question, but you said to Tim that:
So, I decided to simplify the situation even more, eliminating conduction and convection. That’s why I asked:
Again you didn’t answer this question.
I would appreciate answers to the 3 questions I’ve asked. Otherwise I can’t understand your views.
Hi Dermod,
John is not trying to do an oral undergraduate exam in thermodynamics with you, instead the three questions he asked are a useful way to try to understand where we agree and to identify the point where we may disagree. So it would be helpful if you answered them.
Dermod said:
If you have witnessed a night in a desert (smoking hot while the sun is up, freezing cold soon after sunset), you may have – like me – a somewhat misleading intuition about the role of day and night in the overall energy balance of the earth.
First note that we do not calculate an average temperature directly, rather we calculate the average radiation flux of the earth (and then assign a blackbody temperature to the average outgoing energy flux of longwave radiation).
The radiation flux emitted by earth does not depend strongly on night and day, the variations between the day and the night side are very small (sorry, I don’t have a good reference for this. If someone else has one, I would be grateful.)
Why is that? The reason for this is that
a) the oceans are the most important heat reservoir on earth, and they don’t cool noticably during the night (surface temperature does almost stay constant),
b) the atmosphere does also not vary fast enough to cool down considerably during nighttime.
The big exception is of course the boundary layer at the surface over land, especially if the air is dry. Since this is where we humans reside most of the time, most of us will have a wrong impression about night and day and the energy balance.
So, I don’t think that the most important correction to the 0-dimensional energy balance model would be taking night and day into account.
John, I am new to the editor here so I am getting my postings muddled!
Any ‘flaw’ to be found seems to come from geometrical considerations. Of course things get really hot in full sunlight but planets such as Mercury get really cold on the side facing away from the Sun, just like on the Moon. The Moon is a good example because its polar regions have hollows that never get sunlight, this is why water may be (is?) found there.
The case of a planet containing a heat source, e.g. the Earth with U238 and K40 in its crust, produces about 0.1W/m^2. With no other influence this would produce some tens of K at the surface. However, if you goldplated the planet, reducing its emissivity to about 0.05, then the surface temperature would rise considerably; if you put the whole planet in multilayer insulation it might get even hotter, depending entirely on how effective the insulation was.
Adding insulation would have no effect on the mean temperature due to the Sun.
Dermod said:
I would like to object.
Because (if correct) is tiny with respect to the solar heat flux $Q$, I suppose a first-order approximation of Planck’s law is reasonable and I obtain:
(if correct) is tiny with respect to the solar heat flux $Q$, I suppose a first-order approximation of Planck’s law is reasonable and I obtain:
“I suppose a first order approximation … is reasonable” – , a fourth order effect.
, a fourth order effect.
I am not really sure what you mean.
But to clarify “a first order approximation of Planck’s law”:
“I would expect something about 25mK”. Which is about 100th of CMB.
The Stefan Boltzmann gives about 40K for 100mW/m^2 with the Earth’s emissivity = 0.7 (albedo = 30%).
For a gold plated Earth (emissivity = 0.05) the average surface temp. would be about 78K.
“I would expect something about 25mK”
It seems the (I thought common) notation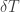 was not clear, but I am saying that
was not clear, but I am saying that 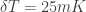 when
when  is around 300 K.
is around 300 K.
But I think understand where your confusion (in the remark above) comes from. When you wrote:
you really mean “no other influence”, while I thought you wanted to say “no other influence except the solar radiation “. To me it’s quite natural to consider solar radiation when we’re discussing to earth temperature.
Have a nice day/night too.
Thank you for your explanation. However the formulas you use do not reproduce in my browser, I get only the original coding which is mostly obscure to me.
Also, as installed on my machine, I cannot copy the text into my reply so I cannot provide an example; also the editor behaves in a most bizarre way, the text frequently disappearing entirely when trying to enter more; neither is there a preview facility; it really is most frustrating!
Regards.
Frederik: you seem to have forgotten that on WordPress blogs, equations in TeX are done as follows:
$latex E = mc^2 $
They have to start with a single dollar sign followed by ‘latex’ and then a space. As usual, the equation must end in a single dollar sign. No backslash before the ‘latex’! And no double dollar signs allowed!
So, the above produces
I’ve tried to fix your equations above.
There seems to be some confusion in this conversation. Here Dermod was talking about the temperature of a planet that was only heated by radioactivity:
Then Frederik started talking about the change in temperature caused by radioactive heat on a planet like the Earth, which is already heated by the Sun.
For Frederik’s question, a linearized approximation to the Stefan-Boltzmann law at T ∼ 300K is okay. But for Dermod’s original question, we really need to use the nonlinear Stefan-Boltzmann law, which says power radiated is proportional to T4.
The Stefan-Boltzmann law says that a blackbody radiates power per square meter equal to:
where the Stefan-Boltzmann constant is given by:
is given by:
Wikipedia says that radioactive heating of the Earth produces a power of roughly 0.1 W/m2. So, we get
or
or
where I’m including all the steps because I find it very easy to make calculational mistakes when writing equations on a blog!
This is consistent with Dermod’s estimate of “some tens of K at the surface”.
Ooof! What a relief. John your explanation is most welcome, both for the formulas and what I was trying to say.
I certainly agree, at first sight, with what Frederik is saying about the effect of radioactive heating on a planet already heated by the Sun. But, and this is the essential point I was making, a planet heated (and cooled) only by radiation from a star reaches an equilibrium temperature independent of its albedo, this is from the fundamental nature of the interaction of radiation with matter.
Because a planet is unevenly heated by the star the matter of where the equilibrium temperature is to be found is far from easy to decide but not really important in global considerations.
Climate on a gassy, fluid covered planet is determined by the distribution of heat due to the uneven insolation which, on Earth, is extremely complicated because the fluid flow over the surface is exceptionally unpredictable. On Venus, with its massive atmosphere, the surface temperature, equator to poles, is uniform to within a few degrees, even though it rotates so very slowly. Also there is very little surface wind on Venus, all the heat distribution takes place at about 50km altitude, whereas on Earth this is a surface effect called weather!
Back to your essential point then:
For me it is difficult to understand to understand how the albedo cannot affect the equilibrium temperature of the Earth.
Can it be that you believe that it is impossible to make an average of the local heat transfer equations (already formulated in terms of conduction, convection and radiation, let us not bother with QED etc) over the planet’s timescale, latitude and longitude to end up with an equation somewhat similar to
where Q is the average insolation, and effective albedo for the whole planet, and T the equilibrium temperature? Because this equation is what I have in mind when I decide the albedo does affect the equilibrium temperature.
and effective albedo for the whole planet, and T the equilibrium temperature? Because this equation is what I have in mind when I decide the albedo does affect the equilibrium temperature.
Here’s a calculation inspired by the Wikipedia article Temperature relation between a planet and its star.
Suppose a body is absorbing sunlight and re-radiating at infrared frequencies. Suppose the body is small and conductive enough that it has an almost uniform temperature . Simplifying the complicated absorption spectrum of real-world objects, suppose the body has albedo
. Simplifying the complicated absorption spectrum of real-world objects, suppose the body has albedo  for visible light, and
for visible light, and  for infrared radiation. So, the absorbed power is
for infrared radiation. So, the absorbed power is
where is the power of the sunlight hitting the body, and the power emitted is
is the power of the sunlight hitting the body, and the power emitted is
where is the body’s area and
is the body’s area and  is the Stefan-Boltzmann constant. In a steady state situation,
is the Stefan-Boltzmann constant. In a steady state situation,
so
so
The interesting thing is that if we assume
then the temperature doesn’t depend on the albedo : a higher albedo makes the body absorb more radiation but also emit more. What matters is not the albedo
: a higher albedo makes the body absorb more radiation but also emit more. What matters is not the albedo  by itself, but the ratio
by itself, but the ratio
A ‘greybody’ is a mythical object that has the same albedo at all frequencies. So, I believe that if an object meeting all the above conditions is also a greybody, its temperature after its come to equilibrium will be independent of its albedo.
If I’m wrong, someone please point out the mistake.
Needless to say, a planet deviates from some of the idealizing assumptions here.
Interesting point.
I think it would be more correct to say a greybody has constant emissivity.
Of course (see Atmosphere, Azimuth Library)
and absorptivity is what you use in the formulas above. I think that for your simplifying assumptions the absorptivity is the same as the albedo, but the definition for albedo in the literature is different (see the same page).
John wrote:
Frederik wrote:
Right, good point—I was imagining a frequency-dependent ‘albedo’, but people don’t seem to use that word that way.
Right. This is an example of an extremely general phenomenon called ‘reciprocity’:
Reciprocity is actually a lot more general than this passage indicates! It also includes the old principle ‘for every action there is an equal and opposite reaction’: if you push on me, I push on you.
More precisely,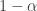 , which I called ‘one minus albedo’, would better be called ’emissivity’ or ‘absorbtivity’. For example, a completely black object has emissivity and absorbivity equal to 1, and albedo equal to 0.
, which I called ‘one minus albedo’, would better be called ’emissivity’ or ‘absorbtivity’. For example, a completely black object has emissivity and absorbivity equal to 1, and albedo equal to 0.
There are two relevant interactions between radiation and matter, there is absorption/emission and scattering. Absorption/emission are the thermal processes due to accelerating electric charge, you can examine these in various ways, the exchange of momentum between particles and photons, this is what Einstein did in his 1917 paper – he was concerned about the energy distribution of emitted photons. In ths case you can consider energy transfer as a collision (momentum exchange) broadly similar to kinetic theory.
The scattering interaction does not, at the thermal/optical energies we are concerned with, lead to a net change in momentum of the photon, it is merely redirected. There are of course many ways photons are scattered, coherent scattering can be a number of processes such as refraction and reflection, well described by the Fresnel equations.
The point is that the two processes, thermal and scattering, are mutually exclusive; the albedo of a planet is the scattering part, so while it is true that the albedo reduces the rate of energy that a body absorbs it also reduces the rate it can emit energy. For a substantial body this becomes equal at a temperature defined only by the the specific energy (the equivalent temperature) of the incident radiation. Thus it is quite impossible for a body with an albedo to emit ‘like a black body’ – which is at the heart of the calculations describing the greenhouse effect.
I say a substantial body because the photons from the Sun have energy related to the Sun’s temperature – 5780K, which is quite enough to split O2 molecules to form ozone and cause a number of other chemical reactions that would not otherwise take place at normal temperatures.
For substantial bodies the density of the Sun’s photons at a particular distance is reduced by the inverse square law and this is what defines the equilibrium temperature of any body in orbit around a star.
Just to understand your objections well, is your main point:
or
I tend to agree with the former remark, but I would like to point out John’s comment about the frequency-dependence. As an example (though not at the level of a planet) I propose: when walking in full sunlight it appears to matter to wear white or black clothes. I suppose they both colours act similarly in the IR region, but reflect visible light differently.
With respect to the latter remark: when calculating the earth’s temperature, one can take into account the emissivity (then the blackbody becomes a greybody) and in a better approximation, one can take into account a frequency-dependent emissivity. I don’t see any serious problems here. The blackbody is just a first approximation.
I am struggling mightily with this editor! This is supposed to be a response to Frederik’s recent remark about wearing black or white clothes in strong sunlight.
This is a question with nothing but counterintuitive responses! Are you aware that Touaregs wear black or dark clothing in the sun? The explanation I have heard is that the outer layers absorb the energy which is carried away by air currents.
In hot weather your body temperature is regulated to a considerable extent by evaporation and at first sight (how I hate this editor!- It reminds me of EDLIN) and one would imagine that the greater absorption of black material would place greater demands on evaporation. But one cannot ignore the powerful technique of multilayer insulation which the Touaregs seem to use. For them, to keep cool by evaporation would force a heavy dependence on water supply which is notoriously poor where they live.
As I say first intuitions are interesting but not necessarily reliable.
Dermod said:
The “heart of the greenhouse effect” is the effect of CO2 concentration in the atmosphere on downward longwave radiation and climate sensitivity. The effect on downward longwave radiation can both be calculated and measured independently of whether or not the blackbody approximation is a good or bad approximation for the emitted radiation flux of the Earth.
Dermod said:
You can write your text in an editor of your choice and copy&paste it on the blog, of course (but you have to be careful with latex, as John has explained).
Frederik, to reinforce the matter of ‘temperature being independent of albedo’ considerations of a ‘grey body’. Given sufficient pressure, the temperature of a gas is independent of it nature i.e. O2, CO2, N2 etc. There has to be sufficient pressure, otherwise gas is just a bunch of particles with no common energy.
But gases have extremely diverse emission/absorption characteristics, none the less their equilibrium temperature remains the same. The reason for this lies in the 2nd law of thermodynamics which explains that energy is transferred from hotter to colder places until the temperatures are the same, it doesn’t matter what the means of energy transfer is, radiation, conduction etc.
I don’t understand the relation of your latest point about gases with respect to the albedo. I thought that the albedo of a planet was primarily influenced by surface characteristics, not by the atmosphere (with an exception of clouds).
Your claim (as it appears to me) “because there exists a concept such as the ideal gas, the albedo of a planet would become irrelevant” I cannot believe (but perhaps I misunderstand your point).
Frederik, all gases scatter radiation, O2 scatters blue radiation giving us blue sky. All I am saying is that neither the emmissivity, the absorptivity nor the scattering coefficients have any influence on the equilibrium temperature reached by any material in an electromagnetic radiation field – it would be contrary to the 2nd law of thermodynamics.
Tim you say that the ‘Heart of the Greenhouse Effect’ is the effect of CO2 concentration on downward LW radiation. But the IPCC says the effect of this ‘downward’ radiation is to raise the surface temperature by 33K from about 255K to 288K. But this 255K surface temperature is based on a thermodynamically impossible assumption that the planet radiates like a ‘black body’ – it is a completely mistaken figure.
With regard to ‘downward longwave radiation’ there is no doubt at all that unsymmetrical molecules in the atmosphere can radiate in the infrared, you just have to look at infrared images of the planet to see this happening; but what is not possible is for this radiation to change the temperature on the surface or in the atmosphere.
The claims for this are so vague it makes it difficult to discuss; some authors say the lapse rate is changed by the radiation (in the right circumstances this happens e.g. in the stratosphere where UV has this effect).
Others (John Houghton of the IPCC) says that the effect comes about through the increase in the height of the emission layer due to the higher concentration of GHGs. A moment’s thought will reveal that this is pure fantasy and again the IR images of the emitting gases make it obvious that the radaiation does not come from a single layer but from the bulk of the gases and by far the greater part from water vapour.
Dermod wrote:
The Earth is not in thermal equilibrium, as noted here. Neither is the vastly simpler system I asked about earlier: a piece of cloth hanging on a string in a vacuum, with a spotlight shining on it. There’s a flow of free energy through them, thanks to the light that hits them. Such systems may reach a steady state, but this will typically not be thermal equilibrium.
So, to focus on the simpler example, it’s perfectly possible for the temperature of a piece of cloth hanging on a string in a vacuum, with a spotlight shining on it, to depend on the color of that cloth.
Indeed if we have a white piece of cloth and a black one, and they have comparable emissivities at infrared frequencies, the black one will have a higher temperature after it reaches a steady state.
This can be shown by calculations as sketched here, but it’s even better to do an experiment.
We’ll get a similar result for two pieces of cloth lying on a table under a spotlight: more heat will be carried off by conduction and convection, but the black one will still be hotter. And here the experiment is easy to do at home.
John, you claim ‘the Earth is not in thermal equilibrium’. I need clarification of this; systems that are not in thermal equilibrium have a temperature that is changing, while it is true that the surface of Earth does not have a steady temperature, to a first order, as a planet Earth has a constant temperature thust it is not exchanging energy with its environment, apart from the radioactive decay previously mentioned (to which we can add chemical changes such as plant growth and decay if you like). Now the argument for man made climate change (MMCC) appears, atleast in part, to be that the temperature of the planet is changing, in which case it must be exchanging energy with its environment. The argument is that gases with enhanced emissivitty in the IR part of the spectrum can do this i.e. changes in the planets colour can do this. If this colour change can do this it would be an effect outside all known thermodynamics and cause a revolution in every aspect of modern physics. I would welcome such a discovery but since it is claimed by a bunch of people who also claim the planet emits radiation ‘like a black body’, I personally need a little more light of the non-EM kind to be shed on the matter.
With regard to the ‘two rocks’ orbiting a star, I thought the response saying they both would be at the same temperature was conclusive.
You do not need two rocks, one rock part black and part white, you can try it in your back garden. If you do you will notice that, when the Sun shines the black one will get hotter than the white one and you can extract energy from the temperature difference. At night the effect is reversed, this is a backyard version of Maxwell’s demon and it works because there is a local disequilibrium caused by the change of insolation between day and night.
The exploitation of local disequilibrium is a useful way of extracting useful energy, wind, solar, tidal and hydroelectric are all popular ways of doing this, they all exploit local temperature differences. You could, if you were desperate, do this with your two orbiting rocks because they would not have uniform surface temperatures (equators hotter than poles etc.) whatever their colour but I imagine it would be rather costly to profit from the temperature difference of two such remote locations.
In connection with the ‘piece of cloth in a vacuum’. By definition (0th & 2nd laws of thermodynamics) objects with the same temperature are in thermal equilibrium.
As I observed before it is necessary to take into account geometrical matters. Just as a planet has to be considered as a whole to have an ‘average’ temperature, your blanket will have an ‘average’ temperature derived from the incident radiation.
However it is interesting to compare your blanket with a real system which could be a flat solar panel. There is a problem with flat solar panels, they work best when facing the Sun, in this attitude they are at their highest temperature, if they are for what ever reason, turned edge on to the Sun their temperature may drop to <70K in minutes through radiative cooling, this is not going to happen evenly accross the surface, giving rise to possibly destructive stress.
So what has happened to average temperature? It is a question of geometry, for a planet climatologists invariably consider a planet uniformly illuminated. But nothing in space is uniformly illuminated, only the smallest, highly conductive particles will have anything approaching a uniform temperature.
As far as your blanket is concerned you give insuficient information on its dimensions and orientation, if it is just 'hanging on a string in a vacuum' clearly there is no defining information available, that is why I wasn't really interested in considering it.
And your experiment 'easy to do at home'? I would find it exceptionally difficult to learn anything useful from so little description of the relevant parameters. One of the most impressive records of this kind of experiment was made by Benjamin Thompson in the 1790s, he took great care with his experiments, making sure they were repeatable and inventing the differential thermometer to detect temperaature changes of 1/100th of a degree R (Reamur). Thompson used materials with different emissivities and got results that made substantial contributions to the foundations modern physics. (He was the Thompson who determined the mechanical equivalent of heat using a blunt auger in a cannon.)
Dermod, Fascinating to read and to try to understand how you think.
I think the impasse may come down to a difference in understanding the distinctions between equilibrium and steady-state. You add in the phrase “local disequilibrium” which I would classify as a transient response caused by a stimulus.
The stimulus in this case is millions of years worth of buried carbon being released in the span of dozens of years as elevated concentrations of CO2 gas. This upsets the current steady-state and forces it into another steady-state that we are trying to quantify.
This may sound a bit pedantic, but we have to set up the premise so that we can apply your extensive engineering and science experience.
WebHubTelescope, you are wondering about the distinction between ‘equilibrium’ and ‘steady state’ that I am making.
It is my understanding that equilibrium arises when there is a strictly uniform temperature throughout the volume involved.
Because planets are illuminated from a star this doesn’t apply at all, the area facing the star is heated the most, the non-illuminated side is cooled. If the planet is not rotating this is not easy to analyse but a rotating planet like Earth has a fairly even heating and the planet can be given a figure called the average or equilibrium temp. This temperature is calculated by considering the planet emits as much radiation as it absorbed but this is not the uniform temperature of true equilibrium, such a condition would mean there is no internal heat transport (because ‘no temperature difference'(2nd law)).
This clearly doesn’t apply to many planets (but see my remarks about Venus). No planet/star system can ever fulfil all the condiitions of strict equilibrium because it relies on a star losing energy which is by definition not in equilibrium.
But the concept of equilibrium still has useful features. If the planets are at a steady distance from the star and only gain and lose energy by radiation from a star with a constant output of radiative energy, then the planet will have an average temperature, perhaps only measured (sometimes) at a few small places, will be unchanging.
I have already mentioned that real planets, being larger than a point, do not have uniform surface temperatures and this is largely what climate is about – how the excess heat arriving at the equator gets to the deficit areas towards the poles.
You may have noticed that I tend to go on but these matters are not simple!
I must thank you for raising a matter that had ecaped my attention here, it has caused me to think again on how to present these complicated matters.
Dermod wrote:
Yes, and I explained why: there’s a continual flow of free energy through this system, as low-entropy sunlight hits the Earth and gets re-radiated as higher-entropy infrared radiation. This continual flow of free energy powers the Earth’s weather systems (and also, by the way, life on this planet).
But even if we disregard the complications of weather—for example, by imaging an Earth with no atmosphere, more like the Moon—it’s crucial to note that planets are not in thermal equilibrium. They are not closed systems. Instead, they continually absorb radiation that comes from the Sun and turn it into a form of radiation that has more entropy. They are entropy-producing open systems.
No, that’s not always true. What’s always true is that systems that are in thermal equilibrium has a temperature that is not changing. But the converse is false, in general.
Namely, a system may be in a steady state without being in thermal equilibrium. As the Wikipedia article thermal equilibrium points out:
I gave a link to the Wikipedia article on ‘steady state’ when I first mentioned that concept, and here’s part of what that article says:
If we carefully studied a bathtub with the tap open but without the bottom plug, we’d notice that gravitational potential energy of the water flowing out the tap was being converted to kinetic energy as it fell into the tub, and then into heat as it hit the water in tub; this heat is then transferred to the environment. So, as in the example of a planet, we have an open system that is continually producing entropy. By contrast, a system in thermal equilibrium is not producing entropy.
It conclusively states your view of the matter, and that’s very helpful—thanks! But I’m sure that if the rocks have different emissivities for visible light (as they do, if one is white and the other is black), but approximately equal emissivities for infrared light, the black one will have a higher temperature. The relevant formulas, adapted from Wikipedia, are here.
I don’t know what ‘a backward version of Maxwell’s demon’ is supposed to mean; Maxwell’s demon is a mythical device that reduces entropy; every real system increases entropy and could thus be called a ‘backward version of Maxwell’s demon’.
More importantly, I don’t think ‘day and night’ are key here. I claim that you can take a black rock and a white rock, put them side-by-side under a powerful spotlight, let them sit there for a day, a week, a month, as long as you like, and the black one will be hotter—assuming they have comparable emissivities in the infrared, which should be easy to arrange without trying hard.
This sort of experiment—I proposed it earlier with two pieces of cloth—should be easy to do in your home. I think our readers can do it either with a thermometer, or simply by touching the pieces of cloth to feel which one is hotter. The difference should be substantial, so no high-precision equipment should be required.
John you claim “the Earth is not in equilibrium”. If this is true then the Earth is either gaining or losing energy and its temperature would be changing in sympathy.
Your explanation that ‘there is a… flow of energy through… the system’, makes me think – thermally speaking – isn’t that rather similar to the the planet being transparent?
Transparent objects also reach equilibrium and steady state temperatures even though they absorb/emit in only part of the radiation spectrum in a way that is quite comparable with reflective objects.
In either case the ‘through flowing energy’ to which you refer (energy doesn’t flow, that was the 18th Century caloric theory) by definition doesn’t influence the system’s temperature.
Only when, for whatever reason, the system temperature changes does the equilibrium in the energy transfer processes get unbalanced.
I suggest you check ‘Thermodynamic Systems’ in Wkipedia before deciding what a ‘closed’ thermodynamic system is – it is where “no mass may be transferred in or out of the system boundaries” but “heat and work can be exchanged across the boundary… “, this describes a planet very well.
It also describes a ‘steady state’ system where the energy arriving matches that leaving.
You claim a planet is ‘an open system’. continually producing entropy’? But surely ‘In open systems, matter may flow in and out of the system boundaries’. (Wikipedia – Thermodynamic systems) – a very small feature of planets.
Most planets are in a steady state, what the ‘greenhouse effect is claimed to do is to cause them to depart this steady state through minor variations in the surface characteristics – there is nothing in thermodynamics that would make this happen.
Sure, if the steady state changes; the planets orbit shifts, the temperature of the star changes or perhaps something eclipses the star, then there may be big changes on the way for planets surface.
But these are easily identifiable effects which fall well within the field of thermodynamics, they do not need planets to emit ‘like a black body’ or have minor changes in atmospheric composition.
By the way, a ‘backward version of Maxwell’s Demon is to be found in everyone’s ‘backyard’!
Dermod wrote:
No, that’s not true. I explained the difference between ‘thermal equilibrium’ and a mere ‘steady state’ here. I also explained why, even in the approximation where we treat the Earth as in a steady state, it’s not in thermal equilibrium. I also gave some other examples of systems that are in steady state, and thus are neither gaining nor losing entropy, yet are still not in thermal equilibrium.
The big difference is that the radiation emitted by a planet is very different from the radiation absorbed, while a transparent object doesn’t affect the radiation going through it. As I mentioned, the radiation emitted from a planet has considerably higher entropy than the radiation it absorbs.
Okay, thanks – I was using the terminology wrong. When I said the Earth was an ‘open system’, I should have said it was not an ‘isolated system’.
An isolated system will tend towards thermal equilibrium. But the Earth is not isolated, because it’s constantly receiving power from the Sun. I agree that it’s very close to being ‘closed’, meaning that there’s very little flow of matter in or out.
The most important point here is to understand why the Earth’s temperature can indeed depend on its albedo. For this a simple example is helpful—though not the end of the story. Two rocks touching each other, one white and one black, must be at the same temperature when they’re in thermal equilibrium. But if a bright light is shining on them, they probably won’t ever reach the same temperature! When their temperature stops changing, they will be in a steady state, but not thermal equilibrium.
John, you wrote “Two rocks touching each other, one white and one black, must be at the same temperature when they’re in thermal equilibrium. But if a bright light is shining on them, they probably won’t ever reach the same temperature!”
I can’t really argue about ‘probably won’t’ can I?
Seems I’m in the wrong place here. ‘Fraid I was looking for real physics.
Dermod wrote:
I explained here, with equations, the condition required for the two rocks to not reach the same temperature. Let me recap it for you:
Suppose a rock is absorbing visible light and re-radiating at infrared frequencies. Suppose it is small and conductive enough that it has an almost uniform temperature . Simplifying the complicated absorption spectrum of real-world objects, suppose the body has emissivity
. Simplifying the complicated absorption spectrum of real-world objects, suppose the body has emissivity  for visible light, and
for visible light, and  for infrared radiation. Then the absorbed power is
for infrared radiation. Then the absorbed power is
where is the power of the visible light hitting the body, and the power emitted is
is the power of the visible light hitting the body, and the power emitted is
where is the rock’s area and
is the rock’s area and  is the Stefan-Boltzmann constant. In steady state
is the Stefan-Boltzmann constant. In steady state
so
so
So, we see that two rocks must have the same value for
to reach the same temperature in steady state. If the rocks are at the same distance from the light source, the factor depends on the rock’s geometry. The factor
depends on the rock’s geometry. The factor  depends on its optical characteristics.
depends on its optical characteristics.
There’s a tiny chance that two randomly chosen rocks, one white and one black, will have exactly equal values for the ratio
But probably that will not be true. So probably they will reach different temperatures.
If you believe a black rock and a white rock under a spotlight necessarily have the same temperature when they reach a steady state, one experiment that gives the opposite result is enough to disprove your hypothesis. I think you should try the experiment, because it’s an easy experiment to do, and I believe your hypothesis will be disproved.
(By the way, I’ve deliberately simplified the math above by assuming the rocks absorb purely visible light and emit purely infrared light, and have one emissivity for all visible frequencies, and another
for all visible frequencies, and another  for all infrared frequencies. If you want, you can drop these simplifying assumptions. Then the formulas will involve integrals over all frequencies. I leave this as an exercise, but I’ll be glad to help if you get stuck. The basic conclusion—the two rocks probably won’t ever reach the same temperature—remains the same.)
for all infrared frequencies. If you want, you can drop these simplifying assumptions. Then the formulas will involve integrals over all frequencies. I leave this as an exercise, but I’ll be glad to help if you get stuck. The basic conclusion—the two rocks probably won’t ever reach the same temperature—remains the same.)
Gentlemen, I have noticed that you want me to discuss the relative heating of white and black blankets, presumably on the surface of some planet. I didn’t raise this matter and as far as I can see it has no direct connection with the temperature of objects orbiting a star.
Like all physics matters the exact circumstances and features of the matter under consideration are of supreme importance.
Some of you have remarked that I haven’t answered various points, I am sorry about that but it was my intention. If you are able to show a connection between the temperature of blankets etc. you refer to and that of a freely orbiting body I am happy to review it; I may add that I have experience in thermal control of spacecraft so most of the technical side does not come as a big surprise to me!
What do you think about the answer Carl Feynman gave to the puzzle posed at the end of the blog post?
Sorry that I cannot cite what Feynman says but with this editor I cannot even copy!
There are two principle problems with spacecraft, to maintain ‘suvivability’ temperatures in the face of wildly fluctuating solar input and to eliminate the need for fuel (or power) derived heat.
The gold coloured foil you see is multilayer insulation which has very low emissivity and absorptivity, this means that the enclosed volume is substantially free from external temperature influence such as sunlight an exposure to deep space.
Within the volume enclosed by the insulation the various components may be painted black to ensure the heat is distributed evenly; conduction has a role also if this fits in with the structural requirements. Some parts may be painted differently because spacecraft equipment uses energy captured by the solar panels and dissipated internally; this heat must be dissipated in a controlled way.
Thermal control of spacecraft is a challenging matter, check out Apollo 13 for the problems you can have.
Generally each space mission has a unique set of challenges that need to be solved in an original way.
Its interesting to note that the spacesuits used by astronauts may well be cooled by evaporating water into space.
Dermod wrote:
Sorry for the late answer: For some more information about the topic of downward longwave radiation see the follow up post “a quantum of warmth” here:
With regard to downward longwave radiation: It is possible to measure it, this has been done in a systematic way for some decades now, and the incoming energy flux is very relevant for the energy balance of the surface of the Earth.
There seems to be some discussion going on about wether or not downward longwave radiation “warmths” the surface: While the net energy flux is from the warmer surface towards the upper cooler atmosphere, downward longwave radiation leads to a higher steady state temperature on the surface.
Everyone who has witnessed cloudy versus cloudfree winter nights knows this from experience.
As an example I’ll cite a paper that is particularly interesting for me as a German :-)
* Albrecht Kessler, Lutz Jaeger: “Analysis of long time series of long-wave radiation fluxes above a pine forest” (online for free from the University of Freiburg, Germany, here).
I like it how the authors explain their experimental setup in this paper.
You will see that for the pine forest, the incoming longwave radiation energy flux from “greenhouse gases” can exceed the radiation flux that comes directly from the sun.
The “greenhouse effect” is about how higher concentrations of greenhouse gases can influence the downward longwave radiation flux and how this will change the climate of the Earth. Serious flaws in the zero dimensional energy balance model would of course have a serious influence on the analysis of the energy balance of the Earth, but the basic facts of the “greenhouse effect” understood as the influence of greenhouse gas concentrations on DLR would not be affected.
[…] Tim van Beek, Putting the Earth in a box, […]
I’ve shamelessly borrowed a lot of material from:
• Tim van Beek, Putting the Earth In a Box, Azimuth.