I try to focus on serious problems in this blog, mostly environmental issues and the attempt to develop ‘green mathematics’. But I seem unable to resist talking about random fun stuff now and then. For example, the Lebesgue universal covering problem. It’s not important, it’s just strange… but for some reason I feel a desire to talk about it.
For starters, let’s say the diameter of a region in the plane is the maximum distance between two points in this region. You all know what a circle of diameter 1 looks like. But an equilateral triangle with edges of length 1 also has diameter 1:
After all, two points in this triangle are farthest apart when they’re at two corners. And you’ll notice, if you think about it, that this triangle doesn’t fit inside a circle of diameter 1:
In 1914, the famous mathematician Henri Lebesgue sent a letter to a pal named Pál. And in this letter he asked: what’s the smallest possible region that contains every set in the plane with diameter 1?
He was actually more precise. The phrase “smallest possible” is vague, but Lebesgue wanted the set with the least possible area. The phrase “contains” is also vague, at least as I used it. I didn’t mean that our region should literally contain every set with diameter 1. Only the whole plane does that! I meant that we can translate, rotate and if necessary reflect any set with diameter 1 until it fits in our region. So a more precise statement is:
What is the smallest possible area of a region
in the plane such that every set of diameter 1 in the plane can be translated, rotated and/or reflected to fit inside
You see why math gets a reputation of being dry: sometimes when you make a simple question precise it gets longer.
Even this second version of the question is a bit wrong, since it’s presuming there exists a region with smallest possible area that does the job. Maybe you can do it with regions whose area gets smaller and smaller, closer and closer to some number, but you can’t do it with a region whose area equals that number! Also, the word ‘region’ is a bit vague. So if I were talking to a nitpicky mathematician, I might pose the puzzle this way:
What is the greatest lower bound of the measures of closed sets
such that every set
of diameter 1 can be translated, rotated and/or reflected to fit inside
Anyway, the reason this puzzle is famous is not that it gets dry when you state it precisely. It’s that it’s hard to solve!
It’s called Lebesgue’s universal covering problem. A region in the plane is called a universal covering if it does the job: any set in the plane of diameter 1 can fit inside it, in the sense I made precise.
Pál set out to find universal coverings, and in 1920 he wrote a paper on his results. He found a very nice one: a regular hexagon circumscribed around a circle of diameter 1. Do you see why you can fit the equilateral triangle with side length 1 inside this?
This hexagon has area
But in the same paper, Pál showed you could safely cut off two corners of this hexagon and get a smaller universal covering! This one has area
He guessed this solution was optimal.
However, in 1936, a guy named Sprague sliced two tiny pieces off Pál’s proposed solution and found a universal covering with area
Here’s the idea:
The big hexagon is Pál's original solution. He then inscribed a regular 12-sided polygon inside this, and showed that you can remove two of the corners, say 
Sprague conjectured that this is the best you can do.
But in 1975, Hansen showed you could slice off very tiny corners off Sprague’s solution, each of which reduces the area by just
I think this microscopic advance, more than anything else, convinced people that Lebesgue’s universal covering problem was fiendishly difficult. Victor Klee, in a parody of the usual optimistic prophecies people like to make, wrote that:
… progress on this question, which has been painfully slow in the past, may be even more painfully slow in the future.
Indeed, my whole interest in this problem is rather morbid. I don’t know any reason that it’s important. I don’t see it as connected to lots of other beautiful math. It just seems astoundingly hard compared to what you might initially think. I admire people who work on it in the same way I admire people who decide to ski across the Antarctic. It’s fun to read about—from the comfort of my living room, sitting by the fire—but I can’t imagine actually doing it!
In 1980, a guy named Duff did a lot better. All the universal coverings so far were convex subsets of the plane. But he considered nonconvex universal coverings and found one with area:
This changed the game a lot. If we only consider convex universal coverings, it’s possible to prove there’s one with the least possible area—though we don’t know what it is. But if we allow nonconvex ones, we don’t even know this. There could be solutions whose area gets smaller and smaller, approaching some nonzero value, but never reaching it.
So at this point, Lebesgue’s puzzle split in two: one for universal coverings, and one for convex universal coverings. I’ll only talk about the second one, since I don’t know of further progress on the first.
Remember how Hansen improved Sprague’s universal covering by chopping off two tiny pieces? In 1992 he went further. He again sliced two corners off Sprague’s solution. One, the same shape as before, reduced the area by just 
I believe this is the smallest convex universal covering known so far.
But there’s more to say. In 2005, Peter Brass and Mehrbod Sharifi came up with a nice lower bound. They showed any convex universal covering must have an area of least
They got this result by a rigorous computer-aided search for the smallest possible area of a convex set containing a circle, equilateral triangle and pentagon of diameter 1.
If you only want your convex set to contain a circle and equilateral triangle of diameter 1, you can get away with this:
This gives a lower bound of
But the pentagon doesn’t fit in this set! Here is a convex shape that also contains a pentagon of diameter 1, as found by Brass and Sharifi:
You’ll notice the triangle no longer has the same center as the circle!
To find this result, it was enough to keep the circle fixed, translate the triangle, and translate and rotate the pentagon. So, they searched through a 5-dimensional space, repeatedly computing the area of the convex hull of these three shapes to see how small they could make it. They considered 53,118,162 cases. Of these, 655,602 required further care—roughly speaking, they had to move the triangle and pentagon around slightly to see if they could make the area even smaller. They proved that they could not make it smaller than
They say they could have gotten a better result if they’d also included a fourth shape, but this was computationally infeasible, since it would take them from a 5-dimensional search space to an 8-dimensional one. It’s possible that one could tackle this using a distributed computing project where a lot of people contribute computer time, like they do in the search for huge prime numbers.
If you hear of more progress on this issue, please let me know! I hope that sometime—perhaps tomorrow, perhaps decades hence—someone will report good news.
References
Pál’s paper is here:
• Julius Pál, Ueber ein elementares Variationsproblem, Danske Mat.-Fys. Meddelelser III 2 (1920).
Sprague’s paper is here:
• R. Sprague, Über ein elementares Variationsproblem, Matematiska Tidsskrift Ser. B (1936), 96–99.
Hansen’s record-holding convex universal cover is here:
• H. Hansen, Small universal covers for sets of unit diameter, Geometriae Dedicata 42 (1992), 205–213.
It’s quite readable. This is where I got the picture of Pál’s solution and Sprague’s improvement.
The paper on the current best lower bound for convex universal coverings is also quite nice:
• Peter Brass and Mehrbod Sharifi, A lower bound for Lebesgue’s universal cover problem, International Journal of Computational Geometry & Applications 15 (2005), 537–544.
The picture of the equilateral triangle in the circle comes from an earlier paper, which got a lower bound of
by considering the circle and regular 
• Gy. Elekes, Generalized breadths, circular Cantor sets, and the least area UCC, Discrete & Computational Geometry 12 (1994), 439–449.
I have not yet managed to get ahold of Duff’s paper on the record-holding nonconvex universal covering:
• G. F. D. Duff, A smaller universal cover for sets of unit diameter, C. R. Math. Acad. Sci. 2 (1980), 37–42.
One interesting thing is that in 1963, Eggleston found a universal covering that’s minimal in the following sense: no subset of it is a universal covering. However, it doesn’t have the least possible area!
• H. G. Eggleston, Minimal universal covers in 
Later, Kovalev showed that any ‘minimal’ universal covering in this sense is a star domain:
• M. D. Kovalev, A minimal Lebesgue covering exists (Russian), Mat. Zametki 40 (1986), 401–406, 430.
This means there’s a point 
Azimuth 
This reminded me of a brief reference in the book “Littlewood’s Miscellany” to Kakeya’s problem: Find the region of least area in which a unit segment can turn continuously through 360 degrees.
It was long believed that the minimal region was a certain figure that (to me) looks similar to a 3-cusped hypocycloid, having area
But the story ends differently than for the Lesbesgue problem. In 1930 Littlewood’s friend Besicovitch proved that the area swept out could be less than any given positive epsilon. “As epsilon tends to 0 the movements of the segment become infinitely complicated and involve excursions towards infinity in all directions.”
That’s a great example of why we should talk about a ‘greatest lower bound’ instead of a ‘minimum’, unless we know the minimum is attained.
Besicovitch is also known for tackling the ‘worm problem’. Quoting Unsolved Problems in Geometry by Kroft, Falconer, and Guy:
• A.S. Besicovitch, On arcs that cannot be covered by an open equilateral triangle of side 1, Math Gazette 49 (1965) 286–288.
The Wikipedia article on Kakeya sets does show a line rotating in a deltoid, in exactly the fashion that arose in the discussion on rolling hypocycloids!
That article also mentions that Pál proved a result related to these sets.
Oh my gosh!
There are also some relations between Lebesgue’s covering problem and something else mentioned in the rolling hypocycloids discussion: Reuleaux triangles.
For starters, you can ask if there’s a maximal set of diameter 1 containing a triangle of diameter 1. The answer is clearly this:
This is an equilateral Reuleaux triangle.
Second, any Reuleaux triangle is a curve of constant width, meaning that the distance between two parallel lines just touching the curve is independent of their orientation. This is illustrated here:
But Lebesgue’s universal covering problem is equivalent to this: “what is the smallest area region containing a rotated or translated version of every curve of constant width 1?”
Third, Eggleston found a universal covering that’s the union of a disk of diameter 1 and a Reuleaux triangle of diameter 1. At least, that’s what this paper says:
• Peter Brass and Mehrbod Sharifi, A lower bound for Lebesgue’s universal cover problem, International Journal of Computational Geometry & Applications 15 (2005), 537–544.
but the details are fuzzy in their account, since they say this happens ‘when the triangle vertices are antipodal points of the circle’. You can’t have 3 antipodal points! Maybe they mean just two of the triangle’s vertices are antipodal points of the circle.
I guess I should get ahold of Eggleston’s paper…
It seems that the equivalent formulation you mentioned would be a good way to derive lower bounds, without searching in a big parameter space. Every curve of constant width would give a lower bound.
That’s true! Unfortunately, by the isoperimetric inequality and Barbier’s theorem, the curve of constant width with maximum area is already known: it’s the circle. So, the best lower bound we get via a naive application of this technique is the same as the lower bound we get by noticing that any universal covering must contain the circle of radius 1/2. Namely,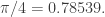
To go further we can try to find the region of least area that contains several curves of constant width 1, but then we’re back to Brass and Sharifi’s approach.
By the way, Barbier’s theorem is really cool.
I was not aware of Barbier’s theorem. It is a beautiful result; thanks for mentioning it!
Thanks for your reply!
John, how do you know that the universal covering problem for curves of diameter 1 is equivalent to that for curves of constant width 1?
You just have to show that every curve of diameter one is contained within a curve of constant width one.
Thanks Philip.
Thanks Greg! And per Wikipedia the area of a deltoid is twice that of the rolling circle (which is the same size as the inner circle above, whose area is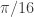
). So it seems the Littlewood figure is this deltoid (though the deltoid’s cusps look fatter to my eye – but what do I know, I thought John’s Reuleaux triangle was a Wankel engine rotor:-)
“You see why math gets a reputation of being dry: sometimes when you make a simple question precise it gets longer.”
Hmm, in “Cyrano de Bergerac” Roxane would not accept from Christian a short, plebeian declaration of love.
Should love get a reputation for being dry?
When unrequited, sure.
This looks like an ideal problem to investigate numerically using simulated annealing. Just take a large number of polygons of diameter one and use annealing to minimize the area of their union. It would not prove anything but it might tell you what the shape should look like. That might then inspire a proof or at least a conjecture. Has anyone tried that?
I don’t think anyone has tried that; I’ve been scouring the web for references to this problem and haven’t seen anything recent except what I discussed (and some less interesting references in those papers).
The problem, as you note, is that it wouldn’t prove anything. People seem to have been taking a proof-based approach to this puzzle. But your idea might help break the logjam! So I hope someone tries it.
One might start with a circle, a triangle, a pentagon and one other shape.
(I don’t know why people didn’t try a square, but maybe a square of diameter 1 fits inside the minimal-area union of a circle and triangle of diameter 1, in which case it doesn’t help.)
Any regular polygon with an even number of sides of diameter 1 will fit in a circle of diameter 1 (so only odd-sided REGULAR polygons of diameter one need be considered).
I’m not volunteering, but this shouldn’t be too hard – it seems to break down into 0) a way to specify the initial config, a) an algorithm to randomly perturb the current config, b) an algorithm to compute the convex hull of a config of polygons (actually, points) + circle, c) the simulated annealing algorithm itself, d) a simple gui.
Everything except b) looks quite easy, and I suspect b) is just a non-huge tweak to standard convex-hull-of-points algorithms (or perhaps you can rope in Brass and Sharifi:-)
I have it running as an applet, however I am not agreeing with the result of Brass and Sharifi. In the minimum I get that one side of the pentagon lines up with one side of the triangle so the angle they have as 61.045 is really 60 degrees. The minimum area is 0.8336185. I also find that sides line up if you add in more polygons so that the shape has a bilateral symmetry. I will post some results are pictures after some longer runs probably tomorrow.
The regular polygons are not the only shapes to consider. I can use the Reuleaux shapes too but will also have to add some irregular polygons. I should be able to do the original non-convex case aswell later.
So you really think you beat Brass and Sharifi, getting a convex hull area of only 0.8336185?
You didn’t beat them by much, but would be huge news (in the miniscule community of people who care about this problem) if Brass and Sharifi thought an angle was 61.045° when it should really be something nice like 60°.
Usually when I make a discovery that would be ‘huge news’, it’s wrong. So, if you give us the coordinates describing your best minimum-convex-hull-area configuration of width-1 circle, triangle and pentagon, a bunch of us check to see if you really beat Brass and Sharifi.
I don’t want to claim they are wrong. I am only claiming I got a different answer. My circle was a polygon with 2000 sides rather than a circle but I don’t think that accounts for it. I can’t see where an error could creep in. It needs someone else to do it independently.
I will upload a couple of versions of the applet for you to see.
By the way, it’s interesting that you’re getting a shape with bilateral symmetry. It seems very plausible… but intriguingly, the best known upper bound—that is, the convex universal covering with least area known so far, due to Hansen—lacks bilateral symmetry. So, the symmetry of the best convex universal covering is still an open question.
I am now finding that when there are more shapes the optimal solution does not have bilateral symmetry. It seems to be a feature of simple cases only. In theory the symmetry could return with the full set of shapes but I have no reason to think that.
Cool! Being left-handed, the spontaneous breaking of chiral symmetry has always fascinated me.
If Philip’s asking a slightly different question (about a 2000-gon rather than a circle), I’m not surprised he’s getting a different answer for the 5th decimal place for the area. But even the larger difference in the optimal rotation could make sense, if there are two very close local minima near 60 degrees and 61.045 degrees whose values are perturbed by more than their difference when you change from a circle to a 2000-gon.
I find I can get a more stable result by fixing the angle and plotting the answer as a function of this angle. There seem to be minima at 12 degree intervals where the solution has bilateral symmetry, but there are two cases, so one absolute minimum area and another local minimum area.
I think it’s also worth stressing that Brass and Sharifi’s 0.833646-area configuration is just the lowest area configuration they happened to encounter in a specific strategy for proving a lower bound of 0.832 on all circle/triangle/pentagon configurations. I don’t think they’re making any strong claims about the detailed geometry of the configuration that actually achieves the lowest area.
Great work Philip, and very interesting so far! It’s ez to backseat drive, but what do you think about the difficulty of tweaking your app to use a real circle? (And as long as I’m backseat driving I’ll second your call for independent confirmation:-)
I dont have the resolve to do the whole thing for exact circles, but I can take the final positions and recalculate once with a very large number of sides to be sure I have the right area. Brass and Sharifi just claim that their area is the minimum known for these three shapes but they seem to have missed the simplification of looking at the case with bilateral symmetry. This seems to give a smaller area solution. I will check it all carefully and write it up.
A single-pass tweaking strategy seems to be: a) compute hull of non-circle polygons, b) replace certain individual hull segments (or segment runs) with: tangent segment + circle arc + tangent segment. I don’t yet see how to handle all cases properly in a clean way though.
I don’t have time to work on this today but in the meantime here is a version that runs with a circle and regular Reuleaux figures of 3,5,7,9 and 11 sides. http://vixra.org/Lebesque/ Reload it it to get a different run. You may need latest Java plugin. This is just a demo, still a lot to do to get real answers.
Thanks for sharing the demo, fascinating Philip!
Apologies if the discussion has answered this already, but what is the relationship between area-minimization and perimeter-minimization for convex hulls such as this?
In any case the impression of the hull as an elastic band is nearly irresistible.
Minimum perimeter would presumably give a different answer. It’s another thing I could easily try.
I have updated the demo at http://vixra.org/Lebesque/ to a version that includes some random shapes of diameter one. You can run it a few times to see what is the smallest area for this set of shapes. I get something around 0,8373. This is an upper bound on a lower bound so it does not prove anything but the interesting thing is the shape of the best solutions.
I fixed the position of the Reuleaux triangle and have drawn a hexagon around it in the background. The best solutions take the approximate form of this hexagon with some straight edge bits cut off, which suggests a strategy for improving the upper bound.
This demo is a cut down version that runs quickly. I am doing bigger runs with more shapes and a much slower cooling rate. I will post some pictures of the best results I get later.
Philip wrote:
This is great! It looks like you include some shapes lacking bilateral symmetry. That’s great. I hope for every such shape you also include its mirror-image version: otherwise the idea that we get a spontaneous breaking of bilateral symmetry is not being tested.
I generate random shapes by throwing diameters on the floor and checking to see if all the end points fall inside a shape with the same diameter. I do also include mirror images for the reason you give.
What I am finding is that after a long run I get a minimum shape that is a hexagon with three of the corners trimmed. The area is about 0.839 and is not symmetrical. However, I do not know if this is a genuine solution to the problem. It may be that my set of shapes just does not include the ones that would stretch into the corners.
Today I am going to change strategy. If you were allowed just one shape then the circle maximises the area. If you allow two shapes than the circle and the reuleaux triangle maximise the area (i.e. they maximise the minimum area of a convex shape that covers them) What third shape maximises the area when combined with those two? I will generate random shapes to look for a solution to this. Then I will look for a fourth shape etc. This way i can build up a minimal set of shapes that stretches the area as much as possible. It should be more efficient.
That’s cool! I hope I can lure you into writing a little article on this subject for Azimuth.
Here are two little ideas I had:
1) You could use your work to construct a shape that you conjecture is a universal covering… perhaps adding a bit of slack if you’re feeling cautious. People could then try to refute this conjecture by finding diameter-1 sets that don’t fit. This would ‘crowd-source’ the project of finding a small universal covering.
2. Perhaps as you lower the temperature in your simulated annealing process there is a phase transition, with bilateral symmetry spontaneously broken below this temperature. Technically speaking, phase transitions only arise for systems with infinitely many degrees of freedom, but for a large but finite collection of diameter-1 shapes there might be an ‘approximate’ phase transition, where the free energy, and the expected values of some interesting quantities, change very rapidly at some temperature.
By the way: the guy’s name is ‘Lebesgue’, not ‘Lebesque’ as you have in this URL:
http://vixra.org/Lebesque/
Those are good ideas. The easiest is to set up small sets of about 4 to 5 shapes. With that few it is possible to get the minimum area with reasonable confidence to set an empirical lower bound.
The second thing would be to set up a shape such as the hexagon with bits lopped off and try to see if anyone can find shapes that dont fit. I could set up a version of the applet for that. It might set an empirical upper bound.
Thirdly I can set up a run with a good selection of shapes like the current demo but better. It might provide clues about what the shape looks like.
Finding the phase transitions would be harder. The runs I am doing so not use a true thermal simulation. What I do is make small trial changes and compute the area of the hull. The the area goes down I accept the change. If it goes up I accept the change with probability 0.3. So it is more like a biased random walk. I just vary the size of the trial changes to cool it down.
Yesterday I was looking at better ways of generating shapes that push the boundaries more. I can construct a two parameter set of irregular shapes of constant diameter with 5 arcs. I am also going to add in the shapes with six arcs shown at http://en.wikipedia.org/wiki/Curve_of_constant_width
And I must fix the spelling error :-)
Philip, I’m curious why you decided to go with a fixed 0.3 probability of accepting increases to the area, rather than with the inverse exponential function used in std SA. Did you find that it worked better for this application?
That’s an interesting question. What you are describing is the metropolis algorithm (described rather tersely at http://en.wikipedia.org/wiki/Metropolis%E2%80%93Hastings_algorithm) This uses a temperature parameter that you slowly decrease. You have to do it this way if you are doing a statistical simulation where the dependence on temperature is what you are interested in, but
The problem is that you have to match the size of the trial changes to the temperature in a complex way. If you make the changes too big or too small the algorithm does not work. These sizes have to be varied as the temperature drops and it is complicated to get it to work. Instead you can just use a biased random walk as I have. Then you sont have to worry about matching the temperature to the size of the changes.
Thanks Philip for the Metropolis-Hastings pointer. You might want to also look at the wikipedia article on Simulated Annealing. When I did something with SA long ago, I don’t recall having to tune the trial changes to match the temperature in any complex way. There was some tuning, but it was pretty simple (maybe a single parameter to control the temperature schedule, and another constant in the exponent of the probability acceptance function).
(Below, you mention the need to check by hand to avoid getting stuck in local minima; so I’m poking at this once more because the SA metaheuristic – with its decreasing temp and monotonically decreasing probability acceptance function – can sometimes be very effective at that:-)
Okay, I may have been overreacting to suggest that Philip being right would imply Brass and Sharifi are wrong. Given their rather exhaustive search through over 53 million configurations, it seemed odd that they’d settle on one where the pentagon is 1° off from the best possible value. I have trouble believing there are two close local minima near 60 degrees and 61.045 degrees…. that just doesn’t feel right. But if being off 1 degree really only changes the area in the fifth decimal place, Brass and Sharifi’s argument would tolerate that kind of error, since they’re just aiming for 3 decimals of accuracy.
Yeah, my remark about “two close local minima” was silly. Sorry. More to the point is what the authors themselves say:
They generated all these specific configurations on discrete grids in the 4-dimensional translation space, using a different grid for each fixed rotation angle for the pentagon, and each time using the coarsest grid they could get away with and still prove their chosen lower bound by making use of the area and some other data at these grid points.
In that context, I don’t think it’s surprising that Philip can find a slightly smaller area for a specific configuration than the smallest area Brass and Sharifi happened across, given that they were trying to deal with as few specific configurations as possible.
In the blog post:
I think this statement is potentially a bit confusing.
The shape in question was merely the one with the least area that was seen by Brass and Sharifi during the implementation of their algorithm, but they weren’t actively searching for the least-area convex shape containing a triangle/circle/pentagon, and they certainly don’t claim that this is such a least-area configuration.
Okay, I tried to fix this.
I’ve set up two new demos at http://vixra.org/Lebesgue1 and http://vixra.org/Lebesgue2. I want to know the minimum area these two demos can give so please post your lowest answers.
Everyone should check out Philip Gibb’s applets:
• http://vixra.org/Lebesgue1/ : circle, Reuleaux triangle, Reuleaux pentagon, Reuleaux septagon
• http://vixra.org/Lebesgue2/ : circle, Reuleaux triangle, Reuleaux pentagon, Reuleaux septagon, Reuleaux nonagon
All these Reuleaux polygons are regular: all the sides and angles look the same. I think to make the fastest progress beyond these it will be good to a look at a non-regular Reuleaux triangle.
Do you mean a non-regular reuleaux pentagon? The triangle has to be regular I think. If so I agree. The regular shapes seem to be most important along with some irregular versions that are close to regular. Other shapes I tried so far just turn out to fit inside what we already have and make no difference, but I could be missing some possibilities.
I meant ‘triangle’, but maybe I was confused. Does every non-regular Reuleaux triangle of diameter 1 fit inside some other famous shapes of diameter 1? If so, I was confused and we should go up to a quadrilateral or pentagon. I see you’re including two irregular pentagons here:
http://vixra.org/Lebesgue3/
Are you counting shapes like the one at http://en.wikipedia.org/wiki/Curve_of_constant_width as reuleaux triangles? You might be right, those could be useful too.
Yes, this is what I’m calling a Reuleaux triangle:
(click for details). This curve reduces to the classic ‘equilateral’ Reuleaux triangle when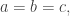
, but it’s always a curve of constant width, and when this width is 1, I was thinking it could be a good to include some curves of this sort in your simulated annealing applet.
You need a=b=c=1 to get the reuleaux triangle. I tried some examples with a=b=c but could not find any that do not fit inside the triangle+circle. I will try harder. By the way Wikipeidia does not call this more general shape a reuleaux triangle but they do not give a reference to where it came from. Did Reuleaux know about it? It would be useful to have some different terminology.
Today I will concentrate on working out which shapes do not fit inside the triangle+ circle
I thought it’d be interesting to see what a couple of families of curves of constant width 1 constructed from triangles looked like, following the recipe given in the Wikipedia article:
• Curves of constant width, Wikipedia.
for the case of zero “padding”.
These are isosceles triangles (up to an equilateral triangle, which gives the Reuleaux triangle):
These are right triangles, with the smallest angle up to 45 degrees:
The changing scales of the triangles are forced by the requirement that the constant width that follows from the construction is 1 in all cases.
The dashed curve on these images is a circle of diameter 1, for comparison. The zero-angle limit of either family of triangles is that circle.
Interestingly (at least to my eye, I haven’t proved this) it seems that within either of these 1-parameter families, none of the curves will fit inside any of the others.
Greg, that looks good. What I cant see is whether all those shapes fit inside the convex shape formed by a circle and triangle with the same centre, i.e the shape that gives a lower bound of 0.825.
Shapes that do not fit inside are useful. I am currently plotting which pentagons do not fit inside.
The envelope of the 1-parameter family of curves of constant width 1 generated from isosceles triangles (when they’re arranged as they are in the image from my previous comment) has an area of:
That’s only about 0.005 above Pál’s smallest area for a universal cover, which is intriguing. I think I’ll have to stare at this for a bit longer before it becomes clear that the arrangement that yields this envelope isn’t the minimal area configuration for these shapes … but of course it can’t be, because that would contradict Pál.
Perhaps the envelope would be smaller if you centre them on their centre of area.
Philip, I can answer your question for the isosceles case:
That also answers my own question: what configuration of these shapes reduces the area of their envelope compared to the “natural” placement in the previous image? This image has each curve displaced along the x-axis by:
where
is the small angle of the isosceles triangle on which the curve is based.
For what it’s worth, I’m about 90% sure that all the curves of constant width 1 derived from right-angled triangles also fit inside the convex hull of a concentric circle and an equilateral triangle of diameter 1.
I can’t find a nice general formula for the rotation+translation, but case by case they all seem to fit … and if any of them don’t, it will certainly be a very small area that lies outside.
That is interesting. In that case it is likely that all this type of shape fit inside the triangle + circle. Even if this is true there is a small chance that such shapes are important because the overall solution may not have the centre for the triangle coinciding with the centre of the circle.
I’ve been wondering if a fruitful technique to obtain new lower bounds might be the following:
(1) Find a 1-parameter family of curves of constant width 1, labelled by a parameter
, such that the interior of 
can’t be rotated and translated to fit inside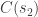 
for 
, and each separate shape puts a slightly different demand on the cover. The families of curves obtained from triangles seems to have that property.
(2) Imagine translating and rotating each member of the family by some as-yet-unspecified functions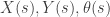
to yield a new family of curves, 
.
(3) Compute the envelope of the family of curves
, and its area ![A[X(s), Y(s), \theta(s)]](https://s0.wp.com/latex.php?latex=A%5BX%28s%29%2C+Y%28s%29%2C+%5Ctheta%28s%29%5D&bg=ffffff&fg=333333&s=0&c=20201002)
, a functional of 
.
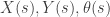(4) Use the calculus of variations to minimise![A[X(s), Y(s), \theta(s)]](https://s0.wp.com/latex.php?latex=A%5BX%28s%29%2C+Y%28s%29%2C+%5Ctheta%28s%29%5D&bg=ffffff&fg=333333&s=0&c=20201002)
.
My completely unproven hunch is that applying this process to the family of curves derived from isosceles triangles would yield the convex hull of a circle and a concentric equilateral triangle, which would be nice! Obviously that’s no advance on Brass and Sharifi, but a sufficiently clever choice of a different 1-parameter family might yield a higher lower bound.
Greg, your calculus of variations proposal is interesting. Do you really think that you can calculate the envelope of the infinite family of curves though? That seems hard.
Greg,
On reading further I see that you *can* apparently calculate the area of an infinite family of such curves, for at least a couple of specific choices of translation and rotation function. And I gather that you think the general case would be similarly doable. Pardon me for being a doubter!-)
For 1-parameter families of constant-width curves that are just collections of circular arcs (whose centres and radii are functions of the parameter that labels the family), it’s not hard to write down parametric formulas for the pieces of the envelope that are due to each arc, in terms of the centre and radius functions and the functions describing the overall rotation and translation of each curve.
One tricky aspect, though, is keeping track of the exact points where each of these envelope curves joins or leaves the border of the region whose area we want to know. I haven’t yet got as far as working through the whole exercise for the simplest case, the CCW based on isosceles triangles.
Greg, thanks for the clarification about calculating the envelope of these families of constant-width curves. If it turns out that the ‘tricky aspect’ you mention can’t be resolved, would it be of any value to instead just use families of polygons? This would I think avoid the tricky aspect; that said, I am not sure that your proposed approach would still be a) meaningful, b) useful if modified in this way.
I withdraw my message of 18 December, 2013 at 2:47 am mentioning a possible tweak to Greg’s calculus of variations based proposal. Having read Greg’s proposal more carefully, I don’t think my suggested tweak to it makes much sense.
In a previous comment of mine that’s so indented that direct replies to it are impossible:
… I described the placement of curves of constant width based on isosceles triangles in such a way that (I thought) they would fit perfectly inside the circle-plus-concentric-equilateral-triangle.
It turns out that the formula I gave there almost works (and by eye, in the image included in that comment, it looks very convincing) — but in fact, that formula does not make the envelope of the family of CCWs coincide with the boundary of the triangle.
The correct displacement along the x-axis for those isosceles-based CCWs is:
where
is the altitude of the isosceles triangle. This makes the envelope coincide exactly with the boundary.
Ah, I just managed to reproduce this formula for positioning the 1-parameter family of isosceles-based CCWs:
from a stationary point in the area functional! (I’d previously derived it by assuming the answer I wanted for the envelope.)
For the area functional calculation I did assume no rotation and no y-translation (which seemed reasonable when the whole family of shapes has bilateral symmetry) so the single unknown function was the x-translation of each CCW. But given those assumptions, requiring a stationary point in the area implies the quadratic function shown above, and the envelope with minimal area is the circle-plus-concentric equilateral triangle.
So you are making progress on your proposal – great work! Assuming you confirm that this x-translation function, together with y-translation and rotation functions which are identically zero, is indeed area-minimizing for the family of curves you’re dealing with, where does that leave us?
Philip, if I roughly understand this you are looking at many sets of test shapes in attempt find a set of shapes whose near-minimum convex hull area (over a large number of translations and rotations of the shapes in the set) is as large as possible.
If so, you might have more time for holiday cheer if you consider using SA at *both* levels of the search – i.e. not just to minimize the convex hull area for a given set of shapes, but also to search for a near-maximal shape set.
This might seem odd if one assumes that the search space for SA is continuous. But I think I remember from long ago examples of SA working well in a discrete search space, as long as the objective function is continuous – e.g. a VLSI CAD application in which SA was used to optimize the placement within a 2D lattice of a large number of rectangular ‘cells’, with the objective of minimizing total interconnect length. The basic perturbation move was to swap the locations of two randomly selected cells.
Just a thought. In any case, thanks for charging ahead as you have – great work!
Yes effectively it is a double optimisation problem where you look for the maximum of the minimum. A double SA is effectively what you have to do, but the problem is that the system can get stuck in local minima. You have to keep checking by hand to be confident that you are looking at the right minimum.
After a lot of annealing I am starting to get more of a feel for how this problem works. The solutions we get always fit neatly into a hexagon which fits around the circle and the Reuleaux triangle when their centres are close but not necessarily coincident. These hexagons have opposite sides parallel and distance one apart. It seems like a good strategy to assume this is the case as a hypothesis and explore the two parameter space of such hexagons.
Given such a hexagon I think any curve of constant width will fit inside in a discrete number of ways (maybe 6 ways, I need to check this) so it requires an efficient search strategy over the 6^n possibilities given some set of n shapes plus the triangle and circle.
Another observation is that the shapes that matter most are the regular Reuleaux polygons with an odd number of sides. Apart from these the only shapes that could matter are some irregular Reuleaux polygons that are quite close to the regular ones.
Unless I’m confused, there’s a 3-parameter space of hexagons with three pairs of parallel sides each separated by distance 1: two angles and an overall scale for the triangle into which the hexagon can be inscribed. Is there some further restriction on the solutions?
Yes I am only interested in the hexagons formed around a circle and Reuleaux triangle so the only parameters are the offset for their centres and those are also bounded by the requirement that the circle must intersect the triangle in six places. So it is not every hexagon with parallel sides a unit distance apart. The way I described it did not make that very clear.
Is this a correct recipe for constructing the hexagons?
(1) Take a circle of diameter 1 and a Reuleaux triangle of width 1, with some choice of an offset between their centres such that the circle intersects the triangle at six points.
(2) The three vertices of the Reuleaux triangle are three vertices of the final hexagon. From each of these three vertices, and in each direction (i.e. clockwise and counterclockwise) construct an edge of the hexagon by choosing a line segment that is either (a) tangent to the arc of the Reuleaux triangle at the vertex, or (b) will be tangent to the circle at some point, making the choice so that the edge avoids crossing into the interior of either shape.
(3) The remaining three vertices are determined by the intersections of the edges we’ve just constructed.
If this is the correct recipe, it won’t always yield three pairs of parallel sides for the hexagon.
I think that by symmetry you can further restrict the configs to those in which the circle’s center lies within a certain 60 degree ‘pie slice’ of the Reuleaux triangle (delimited by a perpendicular bisector and an angle bisector intersecting the same side of the triangle).
I’m pretty sure that the “some choice of an offset between their centres” places the circle’s center within a deltoid-like region defined by 3 arcs of radius 0.5 centered on each vertex of the Reuleaux triangle. And the symmetry consideration cuts this down by a factor of 6 to a wedge of area 1/6(sqrt(3)/4 – pi/8).
Hi John,
all regular 2n-gons with diameter 1 fit into the unit circle… That’s easy to see because their 1-diameters all run through the centre, so each 2n-gon is just the circle with 2n pieces chopped off.
I wonder if we could also start finding “best envelopes” for all 3n-gons, all 5n-gons, 7n-gons etc. and then try to find a minimal cover of those envelopes. Then the prime numbers would play a prominent role here.
Of course, search processes like simulated annealing (as mentioned before) or genetic algorithms would be well suited to find good solutions.
Best regards
Till
Till wrote:
Right.
Good idea. As I mentioned, Elekes got a lower bound of
0.8271
by considering the circle and regular 3n-gons of diameter 1 for all n:
• Gy. Elekes, Generalized breadths, circular Cantor sets, and the least area UCC, Discrete & Computational Geometry 12 (1994), 439–449.
He did this analytically. However, Brass and Sharifi note that using just a circle and triangle gives a convex hull with area
0.825
So, the 9-gon and higher 3n-gons don’t contribute much: a measly 0.0021!
We could try to use all 3n-gons, but as you note, the hexagon and 12-gon don’t contribute at all… so we’d only beat Elekes when we reached the 15-gon, which probably won’t help much.
Similarly, using the circle together with all 3n-gons and all 5n-gons will probably be not much better than what Brass and Sharifi did with the circle, triangle and pentagon:
0.832
Nonetheless it would be interesting to try your strategy and compare it to others. It’s possible that a less symmetrical shape would help more!
Sort of running further (but also into left-field) with this ideas. What happens if we place the restriction that instead of all diameter-1 sets, we consider all diameter-1 sets whose boundary is constructable using straight-edge and compass? Or in the other direction, we allow all sets, but ask our cover’s boundary to be constructable with straight-edge and compass. This doesn’t seem to change much of the approaches that have been discussed so far, while giving us many more handles on these sets.
Artem wrote:
Since any diameter-1 set can be approximated arbitrarily well by such ‘constructible’ sets, the answer to Lebesgue’s universal covering problem won’t change if we do this.
(Technically, what I mean is that for any compact subset
of the plane with diameter 
and any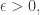 
there’s a compact subset 
with constructible boundary, also with diameter 
whose Hausdorff distance from 
is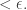 
)
If the universal covering with minimal area has a boundary that’s not constructible, we won’t find it if we impose this constraint—but we can find a universal covering with constructible boundary whose area comes as close as we like to the minimum.
(This is for similar reasons to the above remark. Compact sets with constructible boundary are dense among all compact subsets of the plane if we use the Hausdorff distance.)
Here is a free online source of Elekes article:
http://gdz.sub.uni-goettingen.de/dms/load/img/?PPN=GDZPPN000366943&IDDOC=219746
My intention with the minimum covers of {p_i*n-gons, n=1..infinity}, p_i = i.th prime, was to decompose the problem into simpler problems. Like the {3^j-gon}-solution of Elekes, it might be that the minimum cover of {p_i*n-gons} for fixed p_i are concentric and equally aligned, thus much simpler then assembling arbitrary x- and y-gons. But the shape of these covers may also be of academic interest on their own.
I am not sure if the minimum cover of the (minimum cover of the {p_i*n-gons}) gives the answer to Lebesque’s question, though – the division into two steps may be too restrictive. But it’s not impossible.
If we leave out the p_i*n-gons that do not contribute because they have already been added by a p_j<p_i (like the hexagon and 12-gon you mentioned), then we get the sieve of Erasthotenes:
p_i=2: 2, 4, 6, 8, 10, 12, 14, 16, 18…
p_i=3: 3, 9, 15, 21, 27, 33, 39, 45, …
p_i=5: 5, 25, 35, 55, 65, 85, …
p_i=7: 7, 49, 77, 91, 119, …
p_i=11: 11, 121, 143, 187, …
…
(cmp. http://oeis.org/A083140)
Probably this does not lead anywhere – but it helped me understand that the minimum cover of the set of regular p_i*n-gons, n=1..inf, p_i fixed, arranged around a common centre, converges to the unit circle “plus some small elevations at the corners” of the regular polygons.
Indeed these additions at the corners are much bigger the smaller the n of an n-gon is. So I understand now that additionally to a unit circle, the n-gons with smallest n are definitely most important.
I calculated how far a corner of a regular n-gon elevates above a unit circle centrically aligned with the n-gon. This is just trigonometry. Compared with the radius of the unit circle being 1/2, the distance d of the centre to a corner of an n-gon is 0.5 / cos(PI / (2n)).
For example we get for
n=3 (triangle): d~0.57735027
n=5: d~0.52573111
n=7: d~0.51285843
n=9: d~0.50771331
n=11: d~0.50514161
We could probably compute the area of the “corner-pieces” standing out of the unit circle, too. But the difference of the normals to the unit circle radius 1/2 already shows that the influence of n-gons with bigger n is decreasing quickly.
Something I did not understand yet: Is
also a lower bound for the non-convex universal cover?
To expand on Andy’s reply: any universal covering has to contain the disk of diameter 1, so it has to have area at least
We can easily improve this by taking the union of a disk of diameter 1 and a triangle of diameter 1 sharing the same center. The area of this set is a lower bound on the area of any universal covering, convex or not. I haven’t calculated this number, though it’s easy to do.
If we consider only convex universal coverings we can boost the lower bound further, to the area of this:
which is about 0.825.
Oh wow! Thanks for all that! Once upon a time I was a measure theory freak. And now an epic Lebesgue story with no mention of the axiom of choice and only one occurence of the word “measure”!
Glad you liked it. I’m still a bit of a measure theory freak, and this quarter I was teaching the first quarter of U. C. Riverside’s real analysis course, which is mainly measure theory… so these things are on my mind. This Lebesgue universal covering problem reminds me slightly of the Lebesgue number lemma. At least I can see why the same guy would be interested in both.
Definitely.
Greg, your calculus of variations proposal is interesting. Do you really think that you can calculate the envelope of the infinite family of curves though? That seems hard.
Is that a new question? What is the diameter of the solution of the Lebesgue universal covering problem?
EB wrote:
Is what a new question? I wrote:
So, that is not a new question.
Nobody knows the solution of the problem, and I don’t think anyone knows the diameter of the solution of the problem, either.
What is the diameter of the best solutions sofar?
I don’t know. Since the puzzle is about trying to minimize the area, I just know the area of the best solutions so far: read the blog article for that. You can also take the information I present, including the articles linked to, and use those to compute the diameters of the proposed solutions.
Yes. Thanks. The diameter is clearly bigger than 1. You don’t be enthusiastic for this NEW question. ;-)
I like the question because there is some “recursive” character. You can even change the puzzle and ask after a minimal diameter solution instead of the minimal area solution!
It would be a straightforward exercise to work out the diameter of Sprague’s solution as described in the article and I dont think the later refinements made the diameter smaller. A more difficult question would be “what is the minimum diameter for any (convex) universal covering?” rather than “what is the minimum area?” as Lebesgue asked (or minimum perimeter as arch1 asked earlier) These questions might have completely different answers.
In the study of Brass&Sharifi 2005 the constellation circle-triangle-pentagon is almost symmetric about a line from the lower left angle of the triangle to the pentagon vertex at the upper right. The eccentricities are okay, but I think that this symmetry should not be destroyed. Now you have only 2 instead of 5 parameters to optimize. Adding the heptagon to the considerations would increase this number only to 3 (instead of 7) and this is perfectly manageable.
To get the symmetry you change the Brass&Sharifi parameters from .00617284, .0037037 (triangle) and .0197531, .0148148, 61.045 (pentagon) to .00623426, .0035993 (triangle) and .0213833, .0123456, 60 (pentagon). I think that the convex hull area is not bigger.
I think this is the same symmetry I pointed out before https://johncarlosbaez.wordpress.com/2013/12/08/lebesgues-universal-covering-problem/#comment-34473 If you add enough shapes you eventually lose this symmetry but you can always study a variant of the problem where everything is required to be symmetrical.
It turns out that the really useful observation about solutions for a fixed set of shapes is that they seem to fit inside a hexagon with opposite sides parallel and distance one apart. This ultimately reduces the problem to a two parameter family of hexagons with only a finite number of ways of placing the shapes in each hexagon, if it can be proven.
I have written the bilateralized Brass&Sharifi form in a PostScript file as follows
%!PS-Adobe-2.0 EPSF-2.0
%%Title: LebesgueUniversalCovering, Brass&Sharifi, symmetric, Ed Baumann, 2014
%%BoundingBox: -60 -60 60 60
%%EndComments
100 100 scale
0 setlinewidth
% tangent 1
0.476679844 0.275211236 moveto
0.497875043 0.046048256 lineto
0 0 lineto
closepath
stroke
% tangent 1 sym
0.476679844 0.275211236 moveto
0.288816481 0.408148307 lineto
0 0 lineto
closepath
stroke
% tangent 2
0.506234261 -0.285075782 moveto
0.499884855 0.010729936 lineto
0 0 lineto
closepath
stroke
% tangent 2 sym
0.006234261 0.580949621 moveto
0.259234825 0.427548016 lineto
0 0 lineto
closepath
stroke
% tangent 3
0.506234261 -0.285075782 moveto
0.250000066 -0.433012664 lineto
0 0 lineto
closepath
stroke
% tangent 3 sym
0.006234261 0.580949621 moveto
-0.249999934 0.43301274 lineto
0 0 lineto
closepath
stroke
% stright between triangle-vertex and pentagon-vertex
-0.493765739 -0.285075782 moveto
-0.192450763 -0.467933589 lineto
0 0 lineto
closepath
stroke
% stright between triangle-vertex and pentagon-vertex, sym
-0.493765739 -0.285075782 moveto
-0.501467757 0.067299545 lineto
0 0 lineto
closepath
stroke
% tangent 4
-0.192450763 -0.467933589 moveto
-0.117152712 -0.486081518 lineto
0 0 lineto
closepath
stroke
% tangent 4 sym
-0.501467757 0.067299545 moveto
-0.479535299 0.141583534 lineto
0 0 lineto
closepath
stroke
% Zentrum Triangle
0.003734261 0.007929479
moveto
0.008734261 -0.000730775
lineto
stroke
% Zentrum Pentagon
0.018883345 0.016675807
moveto
0.023883345 0.008015553
lineto
stroke
% Arcs
0 0 0.5 1.229654477 5.284229375 arc stroke
0 0 0.5 -103.5506835 -59.99999123 arc stroke
0 0 0.5 54.71577062 58.77034552 arc stroke
0 0 0.5 119.9999912 163.5506835 arc stroke
This allows a good zooming in the picture. See pictures in http://edu1618.jimdo.com/2014/02/07/durchmesser-eins/
@Gibbs: can you do the same for your marvelous 0.844112 forme? Please.
John Baez: Can you reach Brass&Sharifi to communicate this new idea?
What about “Add the nonagon (4 parameters in all), add the 11-gon (5 parameters) and so on?”
Sorry, I don’t know Brass and Sharifi any better than you do.
I suggest that you contact Phil Gibbs, who commented on this post above. He’s written a new paper on this problem:
• Philip Gibbs, A new slant on Lebesgue’s universal covering problem.
I will blog about this soon. But I know you’d enjoy reading it!
The diameter of the bilaterized circle-triangle-pentagon-shape used by Brass&Sharifi is 1.12057 (1). For this shape I have calculated the postsript description which is a finite liste of strokes and arc strokes. I still ask Ph.Gibbs to establish such a description for his 0.844112 shape (2014). Let LUC(a) be the convex Lebesgue Universal Covering for convex shapes with diameter 1 (allowing translations, rotations and reflections) with minimal area. Then a possible alternative is LUC(d). Same as LUC(a) but with minimal diameter. I don’t know how much (1) must be diminished to be a lower diameter-bond of LUC(d). This demands a big effort as Brass&Sharifi have done for their the lower area-bond for LUC(a) which is 0.832. Trivially diameter 1 is a lower diameter-bond of LUC(d). Who nows a better upper diameter-bond for LUC(d) than the diameter of the circumscribed regular Hexagon to the diameter 1 circle (which is 1.1547 = 2/root(3))?
The minimum diameter variant is mentioned in the book “Research Problems in Discrete Geometry” but only to say that no work has been done on it. Sounds like an opportunity.
Making a vector diagram of the cover would take some work. What are the benefits to make it worth while? :-)
A while back I described a century-old geometry problem posed by the famous French mathematician Lebesgue, inventor of our modern theory of areas and volumes. This problem is famous for being difficult and frustrating. So, I’m happy to report some new progress:
• John Baez, Karine Bagdasaryan and Philip Gibbs, Lebesgue’s universal covering problem.
But we’d like you to check our work! It will help if you’re good at programming.
Our paper on this subject has now been published:
• John Baez, Karine Bagdasaryan and Philip Gibbs, The Lebesgue universal covering problem, Journal of Computational Geometry 16 (2015), 288-299.
The referees caught a number of mistakes, so if you ever got ahold of an earlier version of this paper, and if you care, please get the new one. The journal is open-access, so it’s free.
[…] μαθηματικός John Baez,από το Πανεπιστήμιο της Καλιφόρνια, όταν έγραψε γι αυτό στο ιστολόγιό του. «Το ενδιαφέρον μου για αυτό το πρόβλημα είναι μάλλον […]
Baez lifted Lebesgue’s universal covering problem out of obscurity when he wrote about it in 2013 on his popular math blog. He confessed he was attracted to the problem the way you might be attracted to watching an insect drown.
Baez lifted Lebesgue’s universal covering problem out of obscurity when he wrote about it in 2013 on his popular math blog. He confessed he was attracted to the problem the way you might be attracted to watching an insect drown.
“My whole interest in this problem is rather morbid,” Baez wrote. “I don’t know any reason that it’s important. I don’t see it as connected to lots of other beautiful math. It just seems astoundingly hard compared to what you might initially think. I admire people who work on it in the same way I admire people who decide to ski across the Antarctic.”