guest post by Vanessa Schweizer
This is my first post to Azimuth. It’s a companion to the one by Alaistair Jamieson-Lane. I’m an assistant professor at the University of Waterloo in Canada with the Centre for Knowledge Integration, or CKI. Through our teaching and research, the CKI focuses on integrating what appears, at first blush, to be drastically different fields in order to make the world a better place. The very topics I would like to cover today, which are mathematics and policy design, are an example of our flavour of knowledge integration. However, before getting into that, perhaps some background on how I got here would be helpful.
The conundrum of complex systems
For about eight years, I have focused on various problems related to long-term forecasting of social and technological change (long-term meaning in excess of 10 years). I became interested in these problems because they are particularly relevant to how we understand and respond to global environmental changes such as climate change.
In case you don’t know much about global warming or what the fuss is about, part of what makes the problem particularly difficult is that the feedback from the physical climate system to human political and economic systems is exceedingly slow. It is so slow, that under traditional economic and political analyses, an optimal policy strategy may appear to be to wait before making any major decisions – that is, wait for scientific knowledge and technologies to improve, or at least wait until the next election [1]. Let somebody else make the tough (and potentially politically unpopular) decisions!
The problem with waiting is that the greenhouse gases that scientists are most concerned about stay in the atmosphere for decades or centuries. They are also churned out by the gigatonne each year. Thus the warming trends that we have experienced for the past 30 years, for instance, are the cumulative result of emissions that happened not only recently but also long ago—in the case of carbon dioxide, as far back as the turn of the 20th century. The world in the 1910s was quainter than it is now, and as more economies around the globe industrialize and modernize, it is natural to wonder: how will we manage to power it all? Will we still rely so heavily on fossil fuels, which are the primary source of our carbon dioxide emissions?
Such questions are part of what makes climate change a controversial topic. Present-day policy decisions about energy use will influence the climatic conditions of the future, so what kind of future (both near-term and long-term) do we want?
Futures studies and trying to learn from the past
Many approaches can be taken to answer the question of what kind of future we want. An approach familiar to the political world is for a leader to espouse his or her particular hopes and concerns for the future, then work to convince others that those ideas are more relevant than someone else’s. Alternatively, economists do better by developing and investigating different simulations of economic developments over time; however, the predictive power of even these tools drops off precipitously beyond the 10-year time horizon.
The limitations of these approaches should not be too surprising, since any stockbroker will say that when making financial investments, past performance is not necessarily indicative of future results. We can expect the same problem with rhetorical appeals, or economic models, that are based on past performances or empirical (which also implies historical) relationships.
A different take on foresight
A different approach avoids the frustration of proving history to be a fickle tutor for the future. By setting aside the supposition that we must be able to explain why the future might play out a particular way (that is, to know the ‘history’ of a possible future outcome), alternative futures 20, 50, or 100 years hence can be conceptualized as different sets of conditions that may substantially diverge from what we see today and have seen before. This perspective is employed in cross-impact balance analysis, an algorithm that searches for conditions that can be demonstrated to be self-consistent [3].
Findings from cross-impact balance analyses have been informative for scientific assessments produced by the Intergovernmental Panel on Climate Change Research, or IPCC. To present a coherent picture of the climate change problem, the IPCC has coordinated scenario studies across economic and policy analysts as well as climate scientists since the 1990s. Prior to the development of the cross-impact balance method, these researchers had to do their best to identify appropriate ranges for rates of population growth, economic growth, energy efficiency improvements, etc. through their best judgment.
A retrospective using cross-impact balances on the first Special Report on Emissions Scenarios found that the researchers did a good job in many respects. However, they underrepresented the large number of alternative futures that would result in high greenhouse gas emissions in the absence of climate policy [4].
As part of the latest update to these coordinated scenarios, climate change researchers decided it would be useful to organize alternative futures according socio-economic conditions that pose greater or fewer challenges to mitigation and adaptation. Mitigation refers to policy actions that decrease greenhouse gas emissions, while adaptation refers to reducing harms due to climate change or to taking advantage of benefits. Some climate change researchers argued that it would be sufficient to consider alternative futures where challenges to mitigation and adaptation co-varied, e.g. three families of futures where mitigation and adaptation challenges would be low, medium, or high.
Instead, cross-impact balances revealed that mixed-outcome futures—such as socio-economic conditions simultaneously producing fewer challenges to mitigation but greater challenges to adaptation—could not be completely ignored. This counter-intuitive finding, among others, brought the importance of quality of governance to the fore [5].
Although it is generally recognized that quality of governance—e.g. control of corruption and the rule of law—affects quality of life [6], many in the climate change research community have focused on technological improvements, such as drought-resistant crops, or economic incentives, such as carbon prices, for mitigation and adaptation. The cross-impact balance results underscored that should global patterns of quality of governance across nations take a turn for the worse, poor governance could stymie these efforts. This is because the influence of quality of governance is pervasive; where corruption is permitted at the highest levels of power, it may be permitted at other levels as well—including levels that are responsible for building schools, teaching literacy, maintaining roads, enforcing public order, and so forth.
The cross-impact balance study revealed this in the abstract, as summarized in the example matrices below. Alastair included a matrix like these in his post, where he explained that numerical judgments in such a matrix can be used to calculate the net impact of simultaneous influences on system factors. My purpose in presenting these matrices is a bit different, as the matrix structure can also explain why particular outcomes behave as system attractors.
In this example, a solid light gray square means that the row factor directly influences the column factor some amount, while white space means that there is no direct influence:
Dark gray squares along the diagonal have no meaning, since everything is perfectly correlated to itself. The pink squares highlight the rows for the factors “quality of governance” and “economy.” The importance of these rows is more apparent here; the matrix above is a truncated version of this more detailed one:
(Click to enlarge.)
The pink rows are highlighted because of a striking property of these factors. They are the two most influential factors of the system, as you can see from how many solid squares appear in their rows. The direct influence of quality of governance is second only to the economy. (Careful observers will note that the economy directly influences quality of governance, while quality of governance directly influences the economy). Other scholars have meticulously documented similar findings through observations [7].
As a method for climate policy analysis, cross-impact balances fill an important gap between genius forecasting (i.e., ideas about the far-off future espoused by one person) and scientific judgments that, in the face of deep uncertainty, are overconfident (i.e. neglecting the ‘fat’ or ‘long’ tails of a distribution).
Wanted: intrepid explorers of future possibilities
However, alternative visions of the future are only part of the information that’s needed to create the future that is desired. Descriptions of courses of action that are likely to get us there are also helpful. In this regard, the post by Jamieson-Lane describes early work on modifying cross-impact balances for studying transition scenarios rather than searching primarily for system attractors.
This is where you, as the mathematician or physicist, come in! I have been working with cross-impact balances as a policy analyst, and I can see the potential of this method to revolutionize policy discussions—not only for climate change but also for policy design in general. However, as pointed out by entrepreneurship professor Karl T. Ulrich, design problems are NP-complete. Those of us with lesser math skills can be easily intimidated by the scope of such search problems. For this reason, many analysts have resigned themselves to ad hoc explorations of the vast space of future possibilities. However, some analysts like me think it is important to develop methods that do better. I hope that some of you Azimuth readers may be up for collaborating with like-minded individuals on the challenge!
References
The graph of carbon emissions is from reference [2]; the pictures of the matrices are adapted from reference [5]:
[1] M. Granger Morgan, Milind Kandlikar, James Risbey and Hadi Dowlatabadi, Why conventional tools for policy analysis are often inadequate for problems of global change, Climatic Change 41 (1999), 271–281.
[2] T.F. Stocker et al., Technical Summary, in Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (2013), T.F. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S.K. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex, and P.M. Midgley (eds.) Cambridge University Press, New York.
[3] Wolfgang Weimer-Jehle, Cross-impact balances: a system-theoretical approach to cross-impact analysis, Technological Forecasting & Social Change 73 (2006), 334–361.
[4] Vanessa J. Schweizer and Elmar Kriegler, Improving environmental change research with systematic techniques for qualitative scenarios, Environmental Research Letters 7 (2012), 044011.
[5] Vanessa J. Schweizer and Brian C. O’Neill, Systematic construction of global socioeconomic pathways using internally consistent element combinations, Climatic Change 122 (2014), 431–445.
[6] Daniel Kaufman, Aart Kray and Massimo Mastruzzi, Worldwide Governance Indicators (2013), The World Bank Group.
[7] Daron Acemoglu and James Robinson, The Origins of Power, Prosperity, and Poverty: Why Nations Fail. Website.




Thanks for this article! It’s great to see how this technique gets used in practice and can deliver new insights.
Here are some stochastically generated thoughts:
1) I think Alastair’s post, or something I read, mentioned an interesting ambiguity in the possible interpretations of the Markov chain used in stochastic cross-impact analysis.
One is to think of the Markov chain as an actual process occurring in time: starting with one scenario, as time passes society has a probability of moving to some other scenario. Another is to think of it more abstractly as the process of any given scenario smearing out to the most self-consistent probability distribution of scenarios.
(The statistical mechanics jargon for this kind of “smearing out” is “relaxation”, which leads to some interesting titles involving phrases like violent relaxation.)
It seems that given how you’re generating the transition probabilities in the Markov chain, the latter more abstract interpretation is better. The questions that evoked these probabilities didn’t ask about processes in time, and any unit of time per step—years, decades?—would thus be “made up” by the researcher rather than elicited by the questions. This sounds bad.
Of course one could ask questions like “if the governance is good, how will this affect the population 10 years hence?” Such questions could be used to generate a Markov process that takes place in actual time. That could be interesting. But I don’t think those are the questions that were actually asked.
2) So, let’s think of the equilibrium state of the Markov chain as the “maximally self-consistent probability distribution on the set of scenarios”. Can we make this a bit more precise? Is there some way of quantifying the self-consistency of a probability distribution on the set of scenarios, such that the equilibrium state maximizes this quantity?
There are some obvious guesses to try…
3) Can we think of a principled way of writing this probability distribution as a linear combination of ‘clouds of likely scenarios’?
That’s what we seem to see here:
This is a simple example, just to illustrate the ideas. The idea is that we’ve got a developing country where the population, income and education can be high, medium or low. For example, the big red dot HLL has high population, low income, and low education. That’s a very self-consistent scenario. Other scenarios like HML and LLL are less self-consistent: if we start there, the situation will tend to move towards HLL.
This example is from:
• Vanessa Schweizer, Alastair Jamieson-Lane, Nix Barnett, Hua Cai, Stephan Lehner, Matteo Smerlak, Melinda Varga, Complexity (trans‐)science: a project on forecasting social change.
But my point is that the red ‘cloud’ and the blue ‘cloud’ and the green ‘cloud’ seem like probability distributions that you can take a linear combination of to get the equilibrium state. How were these three clouds arrived at? I forget if they’re the result of an algorithm, or ‘eyeballing’. Now I’m curious!
(In this picture the green cloud looks like it should be subdivided into two separate clouds, so that’s another thing I’m wondering about.)
I agree that the ‘smeared’ interpretation is more relevant. There are multiple reasons for this, one of them being that even socioeconomic conditions that appear stable can change very rapidly into a different state (Great Recession of 2007/2008 anyone?). Currently, I think it is unrealistic (perhaps even dangerous) to view socioeconomic systems as achieving equilibria (perhaps someday humans somewhere will achieve a utopian equilibria and my opinion will be shown to be wrong, but I digress).
However, what may be informative and interesting for policy discussions is some analytical approach that clearly maps ‘forks in the road’ for policy choices and outcomes, as well as where these forks appear to lead. This would be a novel presentation of opportunity costs as risky (or perhaps even lost) pathways between different basins of attraction. For these reasons, I agree with John’s observations regarding ‘clouds of likely scenarios.’
For the ‘clouds’ in the simple example, there are two pieces of information in the figure that John included. The color of the scenarios is arbitrary, where the population outcome set the color (H population is green, M population is red, L population is blue). You should probably just ignore the color. However, scenarios with self loops indicate where the basins are. Adjacent scenarios trace out pathways between the basins. I will let Alastair comment on the probabilities for the network edges, but an algorithm was used to determine which scenarios self loop and what their transition neighbors are.
Probability distributions could be calculated for each cloud. That might be useful. However, my first reaction is that an overall equilibrium state for the system may be less useful for informing policy discussions.
Hmmmm… thinks thinks thinks.
Personally I’m not too averse to treating the transitions as actual transitions- We don’t NEED to know the time step as such, merely that X might lead to Y. But maybe this is just taking too much from a loose model.
Vanessa’s example WRT the recsession is worth noting… but my suspicion is that this transtion was far more likely than previously assumed.
I thinking we do lose a lot from just taking the straight cloud, as we lose the idea of how disjoint two sections of the cloud might be.
We might find that red blue and green clusters are all equally likely, BUT that the transition between red and green is reasonably likely (one in ten chance), while blue is almost totally disjoint (1.in 10,000 chance of transition). To me this seems like useful information. (Here I use colour names only for reference)
The catch of course being that all the transition weights were created using a somewhat arbitrary rule, and thus should not be taken too seriously (the rule is described in previous post)
Personally, I’m most interested in seeing the above technique applied to an actual scenario (perhaps with a fast feedback time), to see how it compares to group and individual opinions, or just random guessing.
Thanks for the comments. I’m a bit amused that Alastair, as a mathematician, is worried about whether these models are exactly right yet more willing than Vanessa to think of the transitions in these Markov processes as transitions that occur in time. Somehow that reminds me of how mathematicians (like myself) can be: we’re ultra-cautious one moment, then when we decide the situation is a bit loose, not bound by ultra-precise rules, we go wild! I’m afraid I side with Vanessa here.
I’m afraid I side with Vanessa here.
More importantly it sounds as if you don’t have an algorithm for taking the equilibrium probability distribution of a Markov process and chopping it into ‘clouds of likely scenarios’. That’s not a criticism, I’m just looking for some way to make myself useful! This could be fun, because it reminds me of ‘resonances’ in particle physics, chemistry etc. A resonance is not a stationary state, it’s an ‘approximately stationary state’ that decays exponentially. If we have a Markov process where the underlying graph has two big pieces connected by just one very low-probability edge, we’ll get two ‘approximate equilibria’ supported on those two pieces. Understanding these quantitatively might be interesting and even useful.
In response to G, John wrote about viewing climate change as the problem of massing force in a struggle for power: “Alas, I don’t know how to personally be effective in ‘going on the attack at the critical targets’.”
Abstracting in terms of game theory, teachers of network theory could be modeled as the force of good in a struggle for power over climate change. While teachers of seat-of-the-pants reasoning about climate change could be the opposing force in this imagined game.
This is, pretty much, how I’ve heard it described about Japanese business strategy as planned by MITI, years ago from a marketing statistics person in the car industry. The example was penetration of sales showrooms into the American market by a certain car company from Japan. He and his mathematical colleagues saw, mathematically, that this was actually an instance of Lanchester’s mathematical laws of strategy, as developed in WWI for fighting those hugely massive wings of German fighter planes. Net out– they would attack on the edges of the wing, where their small force would be mostly ignored by the large central force, but where according to Lanchester’s laws, they were assured by the mathematics that they could win– at least locally.
http://en.wikipedia.org/wiki/Force_concentration
So for example, by Lanchester’s laws it would be unwise to mass your forces of network theory teachers in Kansas. But according to those mathematical laws you could probably mass forces in Minnesota and win.
Then with the resulting larger force, use Lanchester’s laws to pick the next “critical target,” and so on. This mathematician I knew had data showing how in this manner the showrooms of the opposing force spread from outlying and comparatively insignificant areas of market share finally, in the last days, to invade Detroit itself.
Some thoughts about turning this into a ‘proper’ Markov process and estimating the rates.
In many Bayesian analyses, we’d like to use expert opinion to provide the prior distribution, and that is often difficult. The process is called ‘prior elicitation’. Experts in (say) urbanization are often not experts in probability theory. I am not convinced that “if the governance is good, how will this affect the population 10 years hence?” is the right question. Wouldn’t it need to have something like “if all other factors are held (magically) at fixed values” added? That might be really hard to do even if you are a joint expert in urbanization and probability theory.
The most useful parts of the matrix might actually be the white squares, since the rates are presumably zero there, so the number of parameters to be estimated is roughly halved.
I don’t think equilibria are going to be very useful to think about. The world is changing fast and is obviously a long way from equilibrium in the time scale (20-100 years) we are interested in. (Even if a non-trivial equilibrium exists, which I doubt.) It is maybe better to consider some looser concept like ‘persistent states’. Markov processes can get stuck for a long time in a region of state-space. I like the clouds visualization. There is a bigger visualization here of a Markov chain that I just saw today http://www.slideshare.net/erickmatsen/talk-31957869, slide 19. Not relevant to social change, but very pretty!
There is data available for estimating parameters. I don’t know where or what, but I think Hans Rosling does. http://www.ted.com/talks/hans_rosling_shows_the_best_stats_you_ve_ever_seen.
It seems we do have a good idea of the initial state say 10000 years ago. Thinking about that makes me think that some rates must be very small, or that time is ‘speeding up’, or something. Maybe we need to extend the model to have lots of countries. Presumably, a countries industrialise faster if they are in contact with industrialised countries, and so on.
Graham is correct that the judgment question includes (a) not knowing anything else about the developments of other system factors and (b) reporting whether one’s current belief about the most likely development of some target factor would change in light of certain information about the development of given factor
would change in light of certain information about the development of given factor  .
.
Additional thanks for recommending slide 19 of the Markov chain with 4096 trees! As part of the preliminary research that Alastair, I, and our team did, we considered a slightly more complicated toy model with 6 system factors resulting in 486 nodes. It was tricky to interpret the visualization. Alastair might have some ideas about how to start tackling this, but we’re very open to suggestions. For the IPCC studies I mentioned in my post, one of the networks had over 1700 nodes, while the other had over 1.5 million.
https://en.wikipedia.org/wiki/Accounting_information_system#Software_architecture_of_modern_AIS
It’s the Lanchester strategy.
I find it very interesting to see how (if i am reading the second matrix right) both urbanization and innovation affect many things, and how water scarcity is in turn affected by a lot of things.
Also interesting how education does affect many things indirectly through innovation.
I also wonder if an “inequality” dimension should be in the map, though you could make the case that it could fall within the “extreme poverty” and “economy” plane. It could be actually interesting to do an SVD (or actually even eigenvalue decomposition) to see which directions are the most important, just for fun. Probably somebody has done that already.
For example “innovation” and “technology change” could probably be collapsed into one dimension, while “coast population” does not seem very important.
Does anyone actually have a numeric model of this ?
I am thinking that these ideas can be applied to an experimental politics, to improve the human, and natural, condition of a nation.
If there is a federal republic, like USA, and union like UE with different states laws, then it is possible to think a continuous, and little, change of the states laws (year after year) so that it is possible to measure the change of the human, economic conditions (between different states); so that, after some time, there could be an improvement of the national laws (the reference laws). It is possible to think a worsening of some parameters, that can lead to an exploration of unexpected benefits from a political point of view, some complex behaviors that may be surprising (otherwise you don’t need a statistical study because it exist an optimal legislation).
If this is true, then a legislation is not static, and optimal, forever but it change for the parameters of the dynamical political system: economy, population grow, world condition and … global warming; but if this is true, the legislation statistically determined, from measured data, and there is not a political point of view that influence the choices (the little changes).
Vanessa Schweizer wrote:
The way this is formulated sounds as if this is some “observation” made after a calculation, which it isn’t – at least if I understood Alistair’s explanations correctly. That is these “properties” are asserted by the judgement of experts. In particular I could think of other judgements.
Like I don’t understand why there is automatically always no self-influence in your models, that is in Alastair’s explanation the diagonal was set to 0, or what else is meant by this? :
In particular I don’t see why for example a high population might not apriori lead to a lower population, that is if you have a high population density then this may lead to e.g. psychological factors which lead to a lowering of the population. One can of course say if a population is high then it stays high (or grows even higher), and that a replacement level population will stay constant and a low population with small birthrate will rather shrink or stay constant (that is what I understood is meant by a “perfect correlation” in your sense). But this is an assumption and should be noted as such.
nad is correct that these properties were uncovered through judgments of experts.
One has to read the full papers for the details (namely Schweizer & O’Neill as well as Lloyd & Schweizer), but these judgments were collected from demographers, economists, engineers, technologists, agricultural economists, etc. independently, so they had no awareness of what their colleagues were reporting for their judgments. It is striking that the independent judgments, when assembled in a cross-impact matrix, reveal this structure. This is why I speak of the pink highlighted rows as an observation.
Setting the diagonal to “meaningless” (which has the equivalent effect of setting it to 0) is indeed a methodological choice. A different choice could have been made in this regard, with an appropriate justification. For complex socio-economic systems, I think it is difficult to justify a priori why a particular outcome for a factor would necessarily reinforce or dampen its own outcomes. I think it is better to remove that kind of question (which is basically the diagonal) and let judgments for the other interacting factors do their work.
Nadja wrote:
The idea is that you quiz lots of different experts questions about correlations between different variables that they are experts on. No one expert knows the answers to all these questions. Then you notice that certain variables are highly correlated to many variables. This discovery may be a surprise to all the experts, since no one of them knew all the information you’ve assembled. In the case of ‘good governance’, it seems it actually was a surprise that this is highly correlated to many variables.
Of course the sort of discovery I’m talking about is only valid to the extent that the experts’ judgements are correct. It’s still a discovery, and potentially important.
This is a great example of why we need to be careful about the difference between ‘correlation at one moment in time’ and ‘correlation at different moments in time’.
The cross-impact balance analysis is about the former. The population being high now is perfectly correlated with the population being high now… so the diagonal entries of this matrix are obvious and uninteresting:
This is a separate question from whether and how the population now is correlated with the population later. That other question is interesting, but it’s not being studied in Vanessa’s example.
That’s why I wrote this:
Vanessa wrote:
Maybe I do not understand the sentence “The cross-impact balance study revealed this in the abstract, as summarized in the example matrices below.” in the right way. Since you do not usually reveal the result of a study in an abstract of an article (and if this was meant then which article?) I interpreted this sentence as that the matrices are regarded as an abstract representation of what is eventually in certain circles usually formulated in words. So I can’t find any hint in the text that this matrix summarizes actual real data and thus I interpreted it as an example (and that’s what Vanessa wrote: it is an example).
Is this matrix in some of the articles? I briefly scanned the two articles mentioned in Vanessa’s comment; it is not in there. Is it in the supplementary material? I do not have the time to read the articles.
Anyhow, even if this would be an overview over some studies, there might still be other studies, which would eventually turn some more rectangles grey. Like why should education not influence the economy?
John wrote:
I understand this, however Vanessa talks about “influence” (see above citation) and used the term “correlation” only for the diagonals in this example. There is quite a difference between correlation and influence. In particular she wrote in here that:
and omitted what to do about the diagonals unless I overread something.
Alastairs interpretation was also more in the direction of an active influence that is the experts judgements shall indicate a more likely state, i.e last but not least a change of a state.
But exerting an influence (at least in my way of understanding “influence”) would always be connected with time unless you don’t believe in general relativity.
????
So what is really meant here with this impact/influence/correlation?
If I get you right you think it is just correlation at one moment in time in all of the matrix.
But then what is this constraint in the example Alastair gave?
May it be that the interpretation of what the “expert’s judgements” are is eventually changing from case to case?
???
Nadja wrote:
Yes, I too don’t know what “in the abstract” means here. I hadn’t really noticed that part.
I also don’t know if these matrices were taken from an actual study or are merely intended as examples of what studies are likely to find.
Of course further studies might change the results; this is never surprising. Especially in anything involving sociology, we should expect that experts will disagree, studies will contradict each other, and people will argue a lot.
Of course almost everything influences almost everything else a little bit. So I took the white rectangles to mean that experts claim one factor has a small amount of direct influence on another
Admittedly, Vanessa wrote:
However, I don’t believe she really meant NO direct influence. I think she must have meant a ‘low amount’ of direct influence. This would be consistent with Alastair’s chart:
And of course, I don’t know exactly how much influence is a ‘low amount’. The use of phrases like ‘low’, ‘medium’ and ‘high’ could and should eventually be studied, but that’s not near the top of my own personal priorities.
I know what I like, and I’ve said that… but I’m not the one doing these cross-impact balance studies, so we should let some of those people tell us what they mean. (Obviously they may not agree!)
Yes, that’s what I think is the simplest approach: correlation at a given moment in time. We could also use other concepts.
I think it’s very important, when doing these studies, to be quite clear about what you’re trying to ask the experts, and do what it takes to make sure the experts answer the question you’re really asking.
People who design ‘expert systems’, and people who do opinion polling, have thought a lot about how to ask questions well. Without training in this art, it’s easy to get junk answers.
Graham wrote:
I agree. In my own personal theoretical ruminations I would like to avoid the important issue of how to ask questions that elicit useful answers, since I know nothing about this except that I know nothing about this. I would instead like to think about what to do with the answers once we’ve got them, since here I have a slight chance of contributing something useful.
I’m glad that the readers of Azimuth are sinking their teeth into this. Hopefully I can clarify some questions that have recently come up. In this long response, I discuss (1) semantic issues, (2) correlation, and (3) what to read/download in order to take a deeper dive into the example I discuss in my post.
First, semantics, namely use of the terms ‘impact’, ‘influence’, and ‘correlation’.
I am unfamiliar with specific mathematical definitions for the words ‘impact’ and ‘influence’. The operational meaning of these words in cross-impact analysis and related scenario analytic methods (i.e. structural analysis developed by Michel Godet, and cross-impact balances developed by Wolfgang Weimer-Jehle) is that the outcome of a given factor affects the outcome of a target factor.
An important distinction in cross-impact balances is that judgments about direct influences are recorded, while the algorithm calculates indirect influences. Other methods often do not make this distinction. This is why the white space in a cross-impact matrix does have a particular meaning.
Nadja asked:
“Like why should education not influence the economy?”
Here I must make a confession, as I am no better than Alastair (in fact, I am much worse). He had a typo in his matrix; in my matrix, I have some transcription errors. Educational outcomes should be exerting a direct influence on the economy (and population, and agricultural productivity, urbanization, extreme poverty, and quality of governance; but not on water scarcity. Clearly I did a poor job of proofreading this!).
Nevertheless, there is still a teaching moment in Nadja’s question. At times, judgments in a cross-impact balance matrix may appear to ‘leave out’ a set of influences that should be present. Often this is not necessarily the case, as one can trace the indirect influences of a factor by looking at the columns for other factors. In this way, cross-impact judgments convey just as John said:
“Of course almost everything influences almost everything else a little bit.”
More specifically, white space means that a factor exerts such a weak direct influence that it is negligible; however, it probably still exerts indirect influences, and judgments in the rest of the matrix would reflect this.
Before continuing on, I should address John’s question about whether these matrices are toy examples or are from real studies. They are from a real study (Schweizer & O’Neill 2014). However, I must now make a disclaimer that the matrix in my post should be treated as a toy example due to transcription errors.
Wrapping up the semantic discussion, there is the word ‘correlation’. I am agnostic about how important it is to split hairs over this word in a cross-impact balance analysis, since part of why the tool is used in the first place is that it is modelling observed or theorized relationships that have, so far, defied mathematical modelling for whatever reason. Some people like to use the word ‘correlation’ when talking about cross-impact judgments. I think it is fine to do so, since maybe after more research, it will be established that ‘what is really going on’ is a causal relationship, and not just a correlation. Alternatively, maybe some relationships we currently think are causal will be debunked later, so we go back to saying that two factors are correlated because that is the best we can do.
Moving on to the second topic — correlation as a concept — I found John’s distinction of the temporal aspects of correlation something to think about. His interpretation of the diagonal as reflecting factor outcomes that currently correlate with each other is straightforward and correct. However, we were asking experts how information about a certain future outcome for one particular factor would affect their judgment of the likely outcome (over the same time frame) for their target factor. Is this problematic? I’m not sure, since we’re asking the expert how a very specific piece of certain information affects their expectation (based on current knowledge) of how some other factor will behave.
For the third and final topic of taking a harder look at the example being discussed, any readers that want to do so will have to look at the Schweizer & O’Neill paper as well as supplementary information. It’s all written up there. See the main paper for a discussion of the cross-impact question; ESM1 for the raw judgments collected in cross-impact matrices for further analyses; ESM3 for definitions of factors (as well as the operational meanings of ‘low’, ‘medium’, and ‘high’) and a copy of the elicitation protocol; and ESM4 for empirical data on historical relationships that informed the alternative future projections featured in the elicitation protocol (i.e. the meanings of ‘low’, ‘medium’, and ‘high’).
Thanks for the good discussion!
Vanessa wrote:
I think you’re both great.
If either of you want to send me corrected matrices, I can easily fix them here.
Me too. Bayesian networks give a way to talk about one variable directly influencing another, but I guess they use the term ‘conditional dependency’, not ‘direct influence’.
I can use probability theory to understand a bunch about ‘correlation’, so I was—and am still—tempted to use probability theory to make the stochastic cross-balance analysis, and in particular the calculation of an equilibrium distribution for a Markov chain, into a mathematically clear process… by which I mean: something where I understand what we’re doing and why we’re doing it.
(Of course there’s a lot of fuzziness inherent in this business, but I still think it’s handy to have a mathematically clear story about what you would be doing if you were able to elicit certain probabilities from experts. I am perfectly happy to bracket that problem.)
Roughly my thought was something like this: given two variables x and y, we can talk about the probability that x takes some value given that y takes some value. Given all these, we can try to find a ‘self-consistent’ probability distribution on the values of all the variables. We might try to compute this by running a Markov chain to its equilibrium.
But now I see various flaws in my thinking. First of all, if you’re asking the experts about ‘direct’ influences, that’s not the same as ‘the probability that x takes some value given that y takes some value.’ The latter includes indirect effects.
Second, it’s very optimistic to hope that ‘ ‘the probability that x takes some value given that y takes some value’ is all we’d want to know, since there are lots of correlations involving more than 2 variables.
Luckily, dealing with these problems—separating causation from mere correlation, and separating ‘direct’ from ‘indirect’ causality, is the kind of thing people can tackle using Bayesian networks. So it’s not a hopeless business (especially since my student Brendan Fong has written about Bayesian networks).
Still, I’m hoping that we can make up some story using probability theory such that finding the equilibrium of a Markov chain obtained from the stochastic cross-impact balance method can be explained as finding the ‘unique probability distribution such that…’ where the ‘…’ is something both mathematically precise and conceptually interesting.
Even if we need some unrealistic simplifying assumptions about conditional probabilities to make this work, it would be good to know what those are. (E.g., maybe we’re assuming there’s some simple recipe to compute the probability that ‘if x takes some value and y takes some value then z takes some value’ from ‘if x takes some value then z takes some value’ and ‘if y takes some value then z takes some value’.)
John wrote:
So far the best story I can get is this.
We elicit information from experts that lets us define a discrete-time Markov chain on some finite set of scenarios. (Jamie’s blog post uses a continuous-time Markov chain, but this gives rise to a discrete-time Markov chain with the same equilibria, which I’ll find easier to work with here.)
If is the probability of the
is the probability of the  th scenario at the
th scenario at the  th time step, this Markov chain looks like
th time step, this Markov chain looks like
where is a matrix of transition probabilities—necessarily a stochastic matrix, meaning
is a matrix of transition probabilities—necessarily a stochastic matrix, meaning
for all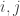 and
and
for all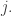
So, a probability distribution is an equilibrium for this Markov chain if
is an equilibrium for this Markov chain if
My questions are what does this Markov chain really mean? and what do these matrix elements really mean? In particular, the time steps in this Markov chain are most likely not about actual time in the real world.
really mean? In particular, the time steps in this Markov chain are most likely not about actual time in the real world.
In a rough sense measures how much being in the
measures how much being in the  th scenario increases the chance that we are in the
th scenario increases the chance that we are in the  th scenario. The equilibrium condition
th scenario. The equilibrium condition
is a kind of self-consistency condition, as hinted in the name ‘cross-impact balance’. The Markov chain may be just a method of finding choices of that obey this condition: we take any choice of
that obey this condition: we take any choice of  , we keep on evolving it via
, we keep on evolving it via
and we get closer and closer to an equilibrium. In this way of thinking, the time steps don’t have any significance of their own.
But my initial attempts to be more precise about the meaning of the coefficients as ‘correlations’—see above—didn’t quite make sense.
as ‘correlations’—see above—didn’t quite make sense.
I’m hoping that the condition
is an example of structural equation modelling, but I haven’t seen people do this modelling where the quantities involved are probabilities and they all influence each other!
John wrote, “My questions are what does this Markov chain really mean?”
If the attached diagram of (a) the equation in question to (b) the laboratory animal experiments called probability learning, is in fact a correct application of the equation, then one could perhaps compare this application in the lab experiment when studying the same questions in this very interesting social psychology experiment with experts.
https://docs.google.com/file/d/0B9LMgeIAqlIETWZOdmJxLTRoRmc/edit?usp=docslist_api
I really don’t understand why you bring up “probability learning” in response to almost everything I talk about here. It doesn’t seem relevant here, and you’re not explaining the relevance. In any case, I can’t access the link you provided.
It’s an experiment I know about. The diagram is “Petri nets of the Markov chains in probability learning for n=3.”
In it I use the equation about which you posed and emphasized a question in your previous comment.
Does this example of the equation address the question you had in mind?
I am thinking to the cross-impact balance like a real transition matrix for a Markov chain.

If an expert give a connection between values of the factors in the cross-impact balance, then the expert give a probability that the two values are connected by a graph, an arrow that connect the two factors, so that the cross-impact balance have a graph representation with value for each arrow (like Markov chain).
Here there is not a probability constraint on the factors, that can assume each value, so that the constraint on the transition values are not more true (it is not a probability).
The values are coarse, so that the value is not a true mathematical measure, it is like an interval (a measure with human error).
I don’t think that the matrix is constant in the time, because the cross-impact balance is a measure of a dynamical system.
It seem a differential equation, or a discrete equation, where the function is
and the parameter values are positive, or negative, values of experts: it can be a simple linear approximation of a slow dynamical system.
Domenico, “if an expert give a connection between values of the factors in the cross-impact balance, then the expert give a probability that the two values are connected by a graph, an arrow that connect the two factors, so that the cross-impact balance have a graph representation”
Yes, and from the graph in that google drive pdf, there is a “local logic” to it all. The percent of time that the token spends in a place, is by some sort of pattern, associative–
Imagine yourself as one of the states in a Markov chain, while other players in the game represent other unique states. But in this game, you only have one ball between you, and you pass it to each other.
Those passes of the ball are the links of the Markov chain.
The logic of these chains is that they link every player to every other player.
Say that after all is said in the round-up of the game by expert commentators,
that you, as one of the states in the Markov chain, had control of the ball X PERCENT of the total time the ball had been in play during the game.
What happens during the game is that the ball is tricky to hold onto. The average of unique possession by a player is like the quantum of the game. After that quantum of time, usually a different player wins the ball away from you.
There is an equation about it.
say the probability that you have control of the ball in the game is P.
Then the probability that you’ll hold onto it for two quanta of time in the game =
PP
where P is your rate of ball control in the game,
In the Petri net if the Markov chain in that diagram I posted on google drive, above, has the instances of these equations as ‘arrow to self’ in the diagram.
Domenico maybe this be one way to see Markov chains in game theory
I think that each dynamic can be seen in the game theory, and it is possible to reduce the time intervals of each dynamic to obtain discrete equation.
I try to formalize the cross-impact balance to give the expert the possibility to control the dynamic (for good purpose like here); but it is fun if the cross-impact balance have a dynamic, and the Markov chain have a dynamic, that it is an approximation of an autonomous system.
The theory is interesting because it seem to describe human state, like the happiness, sense of security, that can be evaluated with cross-impact balance analysis; this is good, because it is possible to improve the human lives, but all depends on the parameter types, and this permit to measure state of the psyche of a population (I think that some parameter choices are not ethical).
When I see the first matrix used in these studies, it seem to me an hazard, because if it is possible to measure correlation that can influence the inner state of a population, then it is possible to use in advertising (I think that in not codified way are used, with the use of woman body with sex in adversing, the leverage points, etc), and for climate change denial (I think that are used similar strategy) where there is not a strong scientific theory, or a strong numerical data to prove the theory, because the higher spending is not in the theory studies, but in the population manipulation: if a theory is true, then an increase in the study, and evaluation, can strenghten the theory, but I see that there is a contrast with each investment in these fields, why?
I think that it is not ethical to use the same means to obtain the same effect (influence on the population), but that it is ethical to understand what are the parameters that can help the people to undestand the climate change (graphics, simplified public relation, a single information strategy for different researchers).
Seemingly interesting study here on collapse of civilizations (whatever “collapse” might mean). I wonder what kind of model he used.
I noticed that article too! It says:
I looked for papers by Safa Motesharri and found only this:
• Safa Motesharri, Jorge Rivas and Eugenia Kalnay, A minimal model for human and nature interaction, 13 November 2012.
This describes the HANDY model, which turns out to be a set of 4 coupled ordinary differential equations. I’d like to blog about this, or get one of those authors to do so. Even if it’s oversimplified in various ways (which seems inevitable), it could be quite interesting!
As the saying goes, all models are wrong, some are useful :-)
The equations are explained very well in the paper, yes I for one would love to see a few blog posts about this model.