A few years ago, after hearing Susan Holmes speak about the mathematics of phylogenetic trees, I became interested in their connection to algebraic topology. I wrote an article about this here:
• John Baez, Operads and the tree of life, 6 July 2011.
In trying to the make the ideas precise I recruited the help of Nina Otter, who was then a graduate student at ETH Zürich. She came to Riverside and we started to work together.
Now Nina is a grad student at Oxford working on mathematical biology with Heather Harrington. I visited her last summer and we made more progress… but then she realized that our paper needed another big theorem, a result relating our topology on the space of phylogenetic trees to the topology described by Susan Holmes and her coauthors here:
• Louis J. Billera, Susan P. Holmes and Karen Vogtmann, Geometry of the space of phylogenetic trees, Advances in Applied Mathematics 27 (2001), 733–767.
It took another half year to finish things up. I could never have done this myself.
But now we’re done! Here’s our paper:
• John Baez and Nina Otter, Operads and phylogenetic trees.
The basic idea
Trees are important, not only in mathematics, but also biology. The most important is the ‘tree of life’ relating all organisms that have ever lived on Earth. Darwin drew this sketch of it in 1837:

He wrote about it in On the Origin of Species
The affinities of all the beings of the same class have sometimes been represented by a great tree. I believe this simile largely speaks the truth. The green and budding twigs may represent existing species; and those produced during former years may represent the long succession of extinct species. At each period of growth all the growing twigs have tried to branch out on all sides, and to overtop and kill the surrounding twigs and branches, in the same manner as species and groups of species have at all times overmastered other species in the great battle for life.
Now we know that the tree of life is not really a tree in the mathematical sense. One reason is ‘endosymbiosis’: the incorporation of one organism together with its genetic material into another, as probably happened with the mitochondria in our cells and also the plastids that hold chlorophyll in plants. Another is ‘horizontal gene transfer’: the passing of genetic material from one organism to another, which happens frequently with bacteria. So, the tree of life is really a thicket:

But a tree is often a good approximation, especially for animals and plants in the last few hundred million years. Biologists who try to infer phylogenetic trees from present-day genetic data often use simple models where:
• the genotype of each species follows a random walk, but
• species branch in two at various times.
These are called ‘Markov models’. The simplest Markov model for DNA evolution is the Jukes–Cantor model. Consider one or more pieces of DNA having a total of n base pairs. We can think of this as a string of letters chosen from the set {A,T,C,G}:
As time passes, the Jukes–Cantor model says the DNA changes randomly, with each base pair having the same constant rate of randomly flipping to any other. So, we get a Markov process on the set
However, a species can also split in two. So, given current-day genetic data from various species, biologists try to infer the most probable tree where, starting from a common ancestor, the DNA in question undergoes a random walk most of the time but branches in two at certain times.
To formalize this, we can define a concept of ‘phylogenetic tree’. Our work is based on the definition of Billera, Holmes and Vogtmann, though we use a slightly different definition, for reasons that will soon become clear. For us, a phylogenetic tree is a rooted tree with leaves labelled by numbers and edges labelled by ‘times’ or, geometrically speaking, ‘lengths’ in
We require that:
• the length of every edge is positive, except perhaps for ‘external edges’: that is, edges incident to the leaves or root;
• there are no 1-ary vertices.
For example, here is a phylogenetic tree with 5 leaves:

where but we demand that
We draw the vertices as dots. We do not count the leaves and the root as vertices, and we label the root with the number
We cannot collapse edges of length zero that end at leaves, since doing so would eliminate those leaves. Also note that the embedding of the tree in the plane is irrelevant, so this counts as the same phylogenetic tree:

In applications to biology, we are often interested in trees where the total distance from the root to the leaf is the same for every leaf, since all species have evolved for the same time from their common ancestor. These are mathematically interesting as well, because then the distance between any two leaves defines an ultrametric on the set of leaves. However, more general phylogenetic trees are also interesting—and they become essential when we construct an operad whose operations are phylogenetic trees.
Let be the set of phylogenetic trees with n leaves. This has a natural topology, which we explain in Section 6 of our paper. For example, here is a continuous path in
where we only change the length of one internal edge, reducing it until it becomes zero and we can collapse it:

Phylogenetic trees reconstructed by biologists are typically binary. When a phylogenetic tree appears to have higher arity, sometimes we merely lack sufficient data to resolve a higher-arity branching into a number of binary ones. With the topology we are using on binary trees form an open dense set of
except for
However, trees of higher arity are still important, because paths, paths of paths, etc. in
are often forced to pass through trees of higher arity.
Billera, Holmes and Vogtmann focused their attention on the set of phylogenetic trees where lengths of the external edges—edges incident to the root and leaves—are fixed to a constant value. They endow
with a metric, which induces a topology on
and there is a homeomorphism
where the data in describe the lengths of the external edges in a general phylogenetic tree.
In algebraic topology, trees are often used to describe the composition of n-ary operations. This is formalized in the theory of operads. An ‘operad’ is an algebraic stucture where for each natural number we have a set
whose elements are considered as abstract n-ary operations, not necessarily operating on anything yet. An element
can be depicted as a planar tree with one vertex and n labelled leaves:

We can compose these operations in a tree-like way to get new operations:

and an associative law holds, making this sort of composite unambiguous:

There are various kinds of operads, but in this paper our operads will always be ‘unital’, having an operation that acts as an identity for composition. They will also be ‘symmetric’, meaning there is an action of the symmetric group
on each set
compatible with composition. Further, they will be ‘topological’, meaning that each set
is a topological space, with composition and permutations acting as continuous maps.
In Section 5 we prove that there is an operad the ‘phylogenetic operad’, whose space of n-ary operations is
This raises a number of questions:
• What is the mathematical nature of this operad?
• How is it related to ‘Markov processes with branching’?
• How is it related to known operads in topology?
Briefly, the answer is that is the coproduct of
the operad for commutative topological semigroups, and
the operad having only unary operations, one for each
The first describes branching, the second describes Markov processes. Moreover,
is closely related to the Boardmann–Vogt
construction applied to
This is a construction that Boardmann and Vogt applied to another operad in order to obtain an operad whose algebras are loop spaces.
To understand all this in more detail, first recall that the raison d’être of operads is to have ‘algebras’. The most traditional sort of algebra of an operad is a topological space
on which each operation
acts as a
continuous map
obeying some conditions: composition, the identity, and the permutation group actions are preserved, and depends continuously on
The idea is that the abstract operations in
are realized as actual operations on the space
In this paper we instead need algebras of a linear sort. Such an algebra of is a finite-dimensional real vector space
on which each operation
acts as a multilinear map
obeying the same list of conditions. We can also think of as a linear map
where is the nth tensor power of
We also need ‘coalgebras’ of operads. The point is that while ordinarily one thinks of an operation as having n inputs and one output, a phylogenetic tree is better thought of as having one input and n outputs. A coalgebra of
is a finite-dimensional real vector space
on which operation
gives a linear map
obeying the same conditions as an algebra, but ‘turned around’.
The main point of this paper is that the phylogenetic operad has interesting coalgebras, which correspond to how phylogenetic trees are actually used to describe branching Markov processes in biology. But to understand this, we need to start by looking at coalgebras of two operads from which the phylogenetic operad is built.
By abuse of notation, we will use as the name for the operad having only unary operations, one for each
with composition of operations given by addition. A coalgebra of
is a finite-dimensional real vector space
together with for each
a linear map
such that:
• for all
•
• depends continuously on
Analysts usually call such a thing a ‘continuous one-parameter semigroup’ of operators on
Given a finite set a ‘Markov process’ or ‘continuous-time Markov chain’ on
is a continuous one-parameter semigroup of operators on
such that if
is a probability distribution on
so is
for all
Equivalently, if we think of
as a
matrix of real numbers, we demand that its entries be nonnegative and each column sum to 1. Such a matrix is called ‘stochastic’. If
is a set of possible sequences of base pairs, a Markov process on
describes the random changes of DNA with the passage of time. We shall see that any Markov process on
makes
into a coalgebra of
This handles the Markov process aspect of DNA evolution; what about the branching? For this we use the unique operad with one n-ary operation for each n > 0. Algebras of
are not-necessarily-unital commutative algebras: there is only one way to multiply n elements for n > 0.
For us what matters most is that coalgebras of are finite-dimensional cocommutative coalgebras, not necessarily with counit. If
is a finite set, there is a cocommutative coalgebra whose underlying vector space is
The unique n-ary operation of
acts as the linear map
where
This map describes the ‘n-fold duplication’ of a probability distribution on the set
of possible genes. We use this map to say what takes place when a species branches:

Next, we wish to describe how to combine the operads and
to obtain the phylogenetic operad. Any pair of operads
and
has a coproduct
The definition of coproduct gives an easy way to understand the algebras of
Such an algebra is simply an object that is both an algebra of
and an algebra of
with no compatibility conditions imposed.
One can also give an explicit construction of Briefly, the n-ary operations of
are certain equivalence classes of trees with leaves labelled
and all nodes, except for leaves, labelled by operations in
or
While this fact is surely known to experts on operads, it seems hard to find in the literature, so we prove this in Theorem 24.
Given this, it should come as no surprise that the operad is the coproduct
In fact, we shall take this as a definition. Starting from this definition, we work backwards to show that the operations of
correspond to phylogenetic trees. We prove this in Theorem 28. The definition of coproduct determines a topology on the spaces
and it is a nontrivial fact that with this topology we have
for n > 1, where
has the topology defined by Billera, Holmes and Vogtmann. We prove this in Theorem 34.
Using the definition of the phylogenetic operad as a coproduct, it is clear that given any Markov process on a finite set the vector space
naturally becomes a coalgebra of this operad. The reason is that, as we have seen,
is automatically a coalgebra of
and the Markov process makes it into a coalgebra of
Thus, by the universal property of a coproduct, it becomes a coalgebra of
We prove this in Theorem 36.
Since operads arose in algebraic topology, it is interesting to consider how the phylogenetic operad connects to ideas from that subject. Boardmann and Vogt defined a construction on operads, the ‘ construction’, which when applied to the operad for spaces with an associative multiplication gives an operad for loop spaces. The operad
has an interesting relation to
To see this, define addition on
in the obvious way, where
Then becomes a commutative topological monoid, so we obtain an operad with only unary operations, one for each
where composition is addition. By abuse of notation, let us call this operad
Boardmann and Vogt’s construction involves trees with edges having lengths in
but we can equivalently use
Leinster has observed that for any nonsymmetric topological operad
Boardmann and Vogt’s operad
is closely related to
Here we make this observation precise in the symmetric case. Operations in
are just like phylogenetic trees except that edges may have length
Moreover, for any operad
the operad
is a non-unital suboperad of
An operation of
lies in
if and only if all the external edges of the corresponding tree have length
We prove this in Theorem 40.
Berger and Moerdijk showed that if acts freely on
and
is well-pointed, then
is a cofibrant replacement for
This is true for
the operad whose algebras are topological semigroups. This cofibrancy is why Boardmann and Vogt could use
as an operad for loop spaces. But
does not act freely on
and
is not a cofibrant replacement for
So, it is not an operad for infinite loop spaces.
Nonetheless, the larger operad a compactification of
is somewhat interesting. The reason is that any Markov process
approaches a limit as Indeed,
extends uniquely to a homomorphism from the topological monoid
to
Thus, given a Markov process on a finite set
the vector space
naturally becomes a coalgebra of
We prove this in Theorem 38.

John,
This is very nice work. I can’t say that I understand all of it, but it reminds me of a story from about 30 years ago, when I had the privilege to meet a living legend.
It was the mid-1980’s when I went to a lecture at my university that featured the late, great Stephen Jay Gould. His vocabulary was so extensive that every time I tried to read something he wrote, I needed a companion dictionary to get through each paragraph. This article reminds me of SJG, the theory of punctuated equilibrium, and his unbelievable book titled the “The Structure of Evolutionary Theory.”
Fast forward about 30 years, and one day my three-year old asks me to read him a book. For a little lighter reading and to see the surprising choice of the book he selected, see this article: https://3danim8.wordpress.com/2015/10/08/what-should-you-do-when-your-3-yr-old-asks-you-to-read-this-book/
Re: “Biologists who try to infer phylogenetic trees from present-day genetic data” – Has anyone tried to define/quantify something like a ‘decay rate’ for this kind of information (e.g. an upper bound on the fraction of information that could possibly be inferred concerning the biosphere’s phylogenetic state x years in the past, as a function of x)?
I don’t know. Mathematicians have formulas for the rate at which information about the past decays as something changes randomly via a Markov process. So, one could take any Markov model of DNA evolution, plug in biologists’ favorite values of the constants involved, and compute the rate at which information decays. But I don’t know if someone has done this.
A good place to start would be here:
• E. Sober and M. Steel, Entropy increase and information loss in Markov models of evolution, Biol. Philos. 26 (2011), 223–250.
I bumped into this when finishing my paper with Blake Pollard, Relative entropy in biological systems. So, somehow all this work I’m doing is related, even if I don’t fully understand how.
Thank you John, I will look for that.
(I just realized btw that my question as phrased is a hybrid one, since a presumably small-but-important subset of the genetic info which is in principle available at a given time exists in already-dead organisms.
So to answer the Q, one must consider not only ‘evolutionary decay’ – the generation-over-generation loss of information concerning the biosphere’s phylogenetic state at a given earlier time due to evolutionary change – but also ‘physical decay’ – the degradation of genetic info in dead organisms.)
On the Azimuth Forum, I said:
John replied:
Even if I don’t need to worry about it, it might be interesting to think about it some more. I have spent most of 2015 inside tree-space, trying to find good ways of moving around it. Perhaps operad theory could inspire something at least. (By ‘tree-space’ I mean something like Phyln, but not anything precise. My tree-space is more complicated.)
On Wikipedia, it says “Algebras are to operads as group representations are to groups.” I know about group and group representations (or at least I did once). So if I am working in tree-space, it is like working with some set of matrices without realising they correspond to an abstract group which is quite familiar to group theorists. Is this a good analogy?
Knowing that phylogenetic trees are operations in an operad does not seem that interesting by itself. To me, it seem much more interesting when you start moving around, from one tree to another. Is that also the way you see it?
From the post: “The point is that while ordinarily one thinks of an operation f in O_n as having n inputs and one output, a phylogenetic tree is better thought of as having one input and n outputs.”
When working with phylogenetic trees, we look at things both ways. In particular, the main calculation of a likelihood starts at the tips and works towards the root using Felsenstein’s tree-pruning algorithm (https://en.wikipedia.org/wiki/Felsenstein's_tree-pruning_algorithm). For all I know, these calculations are in an algebra which is well-known to operad-theorists.
Mostly, biologists move around tree-space in search of the ‘best’ one (eg maximum likelihood estimate), or to sample the ‘good’ ones (eg sample the Bayesian posterior distribution over tree-space). These moves (sometimes confusing called operations) are jumps, not continuous moves, so they have probability zero of landing on a tree which is not binary. They are usually little jumps, so it’s not that different from moving around continuously.
Recently, I’ve been thinking about another way in which one phylogenetic tree turns into another. Consider n DNA sequences sampled from the same (diploid, sexually reproducing) species and align them. This sort of thing:
1: AAGTCATAAG
2: AGGTCATAAA
3: AAGTTATAAG
As you go along the alignment from left to right, each site (each column) has a phylogenetic tree representing its history. This is a ‘coalescent tree’ (https://en.wikipedia.org/wiki/Coalescent_theory). Due to recombination (https://en.wikipedia.org/wiki/Genetic_recombination) these trees can be different. So going along the genome means exploring Phyln. This is also a series of little jumps. This seems to bring operads even closer to reality.
Graham wrote:
True. Brian Eno recently defined “culture” to be “everything we don’t need to do”.
It’s a good analogy. To make the analogy really precise, we could say
A group is a set with a multiplication, identity and inverses. A representation of
with a multiplication, identity and inverses. A representation of  maps each element of
maps each element of  to an
to an 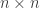 matrix in such a way that multiplication, identity and inverses in the group get sent to multiplication, identity and inverses in the world of matrices.
matrix in such a way that multiplication, identity and inverses in the group get sent to multiplication, identity and inverses in the world of matrices.
The phylogenetic operad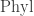 is a big set of all trees with edges labelled by lengths. But it’s not just a set: it has operations that say how to glue one tree onto another. This is why it’s an ‘operad’. A Markov model maps each tree to a matrix that describes how a probability distribution on the genome data of the species at the root of the tree stochastically evolves to a probability distributions on the genome data of the descendant species at the leaves. Ways of gluing trees together get sent to ways of combining these matrices.
is a big set of all trees with edges labelled by lengths. But it’s not just a set: it has operations that say how to glue one tree onto another. This is why it’s an ‘operad’. A Markov model maps each tree to a matrix that describes how a probability distribution on the genome data of the species at the root of the tree stochastically evolves to a probability distributions on the genome data of the descendant species at the leaves. Ways of gluing trees together get sent to ways of combining these matrices.
(I’m being quite rough here, just to get the point across with a minimum of distraction.)
Of course this is not be how you usually think of a Markov model—like the Jukes–Cantor model, for example. But we show it’s equivalent.
I see what you mean, but you’re more practical than me: I can get interested by things for very abstract reasons.
In particular, I love operads, and I know a lot of stuff about operads, because they’re really important in pure math. So, it was really interesting to meet an operad that’s a lot like some of the most important operads in math, but coming from genomics, where nobody had even noticed it was an operad!
It’s a bit like discovering a new group that so far was only implicitly used by ornithologists—who of course know nothing about group theory. For example, imagine that the symmetry group of an ostrich egg turned out to be a new finite simple group, one that had been overlooked by the mathematicians!
The operad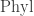 is not just any old operad: it’s one that arises very naturally in the theory of operads! It admits a quick one-sentence description, which any good operad theorist will understand (but nobody else). It’s closely connected to some operads that play a fundamental role in algebraic topology, and yet it’s never been discussed there, as far as I know. So that’s what our paper is mainly about.
is not just any old operad: it’s one that arises very naturally in the theory of operads! It admits a quick one-sentence description, which any good operad theorist will understand (but nobody else). It’s closely connected to some operads that play a fundamental role in algebraic topology, and yet it’s never been discussed there, as far as I know. So that’s what our paper is mainly about.
When it comes to “moving around”, part of the definition of an operad is that there’s a topology on each space of n-ary operations. In the case of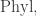 this space is called
this space is called 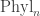 , and it’s a space of trees with n leaves, with edges labelled by ‘lengths’. (Again this is rough.) Thanks to this topology we can talk about a continuous path in this space of trees, which is what I (but not quite you) would mean by “moving around tree-space”. For example:
, and it’s a space of trees with n leaves, with edges labelled by ‘lengths’. (Again this is rough.) Thanks to this topology we can talk about a continuous path in this space of trees, which is what I (but not quite you) would mean by “moving around tree-space”. For example:
is a path in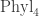 . As we move along this path, most of the time the tree stays the same and only the lengths of edges change. But at certain moments the tree changes.
. As we move along this path, most of the time the tree stays the same and only the lengths of edges change. But at certain moments the tree changes.
To bridge the gap between what I’m thinking about and what you think about, you might enjoy the introductory parts of this paper:
• Louis J. Billera, Susan P. Holmes and Karen Vogtmann, Geometry of the space of phylogenetic trees, Advances in Applied Mathematics 27 (2001), 733–767.
Billera, Holmes and Vogtmann describe the topology of or actually the smaller space
or actually the smaller space 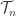 where the lengths of external edges are fixed to a constant value. They describe a metric, or distance function, on
where the lengths of external edges are fixed to a constant value. They describe a metric, or distance function, on 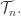 Moreover, they seem to have some idea about why biologists should care! More of an idea than I do, at least.
Moreover, they seem to have some idea about why biologists should care! More of an idea than I do, at least.
It’s interesting that their topology on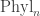 , which while ‘obvious’ takes some work to describe, also emerges naturally from the beautiful one-setence description of the operad
, which while ‘obvious’ takes some work to describe, also emerges naturally from the beautiful one-setence description of the operad 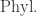
I would like to find ways that my work with Nina could be useful… while still doing beautiful math, preferably related to operads. It would probably involve taking ideas from biology—maybe some of the ideas you’re talking about—and thinking about them with more of an emphasis on how big trees are made of smaller trees. Building big trees from smaller ones is ‘composition’ in the operad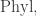 and composition is the main thing that makes an operad be an operad.
and composition is the main thing that makes an operad be an operad.
Thanks, John. The main thing I learnt was that composability is the key thing about operads (whereas I was thinking vaguely of topology, metric, or measure).
Actually, that is very much how I think about phylogenetic analysis as a whole. Except, upside down and inside out.
We start with probability distributions on the genome data of the descendant species at the leaves. These are what we observe in the DNA of various present-day organisms. (Usually these are regarded as known sequences, ie, as points rather than distributions, but that’s for computational efficiency not realism.) Then using Felsenstein’s tree-pruning algorithm, we work recursively back to the root, calculating vectors in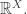 (The vectors are called ‘conditional likelihoods of subtrees’ or ‘partial likelihoods’.) An extra step at the root converts the vector there to a number, which is the probability of the observed data, given the tree. In other words, it is the likelihood of the tree, given the observations. The likelihood of the tree, given the observations, is The Central Object of study in phylogenetics analysis (though I don’t suppose many biologists would put it that way!).
(The vectors are called ‘conditional likelihoods of subtrees’ or ‘partial likelihoods’.) An extra step at the root converts the vector there to a number, which is the probability of the observed data, given the tree. In other words, it is the likelihood of the tree, given the observations. The likelihood of the tree, given the observations, is The Central Object of study in phylogenetics analysis (though I don’t suppose many biologists would put it that way!).
The formula for a single step in the calculation looks like this. Suppose a vertex in the tree has
in the tree has  children, which have vectors
children, which have vectors  , and the branches between
, and the branches between  and its children have lengths
and its children have lengths 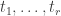 . Suppose
. Suppose  is a
is a 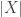 by
by 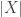 infinitesimal stochastic matrix which gives the rates at which members of
infinitesimal stochastic matrix which gives the rates at which members of  turn into one another. Then we make
turn into one another. Then we make  vectors
vectors  , and multiply these element-wise to make the vector at
, and multiply these element-wise to make the vector at  .
.
This seems the best bet for finding something that interests me into something ‘operadic’.
I already knew the Billera-Holmes-Vogtmann paper. And yes, that does seem about halfway between you and me. As I read it, their main reason why biologists should care is that it provides (in principle) ways of summarising The Central Object.
Thanks!
Right. An operad is a bunch of operations that you can compose. I attempted to say this in the blog article:
The formula you mention here:
is implicit in some stuff discussed in our paper, and even in the blog article here—though we were hiding it amid clouds of jargon, to make certains sorts of mathematician able to understand it better. The idea, as we see it, is that the phylogenetic operad is built from two simpler ones:
• one called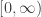 that describes time evolution, where the genome randomly changes according to a Markov process,
that describes time evolution, where the genome randomly changes according to a Markov process,
and
• one called that describes branching, where the genome gets duplicated, or ‘n-plicated’.
that describes branching, where the genome gets duplicated, or ‘n-plicated’.
Technically the phylogenetic operad is the ‘coproduct’ of these two other operads.
of these two other operads.
Of course I’m not claiming this viewpoint is better for normal humans.
You said earlier that the phylogenetic trees you consider are more fancy than the ones we consider. Maybe if you explained them to me I could see if they were operations in a mathematically interesting operad. (I can’t promise to do anything more useful than that.)
By the way, I fixed your LaTeX: when you post a comment there are instructions directly above that say how to use LaTeX here, but almost nobody ever reads them. In the process I took the liberty of changing “stochastic” to “infinitesimal stochastic”. A stochastic matrix is one that describes a finite amount of time evolution for a Markov process: namely, a square matrix of nonnegative numbers where the columns sum to 1. We need some other name for a matrix such that
such that  is stochastic for all
is stochastic for all 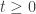 . Some people call this an intensity matrix or stochastic Hamiltonian. But I really want an adjective: I can’t grammatically say “now let us prove that this matrix is intensity”. Also, since in physics one speaks of the Hamiltonian of a particular physical system, one should not also use that word to denote a matrix with particular mathematical properties.
. Some people call this an intensity matrix or stochastic Hamiltonian. But I really want an adjective: I can’t grammatically say “now let us prove that this matrix is intensity”. Also, since in physics one speaks of the Hamiltonian of a particular physical system, one should not also use that word to denote a matrix with particular mathematical properties.
So, I use the adjective infinitesimal stochastic to denote a matrix such that is stochastic for all
is stochastic for all 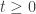 . This goes along with a tradition where we think of
. This goes along with a tradition where we think of  as describing an ‘infinitesimal’ amount of time evolution, and
as describing an ‘infinitesimal’ amount of time evolution, and 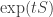 as describing a ‘finite’ amount of time evolution.
as describing a ‘finite’ amount of time evolution.
That’s fine, I don’t have much hope this is going to lead anywhere very useful. It might give me a different way of looking at something.
I am working with the multispecies coalescent model. This model has a bunch of ‘gene trees’ sitting inside a species tree. The individual trees are quite ordinary, but the gene trees are constrained by the species tree. There are some pictures (Figs 1 and 9) in this paper: http://mbe.oxfordjournals.org/content/27/3/570.full. The model incorporates a simple model from population genetics along each branch of the species tree.
The trees are binary and ultrametric. The tips of the species tree are labelled with species. I’ll just talk about a single gene tree. They are all basically the same sort of thing, so if you understand one gene tree, you understand them all. The gene tree will have at least as many tips as the species tree, usually more. At the tips are DNA sequences which have been sampled from individuals belonging to one of the species. The constraint is that going back in time, two DNA sequences cannot meet (coalesce) until the species they belong to have met.
A more biological description. Suppose you have two human DNA sequences for a particular gene. (You can generally get two sequences from each individual organism so they could be from the same person.) Suppose the human population is 50,000. That might sound crazy given the current population, but over the last six million years it is a reasonable guess. That means 100,000 copies in the human gene pool, and so using a very simple model of population genetics, the probability that this pair meets is 1/100,000 per generation, say 25 years. So the probability they have not met by six million years into the past is about exp(-6/2.5) or 9%. If they don’t meet, it is an example of ‘incomplete lineage sorting’. Once they’re back that far, they can meet DNA sequences from chimps. It means that a gene tree can have a different topology to the species tree.
I knew about the latex thing, and even put one ‘latex’ into my post. Then I got distracted by something else, and clicked on post before adding the rest. ‘infinitesimal stochastic’ is fine. Biologists just say ‘rate matrix’.
Dear John,
You might be interested in smooth blowup of the Billera-Holmes-Vogtmann model for tree space described in
• Navigation in tree spaces, Adv. Appl. Math. 67 (2015), 75–95.
It’s also connected to operads (more precisely, to the Deligne-Mumford-Knudsen operad defined by genus zero real algebraic curves); its spaces are aspherical, with an interesting (system of) fundamental group(s), analogous in some ways to the operad defined by the braid groups. It has an intrinsic pseudometric, with wall-crossing phenomena that look suspiciously biological…
Best, sincerely
Cool! I’ll check it out.
Hi John, This is a wonderful work. I met Nina when she visited SJSU, a few weeks ago. I talked to her and also briefly talked about my work. I am working on the relationship between C-sets and phylogenetics. Look forward to hearing more. Regards, Shabeena
Last year I became a bit obsessed with the shuffle multiplication resp. unshuffle coproduct. Do you have any use for it?
It appears in many branches of maths incl. operads (Loday/Vallette: Algebraic Operads – of which I know nothing) and Markov chains (Persi Diaconis). But it has not been explicitly appreciated in tensor calculus (Veblen already used it implicitly) – which I plan to change…
I used unshuffles in my work on Lie 2-algebra, and one needs shuffles to make the tensor algebra of vector space into a bialgebra. But I haven’t been shuffling much lately.
There are some nice comments about operads and phylogenetic trees over on the n-Category Café, including a nice approach to trees by Joachim Kock.