In the 1980s, the mathematician Ronald Graham asked if it’s possible to color each positive integer either red or blue, so that no triple of integers 
all have the same color. He offered a prize of $100.
Now it’s been solved! The answer is no. You can do it for numbers up to 7824, and a solution is shown in this picture. But you can’t do it for numbers up to 7825.
To prove this, you could try all the ways of coloring these numbers and show that nothing works. Unfortunately that would require trying
3 628 407 622 680 653 855 043 364 707 128 616 108 257 615 873 380 491 654 672 530 751 098 578 199 115 261 452 571 373 352 277 580 182 512 704 196 704 700 964 418 214 007 274 963 650 268 320 833 348 358 055 727 804 748 748 967 798 143 944 388 089 113 386 055 677 702 185 975 201 206 538 492 976 737 189 116 792 750 750 283 863 541 981 894 609 646 155 018 176 099 812 920 819 928 564 304 241 881 419 294 737 371 051 103 347 331 571 936 595 489 437 811 657 956 513 586 177 418 898 046 973 204 724 260 409 472 142 274 035 658 308 994 441 030 207 341 876 595 402 406 132 471 499 889 421 272 469 466 743 202 089 120 267 254 720 539 682 163 304 267 299 158 378 822 985 523 936 240 090 542 261 895 398 063 218 866 065 556 920 106 107 895 261 677 168 544 299 103 259 221 237 129 781 775 846 127 529 160 382 322 984 799 874 720 389 723 262 131 960 763 480 055 015 082 441 821 085 319 372 482 391 253 730 679 304 024 117 656 777 104 250 811 316 994 036 885 016 048 251 200 639 797 871 184 847 323 365 327 890 924 193 402 500 160 273 667 451 747 479 728 733 677 070 215 164 678 820 411 258 921 014 893 185 210 250 670 250 411 512 184 115 164 962 089 724 089 514 186 480 233 860 912 060 039 568 930 065 326 456 428 286 693 446 250 498 886 166 303 662 106 974 996 363 841 314 102 740 092 468 317 856 149 533 746 611 128 406 657 663 556 901 416 145 644 927 496 655 933 158 468 143 482 484 006 372 447 906 612 292 829 541 260 496 970 290 197 465 492 579 693 769 880 105 128 657 628 937 735 039 288 299 048 235 836 690 797 324 513 502 829 134 531 163 352 342 497 313 541 253 617 660 116 325 236 428 177 219 201 276 485 618 928 152 536 082 354 773 892 775 152 956 930 865 700 141 446 169 861 011 718 781 238 307 958 494 122 828 500 438 409 758 341 331 326 359 243 206 743 136 842 911 727 359 310 997 123 441 791 745 020 539 221 575 643 687 646 417 117 456 946 996 365 628 976 457 655 208 423 130 822 936 961 822 716 117 367 694 165 267 852 307 626 092 080 279 836 122 376 918 659 101 107 919 099 514 855 113 769 846 184 593 342 248 535 927 407 152 514 690 465 246 338 232 121 308 958 440 135 194 441 048 499 639 516 303 692 332 532 864 631 075 547 542 841 539 848 320 583 307 785 982 596 093 517 564 724 398 774 449 380 877 817 714 717 298 596 139 689 573 570 820 356 836 562 548 742 103 826 628 952 649 445 195 215 299 968 571 218 175 989 131 452 226 726 280 771 962 970 811 426 993 797 429 280 745 007 389 078 784 134 703 325 573 686 508 850 839 302 112 856 558 329 106 490 855 990 906 295 808 952 377 118 908 425 653 871 786 066 073 831 252 442 345 238 678 271 662 351 535 236 004 206 289 778 489 301 259 384 752 840 495 042 455 478 916 057 156 112 873 606 371 350 264 102 687 648 074 992 121 706 972 612 854 704 154 657 041 404 145 923 642 777 084 367 960 280 878 796 437 947 008 894 044 010 821 287 362 106 232 574 741 311 032 906 880 293 520 619 953 280 544 651 789 897 413 312 253 724 012 410 831 696 803 510 617 000 147 747 294 278 502 175 823 823 024 255 652 077 422 574 922 776 413 427 073 317 197 412 284 579 070 292 042 084 295 513 948 442 461 828 389 757 279 712 121 164 692 705 105 851 647 684 562 196 098 398 773 163 469 604 125 793 092 370 432
possibilities. But recently, three mathematicians cleverly figured out how to eliminate most of the options. That left fewer than a trillion to check!
So they spent 2 days on a supercomputer, running 800 processors in parallel, and checked all the options. None worked. They verified their solution on another computer.
This is one of the world’s biggest proofs: it’s 200 terabytes long! That’s about equal to all the digitized text held by the US Library of Congress. There’s also a 68-gigabyte digital signature—sort of a proof that a proof exists—if you want to skim it.
It’s interesting that these 200 terabytes were used to solve a yes-or-no question, whose answer takes a single bit to state: no.
I’m not sure breaking the world’s record for the longest proof is something to be proud of. Mathematicians prize short, insightful proofs. I bet a shorter proof of this result will eventually be found.
Still, it’s fun that we can do such things. Here’s a story about the proof:
• Evelyn Lamb, Two-hundred-terabyte maths proof is largest ever, Nature, May 26, 2016.
and here’s the actual paper:
• Marijn J. H. Heule, Oliver Kullmann and Victor W. Marek, Solving and verifying the Boolean Pythagorean triples problem via cube-and-conquer.
The ‘cube-and-conquer’ paradigm is a “hybrid SAT method for hard problems, employing both look-ahead and CDCL solvers”. The actual benefit of this huge proof is developing such methods for solving big problems! Roberto Bayardo explained:
CDCL == “conflict-directed clause learning”: when you hit a dead end in backtrack search, this is the process of recording a (hopefully small) clause that prevents you from making the same mistake again…a type of memorization, essentially.
Look-ahead: in backtrack search, you repeat the process of picking an unassigned variable and then picking an assignment for that variable until you reach a “dead end” (upon deriving a contradiction). Look-ahead involves doing some amount of processing on the remaining formula after each assignment in order to simplify it. This includes identifying variables for which one of its assignments can be quickly eliminated. “Unit propagation” is a type of look-ahead, though I suspect in this case they mean something quite a bit more sophisticated.
A much longer proof
By the way, despite the title of the Nature article, Michael Nielsen has pointed out a much longer proof by Chris Jefferson, who wrote:
Darn, I had no idea one could get into the media with this kind of stuff.
I had a much larger “proof”, where we didn’t bother storing all the details, in which we enumerated 718,981,858,383,872 semigroups, towards counting the semigroups of size 10.
Uncompressed, it would have been about 63,000 terabytes just for the semigroups, and about a thousand times that to store the “proof”, which is just the tree of the search.
Of course, it would have compressed extremely well, but also I’m not sure it would have had any value, you could rebuild the search tree much faster than you could read it from a disc, and if anyone re-verified our calculation I would prefer they did it by a slightly different search, which would give us much better guarantees of correctness.
His team found a total of 12,418,001,077,381,302,684 semigroups of size 10. They only had to find 718,981,858,383,872 by a brute force search, which is 0.006% of the total:
• Andreas Distler, Chris Jefferson, Tom Kelsey, and Lars Kottho, The semigroups of order 10, in Principles and Practice of Constraint Programming, Springer Lecture Notes in Computer Science 7514, Springer, Berlin, pp. 883–899.
Insanely long proofs
All the proofs mentioned so far are downright laconic compared to those discussed here:
• John Baez, Insanely long proofs, 19 October 2012.
For example, if you read this post you’ll learn about a fairly short theorem whose shortest proof using Peano arithmetic contains at least
symbols. This is so many that if you tried to write down the number of symbols in this proof—not the symbols themselves, but just the number of symbols—in ordinary decimal notation, you couldn’t do it if you wrote one digit on each proton, neutron and electron in the observable Universe!
Azimuth 
One can’t help noticing that the two-coloring illustrated above has three colors. Are the white cells “don’t care”s because those numbers are not members of any Pythagorean triples?
If so, then the bignum that you show us (2^7825) is much too big.
Yes, there are many ways to simplify the problem, of which this is probably the first. Another super-obvious one is that if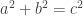
, then we must have 
mod 2. So, for example, we never need to worry about the case where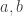 
and 
are all odd. At the end, Heule, Kullmann and Marek wound up needing to check fewer than a trillion colorings.
Yes. You can see that 1 and 2 are colored white, while 3 is colored blue.
Could they also be “don’t cares” because coloring them either blue or red will still result in a solution? If I am reading the figure right, both 4 and 6 are white. But, given that 3 is blue and 5 is red, it doesn’t matter what color 4 takes on.
If 4 is white then you must be right: it shows up in a Pythagorean triple, but it’s a “don’t care”.
In the spirit of “the other cases are left as an exercise”, I’m more interested (at this point) in the size of the program that checked all those colourings.
There’s a lot of information about the software in the paper itself:
• Marijn J. H. Heule, Oliver Kullmann and Victor W. Marek, Solving and verifying the Boolean Pythagorean triples problem via cube-and-conquer.
I didn’t see a single number giving the total length of all the programs used.
Curious what epistemic status people here apply to SNARKs.
E.g. https://eprint.iacr.org/2014/595 . You can compress a computation trace of any reasonable length to a constant 374 byte string, such that given the string it is possible to verify in constant time (about 30 msecs) that either the generator performed the computation as described, or else that it violated certain computational assumptions. (said assumptions are not post-quantum secure, and there’s a constant factor slowdown of roughly 10^11)
So, presumably nobody here has requested a copy of either the 200 TB or the 68 GB version and verified it themselves. If they had published a 374 byte SNARK (ignoring the implausible amount of computation it would take to generate by known techniques), how would that change the status of the result?
Looks like we now have non-galactic SNARKs under Minicrypt-level assumptions, if anyone is still reading: http://ia.cr/2016/646
What is a “non-galactic” SNARK?
I am referring to https://rjlipton.wordpress.com/2010/10/23/galactic-algorithms/ , which apparently isn’t standard terminology, whoops.
SNARKs can be generically constructed from probabilistically checkable proofs and Merkle trees, but I’ve heard that early versions of the PCP theorem had O(Bekenstein entropy of the galaxy) constant factors. Having trouble finding a citation for that right now though.
I see. Thanks!
In the binary red/blue assignment tree implied by this problem, has anyone graphed the fraction of ‘live’ nodes (ones representing solutions at the present level) for each of the first 7825 levels? (I think I see that since only live nodes have live children, this fraction never increases; still it would be interesting to see the variability and the general trend).
That would be nice to see, but I’ve never seen such a graph, and clearly toward the end (i.e. as we approach the number 7825) it becomes a huge amount of work.
FWIW rough-estimating the number of white squares in the illustrated solution config seems to imply over 10^800 solutions at level 7824. And I gather from section 3.6 in the paper that there are more level-7824 solution configs than that, possibly many more.
Which counted for little, as these teeming multitudes were laid low by just five numbers: 5180 & 5865, 625 & 7800, and 7825. That’s because, by level 7824 (and I guess by earlier than that, as a just-in-time one-two punch* seems too coincidental), the first pair of the five had been forced to a different color than the second pair in any solution configuration; and since each pair makes a Pythagorean triple with 7825, and 7825 can’t avoid both colors at once, that was all she wrote, billy goat.
*ok, 7824-7825 punch (so picky:-)
I have no problem with proofs that are “large” in this way. Presumably their program is not very big, and easy to verify. Likewise for their clever work to cut down the problem space to just a trillion cases to check.
The more problematic “large proofs”, to me, are those like Wiles’ proof of Fermat — 150 pages long, and so complex that only a handful of people in the world can understand it all. Mistakes were found in it before. I’m a programmer, and I certainly cannot write 150 pages of material in my field with zero mistakes. Can anyone?
Even Knuth, so methodical that he sends money to people who find mistakes in his work, has mailed over 100 checks for mistakes in his 2000-page seminal work. Despite taking literally decades to write and edit, he can’t go 20 pages without a minor blooper slipping through, in material that he already understands.
What confidence do we have that long and complex proofs are valid?
Ted wrote:
What confidence do we have that a complicated machine like a modern airplane, with thousands of parts, won’t malfunction and send us crashing to our deaths? It’s pretty much the same kind of question. Sometimes airplanes do malfunction and crash, yet I routinely use them and rarely worry about it, because the chance is high that I’ll safely reach my destination, because lots of people work very hard to make them safe.
It’s also worth noting that most mistakes in proofs can be easily fixed or sidestepped. This is a difference between proofs and programs. Something as trivial as a typo can prevent a program from working the way it should. But human mathematicians can easily bounce back from typos or even more significant mistakes as long as the overall idea of a proof is sound. So we don’t need ‘zero mistakes’. We just need zero mistakes that are hard to fix.
Finally, about Wiles’ proof. Around 1982–1986, Gerhard Frey and Ken Ribet showed that Fermat’s Last Theorem would follow from the ‘modularity conjecture’. This was a statement about geometry that a bunch of famous mathematicians were already interested in: it’s vastly more important than whether some goofy equation has integer solutions. Wiles proved a special case of the modularity conjecture, just enough to get Fermat’s Last Theorem. His first proof had a mistake; then his grad student Richard helped him fix it, and they published it in 1995. Then a bunch of people streamlined his argument and proved the full-fledged version of what is now called the Modularity Theorem. There have been conferences on this topic, and some textbooks as well. So by now many more than a handful of people have checked through this stuff.
Not me personally, but then I’m not a number theorist!
FWIW, according to my calculations the largest connected component of the graph (where vertices are members of Pythagorean triples and edges indicate they belong to the same triple) up to 7825 has 5482 vertices (including 7825 itself of course). I’m surprised this was not mentioned in the paper.
Wow, are you doing a lot of calculations in this topic?
No, I just once solved some Project Euler problems, and a few of them were about Pythagorean triples. I spent a few minutes on writing a script to generate all the triples and their multiples using Euclid’s formula and generate the graph (list of connected components really) from these. That’s a sub-second computation.