Some of us just finished a paper clarifying the connection between two approaches to describing open systems—that is, systems that can interact with their environment, and can be composed to form larger open systems:
• John Baez, Kenny Courser and Christina Vasilakopolou, Structured versus decorated cospans.
And, next week I’m giving a talk about it at YAMCaTS! This is not a conference for felines who like sweet potatoes: it’s the Yorkshire and Midlands Category Seminar, organized by Simona Paoli, Nicola Gambino and Steve Vickers.
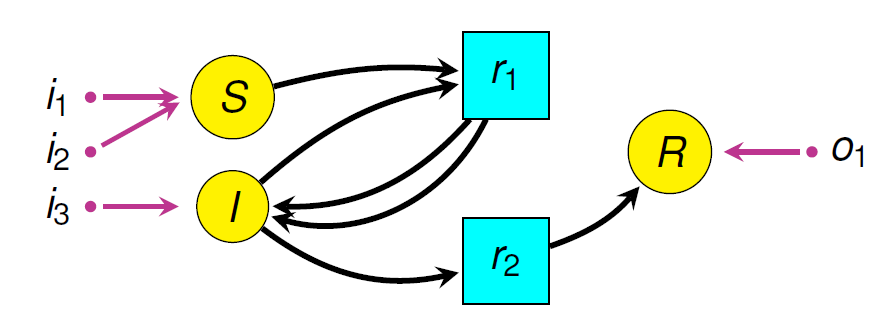
In my talk, I’ll start by sketching some ideas behind Halter and Patterson’s software for quickly assembling larger models of COVID-19 from smaller models. Then, I’ll dig deeper into the underlying math, where we use ‘structured’ or ‘decorated’ cospans to model open systems.
This quickly gets into some serious category theory—and since YAMCaTS is a category theory seminar, I won’t shy away from that. Here are my slides:
• John Baez, Structured vs decorated cospans, YAMCaTS, Friday 5 February 2021, 17:00 UTC. Zoom link here, meeting ID 810 4239 7132; to get in use 68302x where x is a one-digit perfect number.
Abstract. One goal of applied category theory is to understand open systems: that is, systems that can interact with the external world. We compare two approaches to describing open systems as cospans equipped with extra data: structured and decorated cospans. Each approach provides a symmetric monoidal double category, and we prove that under certain conditions these symmetric monoidal double categories are isomorphic. We illustrate these ideas with applications to dynamical systems and epidemiological modeling. This is joint work with Kenny Courser and Christina Vasilakopoulou.
I don’t know if my talk will be recorded, but it will be on Zoom so recording it would be easy, and I’ll try to get the organizers to do that.
For videos and slides of two related talks go here:
• Structured cospans and double categories.
• Structured cospans and Petri nets.
For more, read these:
• Evan Patterson and Micah Halter, Compositional epidemiological modeling using structured cospans.
• John Baez and Kenny Courser, Structured cospans.
• Kenny Courser, Open Systems: a Double Categorical Perspective. (Blog articles here.)
• Michael Shulman, Framed bicategories and monoidal fibrations.
• Joe Moeller and Christina Vasilakopolou, Monoidal Grothendieck construction.
To read more about the network theory project, go here: