Tuning systems in music is the subject where you get mad at irrational numbers. Nothing works perfectly—and it’s not your fault: it’s math’s fault. You’re left pushing around lumps in the carpet.
An ‘octave’ is the chord where the high note vibrates 2 times as fast as the low note. In a ‘perfect fifth’ it vibrates 3/2 times as fast. In a ‘perfect fourth’ it vibrates 4/3 as fast. In a ‘major third’ it vibrates 5/4 as fast. Our ears love these simple fractions.
But if you go up 4 perfect fifths, it’s not quite the same as going up 2 octaves and a major third, since
is not quite
AARGH! 😠
The ratio of these:
is called the syntonic comma.
Listen to two notes with this frequency ratio. You can hear they aren’t in tune, and it probably sounds annoying. This is why we can’t have nice things.
Another problem is that if you go up 7 octaves it’s almost but not quite 12 perfect fifths, since
is not
The ratio of these is called the Pythagorean comma:
This is why a 12-tone scale with all the notes equally spaced can’t have perfect fifths. But for vocal music, the syntonic comma is more urgent problem, since it involves simpler fractions. It shows up in lots of different ways: two people can sing two different parts starting in tune, each singing beautifully, and wind up out of tune.
For example, say you try to sing
First you go up a fifth. Then you go down a fourth. Then you go up a fifth again. Then you go down a fourth again. Then you go down a major third. Are you back where you started? No, not if you try to sing all these intervals as nicely as possible, since
You have gone up one syntonic comma! So, this sequence of notes is called a comma pump. In the 1500s the scientist Giovanni Battista Benedetti composed a piece of music to illustrate this effect. Adam Neely explains it here:
and here’s its carried out to excruciating excess:
It’s a wretchedly unpleasant thing, at least to my ears.
Azimuth 
Sounds fine to me. I guess a lifetime of listening to flanged guitars and various beep-boopy music has acclimated me to such things?
Sure, it could be a “cool effect” in the right context. So could the sound of breaking glass. But if I hit a piano key and it sounded like that, it would mean that one or more of the three strings was seriously out of tune, and I’d consider it unplayable.
As I’m sure John knows, “Our ears love these simple fractions” is a vast oversimplification, for at least two reasons:
1) As Blake pointed out, what sounds “good” depends on your personal and cultural experience, as well as mathematics. “Dissonant” notes are not necessarily unpleasant, any more than bitter flavors are.
2) Our ears (and brain) do not actually recognize simple fractions, they recognize when the overtones from two notes line up. Nylon and gut strings, most wind instruments, and some others produce overtones with simple fraction ratios, so music with simple fraction ratios sounds good on them. Percussion instruments, unless they’ve been very carefully tuned, don’t produce simple fraction overtones, which is why Indonesian gamelan music is not strongly based around simple fractions. In fact, the stiffness of piano wire causes it to deviation from simple fractions, especially in the highest and lowest registers, and so pianos tend to be tuned with “stretched” intervals.
Sorry about the long answer; I’m working on a book in which (2) is a central theme! Until it’s done, I’d recommend looking at David Benson’s book: https://homepages.abdn.ac.uk/d.j.benson/pages/html/music.pdf
Wow ! (alas, I’m too lousy a musician with too lousy an ear to say more.)
I once attended a concert of music performed with just intonation. As I recall, it was billed as non-Bachian music, in ironic tribute to Bach’s Well-Tempered Clavier. The organizers had a mathematical bent. One of them explained that the commas are a discrete analog of holonomies. So you could say this is music with curvature.
If commas are really a discrete analogue of holonomies then I, as a supposed expert on gauge theory and its discrete analogues (like spin networks and lattice gauge theory), should be able to make that precise!
So that’s an interesting gauntlet you just threw down there!
Since the Pythagorean comma is simpler I could start with that. Think of the circle of fifths
as a graph with 12 nodes and 12 edges. As we move along each edge, suppose the frequency goes up by a factor of 3/2. The issue is that when we go all the way around we are not ‘back where we started’.
So, we want to assign some group element to each oriented edge of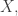
which records the fact that the frequency gets multiplied by 3/2 as we move along that edge.
For this we need to think about frequency ratios modulo octaves. We can do it as follows: take the multiplicative group of positive reals
and mod out by 2, getting the group
Note that we’re modding out by 2 multiplicatively, not additively as is more often done! So
is the group of frequency ratios mod octaves, and it’s isomorphic to the circle group, often called 
by physicists.
To put a
-connection on the graph 
means that we assign an element of 
to each oriented edge of 
We take all these elements to be ![[3/2] \in G.](https://s0.wp.com/latex.php?latex=%5B3%2F2%5D+%5Cin+G.&bg=ffffff&fg=333333&s=0&c=20201002)
This says mathematically that each time we move up a fifth on the circle of fifths, the frequency gets multiplied by 3/2, but we only care about frequencies mod octaves.
The holonomy as we go all the way around the circle of fifths is defined to be the product of the group elements labeling all the edges. This is
and this is not the identity, though it’s close: this is the Pythagorean comma. You can see it in this diagram made by AugPi:
Hey, neat explanation! And cool diagram!
I’ve long wondered about the simplicity of Lissajous patterns of those same melodic ratios compared to other ratios. For instance, 1:2 is just a bowtie shape, and 3/2 doesn’t have much more to it. It isn’t just our ear, there is a “clean elegance” to some ratios versus increasing business in others.