This is the last of the old series of This Week’s Finds. Soon the new series will start, focused on technology and environmental issues — but still with a hefty helping of math, physics, and other science.
When I decided to do something useful for a change, I realized that the best way to start was by interviewing people who take the future and its challenges seriously, but think about it in very different ways. So far, I’ve done interviews with:
• Tim Palmer on climate modeling and predictability.
• Thomas Fischbacher on sustainability and permaculture.
• Eliezer Yudkowsky on artificial intelligence and the art of rationality.
I hope to do more. I think it’ll be fun having This Week’s Finds be a dialogue instead of a monologue now and then.
Other things are changing too. I started a new blog! If you’re interested in how scientists can help save the planet, I hope you visit:
1) Azimuth, https://johncarlosbaez.wordpress.com
This is where you can find This Week’s Finds, starting now
Also, instead of teaching math in hot dry Riverside, I’m now doing research at the Centre for Quantum Technologies in hot and steamy Singapore. This too will be reflected in the new This Week’s Finds.
But now… the grand finale of This Week’s Finds in Mathematical Physics!
I’d like to take everything I’ve been discussing so far and wrap it up in a nice neat package. Unfortunately that’s impossible – there are too many loose ends. But I’ll do my best: I’ll tell you how to categorify the Riemann zeta function. This will give us a chance to visit lots of our old friends one last time: the number 24, string theory, zeta functions, torsors, Joyal’s theory of species, groupoidification, and more.
Let me start by telling you how to count.
I’ll assume you already know how to count elements of a set, and move right along to counting objects in a groupoid.
A groupoid is a gadget with a bunch of objects and a bunch of isomorphisms between them. Unlike an element of a set, an object of a groupoid may have symmetries: that is, isomorphisms between it and itself. And unlike an element of a set, an object of a groupoid doesn’t always count as “1 thing”: when it has n symmetries, it counts as “1/nth of a thing”. That may seem strange, but it’s really right. We also need to make sure not to count isomorphic objects as different.
So, to count the objects in our groupoid, we go through it, take one representative of each isomorphism class, and add 1/n to our count when this representative has n symmetries.
Let’s see how this works. Let’s start by counting all the n-element sets!
Now, you may have thought there were infinitely many sets with n elements, and that’s true. But remember: we’re not counting the set of n-element sets – that’s way too big. So big, in fact, that people call it a “class” rather than a set! Instead, we’re counting the groupoid of n-element sets: the groupoid with n-element sets as objects, and one-to-one and onto functions between these as isomorphisms.
All n-element sets are isomorphic, so we only need to look at one. It has n! symmetries: all the permutations of n elements. So, the answer is 1/n!.
That may seem weird, but remember: in math, you get to make up the rules of the game. The only requirements are that the game be consistent and profoundly fun – so profoundly fun, in fact, that it seems insulting to call it a mere “game”.
Now let’s be more ambitious: let’s count all the finite sets. In other words, let’s work out the cardinality of the groupoid where the objects are all the finite sets, and the isomorphisms are all the one-to-one and onto functions between these.
There’s only one 0-element set, and it has 0! symmetries, so it counts for 1/0!. There are tons of 1-element sets, but they’re all isomorphic, and they each have 1! symmetries, so they count for 1/1!. Similarly the 2-element sets count for 1/2!, and so on. So the total count is
1/0! + 1/1! + 1/2! + … = e
The base of the natural logarithm is the number of finite sets! You learn something new every day.
Spurred on by our success, you might want to find a groupoid whose cardinality is π. It’s not hard to do: you can just find a groupoid whose cardinality is 3, and a groupoid whose cardinality is .1, and a groupoid whose cardinality is .04, and so on, and lump them all together to get a groupoid whose cardinality is 3.14… But this is a silly solution: it doesn’t shed any light on the nature of π.
I don’t want to go into it in detail now, but the previous problem really does shed light on the nature of e: it explains why this number is related to combinatorics, and it gives a purely combinatorial proof that the derivative of ex is ex, and lots more. Try these books to see what I mean:
2) Herbert Wilf, Generatingfunctionology, Academic Press, Boston, 1994. Available for free at http://www.cis.upenn.edu/~wilf/.
3) F. Bergeron, G. Labelle, and P. Leroux, Combinatorial Species and Tree-Like Structures, Cambridge, Cambridge U. Press, 1998.
For example: if you take a huge finite set, and randomly pick a permutation of it, the chance every element is mapped to a different element is close to 1/e. It approaches 1/e in the limit where the set gets larger and larger. That’s well-known – but the neat part is how it’s related to the cardinality of the groupoid of finite sets.
Anyway, I have not succeeded in finding a really illuminating groupoid whose cardinality is π, but recently James Dolan found a nice one whose cardinality is π2/6, and I want to lead up to that.
Here’s a not-so-nice groupoid whose cardinality is π2/6. You can build a groupoid as the “disjoint union” of a collection of groups. How? Well, you can think of a group as a groupoid with one object: just one object having that group of symmetries. And you can build more complicated groupoids as disjoint unions of groupoids with one object. So, if you give me a collection of groups, I can take their disjoint union and get a groupoid.
So give me this collection of groups:
Z/1×Z/1, Z/2×Z/2, Z/3×Z/3, …
where Z/n is the integers mod n, also called the “cyclic group” with n elements. Then I’ll take their disjoint union and get a groupoid, and the cardinality of this groupoid is
1/12 + 1/22 + 1/32 + … = π2/6
This is not as silly as the trick I used to get a groupoid whose cardinality is π, but it’s still not perfectly satisfying, because I haven’t given you a groupoid of “interesting mathematical gadgets and isomorphisms between them”, as I did for e. Later we’ll see Jim’s better answer.
We might also try taking various groupoids of interesting mathematical gadgets and computing their cardinality. For example, how about the groupoid of all finite groups? I think that’s infinite – there are just “too many”. How about the groupoid of all finite abelian groups? I’m not sure, that could be infinite too.
But suppose we restrict ourselves to abelian groups whose size is some power of a fixed prime p? Then we’re in business! The answer isn’t a famous number like π, but it was computed by Philip Hall here:
4) Philip Hall, A partition formula connected with Abelian groups, Comment. Math. Helv. 11 (1938), 126-129.
We can write the answer using an infinite product:
1/(1-p-1)(1-p-2)(1-p-3) …
Or, we can write the answer using an infinite sum:
p(0)/p0 + p(1)/p1 + p(2)/p2 + …
Here p(n) is the number of “partitions” of n: that is, the number of ways to write it as a sum of positive integers in decreasing order. For example, p(4) = 5 since we can write 4 as a sum in 5 ways like this:
4 = 4
4 = 3+1
4 = 2+2
4 = 2+1+1
4 = 1+1+1+1
If you haven’t thought about this before, you can have fun proving that the infinite product equals the infinite sum. It’s a cute fact, and quite famous.
But Hall proved something even cuter. This number
p(0)/p0 + p(1)/p1 + p(2)/p2 + …
is also the cardinality of another, really different groupoid. Remember how I said you can build a groupoid as the “disjoint union” of a collection of groups? To get this other groupoid, we take the disjoint union of all the abelian groups whose size is a power of p.
Hall didn’t know about groupoid cardinality, so here’s how he said it:
The sum of the reciprocals of the orders of all the Abelian groups of order a power of p is equal to the sum of the reciprocals of the orders of their groups of automorphisms.
It’s pretty easy to see that sum of the reciprocals of the orders of all the Abelian groups of order a power of p is
p(0)/p0 + p(1)/p1 + p(2)/p2 + …
To do this, you just need to show that there are p(n) abelian groups with pn elements. If I shows you how it works for n = 4, you can guess how the proof works in general:
4 = 4 Z/p4
4 = 3+1 Z/p3 × Z/p
4 = 2+2 Z/p2 × Z/p2
4 = 2+1+1 Z/p2 × Z/p2 × Z/p
4 = 1+1+1+1 Z/p × Z/p × Z/p × Z/p
So, the hard part is showing that
p(0)/p0 + p(1)/p1 + p(2)/p2 + …
is also the sum of the reciprocals of the sizes of the automorphism groups of all groups whose size is a power of p.
I learned of Hall’s result from Aviv Censor, a colleague who is an expert on groupoids. He had instantly realized this result had a nice formulation in terms of groupoid cardinality. We went through several proofs, but we haven’t yet been able to extract any deep inner meaning from them:
5) Avinoam Mann, Philip Hall’s “rather curious” formula for abelian p-groups, Israel J. Math. 96 (1996), part B, 445-448.
6) Francis Clarke, Counting abelian group structures, Proceedings of the AMS, 134 (2006), 2795-2799.
However, I still have hopes, in part because the math is related to zeta functions… and that’s what I want to turn to now.
Let’s do another example: what’s the cardinality of the groupoid of semisimple commutative rings with n elements?
What’s a semisimple commutative ring? Well, since we’re only talking about finite ones, I can avoid giving the general definition and take advantage of a classification theorem. Finite semisimple commutative rings are the same as finite products of finite fields. There’s a finite field with pn whenever p is prime and n is a positive integer. This field is called Fpn, and it has n symmetries. And that’s all the finite fields! In other words, they’re all isomorphic to these.
This is enough to work out the cardinality of the groupoid of semisimple commutative rings with n elements. Let’s do some examples. Let’s try n = 6, for example.
This one is pretty easy. The only way to get a finite product of finite fields with 6 elements is to take the product of F2 and F3:
F2 × F3
This has just one symmetry – the identity – since that’s all the symmetries either factor has, and there’s no symmetry that interchanges the two factors. (Hmm… you may need check this, but it’s not hard.)
Since we have one object with one symmetry, the groupoid cardinality is
1/1 = 1
Let’s try a more interesting one, say n = 4. Now there are two options:
F4
F2 × F2
The first option has 2 symmetries: remember, Fpn has n symmetries. The second option also has 2 symmetries, namely the identity and the symmetry that switches the two factors. So, the groupoid cardinality is
1/2 + 1/2 = 1
But now let’s try something even more interesting, like n = 16. Now there are 5 options:
F16
F8×F2
F4×F4
F4×F2×F2
F2×F2×F2×F2
The field F16 has 4 symmetries because 16 = 24, and any field Fpn has n symmetries. F8×F2 has 3 symmetries, coming from the symmetries of the first factor. F4×F4 has 2 symmetries in each factor and 2 coming from permutations of the factors, for a total of 2× 2×2 = 8. F4×F2×F2 has 2 symmetries coming from those of the first factor, and 2 symmetries coming from permutations of the last two factors, for a total of 2×2 = 4 symmetries. And finally, F2×F2×F2×F2 has 24 symmetries coming from permutations of the factors. So, the cardinality of this groupoid works out to be
1/4 + 1/3 + 1/8 + 1/4 + 1/24
Hmm, let’s put that on a common denominator:
6/24 + 8/24 + 3/24 + 6/24 + 1/24 = 24/24 = 1
So, we’re getting the same answer again: 1.
Is this just a weird coincidence? No: this is what we always get! For any positive integer n, the groupoid of n-element semsimple commutative rings has cardinality 1. For a proof, see:
7) John Baez and James Dolan, Zeta functions, at http://ncatlab.org/johnbaez/show/Zeta+functions
Now, you might think this fact is just a curiosity, but actually it’s a step towards categorifying the Riemann zeta function. The Riemann zeta function is
ζ(s) = ∑n > 0 n-s
It’s an example of a “Dirichlet series”, meaning a series of this form:
∑n > 0 an n-s
In fact, any reasonable way of equipping finite sets with extra stuff gives a Dirichlet series – and if this extra stuff is “being a semisimple commutative ring”, we get the Riemann zeta function.
To explain this, I need to remind you about “stuff types”, and then explain how they give Dirichlet series.
A stuff type is a groupoid Z where the objects are finite sets equipped with “extra stuff” of some type. More precisely, it’s a groupoid with a functor to the groupoid of finite sets. For example, Z could be the groupoid of finite semsimple commutative rings – that’s the example we care about now. Here the functor forgets that we have a semisimple commutative ring, and only remembers the underlying finite set. In other words, it forgets the “extra stuff”.
In this example, the extra stuff is really just extra structure, namely the structure of being a semisimple commutative ring. But we could also take X to be the groupoid of pairs of finite sets. A pair of finite sets is a finite set equipped with honest-to-goodness extra stuff, namely another finite set!
Structure is a special case of stuff. If you’re not clear on the difference, try this:
8) John Baez and Mike Shulman, Lectures on n-categories and cohomology, Sec. 2.4: Stuff, structure and properties, in n-Categories: Foundations and Applications, eds. John Baez and Peter May, Springer, Berlin, 2009. Also available as arXiv:math/0608420.
Then you can tell your colleagues: “I finally understand stuff.” And they’ll ask: “What stuff?” And you can answer, rolling your eyes condescendingly: “Not any particular stuff – just stuff, in general!”
But it’s not really necessary to understand stuff in general here. Just think of a stuff type as a groupoid where the objects are finite sets equipped with extra bells and whistles of some particular sort.
Now, if we have a stuff type, say Z, we get a list of groupoids Z(n). How? Simple! Objects of Z are finite sets equipped with some particular type of extra stuff. So, we can take the objects of Z(n) to be the n-element sets equipped with that type of extra stuff. The groupoid Z will be a disjoint union of these groupoids Z(n).
We can encode the cardinalities of all these groupoids into a Dirichlet series:
z(s) = ∑n > 0 |Z(n)| n-s
where |Z(n)| is the cardinality of Z(n). In case you’re wondering about the minus sign: it’s just a dumb convention, but I’m too overawed by the authority of tradition to dream of questioning it, even though it makes everything to come vastly more ugly.
Anyway: the point is that a Dirichlet series is like the “cardinality” of a stuff type. To show off, we say stuff types categorify Dirichlet series: they contain more information, and they’re objects in a category (or something even better, like a 2-category) rather than elements of a set.
Let’s look at an example. When Z is the groupoid of finite semisimple commutative rings, then
|Z(n)| = 1
so the corresponding Dirichlet series is the Riemann zeta function:
z(s) = ζ(s)
So, we’ve categorified the Riemann zeta function! Using this, we can construct an interesting groupoid whose cardinality is
ζ(2) = ∑n > 0 n-2 = π2/6
How? Well, let’s step back and consider a more general problem. Any stuff type Z gives a Dirichlet series
z(s) = ∑n > 0 |Z(n)| n-s
How can use this to concoct a groupoid whose cardinality is z(s) for some particular value of s? It’s easy when s is a negative integer (here that minus sign raises its ugly head). Suppose S is a set with s elements:
|S| = s
Then we can define a groupoid as follows:
Z(-S) = ∑n > 0 Z(n) × nS
Here we are playing some notational tricks: nS means “the set of functions from S to our favorite n-element set”, the symbol × stands for the product of groupoids, and ∑ stands for what I’ve been calling the “disjoint union” of groupoids (known more technically as the “coproduct”). So, Z(-S) is a groupoid. But this formula is supposed to remind us of a simpler one, namely
z(-s) = ∑n > 0 |Z(n)| ns
and indeed it’s a categorified version of this simpler formula.
In particular, if we take the cardinality of the groupoid Z(-S), we get the number z(-s). To see this, you just need to check each step in this calculation:
|Z(-S)| = |∑ Z(n) × nS|
= ∑ |Z(n) × nS|
= ∑ |Z(n)| × |nS|
= ∑ |Z(n)| × ns
= z(-s)
The notation is supposed to make these steps seem plausible.
Even better, the groupoid Z(-S) has a nice description in plain English: it’s the groupoid of finite sets equipped with Z-stuff and a map from the set S.
Well, okay – I’m afraid that’s what passes for plain English among mathematicians! We don’t talk to ordinary people very often. But the idea is really simple. Z is some sort of stuff that we can put on a finite set. So, we can do that and also choose a map from S to that set. And there’s a groupoid of finite sets equipped with all this extra baggage, and isomorphisms between those.
If this sounds too abstract, let’s do an example. Say our favorite example, where Z is the groupoid of finite semisimple commutative rings. Then Z(-S) is the groupoid of finite semisimple commutative rings equipped with a map from the set S.
If this still sounds too abstract, let’s do an example. Do I sound repetitious? Well, you see, category theory is the subject where you need examples to explain your examples – and n-category theory is the subject where this process needs to be repeated n times. So, suppose S is a 1-element set – we can just write
S = 1
Then Z(-1) is a groupoid where the objects are finite semisimple commutative rings with a chosen element. The isomorphisms are ring isomorphisms that preserve the chosen element. And the cardinality of this groupoid is
|Z(-1)| = ζ(-1) = 1 + 2 + 3 + …
Whoops – it diverges! Luckily, people who study the Riemann zeta function know that
1 + 2 + 3 + … = -1/12
They get this crazy answer by analytically continuing the Riemann zeta function ζ(s) from values of s with a big positive real part, where it converges, over to values where it doesn’t. And it turns out that this trick is very important in physics. In fact, back in "week124" – "week126", I explained how this formula
ζ(-1) = -1/12
is the reason bosonic string theory works best when our string has 24 extra dimensions to wiggle around in besides the 2 dimensions of the string worldsheet itself.
So, if we’re willing to allow this analytic continuation trick, we can say that
Someday people will see exactly how this is related to bosonic string theory. Indeed, it should be just a tiny part of a big story connecting number theory to string theory… some of which is explained here:
9) J. M. Luck, P. Moussa, and M. Waldschmidt, eds., Number Theory and Physics, Springer Proceedings in Physics, Vol. 47, Springer-Verlag, Berlin, 1990.
10) C. Itzykson, J. M. Luck, P. Moussa, and M. Waldschmidt, eds, From Number Theory to Physics, Springer, Berlin, 1992.
Indeed, as you’ll see in these books (or in "week126"), the function we saw earlier:
1/(1-p-1)(1-p-2)(1-p-3) … = p(0)/p0 + p(1)/p1 + p(2)/p2 + …
is also important in string theory: it shows up as a “partition function”, in the physical sense, where the number p(n) counts the number of ways a string can have energy n if it has one extra dimension to wiggle around in besides the 2 dimensions of its worldsheet.
But it’s the 24th power of this function that really matters in string theory – because bosonic string theory works best when our string has 24 extra dimensions to wiggle around in. For more details, try:
11) John Baez, My favorite numbers: 24. Available at http://math.ucr.edu/home/baez/numbers/24.pdf
But suppose we don’t want to mess with divergent sums: suppose we want a groupoid whose cardinality is, say,
ζ(2) = 1-2 + 2-2 + 3-2 + … = π2/6
Then we need to categorify the evalution of Dirichlet series at positive integers. We can only do this for certain stuff types – for example, our favorite one. So, let Z be the groupoid of finite semisimple commutative rings, and let S be a finite set. How can we make sense of
Z(S) = ∑n > 0 Z(n) × n-S ?
The hard part is n-S, because this has a minus sign in it. How can we raise an n-element set to the -Sth power? If we could figure out some sort of groupoid that serves as the reciprocal of an n-element set, we’d be done, because then we could take that to the Sth power. Remember, S is a finite set, so to raise something (even a groupoid) to the Sth power, we just multiply a bunch of copies of that something – one copy for each element of S.
So: what’s the reciprocal of an n-element set? There’s no answer in general – but there’s a nice answer when that set is a group, because then that group gives a groupoid with one object, and the cardinality of this groupoid is just 1/n.
Here is where our particular stuff type Z comes to the rescue. Each object of Z(n) is a semisimple commutative ring with n elements, so it has an underlying additive group – which is a group with n elements!
So, we don’t interpret Z(n) × n-S as an ordinary product, but something a bit sneakier, a “twisted product”. An object in Z(n) × n-S is just an object of Z(n), that is an n-element semisimple commutative ring. But we define a symmetry of such an object to be a symmetry of this ring together with an S-tuple of elements of its underlying additive group. We compose these symmetries with the help of addition in this group. This ensures that
|Z(n) × n-S| = |Z(n)| × n-s
when |S| = s. And this in turn means that
|Z(S)| = |∑ Z(n) × n-S|
= ∑ |Z(n) × n-S|
= ∑ |Z(n)| × n-s
= ζ(-s)
So, in particular, if S is a 2-element set, we can write
S = 2
for short and get
|Z(2)| = ζ(2) = π2/6
Can we describe the groupoid Z(2) in simple English, suitable for a nice bumper sticker? It’s a bit tricky. One reason is that I haven’t described the objects of Z(2) as mathematical gadgets of an appealing sort, as I did for Z(-1). Another closely related reason is that I only described the symmetries of any object in Z(2) – or more technically, morphisms from that object to itself. It’s much better if we also describe morphisms from one object to another.
For this, it’s best to define Z(n) × n-S with the help of torsors. The idea of a torsor is that you can take the one-object groupoid associated to any group G and find a different groupoid, which is nonetheless equivalent, and which is a groupoid of appealing mathematical gadgets. These gadgets are called “G-torsors”. A “G-torsor” is just a nonempty set on which G acts freely and transitively:
12) John Baez, Torsors made easy, http://math.ucr.edu/home/baez/torsors.html
All G-torsors are isomorphic, and the group of symmetries of any G-torsor is G.
Now, any ring R has an underlying additive group, which I will simply call R. So, the concept of “R-torsor” makes sense. This lets us define an object of Z(n) × n-S to be an n-element semisimple commutative ring R together with an S-tuple of R-torsors.
But what about the morphisms between these? We define a morphism between these to be a ring isomorphism together with an S-tuple of torsor isomorphisms. There’s a trick hiding here: a ring isomorphism f: R → R’ lets us take any R-torsor and turn it into an R’-torsor, or vice versa. So, it lets us talk about an isomorphism from an R-torsor to an R’-torsor – a concept that at first might have seemed nonsensical.
Anyway, it’s easy to check that this definition is compatible with our earlier one. So, we see:
I did a silly change of variables here: I thought this bumper sticker would sell better if I said “n-tuple” instead of “S-tuple”. Here n is any positive integer.
While we’re selling bumper stickers, we might as well include this one:
Now, you might think this fact is just a curiosity. But I don’t think so: it’s actually a step towards categorifying the general theory of zeta functions. You see, the Riemann zeta function is just one of many zeta functions. As Hasse and Weil discovered, every sufficiently nice commutative ring R has a zeta function. The Riemann zeta function is just the simplest example: the one where R is the ring of integers. And the cool part is that all these zeta functions come from stuff types using the recipe I described!
How does this work? Well, from any commutative ring R, we can build a stuff type ZR as follows: an object of ZR is a finite semisimple commutative ring together with a homomorphism from R to that ring. Then it turns out the Dirichlet series of this stuff type, say
ζR(s) = ∑n > 0 |ZR(n)| n-s
is the usual Hasse-Weil zeta function of the ring R!
Of course, that fact is vastly more interesting if you already know and love Hasse-Weil zeta functions. You can find a definition of them either in my paper with Jim, or here:
12) Jean-Pierre Serre, Zeta and L functions, Arithmetical Algebraic Geometry (Proc. Conf. Purdue Univ., 1963), Harper and Row, 1965, pp. 82–92.
But the basic idea is simple. You can think of any commutative ring R as the functions on some space – a funny sort of space called an “affine scheme”. You’re probably used to spaces where all the points look alike – just little black dots. But the points of an affine scheme come in many different colors: for starters, one color for each prime power pk! The Hasse-Weil zeta function of R is a clever trick for encoding the information about the numbers of points of these different colors in a single function.
Why do we get points of different colors? I explained this back in "week205". The idea is that for any commutative ring k, we can look at the homomorphisms
f: R → k
and these are called the “k-points” of our affine scheme. In particular, we can take k to be a finite field, say Fpn. So, we get a set of points for each prime power pn. The Hasse-Weil zeta function is a trick for keeping track of many Fpn-points there are for each prime power pn.
Given all this, you shouldn’t be surprised that we can get the Hasse-Weil zeta function of R by taking the Dirichlet series of the stuff type ZR, where an object is a finite semisimple commutative ring k together with a homomorphism f: R → k. Especially if you remember that finite semisimple commutative rings are built from finite fields!
In fact, this whole theory of Hasse-Weil zeta functions works for gadgets much more general than commutative rings, also known as affine schemes. They can be defined for “schemes of finite type over the integers”, and that’s how Serre and other algebraic geometers usually do it. But Jim and I do it even more generally, in a way that doesn’t require any expertise in algebraic geometry. Which is good, because we don’t have any.
I won’t explain that here – it’s in our paper.
I’ll wrap up by making one more connection explicit – it’s sort of lurking in what I’ve said, but maybe it’s not quite obvious.
First of all, this idea of getting Dirichlet series from stuff types is part of the groupoidification program. Stuff types are a generalization of “structure types”, often called “species”. André Joyal developed the theory of species and showed how any species gives rise to a formal power series called its generating function. I told you about this back in "week185" and "week190". The recipe gets even simpler when we go up to stuff types: the generating function of a stuff type Z is just
∑n ≥ 0 |Z(n)| zn
Since we can also describe states of the quantum harmonic oscillator as power series, with zn corresponding to the nth energy level, this
lets us view stuff types as states of a categorified quantum harmonic oscillator! This explains the combinatorics of Feynman diagrams:
14) Jeffrey Morton, Categorified algebra and quantum mechanics, TAC 16 (2006), 785-854, available at http://www.emis.de/journals/TAC/volumes/16/29/16-29abs.html Also available as arXiv:math/0601458.
And, it’s a nice test case of the groupoidification program, where we categorify lots of algebra by saying “wherever we see a number, let’s try to think of it as the cardinality of a groupoid”:
15) John Baez, Alex Hoffnung and Christopher Walker, Higher-dimensional algebra VII: Groupoidification, available as arXiv:0908.4305
But now I’m telling you something new! I’m saying that any stuff type also gives a Dirichlet series, namely
∑n > 0 |Z(n)| n-s
This should make you wonder what’s going on. My paper with Jim explains it – at least for structure types. The point is that the groupoid of finite sets has two monoidal structures: + and ×. This gives the category of structure types two monoidal structures, using a trick called “Day convolution”. The first of these categorifies the usual product of formal power series, while the second categorifies the usual product of Dirichlet series. People in combinatorics love the first one, since they love chopping a set into two disjoint pieces and putting a structure on each piece. People in number theory secretly love the second one, without fully realizing it, because they love taking a number and decomposing it into prime factors. But they both fit into a single picture!
There’s a lot more to say about this, because actually the category of structure types has five monoidal structures, all fitting together in a nice way. You can read a bit about this here:
16) nLab, Schur functors, http://ncatlab.org/nlab/show/Schur+functor
This is something Todd Trimble and I are writing, which will eventually evolve into an actual paper. We consider structure types for which there is a vector space of structures for each finite set instead of a set of structures. But much of the abstract theory is similar. In particular, there are still five monoidal structures.
Someday soon, I hope to show that two of the monoidal structures on the category of species make it into a “ring category”, while the other two – the ones I told you about, in fact! – are better thought of as “comonoidal” structures, making it into a “coring category”. Putting these together, the category of species should become a “biring category”. Then the fifth monoidal structure, called “plethysm”, should make it into a monoid in the monoidal bicategory of biring categories!
This sounds far-out, but it’s all been worked out at a decategorified level: rings, corings, birings, and monoids in the category of birings:
17) D. Tall and Gavin Wraith, Representable functors and operations on rings, Proc. London Math. Soc. (3), 1970, 619-643.
18) James Borger and B. Wieland, Plethystic algebra, Advances in Mathematics 194 (2005), 246-283. Also available at http://wwwmaths.anu.edu.au/~borger/papers/03/paper03.html
19) Andrew Stacey and S. Whitehouse, The hunting of the Hopf ring, Homology, Homotopy and Applications, 11 (2009), 75-132, available at http://intlpress.com/HHA/v11/n2/a6/ Also available as arXiv:0711.3722.
Borger and Wieland call a monoid in the category of birings a “plethory”. The star example is the algebra of symmetric functions. But this is basically just a decategorified version of the category of Vect-valued species. So, the whole story should categorify.
In short: starting from very simple ideas, we can very quickly find a treasure trove of rich structures. Indeed, these structures are already staring us in the face – we just need to open our eyes. They clarify and unify a lot of seemingly esoteric and disconnected things that mathematicians and physicists love.
I think we are just beginning to glimpse the real beauty of math and physics. I bet it will be both simpler and more startling than most people expect.
I would love to spend the rest of my life chasing glimpses of this beauty. I wish we lived in a world where everyone had enough of the bare necessities of life to do the same if they wanted – or at least a world that was safely heading in that direction, a world where politicians were looking ahead and tackling problems before they became desperately serious, a world where the oceans weren’t dying.
But we don’t.
Certainty of death. Small chance of success. What are we waiting for? – Gimli


The answer isn’t a famous number like π, but it was computed by Philip Hall here:
This is called the “partition function”. (Joke due to Matt Szczesny.)
After getting your comment about this, I put this joke in “week300”, in a somewhat implicit way – but I didn’t credit Matt since I thought Jim Dolan invented it. I guess great minds think alike.
Wiping a tear from my eye (I think I began tuning in to TWF in around 1997).
This paper explains how a finitely abelian group is a product of such things of order a prime to a power, and that the order of is the product of the order of
is the product of the order of  for these factors.
for these factors.
Theorem 4.1 then gives an expression for . So maybe someone clever could do the sum.
. So maybe someone clever could do the sum.
Hmm, so isn’t the cardinality we want the product over either of
either of
a) The sum of the reciprocals of the orders of all the Abelian groups of order a power of ,
,
or equivalently of
b) The sum of the reciprocals of the orders of their groups of automorphisms?
David wrote:
That’s right. A bit more explicitly, it’s the product over primes
where
I was leaving it as a kind of puzzle to determine whether this converges, and if so, what to. Interesting that the philosopher in the crowd was the first to tackle this…
(It may or may not help to know a bit about the Euler function, since is the reciprocal of the Euler function evaluated at
is the reciprocal of the Euler function evaluated at  .)
.)
I had some fun writing a little program to sum this up numerically – this was a nice exercise with Python generator objects. The partial sum after 7000000 terms (ordered by size of group), is about 33.172. Once it exceeded 24 I lost hope of it converging ;-)
And then I saw a simple reason it is divergent – if you just consider groups of order p for p prime, each of these has automorphism group of order p-1, and, termwise,
where the right-hand series diverges. (Unless we play some crazy re-summation tricks!)
I also just wanted to add to what everyone else is saying about what a great column TWF has been: I have learned so much and gotten a lot of enjoyment from following it. Thank you, and best wishes for success (we need it!) in your new endeavors.
Thanks very much, Charles! I’m glad you enjoyed TWF… and I hope you still do next week.
Yes, the cardinality diverges. Your proof is better, but one can also notice that
and so the infinite product
diverges because the infinite sum
diverges. But this is really just a roundabout way of saying what you’re saying: the cyclic groups of order give the ‘leading order contribution’ to the cardinality of the groupoid of finite abelian groups, and this already diverges.
give the ‘leading order contribution’ to the cardinality of the groupoid of finite abelian groups, and this already diverges.
(By the way, to get LaTeX to work here, you need to write
something like
$latex 24^2 = 576 $
with the word ‘latex’ appearing directly after the first dollar sign – no space. I fixed your comment.)
The funny-cardinality of the cyclic groups of prime order is infinite, as several people have now proved. Or, to put it another way, the funny-cardinality of the finite abelian simple groups is infinite. What is the funny-cardinality of the finite NON-abelian simple groups?
Every finite non-abelian simple group S has |S| inner automorphisms, and if I recall correctly, |Aut(S)| is either |S| or 2|S| for all (or nearly all?) such S. I think the answer here might be finite. Does anyone know? Should anyone care?
Maybe we should care… but this recent comment by Richard Borcherds on the thread Theo pointed us to suggests that maybe the answer is doomed to be infinite — unless most groups of order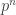 are abelian when
are abelian when 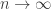 , which sounds unlikely to me.
, which sounds unlikely to me.
I know there are loads of groups of p-power order, but none of them are non-abelian simple.
Oh, simple! I didn’t see that word. I thought you were just asking about finite nonabelian groups.
Hmm, I’ll wildly guess that the groupoid of finite simple nonabelian groups does have finite cardinality.
David wrote:
Sorry, this one was a real tear-jerker. I promise that future issues won’t be so maudlin!
Cool! That’s 13 years, 52 weeks a year… you must have read about 676 issues!
I’m sure glad you tuned in: you’ve done a huge amount to spread the word about n-categories.
Looking back, it’s quite remarkable how much attitudes have changed toward these structures. I remember Noam Elkies, back in 1997, complaining that I went beyond chutzpah into parochialism when I put two problems involving n-categories on a list of ‘neo-Hilbert problems’ for the 20th century — the stabilization hypothesis and tangle hypothesis. Lurie has now proved the first one, and partially proved the second. He’s now at Harvard along with Elkies. I can’t tell whether this means I was on the right track or not. Were they solved so quickly because they were too easy to be interesting, or because Lurie is so smart?
It’s also interesting that Elkies put this problem on his list:
I replied saying that this sounded great, but that I hadn’t realized the Langlands program had been ‘subsumed’. He said it had… but I guess I still don’t understand what he meant.
Does anyone know?
I finally made it in a TWF! Just in time.
What a great run. Good luck with the new TWF.
Thanks!
Now I’m sorry I never got around to mentioning your work on ‘the field with one element’… though we did discuss it in the blog comments.
Luckily, I didn’t promise that I’d never talk about pure math in the new This Week’s Finds. (And if I decide the planet is doomed, I’ll return to pure math full time. )
)
I ought to remember, having biographized and Bibliographized Isaac Asimov, in Gale’s Encyclopedia of Computer Science, but I half-remember that his last science column in The Magazine of Fantasy & Science Fiction was #300.
Isaac Asimov Home Page
Welcome to the Isaac Asimov Home Page. Here you’ll find a comprehensive collection of resources pertaining to Isaac Asimov (1920-1992), the quintessential author, who in his lifetime wrote over 500 books that enlightened, entertained, and spanned the realm of human knowledge.
Home to Isaac Asimov’s monthly science column for over thirty-three years, The Magazine of Fantasy & Science Fiction, founded in 1949, is the award-winning SF magazine which is the original publisher of SF classics like Stephen King’s Dark Tower, Daniel Keyes’s “Flowers for Algernon” and Walter M. Miller’s A Canticle for Leibowitz
Jonathan wrote:
Really? That would be cool. Asimov was my childhood hero, and when I was 8, I sent him a type-written letter asking him what were the orbital radii of the moons of Jupiter. He sent me a type-written postcard congratulating me on my typing skill and politely telling me to look it up. I was mortified with embarrassment for years thereafter — what had I been thinking? Only recently have I become able to recall this incident without shame.
It was actually #399.
Damn, now I need to do 99 more.
Well that’s ten wonderful years of reading TWFiMP for me. On to the future with TWF!
Thanks! Will do!
(The link in #18 should end .html , rather than .htm .)
Thanks – fixed!
Also, there is some discussion on the cardinality of the groupoid of (abelian) groups at http://mathoverflow.net/questions/30459/counting-the-groups-of-order-n-weighted-by-1-autg
Sad that it ends, I had enjoyed it very much, esp. week186.
Thanks! That was indeed close to a local maximum — or maybe it occurred at week187. I hadn’t fully realized back then that I was doing a baby case of the theory of motives. The process of breaking up a flag variety, or partial flag variety, into a sum of Bruhat cells is the simplest case of decomposing a variety into motives, and the way this expresses the q-polynomial as a sum of powers of q is a baby case of how zeta functions work when you decompose a variety into motives. So indeed all the stuff Jim and I were learning then should fit nicely into what we’re doing now, namely categorifying these zeta functions. Jim has been thinking about motives a lot, too. If we make real progress I may write it up as further papers on the nLab, instead of using This Week’s Finds to explain it. Not sure. But there really is a nice big story waiting to be told in a simple way.
Week 186 was my favorite TWF also!
Apparently there is some current work with quantum cohomology on an old idea of extensions of motives, maybe somehow connectable to your and Jim’s thoughts?
Your link to Week 205 is broken (missing .html).
Fixed! Thanks.
[…] This Week's Finds in Mathematical Physics (Week 300) « Azimuth […]
Is there any proof that Riemann zeta function is the only function that can be used to obtain the value of ?
?
What if there exists some other function that gives different value of this sum ?
What cardinality would have “THE GROUPOID OF FINITE SEMISIMPLE COMMUTATIVE RINGS WITH A CHOSEN ELEMENT” in that situation ?
Mceier wrote:
No, there are infinitely many functions that can be used to obtain a value for , and you can find one that gives you any answer you want.
, and you can find one that gives you any answer you want.
This is why it’s so interesting that the zeta function gives the “right” value.
But the big question is: what do we mean by “right”?
First of all: throughout quantum field theory and string theory, people use zeta function regularization to extract finite answers from divergent sums, and these answers match the results of experiments! It would be nice to see precisely which values of divergent sums have been “experimentally confirmed”.
Secondly, these answers are “right” in that they fit into a beautifully consistent mathematical framework.
But I still consider this issue somewhat mysterious, and that’s one reason I’ve kept coming back to it in This Week’s Finds. See week126 for more on how to use zeta function regularization to obtain
and see a href = “http://math.ucr.edu/home/baez/week127.html”>week127 to learn the “right” value of
Another reason for coming back to these formulas again and again is the appeal of the forbidden – everyone who studies math has gone through a phase of being taught that it’s no good to think about these things.
For some more discussion of this, try the curiously titled article:
• E. Elizalde, Zeta-function regularization is uniquely defined and well
Also:
• An Huang, On twisted Virasoro operators and number theory.
which is infinitely more readable – at least in section 1 – than the title might suggest.
That’s interesting. Thank you for the answer :)
Thanks so much for all the information and inspiration!
I am glad that you decided to end with something related to structors (“combinatorial species”) and stuff types. If the planet can spare a few hours of your time during the next few years, I hope you &c. can develop all this further. Earlier this year, I started to think again about categorifying circuit theory, and was stunned when by chance I came across your posts on that, which were far beyond what I had come up with. I hope you will develop that line of thought further!
Hi! I know who you are! Great to “see” you again! Thanks for the comments!
I hope you look at my papers with James Dolan and Todd Trimble, because they go into a lot more detail that I was able to in “week300”, and I think you’re uniquely placed to enjoy them
I wasn’t really “categorifying” circuit theory — that refers to a quasi-systematic process of replacing sets by categories, functions by functors and equations by natural isomorphisms. I was applying category theory to understand electrical circuits and more general open systems. This is one activity I can easily justify continuing, since I have a job here at the Centre for Quantum Technologies, so I’d feel awkard devoting full time to environmental work… but they are interested in circuits of many kinds, especially quantum ones!
John,
Congratulations for 300 TWF and wish you a very best on the next chapter on your adventure. It’s been wonderful time to read all those wonderful essays. I learned so much and will learn from them for many years to come. Good luck and wish to see you again some time soon.
Demian
P.S. Do you plan to either publish or just collect 300 TWF into a single book or file? That wold be very helpful.
Hi, Demian! What are you up to, these days?
I don’t think publishing the existing This Week’s Finds in Mathematical Physics as a book would be very helpful — after all, a key component is the links. But you can download a copy of all 300 issues for free, here, and I urge everyone to do this. When civilization collapses, I want at least one hard drive containing my magnum opus to survive!
(If anyone is willing to inscribe it on stone tablets for a reasonable fee, please contact me by carrier pigeon.)
If I have time, I’d like to take certain themes that appear over and over in This Week’s Finds, and develop them into more coherent essays. I should start by writing about my favorite numbers… I actually owe the Glasgow Mathematical Journal a paper on that topic.
Thanks.
I have just finished downloading html version of TWF. For some reason, links for figures don’t work, even though all the jpg files seems to be included. It’s probably due to original links being in a different directory or something. I will fix them later when I need them.
I am currently a visiting faculty member at a small liberal art college called Kenyon College. (You may have just met my colleague Ben Schumacher at Cambridge.) I spend most of time thinking about neutron stars nowadays (dealing with reality for the first time in my career!), but still thinking about crazier stuff occasionally. Specifically, I am thinking about spending sometime learning about exotic structures despite the fact that I know the danger of spending full time on “crazy stuff”. I remember seeing Tevian Dray about 10 years ago at one of a small relativity meeting talking about Octonions (why? :-)), in front of largely skeptical audience. Probably, I was the only one at the meeting who were excited about his talk essentially because I had some knowledge from your TWF essays.
Let me know if you have chance to travel back to US for sometime next year. We really want to bring you as a colloquium speaker.
Cheers,
Demian
Demian wrote:
That’s strange. On my website almost all the jpg files are in the same directory as the issues of This Week’s Finds, so the pictures should work if you have all those files in the same directory.
If you figure out the problem, please let me know here. I would like to make this stuff work easily for everyone.
I realize now that I may occasionally be sloppy and include links to pictures in subdirectories, e.g. pictures of Platonic solids may be linked to my “dodecahedron” subdirectory. These links will break.
I would like to fix everything and make it nice…
Cool! I guess if you’re going to start dealing with reality late in life, it helps to start with something very abstract and distant, like neutron stars. Then later you can look at things here on Earth.
I’m glad you’re interested in exotic structures, though.
If I come to the US anytime soon I’ll try to remember to let you know! Right now I am very excited about the possibilities of exploring Asia. Laos, Thailand, Borneo…
I guess the categorification-skeptic might say “All very well this categorification of the Riemann zeta function for specific values, but what it does it tell us about the real purpose of the zeta function – its role in controlling the distribution of the primes? Where is your analytic continuation of THE GROUPOID OF FINITE SEMISIMPLE COMMUTATIVE RINGS EQUIPPED WITH AN -TUPLE OF TORSORS to complex
-TUPLE OF TORSORS to complex  ? What would it mean to say nontrivial zeros sit on the critical line? What is the categorification of the functional equation?”
? What would it mean to say nontrivial zeros sit on the critical line? What is the categorification of the functional equation?”
The categorification-skeptic wrote:
We’re working on it… slowly. One problem is figuring out how to categorify complex numbers. Of course Steve Schanuel and Robbie Gates and Tom Leinster and Marcelo Fiore have some nice ideas on that:
• Andreas Blass, Seven trees in one, Jour. Pure Appl. Alg. 103 (1995), 1-21. Also available at: http://www.math.lsa.umich.edu/~ablass/cat.html
• Robbie Gates, On the generic solution to P(X) = X in distributive categories, Jour. Pure Appl. Alg. 125 (1998), 191-212.
• Marcelo Fiore and Tom Leinster, An objective representation of the Gaussian integers, Jour. Symb. Comp. 37 (2004), 707-716. Also available as math/0211454.
• Marcelo Fiore and Tom Leinster, Objects of categories as complex numbers, Adv. Math. 190 (2005), 264-277. Also available as math/0212377.
• Marcelo Fiore, Isomorphisms of generic recursive polynomial types, to appear in 31st Symposium on Principles of Programming Languages (POPL04). Also available at http://www.cl.cam.ac.uk/~mpf23/papers/Types/recisos.ps.gz
But of course we need a way to categorify complex numbers that’s relevant to zeta functions… and for this, we need to ponder the relatives of the Riemann hypothesis that have been proved… like the Weil conjectures.
Indeed, the Riemann zeta function is probably the last zeta function that we’ll understand deeply. The more general Hasse-Weil zeta functions that Jim and I categorified include a lot of more tractable examples, like the ones that form the topic of the Weil conjectures. Instead of a cavalry charge into a brick wall, I much prefer a gentle approach where we gradually understand things better and better. The Weil conjectures are just like the Riemann hypothesis, except they’re known to be true for a comprehensible reason, while the Riemann hypothesis would only be true for a comprehensible reason if some dreams about the field of characteristic zero came to fruition.
And if you back away from the Riemann zeta function, and ponder the more general Hasse-Weil zeta functions, you’ll see it’s a bit unfair to say the “real purpose” of the zeta function is to control the distribution of primes — as if that’s all there was to it. You might equally say that the real purpose of zeta functions in arithmetic geometry is to count the k-points of a scheme for all finite fields k. And this viewpoint makes categorifying the zeta function a completely natural act, as my paper with Jim tries to show. Natural — and part of a big yet unexplored aspect of the theory of species: the multiplicative aspect!
So, there’s more to life than trying to prove the Riemann hypothesis.
At which point the scales fall from the eyes of the categorification-skeptic. If only climate debates were so straightforwardly resolved!
Do you understand why it’s ‘finite commutative semisimple rings’ which appear in your Hasse–Weil species (why those four terms and why the combination)? At zeta functions you say:
but that just shifts the question. In fact, don’t I recall considerable field-bashing over the years at the Café? Let’s see, we have James doing so here, and I’m sure you had a go at them at some point.
By the way, is there a connection back to week 218?
Yes, but I hadn’t finished writing that section of the paper yet, so I didn’t want to call attention to that connection. But there’s no keeping secrets from you. Now I have to get back to work.
In fact Jim came up with a lot of the new stuff after he finally read “week218”. I’d been hoping it would grow into something bigger, but I’d gotten stuck.
There’s a Math Overflow comment on Deninger’s work which says
Thanks, David. Yeah, I’d like to understand this better.
Here’s part of what I do understand:
A ‘discrete-time dynamical system’ is just a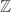 -set, and a
-set, and a 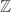 -set has a zeta function which I described back in "week218", but which turns out to be called the Artin-Mazur zeta function. The algebraic closure of
-set has a zeta function which I described back in "week218", but which turns out to be called the Artin-Mazur zeta function. The algebraic closure of 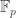 , called
, called  , becomes a discrete dynamical system thanks to the Frobenius automorphism
, becomes a discrete dynamical system thanks to the Frobenius automorphism
and the fixed points of the nth power of the Frobenius form the field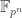 . This provides the link between the zeta functions of dynamical systems and zeta functions in number theory.
. This provides the link between the zeta functions of dynamical systems and zeta functions in number theory.
All this stuff is unmysterious to me, and I’ve almost managed to categorify the usual story.
But, there are also more tenuous and mysterious analogies between zeta functions in number theory and zeta functions of dynamical systems like flows on 3-manifolds. These rely in part on the fact that looks 3-dimensional viewed from the eyes of étale cohomology. You may recall me talking about this in "week257". The “Addenda” contain some extra useful hints. You’ll see the Frobenius plays a key role here, so it’s not as if this stuff is distinct from the stuff I understand. But I don’t have a good feeling for étale cohomology, so it seems more mysterious to me — even the part that Barry Mazur, say, would understand quite well.
looks 3-dimensional viewed from the eyes of étale cohomology. You may recall me talking about this in "week257". The “Addenda” contain some extra useful hints. You’ll see the Frobenius plays a key role here, so it’s not as if this stuff is distinct from the stuff I understand. But I don’t have a good feeling for étale cohomology, so it seems more mysterious to me — even the part that Barry Mazur, say, would understand quite well.
In a closed rig category, we typically have the isomorphism
where is the internal hom.
is the internal hom.
Since the data type of binary strings is defined to be
of binary strings is defined to be
where is the empty string, it ought to have cardinality -1 (it’s nicely isomorphic to the data type of three binary trees, and
is the empty string, it ought to have cardinality -1 (it’s nicely isomorphic to the data type of three binary trees, and 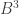 is nicely isomorphic to
is nicely isomorphic to  ), and therefore mapping out of
), and therefore mapping out of  acts like inversion:
acts like inversion:
In particular,
Binary trees are defined by


while binary strings are defined by
Triples of binary trees satisfy the isomorphism that defines binary strings:

Or you can reason as follows:
The paper by Marcelo Fiore and me, cited by John above, proves that this reasoning is valid. (And indeed, the proof embodies an algorithm for taking a chain of reasoning like mine and turning it into a chain of reasoning like yours.)
Yes, I love that paper! I was just trying to say that if your category is closed in addition to being a rig category, then you might be able to handle isomorphisms that involve exponentiation, like inverses.
We can implement this using rewrite rules.
An element of a binary tree can be written as a parenthesization of an expression built using multiplication and 1. Eg. 1((11)1)
Starting with such an expression we repeatedly use the rules below where
A -> b, C
means if your current expression matches A, output the number b, and make C the new current expression. It always terminates, consumes a tree, and eventually outputs the string of 0’s and 1’s that you want. This was derived directly from your algebraic derivation:
(ab, cd, ef) -> 0, (a, b, c(d(ef)))
(ab, cd, 1 ) -> 0, (a, b, c(d1))
(ab, 1, cd) -> 1, (a, b, cd)
(ab, 1, 1 ) -> 0, (a, b, 1)
(1, ab, cd) -> 0, (a, b, (cd)1)
(1, ab, 1 ) -> 0, (a, b, 11)
(1, 1, ab) -> 1, (a, b, 1)
(1, 1, 1) -> END
The rules are trivially confluent as only one rule can apply at each stage.
It’s easy to run in reverse too.
I was hoping there might be some neat geometrical picture showing how these trees pack together exactly to make bit strings. Haven’t figured one out yet.
(Everything modulo typos, of course.)
Thanks, Mike. I like the idea of bringing the closed structure/exponentiation into the game.
One other thing to note is that with groupoid cardinality, the groupoid is not isomorphic to
is not isomorphic to  ; it merely has the same cardinality. So using the inner hom as exponentiation is questionable when thinking about groupoid cardinality.
; it merely has the same cardinality. So using the inner hom as exponentiation is questionable when thinking about groupoid cardinality.
I’m glad to see that the end for s.p.r is also the
beginning of a new era.
You might consider stopping by Wave without a Shore
(CJ Cherryh)s blog the discussions are fairly eclectic
but involve lots of how to stuff on environment.
If you haven’t seen them yet. MIT video has a couple
by Nocera and Sadowsky worth looking at. These are
about how to store solar power for nocturnal usage.
Nocera is the third world (no power grid) and Sadowsky
is aimed at massive industrial grid solutions.
Thanks for you efforts over the years.
Why is the number of elements defined as 1/n! professor Baez?
I didn’t define any “number of elements” to be 1/n!. I said that if an object in a groupoid has some number of symmetries, we use the reciprocal of that number to say how much that object contributes to the “size” of that groupoid.
A set with n elements has n! symmetries: all the permutations of that set. So, in the groupoid of finite sets, any set with n elements contributes 1/n! to the size. And since all sets with n elements are isomorphic, we don’t count all of them separately — any one will do.
Why do we we take the reciprocal of the number of symmetries? This has lots of benefits: for example, it lets us take a 5-element set and “divide it by 2” and get a groupoid with size 5/2. Look at the picture here to see what I mean.
Wow, that was some TWF! The zeta function and groupoid cardinality, with loads of pointers to promising directions to take it further. You certainly chose a fitting theme for the finale.
Hi, Bruce. Thanks! I wanted to end on a high note, so I worked for weeks on this. The papers with Jim Dolan and Todd Trimble round out the story…
I hope to see more of you around here.
Zeta regularization can be also extended to integrals which are divergent and appear in Renormalization and quantum field theory i mean , here is the paper http://vixra.org/abs/1001.0042 in case someone is interested
, here is the paper http://vixra.org/abs/1001.0042 in case someone is interested