Networks and Population Biology (Part 1)

There are some tutorials starting today here:

• Tutorials on discrete mathematics and probability in networks and population biology, Institute of Mathematical Sciences, National University of Singapore, 2-6 May 2011. Organized by Andrew Barbour, Malwina Luczak, Gesine Reinert and Rongfeng Sun.

Rick Durrett is speaking on “Cancer modelling”. For his slides, see here, here and here. But here’s a quick taste:

Back in 1954, Armitage and Doll noticed that log-log plots of cancer incidence as a function of age are close to linear, except for breast cancer, which slows down in older women. They suggested an explanation: a chain of independent random events have to occur before cancer can start. A simple model based on a Markov process gives a simple formula for how many events it must take—see the first batch of slides for details. This work was the first of a series of ever more sophisticated multi-stage models of carcinogenesis.

One of the first models Durrett explained was the Moran process: a stochastic model of a finite population of constant size in which things of two types, say A and B are competing for dominance. I believe this model can be described by a stochastic Petri net with two states, A and B, and two transitions:

A + B \to A + A

and

A + B \to B + B

Since I like stochastic Petri nets, I’d love to add this to my collection.

Chris Cannings is talking about “Evolutionary conflict theory” and the concept of ‘evolutionary stable strategies’ for two-party games. Here’s the basic idea, in a nutshell.

Suppose a population of animals roams around randomly and whenever two meet, they engage in some sort of conflict… or more generally, any sort of ‘game’. Suppose each can choose from some set S of strategies. Suppose that if one chooses strategy i \in S and the other chooses strategy j \in S, the expected ‘payoff’ to the one is A_{ij}, while for the other it’s A_{ji}.

More generally, the animals might choose their strategies probabilistically. If the first chooses the ith strategy with probability \psi_i, and the second chooses it with probability \phi_i, then the expected payoff to the first player is

\langle \psi , A \phi \rangle

where the angle brackets are the usual inner product in L^2(S). I’m saying this in an overly fancy way, and making it look like quantum mechanics, in the hope that some bright kid out there will get some new ideas. But it’s not rocket science; the angle bracket is just a notation for this sum:

\langle \psi , A \phi \rangle = \sum_{i, j \in S} \psi_i A_{ij} \phi_j

Let me tell you what it means for a probabilistic strategy \psi to be ‘evolutionarily stable’. Suppose we have a ‘resident’ population of animals with strategy \psi and we add a few ‘invaders’ with some other strategy, say \phi. Say the fraction of animals who are invaders is some small number \epsilon, while the fraction of residents is 1 - \epsilon.

If a resident plays the game against a randomly chosen animal, its expected payoff will be

\langle \psi , A (\epsilon \phi + (1 - \epsilon) \psi) \rangle

Indeed, it’s just as if the resident was playing the game against an animal with probabilistic strategy \epsilon \phi + (1 - \epsilon) \psi! On the other hand, if an invader plays the game against a randomly chosen animal, its expected payoff will be

\langle \phi , A (\epsilon \phi + (1 - \epsilon) \psi) \rangle

The strategy \psi is evolutionarily stable if the residents do better:

\langle \psi , A (\epsilon \phi + (1 - \epsilon) \psi) \rangle \ge \langle \phi , A (\epsilon \phi + (1 - \epsilon) \psi) \rangle

for all probability distributions \phi and sufficiently small \epsilon > 0.

Canning showed us how to manipulate this condition in various ways and prove lots of nice theorems. His slides will appear online later, and then I’ll include a link to them. Naturally, I’m hoping we’ll see that a dynamical model, where animals with greater payoff get to reproduce more, has the evolutionary stable strategies as stable equilibria. And I’m hoping that some model of this sort can be described using a stochastic Petri net—though I’m not sure I see how.

On another note, I was happy to see Persi Diaconis and meet his wife Susan Holmes. Both will be speaking later in the week. Holmes is a statistician who specializes in “large, messy datasets” from biology. Lately she’s been studying ant networks! Using sophisticated image analysis to track individual ants over long periods of time, she and her coauthors have built up networks showing who meets who in ant ant colony. They’ve found, for example, that some harvester ants interact with many more of their fellows than the average ant. However, this seems to be due to their location rather than any innate proclivity. They’re the ants who hang out near the entrance of the nest!

That’s my impression from a short conversation, anyway. I should read her brand-new paper:

• Noa Pinter-Wollman, Roy Wollman, Adam Guetz, Susan Holmes and Deborah M. Gordon, The effect of individual variation on the structure and function of interaction networks in harvester ants, Journal of the Royal Society Interface, 13 April 2011.

She said this is a good book to read:

• Deborah M. Gordon, Ant Encounters: Interaction Networks and Colony Behavior, Princeton U. Press, Princeton New Jersey, 2010.

There are also lots of papers available at Gordon’s website.

This entry was posted on Monday, May 2nd, 2011 at 11:30 am and is filed under biology, mathematics, networks. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

14 Responses to Networks and Population Biology (Part 1)

  1. Tim van Beek says:
    2 May, 2011 at 12:03 pm

    In Heidelberg I once participated in a philosophical discussion about the meaning of “randomness” in mathematical probability theory, with all the statisticans arguing that there is no “randomness” in reality and that probability theory is just a model to handle situations with insufficient information.

    When I said that tossing a coin produces “random results” (I tried not to mention quantum mechanics, because the math people did not know anything about it), they mentioned a magician who later became a statistics professor who could toss a coin to land on the side he wanted, and could do the same thing with dice, too.

    After reading the Wikipedia article, I’m sure they must have meant Persi Diaconis. Can he really toss a coin in a way that does not look suspicious, and make it land on the side he wants?

    Reply
    • John Baez says:
      2 May, 2011 at 2:13 pm

      Yes, they must have been talking about Persi Diaconis—the only professor I know who left home at 14 to travel with a magician and learn the craft.

      I’ll ask him if he can make a coin land on the side he wants. For now, try this paper:

      • Persi Diaconis, Susan Holmes and Richard Montgomery, Dynamical bias in the coin toss.

      We analyze the natural process of flipping a coin which is caught in the hand. We prove that vigorously-flipped coins are biased to come up the same way they started. The amount of bias depends on a single parameter, the angle between the normal to the coin and the angular momentum vector. Measurements of this parameter based on high-speed photography are reported. For natural flips, the chance of coming up as started is about .51.

      Reply
    • David Corfield says:
      2 May, 2011 at 3:55 pm

      I remember chatting once with Persi at a conference in Mykonos about our mutual appreciation for Edwin Jaynes. Read chapter 10 of his book to convince yourself that randomness really isn’t in the world, save perhaps for quantum mechanics.

      …anyone familiar with the law of conservation of angular momentum can, after some practice, cheat as the usual coin-toss game and call his shots with 100 per cent accuracy. You can obtain any frequency of heads you want; and the bias of the coin has no influence at all on the results!

      Reply
      • Web Hub Tel says:
        3 May, 2011 at 2:09 am

        I get the exact opposite impression from reading Jaynes. In that chapter, he simply showed where Newtonian determinism becomes important. I say let the coin bounce on concrete and have them do the experiment again. :)

        Reply
      • John Baez says:
        3 May, 2011 at 3:00 am

        David wrote:

        Read chapter 10 of his book to convince yourself that randomness really isn’t in the world, save perhaps for quantum mechanics.

        In the real world quantum mechanics can’t always be cordoned off: chaos can amplify quantum randomness. But how important is this effect?

        I’ve never seen it studied for coin tosses. It’s possible that a few chaotic bounces could amplify quantum randomness to macroscopic levels… but I haven’t seen a calculation.

        I usually see people trying to calculate the maximum amount of time you could balance a pencil on its point, given that you can’t precisely specify both its position and momentum. Some physicist at Cornell estimates 3.5 seconds. John Florakis estimates 3.47 seconds (a suspiciously close answer!) D. Easton’s article raises a flag of caution, but I haven’t read it.

        In week223 I pointed out that Saturn’s moon Hyperion is interesting because it’s the only known moon that tumbles chaotically on a short time scale, thanks to its eccentric shape and gravitational interactions with Saturn and Titan. My guess (based on stuff I wrote earlier) is that it would take about 37 years for uncertainty at the quantum level to get amplified to a complete lack of knowledge about which way its axis of rotation is pointing. But there are important subtleties, as noted by Michael Berry:

        … the claim sometimes made, that chaos amplifies quantum indeterminacy, is misleading. The situation is more subtle: chaos magnifies any uncertainty, but in the quantum case ℏ has a smoothing effect, which would suppress chaos if this suppression were not itself suppressed by externally-induced decoherence, that restores classicality (including chaos if the classical orbits are unstable). The calculation in Appendix B shows this decoherence-induced classicalization more clearly for the illustrative example of Hyperion…

        Curiously, this paper by Berry was published by the Vatican in a volume entitled Quantum Mechanics: Scientific Perspectives on Divine Action.

        Reply
  2. Blake Stacey says:
    2 May, 2011 at 12:58 pm

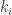    The subject of evolutionary game theory explodes into lovely complications when you realise that not everybody has to play everybody else at each turn. For some situations, a more realistic model might be an interaction network, where player i plays against the k_i others they are connected to, and what happens next depends on the scores earned in those games.

    G. Szabó and G. Fath (2007). “Evolutionary games on graphs“. Physics Reports 446, 4–6: 97–216. arXiv:cond-mat/0607344.

    Outcomes of the competition between strategies can depend on details of the “life cycle”; e.g., “birth-death” updating does not have the same result as “death-birth”.

    C. Tarnita et al. (2009). “Strategy selection in structured populations” Journal of Theoretical Biology 259: 570–81. PubMed:2710410.

    Reply
  3. Robert Smart says:
    2 May, 2011 at 7:41 pm

    Humanity’s stable evolutionary structure is not wimpy cooperativeness, which is not stable, but vigorous defence against non-cooperators. It seems likely that this has broken down in cities, but this possibly didn’t matter when cities were population sinks continuously refreshed by overflow from the country.

    Reply
  4. DavidTweed says:
    3 May, 2011 at 12:42 am

    Is there a typo after “We assume the game is symmetrical”: should it be A_{ij}=-A_{ji}? Otherwise swapping the strategies chosen by the two players doesn’t affect player 1’s “winnings”.

    I noticed that because I find it fascinating that very few people comment on how strong an assumption “We assume the game is symmetrical” is, and how tricky it is to justify that completely in non invented-game/financial situations. Often games are designed with some conserved quantity, often money, so that the amount one individual gains is equal to the amount another individual loses. However, in more general situations not all actions satisfy this constraint. Eg, let’s put on our leather jackets and take off our modern liberal values to go to a “Rebel without a cause” world where the winner of a game of chicken “gets the girl”. Even if we accept that the loser “loses his chance with one from a limited pool of girls”, so that we can argue there’s an appropriate notion of “player 1 winnings=-player 2 winnings”, there’s an extreme case where both players cut it too fine and go over the cliff. (Ok, this requires adding a probabilistic/skill/whatever ingredient to the model, but you get the point…) Then in that extreme case “player 1 winnings=player 2 winnings=loss of all future girl opportunities”, contrary to the general zero-sum balance in the game. So the (generalised) A matrix is no-longer either symmetrical or anti-symmmetrical but a mixture of both.

    The thing that I’m interested in is that clearly symmetries are a powerful constraints that happen to actually apply in most systems in “pure physics”, but do we use them in other models more because we like their power than because they’re justified?

    Reply
    • DavidTweed says:
      3 May, 2011 at 1:18 am

      Looking at the eventual wikipedia page on payoff matrixes, it seems like one common way to describe things is in terms of a pair of matrices A — describing player 1’s winnings from a pair of actions — and B — describing player 2’s winnings from a pair of actions. Although the framework seems perfectly capable of describing games where A and B are arbitrary, it’s interesting that all the examples I’ve found on wikipedia obey the rules A=B^T, so that the differential change (ie, how much better off player 1 is than player 2 after the encounter) matrix A-B is anti-symmetric matrix. In these relative terms the example above is still suitably anti-symmetric since if both go off the cliff there’s 0 relatitve change. I’m still suspicious of symmetries, although I can’t right now think of a situation where in these relative terms there’s an (anti-)symmetry violation.

      Reply
    • John Baez says:
      3 May, 2011 at 1:32 am

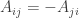      Thanks, David! I see from some examples that Cannings’ payoff matrices are neither symmetric (A_{ij} = A_{ji}) nor antisymmetric (A_{ij} = -A_{ji}).

      I know Cannings said something about the games being ‘symmetrical’. My math brain unthinkingly transcribed this remark into the equation A_{ij} = A_{ji}. But I think what he really means is that there’s no inherent concept of the ‘first player’ and ‘second player’ in the game.

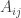      For example, two rams walk up to each other and start ramming each other. Each is free to pick any strategy, and if Rambo picks strategy i while Slambo picks strategy j, then Rambo’s expected winnings are A_{ij} while Slambo’s are A_{ji}. This is a simplification compared to the real world, because in the real world one ram might be designated the ‘defender of territory’ and one designated the ‘attacker’, and they might have different choices of strategies based on this, or different payoffs. If we drop this simplifying assumption we should use two matrices, as you explained.

      So, I’ll get rid of that equation! Thanks.

      Reply
  5. Networks and Population Biology (Part 2) « Azimuth says:
    4 May, 2011 at 2:07 pm

    In my last blog post on this conference Tim van Beek asked if Persi Diaconis could really flip a coin and have it land with whatever side up he wanted […]

    Reply
  6. Information Geometry (Part 8) « Azimuth says:
    26 May, 2011 at 9:45 am

    […] if you read my summary of Chris Canning’s talks on evolutionary game theory, you’ll see everything I just said meshes nicely with that.

    Reply

You can use Markdown or HTML in your comments. You can also use LaTeX, like this: $latex E = m c^2 $. The word 'latex' comes right after the first dollar sign, with a space after it.

This site uses Akismet to reduce spam. Learn how your comment data is processed.