Ice

Water is complicated and fascinating stuff! There are at least sixteen known crystal phases of ice, many shown in this diagram based on the work of Martin Chaplin:

(Click for a larger version.)

For example, ordinary ice is called ice I_h, because it has hexagonal crystals. But if you cool it below -37 °C, scientists believe it will gradually turn into a cubic form, called ice I_c. In this form of ice the water molecules are arranged like carbons in a diamond! And apparently some of it can be found in ice crystals in the stratosphere.

But if you wait longer, ice below -37 °C will turn into ice XI. The transformation process is slow, but ice XI has been found in Antarctic ice that’s 100 to 10,000 years old. This ice is ferroelectric, meaning that it spontaneously become electrically polarized, just like a ferromagnet spontaneously magnetizes.

That’s the usual textbook story, anyway. The true story may be even more complicated:

• Simon Hadlington, A question mark over cubic ice’s existence, Phys.org, 9 January 2012.

But now a team led by Benjamin Murray at the University of Leeds has carried out work that suggests that cubic ice may not in fact exist. The researchers searched for cubic ice by suspending water droplets in oil and gradually cooling them to -40 °C while observing the X-ray diffraction pattern of the resulting crystals. “We modelled the diffraction pattern we obtained and compared it to perfect cubic and perfect hexagonal ice, and it was clearly neither of them,” Murray says. “Nor is it merely a mixture of the two. Rather it is something quite distinct.”

Analysis of the diffraction data shows that in the ice crystals the stacking of the atomic layers is disordered. “The crystals that form have randomly stacked layers of cubic and hexagonal sequences,” Murray says. “As each new layer is added, there is a 50% probability of it being either hexagonal or cubic.” The result is a novel, metastable form of ice with a stacking-disordered structure.

Re-examination of what had previously been identified as cubic ice suggests that this was stacking-disordered structures too, Murray says. “Cubic ice may not exist.”

Even plain old ice I_h is surprisingly tricky stuff. The crystal structure is subtle, first worked out by Linus Pauling in 1935. Here’s a nice picture by Steve Lower:

There’s a lot of fun math here. First focus on the oxygen atoms, in red. What sort of pattern do they form?

Close-packings

To warm up for that question, it really helps to start by watching this video:

It’s not flashy, but it helped me understand something that had been bothering me for decades! This is truly beautiful stuff: part of the geometry of nature.

But I’ll explain ice I_h from scratch—and while I’m at it, ice I_c.

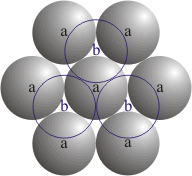
First we need to think about packing balls. Say you’re trying to pack equal-sized balls as densely as possible. You put down a layer in a hexagonal way, like the balls labelled ‘a’ here:

Then you put down a second hexagonal layer of balls. You might as well put them in the spots labelled ‘b’. There’s another choice, but the symmetry of the situation means it doesn’t matter which you pick!

The fun starts at the third layer. If you want, you can put these balls in the positions labelled ‘a’, directly over the balls in the first layer. And you can go on like this forever, like this:

-a-b-a-b-a-b-a-b-a-b-a-

This gives you the hexagonal close packing.

But there’s another choice for where to put the balls in the third layer… and now it does matter which choice you pick! The other choice is to put these balls in the spots labelled ‘c’:

And then you can go on forever like this:

-a-b-c-a-b-c-a-b-c-a-b-c-

This gives you the cubic close packing.

There’s also an uncountable infinity of other patterns that all give you equally dense packings. For example:

-a-b-a-c-b-a-c-b-c-b-a-c-

You just can’t repeat the same letter twice in a row!

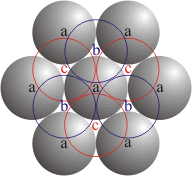
To review, here’s the difference between the hexagonal and cubic close packings:

But what’s ‘cubic’ about the cubic close packing? Well, look at this. At left we see a bit of a hexagonal close packing, while at right we see a bit of a cubic close packing:

The dashed white circle at right shows what you shouldn’t do for a cubic close packing. But the red lines at right show why it’s called ‘cubic’! If you grab that cube and pull it out, it looks like this:

As you can see, there’s a ball at each corner of a cube, but also one at the middle of each face. That’s why this pattern is also called a face-centered cubic.

If we shrink the balls a bit, the face-centered cubic looks like this:

What used to confuse me so much is that the cubic close packing looks very different from different angles. For example, when you see it like this, the cubical symmetry is hard to spot:

But it’s there! If you stack some balls in the hexagonal close packing, they look different:

And to my eye, they look uglier—they’re less symmetrical.

Anyway, perhaps now we’re in a better position to understand what Benjamin Murray meant when he said:

As each new layer is added, there is a 50% probability of it being either hexagonal or cubic.

I’m guessing that means that at each layer we randomly make either of the two choices I mentioned. I’m not completely sure. My guess makes the most sense if the ice is growing by accretion one layer at a time.

Diamonds

But there’s more to ice than close-packed spheres. If we ignore the hydrogen atoms and focus only on the oxygens, the two kinds of ice we’re talking about—the hexagonal ice I_h and the cubic ice I_c, assuming it exists—are just like two kinds of diamond!

The oxygens in ice I_c are arranged in the same pattern as carbons in an ordinary diamond:

This pattern is called a diamond cubic. We can get it by taking the cubic close packing, making the balls smaller, and then putting in new ones, each at the center of a tetrahedron formed by the old ones. I hope you can see this. There’s a ball at each corner of the cube and one at the center of each face, just as we want for a face-centered cubic. But then there are are 4 more!

But what about good old ice I_h? Here the oxygens are arranged in the same pattern as carbons in a hexagonal diamond.

You’ve heard about diamonds, but you might not have heard about hexagonal diamond, also known as lonsdaelite. It forms when graphite is crushed… typically by a meteor impact! It’s also been made in the lab.

Its crystal structure looks like this:

We get this pattern by taking a hexagonal close packing, making the balls smaller, and then putting in new ones, each at the center of a tetrahedron formed by the old ones. Again, I hope you can see this!

Entropy

Now we understand how the oxygens are arranged in good old ice I_h. They’re the red balls here, and the pattern is exactly like lonsdaelite, though viewed from a confusingly different angle:

But what about the hydrogens? They’re very interesting: they’re arranged in a somewhat random way!

Pick any oxygen near the middle of the picture above. It has 4 bonds to other oxygens, shown in green. But only 2 of these bonds have a hydrogen near your oxygen! The other 2 bonds have hydrogens far away, at the other end.

There are many ways for this to happen, and they’re all allowed—so ice is like a jigsaw puzzle that you can put together in lots of ways!

So, even though ice is a crystal, it’s disordered. This gives it entropy. Figuring out how much entropy is a nice math puzzle: it’s about 3/2 times Boltzmann’s constant per water molecule. Why?

Rahul Siddharthan explained this to me over on Google+. Here’s the story.

The oxygen atoms form a bipartite lattice: in other words, they can be divided into two sets, with all the neighbors of an oxygen atom from one set lying in the other set. You can see this if you look.

Focus attention on the oxygen atoms in one set: there are of them. Each has 4 hydrogen bonds, with two hydrogens close to it and two far away. This means there are

allowed configurations of hydrogens for this oxygen atom. Thus there are configurations that satisfy these atoms.

But now consider the remaining oxygen atoms: in general they won’t be satisfied: they won’t have precisely two hydrogen atoms near them). For each of those, there are

possible placements of the hydrogen atoms along their hydrogen bonds, of which 6 are allowed. So, naively, we would expect the total number of configurations to be

Using Boltzmann’s ideas on entropy, we conclude that

where is Boltzmann’s constant. This gives an entropy of 3.37 joules per mole per kelvin, a value close to the measured value. But this estimate is ‘naive’ because it assumes the 6 out of 16 hydrogen configurations for oxygen atoms in the second set can be independently chosen, which is false. More complex methods can be employed to better approximate the exact number of possible configurations, and achieve results closer to measured values.

By the way: I’ve been trying to avoid unnecessary jargon, but this randomness in ice I_h has such a cool name I can’t resist mentioning it. It’s called proton disorder, since the hydrogens I’ve been talking about are really just hydrogen nuclei, or protons. The electrons, which form the bonds, are smeared all over thanks to the wonders of quantum mechanics.

Higher pressures

If I were going to live forever, I’d definitely enjoy studying and explaining all sixteen known forms of ice. For example, I’d tell you the story of what happens to ordinary ice as we slowly increase the pressure, moving up this diagram until we hit ice XI:

Heck, I’d like to know what happens at every stage as we crush water down to neutronium! Unfortunately I’m mortal, with lots to do. So I recommend these:

• Martin Chaplin, Water phase diagram.

• Norman Anderson, The many phases of ice.

But there’s a bit of news I can’t resist mentioning…

Researchers at Sandia Labs in Albuquerque, New Mexico have been using the Z Machine to study ice. Here it is in operation, shooting out sparks:

Click for an even more impressive image of the whole thing.

How does it work? It fires a very powerful electrical current—about 20 million amps—into an array of thin, parallel tungsten wires. For a very short time, it uses a power of 290 terawatts. That’s 80 times the world’s total electrical power output! The current vaporizes the wires, and they turn into tubes of plasma. At the same time, the current creates a powerful magnetic field. This radially compresses the plasma tubes at speeds of nearly 100,000 kilometers per hour. And this lets the mad scientists who run this machine study materials at extremely high pressures.

Back in 2007, the Z Machine made ice VII, a cubic crystalline form of ice that coexists with liquid water and ice VI at 82 Celsius and about 20,000 atmospheres. Its crystal structure is theorized to look like this:

But now the Z Machine is making far more compressed forms of ice. Above 1 million atmospheres, ice X is stable… and above 8 million atmospheres, a hexagonal ferroelectric form called ice XI comes into play. This has a density over 2.5 times that of ordinary water!

Recent experiments with the Z Machine seem to show water is 30% less compressible than had been thought under conditions like those at the center of Neptune. These experiments seem to match new theoretical calculations, too:

• Experiments may force revision of astrophysical models: ice giant planets have more water volume than believed, Science Daily, 19 March 2012.

While it’s named after the Roman god of the seas, and it’s nice and blue, Neptune’s upper atmosphere is very dry. However, there seems to be water down below, and it has a heart of ice. A mix of water, ammonia and methane ice surrounding a rocky core, to be precise! But the pressure down there is about 8 million atmospheres, so there’s probably ice X and ice XI. And if that ice is less compressible than people thought, it’ll force some changes in our understanding of this planet.

Not that this matters much for most purposes. But it’s cool.

And if you don’t love math, this might be a good place to stop reading.

A little more math

Okay… if you’re still reading, you must want more! And having wasted the day on this post, I might as well explain a bit of the math of the crystal structures I described. I’ll want to someday; it might as well be now.

A lattice in n-dimensional Euclidean space is a subset consisting of all linear combinations of basis vectors. The centers of the balls in the cubic close packing form a lattice called the face-centered cubic or A₃ lattice. It’s most elegant to think of these as the vectors in 4-dimensional space having integer components and lying in the hyperplane

That way, you can see this lattice has the group of permutations of 4 letters as symmetries. Not coincidentally, this is the symmetry group of the cube.

In this description, you can take the three basis vectors to be

Note that they all have the same length and each lies at a 120° angle from the previous one, while the first and last are at right angles.

We can also get the A₃ lattice by taking the center of each red cube in a 3d red-and-black checkerboard. That means taking all vectors in 3-dimensional space with integer coefficients that sum to an even number. In this description, you can take the three basis vectors to be

This seems like an ugly choice, but note: they all have the same length and each lies at a 120° angle from the previous one, while the first and last are at right angles. So, we know it’s the A₃ lattice!

We see more symmetry if we look at all the shortest nonzero vectors in this description of the lattice:

These form the 12 midpoints of the edges of a cube, and thus the corners of a cuboctahedron:

So, in the cubic close packing each ball touches 12 others, centered at the vertices of a cuboctahedron, as shown here:

In the hexagonal close packing each ball also touches twelve others, but centered at the vertices of a mutant cuboctahedron whose top has been twisted relative to its bottom. This shape is called a triangular orthobicupola.

I should talk more about the lattice associated to the hexagonal close packing, but I don’t understand it well enough. Instead I’ll wrap up by explaining the math of the diamond cubic:

The diamond cubic is not a lattice. We can get it by taking the union of two copies of the A₃ lattice: the original lattice and a translated copy. For example, we can start with all vectors with integer coefficients summing to an even number, and then throw in all vectors This is called the D₃⁺ pattern.

The A₃ lattice gives a dense-as-possible packing of balls, the cubic close packing, with density

The D₃⁺ pattern, on the other hand, gives a way to pack spheres with a density of merely

This is why ordinary ice actually becomes denser when it melts. It’s not packed in the diamond cubic pattern: that would be ice I_c. Ordinary ice is packed in a similar pattern built starting from the hexagonal close packing! But the hexagonal close packing looks just like the cubic close packing if you only look at two layers… so this similar pattern gives a packing of balls with the same density as the diamond cubic.

Finally, for a tiny taste of some more abstract math: in any dimension you can define a checkerboard lattice called D_n, consisting of all n-tuples of integers that sum to an even integer. Then you can define a set called D_n⁺ by taking the union of two copies of the D_n lattice: the original and another shifted by the vector

D_n⁺ is only a lattice when the dimension n is even! When the dimension is a multiple of 4, it’s an integral lattice, meaning that the dot product of any two vectors in the lattice is an integer. It’s also unimodular, meaning that the volume of the unit cell is 1. And when the dimension is a multiple of 8, it’s also even, meaning that the dot product of any vector with itself is even.

Now, D₈⁺ is very famous: it’s the only even unimodular lattice in 8 dimensions, and it’s usually called E₈. In week193, I showed you that in the packing of balls based on this lattice, each ball touches 240 others. It’s extremely beautiful.

But these days I’m trying to stay more focused on the so-called ‘real world’ of chemistry, biology, ecology and the like. This has a beauty of its own. In 3 dimensions, D₃ = A₃ is the face-centered cubic. D₃⁺ is the diamond lattice. So, in a way, diamonds come as close to E₈ as possible in our 3-dimensional world.

The diamond cubic may seem mathematically less thrilling than E₈: not even a lattice. Ordinary ice is even more messy. But it has a different charm—the charm of lying at the bordeline of simplicity and complexity—and the advantage of manifesting itself in the universe we easily see around us, with a rich network of relationships to everything else we see.