There’s a lot more to say, but just one more class to say it! Next quarter I’ll be busy teaching an undergraduate course on evolutionary game theory and a grad course on Lagrangian methods in classical mechanics, together with this seminar and weekly meetings with my students. So, to keep from burning out, I’m going to temporarily switch this seminar to a different topic, where I have a textbook all lined up:
• John Baez and Jacob Biamonte, A Course on Quantum Techniques in Stochastic Mechanics.
I will stop putting up online notes. I’ll also teach the classical mechanics using a book I helped write:
• John Baez and Derek Wise, Lectures on Classical Mechanics.
This should make my job a bit easier: explaining climate physics is a lot more work, since I’m just an amateur! But I hope to come back to this topic someday.
In this final class let’s talk a bit about recent work on glacial cycles and changes in the Earth’s orbit. To keep my job manageable, I’ll just talk about one paper.
The work of Didier Paillard
We’ve seen a few puzzles about how Milankovich cycles are related to the glacial cycles. There are many more I haven’t even gotten around to explaining:
• Milankovich cycles: problems, Wikipedia.
But let’s dive in and look at a model that tries to solve some:
• Didier Paillard, The timing of Pleistocene glaciations from a simple multiple-state climate model, Nature 391 (1998), 378–391.
Paillard starts by telling us the good news:
The Earth’s climate over the past million years has been characterized by a succession of cold and warm periods, known as glacial–interglacial cycles, with periodicities corresponding to those of the Earth’s main orbital parameters; precession (23 kyr), obliquity (41 kyr) and eccentricity (100 kyr). The astronomical theory of climate, in which the orbital variations are taken to drive the climate changes, has been very successful in explaining many features of the palaeoclimate records.
I’m not including reference numbers, but here he cites a famous paper which we discussed in Part 8:
• J. D. Hays, J. Imbrie, and N. J. Shackleton, Variations in the earth’s orbit: pacemaker of the Ice Ages, Science 194 (1976), 1121–1132.
The main result of this paper was to find peaks in the power spectrum of various temperature proxies that match some of the periods of the Milankovitch cycles. This has repeatedly been confirmed. In fact, one of the students in this course, Blake Pollard, has already checked this. I want to pressure him to write a blog article including the nice graphs he’s generated.
But then comes the bad news:
Nevertheless, the timing of the main glacial and interglacial periods remains puzzling in many respects. In particular, the main glacial–interglacial switches occur approximately every 100 kyr, but the changes in insolation forcing are very small in this frequency band.
Here’s an article on the first problem:
• 100,000-year problem, Wikipedia.
The basic idea is that during the last million years, the glacial cycles seem to happening roughly every 100 thousand years:
The Milankovich cycles that most closely match this are two cycles in the eccentricity of the Earth’s orbit which have periods of 95 and 123 thousand years. But as we saw last time, these have very tiny effects on the average solar energy hitting the Earth year round. The obliquity and precession cycles have no effect on the average solar energy hitting the Earth, but they have a noticeable effect on how much hits it in a given latitude in a given season!
Alas, we didn’t get around to calculating that yet. But this gives you a sense of it:
As common in paleontology, time here goes from right to left. The yellow curve shows the amount of solar power hitting the Earth at a latitude of 65° N at the summer solstice. This quantity is often called simply the insolation, though that term also means other things. The insolation curve most closely resembles the red curve showing precession cycles, which have periods near 20 thousand years. But during this stretch of time, ice ages have been happening roughly once every 100 thousand years! Why? That’s the 100,000 year problem.
Continuing the quotation:
Similarly, an especially warm interglacial episode, about 400,000 years ago, occurred at a time when insolation variations were minimal.
If you look at the graph above, you’ll see what he means.
Next, he sketches what he’ll do:
Here I propose that multiple equilibria in the climate system can provide a resolution of these problems
within the framework of astronomical theory. I present two simple models that successfully simulate each glacial–interglacial cycle over the late Pleistocene epoch at the correct time and with approximately the correct amplitude. Moreover, in a simulation over the past 2 million years, the onset of the observed prominent 100-kyr cycles around 0.8 to 1 million years ago is correctly reproduced.
Paillard’s model
I’ll just talk about his first, simpler model. It assumes the Earth can be in three different states:
• i: interglacial
• g: mild glacial
• G: full glacial
In this model:
• The Earth goes from i to g as soon as the insolation goes below some level
• The Earth then goes from g to G as soon as the volume of ice goes above some level
• The Earth then goes from G to i as soon as the insolation goes above some level
Only the transitions i → g and g → G are allowed! The reverse transitions G → g and g → i are forbidden. Paillard draws a schematic picture of the model, like this:
Of course, he also most specify how the ice volume grows when the Earth is in its mild glacial g state. He says:
I assume that the ice sheet needs some minimal time
in order to grow and exceed the volume
[…] and that the insolation maxima preceding the g–G transition must remain below the level
The g–G transition then can occur at the next insolation decrease, when it falls below
.
Being a mathematician rather than a climate scientist, I can think of more than one way to interpret this. I think it means:
1. If the Earth is in its g state and the insolation stays below some value 
2. If the Earth is in its g state and the insolation rises above 
An alternative interpretation is:
2′. If the Earth is in its g state and the insolation rises above 
I’ll try to sort this out. Now, the insolation as a function of time is known—you can compute it using the formula and the data here:
• Insolation, Azimuth Project.
So, the only thing required to complete Paillard’s model are choices of these numbers:
He likes to measure insolation in terms of its standard deviation from its mean value. With this normalization he takes:
and
Then his model gives these results:
(Click to enlarge.) The bottom graph shows temperature as measured by the extra amount of oxygen-18 in some geological records. So, we can see that the Earth often pops rather suddenly into a warm interglacial state and cools a bit more slowly into a glacial state. In the model, this ‘popping into a warm state’ happens instantaneously in the middle graph. The main thing is to compare this to the bottom graph!
It looks quite good! So, I want to think about this type of model more.
The way the models pops suddenly into the very cold G state does not look quite so good. But still, it’s exciting how such a simple model fits the overall profile of the glacial cycle—at least for the last million years.
Paillard says his model is fairly robust, too:
This model is not very sensitive to parameter changes. Different threshold values will slightly offset the transitions by a few hundred years, but the overall shape will remain the same for a broad range of values. There is no significant changes when
is between -0.97 and -0.64,
between -0.23 and 0.32,
Marine isotope stages
There’s a lot more to say. For example, what does the model say about the time more than a million years ago, when the glacial cycles happened roughly every 41 thousand years, instead of every 100? I won’t answer this. Instead, I’ll conclude by explaining something very basic—but worth knowing.
What’s ‘stage 11.3’? This refers to the numbers down at the bottom of Paillard’s chart: these numbers are Marine Isotope Stages. 11.3 is a ‘substage’, not shown on the chart.
Marine Isotopes Stages are official periods of time used by people who study glacial cycles. The even-numbered ones roughly correspond to glacial periods, and the odd-numbered ones to interglacials. By now over a hundred stages have been identified, going back 6 million years!
Just to give you a little sense of what’s going on, here are the start dates of the last 11 stages, with hot ones in red and the cold ones in blue:
• MIS 1: 11 thousand years ago. This marks the end of the last glacial cycle. More precisely, this is about 500 years after the end of the Younger Dryas event.
• MIS 2: 24 thousand years ago. The Last Glacial Maximum occurred between 26.5 and 19 thousand years ago. At that time we had ice sheets down to the Great Lakes, the mouth of the Rhine, and covering the British Isles. Homo sapiens arrived in the Americas later, around 18 thousand years ago.
• MIS 3: 60 thousand years ago. For comparison, Homo sapiens arrived in central Asia around 50 thousand years ago. About 35 thousand years ago the calendar was invented, Homo sapiens arrived in Europe, and Homo neanderthalensis. went extinct.
• MIS 4: 71 (or maybe 74) thousand years ago.
• MIS 5: 130 thousand years ago. The Eemian, the last really warm interglacial period before ours, began at this time and ended about 114 thousand years ago. If you look at this chart, you’ll see MIS 3 was a much less warm interglacial:
(Now time is going to the right again. Click for more details.)
• MIS 6: 190 thousand years ago.
• MIS 7: 244 thousand years ago. The first known Homo sapiens date back to 250 thousand years ago.
• MIS 8: 301 thousand years ago.
• MIS 9: 334 thousand years ago.
• MIS 10: 364 thousand years ago. The first known Homo neanderthalensis date back to about 350 thousand years ago.
• MIS 11: 427 thousand years ago. This stage is supposedly the most similar to MIS 1, and looking at the graph above you can see why people say that.
I hope you agree that it’s worth understanding the glacial cycles, not just because we need to understand how the Earth will respond to the big boost of carbon dioxide that we’re dosing it with now, but because it’s a fascinating physics problem—and because glaciation has been a powerful force in Earth’s recent history, and the history of our species.
Table of Contents
For your convenience, here are links to all the notes for this course:
- Part 1 – The mathematics of planet Earth.
- Part 2 – Simple estimates of the Earth’s temperature.
- Part 3 – The greenhouse effect.
- Part 4 – History of the Earth’s climate.
- Part 5 – A model showing bistability of the Earth’s climate due to the ice albedo effect: statics.
- Part 6 – A model showing bistability of the Earth’s climate due to the ice albedo effect: dynamics.
- Part 7 – Stochastic differential equations and stochastic resonance.
- Part 8 – A stochastic energy balance model and Milankovitch cycles.
- Part 9 – Changes in insolation due to changes in the eccentricity of the Earth’s orbit.
- Part 10 – Didier Paillard’s model of the glacial cycles.
Azimuth 
From the part you quoted, it sounds to me like the g-G transition requires the temperature to fall below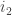
, and also to have been below 
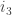for a time 
.
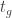In other words, the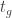
timer starts running when we enter the g state and resets whenever it gets warmer than 
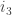; once the timer runs out, the next time it gets colder than 
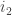, we transition to G.
There was an interesting article in New Scientist recently (“The Great Thaw”, 3 Nov 2012, p.32) covering some work by Shakun et al. in Nature (vol 484, p 49), suggesting quite a complex series of events in the transition out of the last ice age about 20,000 years ago.
Starting from an increase in northern summer sunshine and some melting of arctic ice, there was a slowdown in the Atlantic conveyor current due to the reduced salinity, which cooled the northern hemisphere but warmed the southern hemisphere. Consequent changes in winds and currents then brought more deep water to the surface of the Southern Ocean, releasing trapped CO2 and warming the whole planet.
The general idea, if I’ve understood this correctly, is that it seems initially mysterious that we have word-wide ice ages rather than northern/southern ones, given that increased summer sunshine in one hemisphere means a reduction in the other. And the proposed solution to the puzzle involves transitions in ocean circulation patterns and ocean storage of CO2.
Hopefully the extra CO2 is enough to avert the next ice age.
There’s been a lot of work on this, discussed very nicely here:
• Andrew Revkin, The next age and the Anthropocene, Dot Earth, 8 January 2012.
The consensus seems to be that we have put enough CO2 into the air to postpone the next glacial period, perhaps for the next 100,000 years. And this paper:
• Gary Schaffer, Long time management of fossil fuel resources to limit global warming and avoid ice age onsets, Geophys. Res. Lett. 36 (2009), L03704.
suggests that we if we save our remaining fossil fuels, we could head off the next few glacial cycles by burning them at appropriately chosen times. Another possibility would be to deliberately release more potent greenhouse gases than CO2 whenever a glacial period was imminent.
If we were smart, we might be able to manage the Earth’s temperature for quite a while, avoiding glacial periods without turning up the heat full blast as we’re doing now.
I asked Didier Paillard:
He replied:
The problem with Paillard’s model is that it doesn’t explain anything. It certainly doesn’t explain the most prominent features of the current Ice Age — Dansgaard/Oeschger and Heinrich events. It needs to explain why throughout most of Earth’s 4.5By history, it has only seen four Ice Ages, despite insolation starting out 30% lower than it is today. Paillard’s touches on none of this, it is an oversimplification that doesn’t work when extended to all of Earth’s history instead of just recent history.
I’ve seen many Ice Age models, not just this one of Paillard’s. Some of these other models actually do try to explain how Ice Ages are caused and when they will begin and end. My favorite (but still flawed) model at the moment is Sea ice switch mechanism and glacial-interglacial CO2 variations by Hezi Gildor and Eli Tziperman.
It’s interesting that so many people think that the only thing that determines climate on the Earth is the Sun, yet when you look around, you can see this isn’t true. For example, desert climates are not caused by the Sun, they are determined by proximity to mountain shadows. Arctic climates are determined by latitude. Some climates are determined by altitude, and so on. The Sun provides the energy for WEATHER but geophysical context determines CLIMATE. (I guess while I’m on this soapbox, another thing that interests me is the belief that higher temperatures everywhere mean greater storm intensity. That’s nonsense. It is temperature DIFFERENCE that determines storm intensity, and higher temperatures everywhere means higher temperatures everywhere, not in just one place).
By the way, I think you would like reading An Assessment of Climate Feedbacks in Coupled Ocean–Atmosphere Models by Brian J. Soden and Isaac M. Held as well as Conceptual Models of the Climate: 2001 Program of Study in Geophysical Fluid Dynamics, before making your next post on mathematics and climate.
Also, I want you remember that CO2 only accounts for 3% of the current Greenhouse effect, so what accounts for the rest of the Greenhouse effect? I know what it is but I wonder why very few people ever attempt to talk about that? I want you to return back to a discussion on radiation balance after taking a look at figure 4-1 at http://www.ssec.wisc.edu/library/coursefiles/04_rad_budget.pdf. It is an extremely common pictorial of the Earth’s radiation budget in visual form. Can you calculate Earth’s current temperature using just that figure alone? I can, it is a very elementary exercise and you would think that everyone would use the empirical description of the Earth’s radiation budget in that figure to base their models on, but they don’t. It is an empirical observation that tells us everything we need to know on how to calculate Earth’s current temperature so how can people in-the-know ignore such an elementary thing and yet still claim to be in-the-know?
[…] 2012/12/04: JCBaez: Mathematics of the Environment (Part 10) […]
What happens when you run the model forwards?
My student Michael Knap plans to write software for this model, and then it’ll be easy to answer that question (if, umm, we can get future insolation data—but I think we can). Sounds fun! If he does it, we’ll announce it here.
There are also much more detailed efforts to predict the start of the next glacial cycle, like this.
At the Azimuth Code Project, we are aiming to produce educational software that is relevant to the Earth sciences and the study of climate. Our present software takes the form of interactive web pages, which allow you to experiment with the parameters of models and view their outputs. But to fully understand the meaning of a program, we need to know about the concepts and theories that inform it. So we will be writing articles to explain both the programs themselves and the math and science behind them.
In this two-part series, I’ll cover the Azimuth stochastic resonance example program, by Allan Erskine and Glyn Adgie. In the Azimuth blog article Increasing the Signal-to-Noise Ratio with More Noise, Glyn Adgie and Tim van Beek give a nice explanation of the idea of stochastic resonance, which includes some clear and exciting graphs.