Last time we classified games in a few ways. This time we’ll start by looking at a very simple class of games: simultaneous noncooperative two-player games.
Simultaneous games
Remember that in a simultaneous game, each player makes their moves without knowing anything about the other player’s move. Thanks to this, we can condense each player’s move into a single move. For example, in a card game, if one player lays down a king and then an ace, we can mathematically treat this as a single move, called “lay down a king and then an ace”. So, we’ll say each player makes just one move—and they make it without knowing the other player’s move.
In class we’ll play these games like this. I will decide on my move and write it down on a piece of paper. You’ll make your move and click either A,B,C,D, or E on your clicker.

Then I’ll reveal my piece of paper! At that point, we’ll each know what both of us did… but neither of us can change our move.
So, we each make our move without knowing each other’s move.
Two-player games
Since lots of you will be clicking your clicker at once, you could say there are more than two players in this game. But your payoff—the number of points you win or lose—will depend only on what you did and what I did. So, we can treat this game as a bunch of independent two-player games—and that’s what we’ll do.
Noncooperative games
Remember, we use words in funny ways in mathematics! An ‘imaginary’ number is not imaginary in the usual sense; a ‘partial’ differential equation isn’t just part of a differential equation, and so on. In game theory we use the word ‘noncooperative’ in a funny way. We say a game is noncooperative if the players aren’t able to form binding commitments. This means that when we play our games, you and I can’t talk before the game and promise to do certain things.
There will, however, be games where both of us win if we make the right choice, and both of us lose if we don’t! In games like this, if we can figure out how to cooperate without communicating ahead of time and making promises, that’s allowed!
Chicken
Now let’s actually look at an example: the game of chicken. In this game we drive toward each other at high speed along a one-lane road in the desert. The one who swerves off the road at the last minute gets called a chicken, and the other driver gets called a hero. If we both swerve off the road at the last minute, we’re both called chickens. But if neither of us does, our cars crash and we both die!
Sounds fun, eh?
In real life we could each wait as long as possible and see if the other driver starts to swerve. This makes chicken into a sequential rather than simultaneous game! You could also promise that you wouldn’t swerve. This makes chicken into a cooperative game!
Indeed there are all sorts of variations and complications in real life. You can see some in the famous movie Rebel Without a Cause, starring James Dean. Take a look at what happens:
This movie version actually involves driving toward a cliff and jumping out at the last possible moment.
But mathematics, as usual, is about finding problems that are simple enough to state precisely. So in our simple mathematical version of chicken, we’ll say each player has just two choices:
1: stay on the road.
2: swerve off the road at the last second.
Also, we’ll express our payoffs in terms of numbers. A negative payoff is bad, a positive one is good:
• If either player swerves off the road they get called a chicken, which is bad, so let’s say they get -1 points.
• If one player stays on the road and other swerves off the road, the one who stays on the road gets called a hero, so let’s say they get 1 point.
• If both players stay on the road they both die, so let’s say they both get -10 points.
We can summarize all this in a little table:
| 1 | 2 | |
| 1 | (-10,-10) | (1,-1) |
| 2 | (-1,1) | (-1,-1) |
Let’s say the players are you and me. Your choices 1 and 2 are shown in in black: you get to pick which row of the table we use. My choices 1 and 2 are in red: I get to pick which column of the table we use.
There are four possible ways we can play the game. For each of the four possibilities we get a pair of numbers. The first number, in black, is your payoff. The second, in red, is my payoff.
For example, suppose you choose 1 and I choose 2. Then you’re a hero and I’m a chicken. So, your payoff is 1 and mine is -1. That’s why we get the pair of numbers (1,-1) in the 1st row and 2nd column of this table.
Now let’s play this game a bit! Later we’ll study it in different ways.
Rock-paper-scissors
Here’s another famous game: rock-paper-scissors.
Each player can choose either rock, paper or scissors. Paper beats rock, scissors beats paper, and rock beats scissors. In these cases let’s say the winner gets a payoff of 1, while the loser gets a payoff of -1. If both players make the same choice, it’s a tie, so let’s say both players get a payoff of 0.
Here’s a table that describes this game:
| rock | paper | scissors | |
| rock | (0,0) | (-1,1) | (1,-1) |
| paper | (1,-1) | (0,0) | (-1,1) |
| scissors | (-1,1) | (1,-1) | (0,0) |
Your choices and payoffs are in black, while mine are in red.
For example, if you choose rock and I choose paper, we can look up what happens, and it’s (-1,1). That means your payoff is -1 while mine is 1. So I win! ![]()
To make this table look more mathematical, we can make up numbers for our choices:
1: rock
2: paper
3: scissors
Then the table looks like this:
| 1 | 2 | 3 | |
| 1 | (0,0) | (-1,1) | (1,-1) |
| 2 | (1,-1) | (0,0) | (-1,1) |
| 3 | (-1,1) | (1,-1) | (0,0) |
Let’s play this game a bit, and then discuss it!
Normal form
In the games we’re studying now, each player can make various choices. In game theory these choices are often called pure strategies. We’ll see why later on in this course.
In our examples so far, each player has the same set of pure strategies. But this is not required! You could have some set of pure strategies and I could have some other set.
For now let’s only think about games where we both have a finite set of pure strategies. For example, you could have 4 pure strategies and I could have 2. Then we could have a game like this:
| 1 | 2 | |
| 1 | (0,0) | (-1,1) |
| 2 | (2,-1) | (0,0) |
| 3 | (-2,1) | (1,-1) |
| 4 | (0,1) | (2,0) |
This way of describing a game using a table of pairs of numbers is called normal form, and you can read about it here:
• Normal-form game, Wikipedia.
There are other ways to describe the same information. For example, instead of writing
| 1 | 2 | |
| 1 | (0,0) | (-1,1) |
| 2 | (2,-1) | (0,0) |
| 3 | (-2,1) | (1,-1) |
| 4 | (0,1) | (2,0) |
we can write everything in black:
| 1 | 2 | |
| 1 | (0,0) | (-1,1) |
| 2 | (2,-1) | (0,0) |
| 3 | (-2,1) | (1,-1) |
| 4 | (0,1) | (2,0) |
All the information is still there! It’s just a bit harder to see. The colors are just to make it easier on you.
Mathematicians like matrices, which are rectangular boxes of numbers. So, it’s good to use these to describe normal-form games. To do this we take our table and chop it into two. We write one matrix for your payoffs:
and one for mine:
The number in the ith row and jth column of the matrix is called
, and similarly for
. For example, if you pick choice 3 in this game and I pick choice 2, your payoff is
and my payoff is
Definition
Let’s summarize everything we’ve learned today! Remember, an matrix has
rows and
columns. So, we can say:
Definition. A 2-player normal-form game consists of two matrices of real numbers,
and
This definition is very terse and abstract. That’s what mathematicians like! But we have to unfold it a bit to understand it.
Let’s call you ‘player A’ and me ‘player B’. Then the idea here is that player A can choose among pure strategies while player B can choose among pure strategies
Suppose player A makes choice
and player B makes choice
Then the payoff to player A is
and the payoff to player B is


Since this blog is focused a lot on biology and life sciences, and saving our planet, I wanted to mention something that I think will get some of your students, and even a few readers here excited. It’s the so-called rock-paper-scissor mechanism, common in side-blotched lizards:
• Blotched lizard: rock-paper-scissor mechanism, Wikipedia.
In short, the lizards have three distinct color morphs: each with different physical traits and different mating behaviour.
And the population of each morph varies in time; this has been going on for a long long time.
That’s really cool! When I finally hook up these ideas with evolutionary game theory—which may or may not happen in this class—it’ll be fun to study this example! And when I explain how evolutionary game theory is connected to stochastic Petri nets—which definitely won’t happen in this class—you’ll get to see how everything I’m doing is related to everything else!
By the way: the payoff matrix for the rock-paper-scissors game is a bit similar to the Levi–Civita tensor:
for the rock-paper-scissors game is a bit similar to the Levi–Civita tensor:
Surely this fact has got to be good for something! The evolution of blotched lizard swirls and ‘curls’ around as time passes…
Permutations? (The Levi-Civita tensor/symbol looks like “non-abstract” nonsense to me. It might have some formalist benefit for non-formalists who insist on thinking geometry/tensor algebra in coordinates. Is it any good except for maximizing index mess and to strain IQ?)
In three dimensions, the Levi-Civita tensor is:
is:
•1 when the indices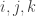 (which range from 1 to 3) form an even permutation,
(which range from 1 to 3) form an even permutation,
• -1 when they form an odd permutation
• 0 otherwise.
So, the vector cross product is given by
where we sum over repeated indices.
In two dimensions the same idea gives a Levi–Civita tensor ; in four it gives
; in four it gives  , and so on… but only in three does it give us a cross product. In general it gives us a volume form. All this stuff is very important in geometry and can be discussed at many different levels of sophistication.
, and so on… but only in three does it give us a cross product. In general it gives us a volume form. All this stuff is very important in geometry and can be discussed at many different levels of sophistication.
The payoff matrix for the rock-paper-scissors game is not the Levi–Civita tensor; it’s something related but a bit mysterious to me!
There are also http://en.wikipedia.org/wiki/Nontransitive_dice !
Hi!
Cool post!
Thanks! Glad to know you’re out there somewhere reading these. I fixed that typo.
John, in the new (relatively speaking) BBC series “Sherlock” the first episode is called “A Study In Pink”. The killer plays a two-person, zero sum game as the climax…
I think I have that episode on a DVD somewhere!
IMO this analysis of the chicken game doesn’t really capture it’s essence. The player strategies are not about binary choices between staying or swerving (even if that is the final outcome), rather they are about how long they are willing to stay on the road before swerving. The difference is that when expressed in this way there is an optimal strategy – stay until the time to collision is equal to the time your car needs to clear the road and not hit the other car. Of course that is certainly not easy to do in practice but still.
As I mentioned, the simplified chicken game discussed here is a ‘simultaneous’ game, where both players make a single move simultaneously. It’s already fascinating, as you can see in the analysis here:
• Chicken game, Wikipedia.
It seems that among game theorists the simultaneous version of chicken is ‘the’ game of chicken. The game reckless teenagers play with cars is a ‘sequential’ game of a ‘continuous’ sort: the players don’t take turns, they’re both observing each other at every moment and making their decisions based on what they say. Pretty much every interesting feature of the simultaneous version shows up in the sequential version—and more.
For example, both versions raise the issue of ‘pre-commitment’:
Whoops!
Is it possible for rock-paper-scissors to be a multiplayer game? In this case, wouldn’t it be a non-zero sum game?
It depends on how you generalize it to be a multiplayer game. How would you do it? For example, what happens if Alice says “rock”, Bob says “paper” and Charles says “scissors”?
You need to introduce more than 3 options.
Last time we started looking at 2-player normal form games. Now we’ll talk about the concept of ‘Nash equilibrium’ […]