John Harte is an ecologist who uses maximum entropy methods to predict the distribution, abundance and energy usage of species. Marc Harper uses information theory in bioinformatics and evolutionary game theory. Harper, Harte and I are organizing a workshop on entropy and information in biological systems, and I’m really excited about it!
It’ll take place at the National Institute for Mathematical and Biological Synthesis in Knoxville Tennesee. We are scheduling it for Wednesday-Friday, April 8-10, 2015. When the date gets confirmed, I’ll post an advertisement so you can apply to attend.
Writing the proposal was fun, because we got to pull together lots of interesting people who are applying information theory and entropy to biology in quite different ways. So, here it is!
Proposal
Ever since Shannon initiated research on information theory in 1948, there have been hopes that the concept of information could serve as a tool to help systematize and unify work in biology. The link between information and entropy was noted very early on, and it suggested that a full thermodynamic understanding of biology would naturally involve the information processing and storage that are characteristic of living organisms. However, the subject is full of conceptual pitfalls for the unwary, and progress has been slower than initially expected. Premature attempts at ‘grand syntheses’ have often misfired. But applications of information theory and entropy to specific highly focused topics in biology have been increasingly successful, such as:
• the maximum entropy principle in ecology,
• Shannon and Rényi entropies as measures of biodiversity,
• information theory in evolutionary game theory,
• information and the thermodynamics of individual cells.
Because they work in diverse fields, researchers in these specific topics have had little opportunity to trade insights and take stock of the progress so far. The aim of the workshop is to do just this.
In what follows, participants’ names are in boldface, while the main goals of the workshop are in italics.
Roderick Dewar is a key advocate of the principle of Maximum Entropy Production, which says that biological systems—and indeed all open, non-equilibrium systems—act to produce entropy at the maximum rate. Along with others, he has applied this principle to make testable predictions in a wide range of biological systems, from ATP synthesis [DJZ2006] to respiration and photosynthesis of individual plants [D2010] and plant communities. He has also sought to derive this principle from ideas in statistical mechanics [D2004, D2009], but it remains controversial.
The first goal of this workshop is to study the validity of this principle.
While they may be related, the principle of Maximum Entropy Production should not be confused with the MaxEnt inference procedure, which says that we should choose the probabilistic hypothesis with the highest entropy subject to the constraints provided by our data. MaxEnt was first explicitly advocated by Jaynes. He noted that it is already implicit in the procedures of statistical mechanics, but convincingly argued that it can also be applied to situations where entropy is more ‘informational’ than ‘thermodynamic’ in character.
Recently John Harte has applied MaxEnt in this way to ecology, using it to make specific testable predictions for the distribution, abundance and energy usage of species across spatial scales and across habitats and taxonomic groups [Harte2008, Harte2009, Harte2011]. Annette Ostling is an expert on other theories that attempt to explain the same data, such as the ‘neutral model’ [AOE2008, ODLSG2009, O2005, O2012]. Dewar has also used MaxEnt in ecology [D2008], and he has argued that it underlies the principle of Maximum Entropy Production.
Thus, a second goal of this workshop is to familiarize all the participants with applications of the MaxEnt method to ecology, compare it with competing approaches, and study whether MaxEnt provides a sufficient justification for the principle of Maximum Entropy Production.
Entropy is not merely a predictive tool in ecology: it is also widely used as a measure of biodiversity. Here Shannon’s original concept of entropy naturally generalizes to ‘Rényi entropy’, which depends on a parameter 
where 
As 
John Baez has explained the role of Rényi entropy in thermodynamics [B2011], and together with Tom Leinster and Tobias Fritz he has proved other theorems characterizing entropy which explain its importance for information processing [BFL2011]. However, these ideas have not yet been connected to the widespread use of entropy in biodiversity studies. More importantly, the use of entropy as a measure of biodiversity has not been clearly connected to MaxEnt methods in ecology. Does the success of MaxEnt methods imply a tendency for ecosystems to maximize biodiversity subject to the constraints of resource availability? This seems surprising, but a more nuanced statement along these general lines might be correct.
So, a third goal of this workshop is to clarify relations between known characterizations of entropy, the use of entropy as a measure of biodiversity, and the use of MaxEnt methods in ecology.
As the amount of data to analyze in genomics continues to surpass the ability of humans to analyze it, we can expect automated experiment design to become ever more important. In Chris Lee and Marc Harper’s RoboMendel program [LH2013], a mathematically precise concept of ‘potential information’—how much information is left to learn—plays a crucial role in deciding what experiment to do next, given the data obtained so far. It will be useful for them to interact with William Bialek, who has expertise in estimating entropy from empirical data and using it to constrain properties of models [BBS, BNS2001, BNS2002], and Susanne Still, who applies information theory to automated theory building and biology [CES2010, PS2012].
However, there is another link between biology and potential information. Harper has noted that in an ecosystem where the population of each type of organism grows at a rate proportional to its fitness (which may depend on the fraction of organisms of each type), the quantity
always decreases if there is an evolutionarily stable state [Harper2009]. Here 
Thus, a fourth goal of this workshop is to develop the concept of evolutionary games as ‘learning’ processes in which information is gained over time.
We shall try to synthesize this with Carl Bergstrom and Matina Donaldson-Matasci’s work on the ‘fitness value of information’: a measure of how much increase in fitness a population can obtain per bit of extra information [BL2004, DBL2010, DM2013]. Following Harper, we shall consider not only relative Shannon entropy, but also relative Rényi entropy, as a measure of information gain [Harper2011].
A fifth and final goal of this workshop is to study the interplay between information theory and the thermodynamics of individual cells and organelles.
Susanne Still has studied the thermodynamics of prediction in biological systems [BCSS2012]. And in a celebrated related piece of work, Jeremy England used thermodynamic arguments to a derive a lower bound for the amount of entropy generated during a process of self-replication of a bacterial cell [England2013]. Interestingly, he showed that E. coli comes within a factor of 3 of this lower bound.
In short, information theory and entropy methods are becoming powerful tools in biology, from the level of individual cells, to whole ecosystems, to experimental design, model-building, and the measurement of biodiversity. The time is ripe for an investigative workshop that brings together experts from different fields and lets them share insights and methods and begin to tackle some of the big remaining questions.
Bibliography
[AOE2008] D. Alonso, A. Ostling and R. Etienne, The assumption of symmetry and species abundance distributions, Ecology Letters 11 (2008), 93–105.
[TMMABB2012} D. Amodei, W. Bialek, M. J. Berry II, O. Marre, T. Mora, and G. Tkacik, The simplest maximum entropy model for collective behavior in a neural network, arXiv:1207.6319 (2012).
[B2011] J. Baez, Rényi entropy and free energy, arXiv:1102.2098 (2011).
[BFL2011] J. Baez, T. Fritz and T. Leinster, A characterization of entropy in terms of information loss, Entropy 13 (2011), 1945–1957.
[B2011] J. Baez and M. Stay, Algorithmic thermodynamics, Math. Struct. Comp. Sci. 22 (2012), 771–787.
[BCSS2012] A. J. Bell, G. E. Crooks, S. Still and D. A Sivak, The thermodynamics of prediction, Phys. Rev. Lett. 109 (2012), 120604.
[BL2004] C. T. Bergstrom and M. Lachmann, Shannon information and biological fitness, in IEEE Information Theory Workshop 2004, IEEE, 2004, pp. 50-54.
[BBS] M. J. Berry II, W. Bialek and E. Schneidman, An information theoretic approach to the functional classification of neurons, in Advances in Neural Information Processing Systems 15, MIT Press, 2005.
[BNS2001] W. Bialek, I. Nemenman and N. Tishby, Predictability, complexity and learning, Neural Computation 13 (2001), 2409–2463.
[BNS2002] W. Bialek, I. Nemenman and F. Shafee, Entropy and inference, revisited, in Advances in Neural Information Processing Systems 14, MIT Press, 2002.
[CL2012] C. Cobbold and T. Leinster, Measuring diversity: the importance of species similarity, Ecology 93 (2012), 477–489.
[CES2010] J. P. Crutchfield, S. Still and C. Ellison, Optimal causal inference: estimating stored information and approximating causal architecture, Chaos 20 (2010), 037111.
[D2004] R. C. Dewar, Maximum entropy production and non-equilibrium statistical mechanics, in Non-Equilibrium Thermodynamics and Entropy Production: Life, Earth and Beyond, eds. A. Kleidon and R. Lorenz, Springer, New York, 2004, 41–55.
[DJZ2006] R. C. Dewar, D. Juretíc, P. Zupanovíc, The functional design of the rotary enzyme ATP synthase is consistent with maximum entropy production, Chem. Phys. Lett. 430 (2006), 177–182.
[D2008] R. C. Dewar, A. Porté, Statistical mechanics unifies different ecological patterns, J. Theor. Bio. 251 (2008), 389–403.
[D2009] R. C. Dewar, Maximum entropy production as an inference algorithm that translates physical assumptions into macroscopic predictions: don’t shoot the messenger, Entropy 11 (2009), 931–944.
[D2010] R. C. Dewar, Maximum entropy production and plant optimization theories, Phil. Trans. Roy. Soc. B 365 (2010) 1429–1435.
[DBL2010} M. C. Donaldson-Matasci, C. T. Bergstrom, and
M. Lachmann, The fitness value of information, Oikos 119 (2010), 219-230.
[DM2013] M. C. Donaldson-Matasci, G. DeGrandi-Hoffman, and A. Dornhaus, Bigger is better: honey bee colonies as distributed information-gathering systems, Animal Behaviour 85 (2013), 585–592.
[England2013] J. L. England, Statistical physics of self-replication, J. Chem. Phys. 139 (2013), 121923.
[ODLSG2009} J. L. Green, J. K. Lake, J. P. O’Dwyer, A. Ostling and V. M. Savage, An integrative framework for stochastic, size-structured community assembly, PNAS 106 (2009), 6170–6175.
[Harper2009] M. Harper, Information geometry and evolutionary game theory, arXiv:0911.1383 (2009).
[Harper2011] M. Harper, Escort evolutionary game theory, Physica D 240 (2011), 1411–1415.
[Harte2008] J. Harte, T. Zillio, E. Conlisk and A. Smith, Maximum entropy and the state-variable approach to macroecology, Ecology 89 (2008), 2700–2711.
[Harte2009] J. Harte, A. Smith and D. Storch, Biodiversity scales from plots to biomes with a universal species-area curve, Ecology Letters 12 (2009), 789–797.
[Harte2011] J. Harte, Maximum Entropy and Ecology: A Theory of Abundance, Distribution, and Energetics, Oxford U. Press, Oxford, 2011.
[LH2013] M. Harper and C. Lee, Basic experiment planning via information metrics: the RoboMendel problem, arXiv:1210.4808 (2012).
[O2005] A. Ostling, Neutral theory tested by birds, Nature 436 (2005), 635.
[O2012] A. Ostling, Do fitness-equalizing tradeoffs lead to neutral communities?, Theoretical Ecology 5 (2012), 181–194.
[PS2012] D. Precup and S. Still, An information-theoretic approach to curiosity-driven reinforcement learning, Theory in Biosciences 131 (2012), 139–148.
Azimuth 
This sounds like a great meeting. We also explored the usefulness of the entropy concept to understand the physiological role of a certain class of enzymes in this paper. Basically, we hypothesized that increased entropy within a metabolic subsystem confers robustness to perturbations and fluctuations in the input to this system. However, at that point I was not aware of the connections between Gibbs’ approach to statistical mechanics/thermodynamics and Shannon’s theory as expounded by Jaynes. Since then I had time to explore this connection and luckily Jaynes has cleared up a lot of mysteries for me and, along the way, converted me to an objective Bayesian. I hope to apply these inferential concepts in the near future. Good luck with the conference.
Önder Kartal wrote:
Alas, it’s hard for me to understand this paper because I don’t know enough chemistry. It probably touches on some general issues that could be interesting even to a person like me who doesn’t know what’s a CAzyme, a glycan, or an α-1,4 glucosidic bond. But it’s hard for me to find those general issues, because I’m crushed by the terminology.
So, here’s a simple question. What’s a ‘polydisperse’ mixture of compounds?
I get the vague impression you’re trying to understand the nonequilibrium statistical mechanics of mixtures consisting of too many different compounds to list and treat individually. That’s an interesting challenge!
John Baez wrote:
To make it short: A mixture of similar compounds is called polydisperse with respect to some property, if the mixture contains compounds that differ by that property.
Consider a
-mer, that is a molecule where some chemical unit (e.g. glucose) is repeated 
times or has degree of polymerization 
. If these units are linked by the same type of chemical bond and the 3-dimensional conformation of the molecule is irrelevant, the number of bonds,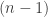 
, is a proxy for the energy. If I start with a system that has only say 3-mers, this is a monodisperse ‘mixture’. Now, there are enzymes that catalyze the dispersal of the energy in such systems without changing the energy content. How that? Well, they simply transfer monomer units between molecules by breaking a bond and building a bond. That is, while the number of bonds is a conserved quantity the energy becomes more and more spread out until the system reaches a Boltzmann distribution as the state of maximum entropy (see Box1 in the paper for further details). That’s why we speak of entropy-driven biochemical systems, since energy changes do not contribute to the motion of the system. A side note: You would get an inverted distribution if there would be an intrinsic upper limit to the degree of polymerization akin to systems with negative temperature; but that does not seem to be the case in reality so the potential maximum 
-mer length is unlimited.
In the open case with different enzymes acting, you have a system of enormous diversity and combinatorial complexity with new compounds generated all the time. This is tedious to describe by classical differential equations and if you choose an arbitrary finite upper limit to the length, you will probably get artifacts due to this choice. Hence our stochastic approach where new compounds are generated dynamically.
Cheers
Thanks! That was helpful. This is a really interesting new twist on statistical mechanics.
A fascinating workshop. Do you have any examples of the dangerous-sounding “conceptual pitfalls for the unwary”?
Karl Friston was mentioned on the comments here last year, but have you seen his recent work like this paper from Entropy which tries to apply the “free energy principle” to general biological systems?
My understanding of his argument is something like this: living systems need to remain within homoeostatic bounds to survive, so low entropy of their sensory states can act as an proxy for long-term adaptive fitness. Unlike adaptive fitness itself, it is observable and accessible to the system to guide it’s actions.
To minimize this entropy, it turns out that the controlling system has to model relevant aspects of the environment. But since the agent can’t directly observe these latent factors, it must make inferences about them in order to act. This inference involves a trade-off between maximizing the likelihood of sensory states (negative log likelihood, “Gibbs energy”), and maximizing the entropy of your beliefs about their latent causes in the environment. So you have an optimization problem with variational free energy, “energy” minus entropy, as the objective function. Friston goes on to argue that the optimal action to take is also given by minimizing this same objective function.
He makes this principle go a long way in describing computation in the brain, even using it to make concrete predictions about cortical structure. Yet it’s all based on the idea that living systems have to minimize their local Shannon entropy of their environmental states in order to survive. I’d like to understand better whether this quantity can be well defined, and whether it can really be a useful proxy for evolutionary fitness.
Ben wrote:
Well, for starters, despite the term ‘thermodynamics‘ the conceptually clearest part of the subject is the part based on equilibrium statistical mechanics… but living systems are inherently out of equilibrium. So we can’t blindly go ahead and use the marvelously powerful idea that a system in equilibrium maximizes its entropy subject to whatever constraints without some justification! Obviously there must be an important concept of ‘approximate equilibrium’ that approximately justifies it. But clarifying this concept is not easy.
And there are plenty of situations that are far from equilibrium, where what we’d really like is some new principles to guide us. Two principles I often see proposed are the principle of maximum entropy production and the principle of minimum entropy production. But that makes me very suspicious!
Occasionally I hear people offering to reconcile these seemingly contradictory principles, by saying when one holds and when the other holds. But I’ve never seen an explanation I really understand. (Of course, this could be my fault.) And when I’m walking down the road, I seem to be neither minimizing entropy production (I’m metabolizing faster than if I were just sitting there), nor maximizing it (running would produce more).
Another problem concerns the relation between information and entropy. I think I understand it, but I think some people don’t, and they can get confused.
Sounds like a great workshop!
Nonrendering mathematics in post:
Thanks—fixed! The usual thing: this WordPress blog requires math mode to start with
$latex
Professor Baez,
Will this help us understand what kind of new monster life forms will evolve in the ocean areas that are now sinking an otherwise enormous heat load to surface temperatures of the planet?
I don’t know. It should help us understand biology and ecology in useful ways. For example, Harte’s work may help us understand the change in biodiversity due to habitat loss, or global warming.
I applied, with no significant results, some time ago the Kullback-Leibler distance to try to replace the Smith-Waterman algoritm to DNA sequencing: all the theory that improve the sequencing to be useful to the treatment of genetic diseases.
The idea is to consider the alignment of the DNA string like a transmission channel of the input DNA across a black-box in an other sequence (with noise: change of bases and shifts); the relative entropy permit to measure the alignment between two DNA strings using a number of changes in the output string to minimize the distance.
The probability are rational number, so that the distance can be evaluated quickly as (a table of) logarithm of integers.
It is like a quaternary-digit Turing machine, and the noise can be a function, and the function can be a common deformation of the DNA string.
Prof Paltridge is retired, but still going strong in his contrarian way. You might consider inviting him.
That doesn’t smell right (for this astrobiology interested layman). Or at least, such a thing may be problematic.
What I know diversity in biology is still up in the air, and a recent paper claim that diversity is observed to vary randomly after mass extinctions:
“The survivors of the mass extinction, or the world they inherited, is so different from what went before that the rate of evolution is permanently changed.”
[ http://news.uchicago.edu/article/2012/07/02/mass-extinctions-reset-long-term-pace-evolution ]
This has to be one of the most exciting announcements I’ve heard all year! There is certainly a small, but quickly growing number of researchers focusing on the intersection of information theory and biology. I’ll put my name in to be the first person to register once things become firm. I’m also happy to help volunteer any time, talent, or expertise you might like to accept from me in terms of helping to organize/publicize this event. I’m an independent researcher based in Los Angeles and would be happy to travel out to you to discuss things in person if it’s convenient.
I do have a major caveat which you may wish to take into careful consideration as you proceed on this subject in particular regards to timing. At the beginning of 2013, the Banff International Research Station announced a closely related meeting on nearly the exact same (or certainly very closely related) topic: “Biological and Bio-Inspired Information Theory”.
I have to suspect that due to the relatively small number of researchers consciously working in the overlap of these two areas, that you consider contacting the BIRS group and possibly push your dates (theirs are Oct 26-31, 2014). If your dates aren’t firm, being able to move them by several months may help to further congeal this growing group of researchers rather than forcing a larger number of them decide between travel to two separate locations within the same week.
If it’s not possible to move dates, I’m going to have a nirvana week of vacation in late October next year!
I’ll also mention that I maintain a growing number of journal articles and references with relation to information theory and biology on the free Mendeley service which you may find useful: http://www.mendeley.com/groups/2545131/itbio-information-theory-microbiology-evolution-and-complexity/
Again, I’m at your service for any assistance this endeavor may require.
Thanks for pointing out that related conference! I’m reluctant to shift the time of ours, because most of the speakers of ours have already agreed to come at this time. There’s surprisingly little overlap with the BIRS conference, perhaps because people interested in ‘entropy’ are different than those interested in ‘information theory’, even though I think of them as two sides of the same subject. The one overlap I see is William Bialek, who wasn’t sure he could attend our conference. Anyway, I’ll think about it.
Thanks for your offer of help. I think the NIMBioS staff should do anything I can’t do… but I’ll see.
I’ll check out your list of references. How did you get interested in information theory and biology, and what aspect interests you most?
Maximum entropy production would predict global warming: A fast way to produce entropy is to burn things, which is basically what we are doing.
A counter example to maximum entropy might seem to be animals like penguins, which use all kind of ways to not loose heat. But on the other hand, if they didn’t do that, they would die, and then not be able to eat fish anymore. (ie. burn fish).. Looking at that example, it would seem that there is short term and long term maximisation. In the short term, you should burn all your food quickly, But in the long term, you may want to save some so that you and your offspring can continue to burn more food in the future. Perhaps global warming is such an example: It seems profitable in the short term, but perhaps not in the long term.
Does planet earth with life on it produce more entropy than earth without life? I guess that visible light photons from the sun should be absorbed, and turned into lower energy forms like heat. That is one of the things life does. But painting the earth black would perhaps be more efficient.
Gerard
John Baez has announced an upcoming three day workshop on “Entropy and Information in Biological Systems” to be hosted by the National Institute for Mathematical and Biological Synthesis […]
Very exciting stuff! As a student working on applications of information theory to transcription factor dynamics, this looks like to me like a really interesting set of questions and aims.
Glad to see maximum entropy production alive and well, it’s a fun idea. Even just its units are intriguing — length times thermal conductivity, or bits per second. Fascinating to think about systems that evolve to maximize these.
Professor Baez, for me “entropy” is a technical word whose conceptual meaning is supported by the context of physics. Then is one idea for the workshop that the context which makes “entropy” meaningful be expanded to also include biology as well as physics?
Going the other way around would be taking a technical word from biology and expanding the context which supports its conceptual meaning to include physics. But there might be a problem like “anthropomorphism”– attributing human characteristics to something other than a human. (For example everybody knows that one shouldn’t anthropomorphize computers because they get very angry about it!!)
I wonder if Max Tegmark’s “mathematical universe” would allow some useful exploration of anthropomorphizing- for every mathematical model of a universe, there is within the multiverse a universe exactly like it. (Wild!) Maybe such a technique would be like negative probability. Using it in the calculations but removing it in the answer. I can think of one possible example: probability learning.
From what I’ve read, humans, rats, and other animals from far back in the evolutionary trail all have the capability to “learn probabilities” (I’ve often wondered if something similar applies to roots and branches in the plant kingdom or the architecture of neurons in the brain. Schools of fish where each is a probability learner seem to attain a Nash equilibrium in certain experimental set-ups, but it’s too much to write about here.)
To demonstrate probability learning in the laboratory, the animal is presented with a number of possible spots to forage for food. For each foraging trip the experimenter establishes beforehand a probability for each possible spot that food will be supplied there. If the food is not provided at the spot the animal visits on a foraging trip, the food will be supplied at a different one and the animal is given that information about it’s having chosen the wrong possibility, thus missing out on some food. What happens in the experiment is that the animal learns the probabilities for food assigned by the experimenter to each spot and forages at each spot with the same probability as those determined beforehand by the experimenter.
To anthropomorphize, for each possible location of food I would assign to the animal two memory storages– (1) storage for the regret from remembered surprise at choosing a location in which case the food occurs somewhere other than that chosen location, and (2) storage for the regret from rememberd surprise at Not choosing this location when the animal has chosen a different possibility, but in which case the food does indeed occur at the location in question. So for each possibile location of food there is (a) regret at having chosen this possibility when the food occured at some different possibility, as well as (b) regret for having chosen some other possibility when the food occurred at the possibility in question.
Let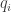
be the probability that food occurs at the 
th possibility during a foraging trip and 
be the probability that the animal will forage at that possibile location. Using these variables, here are the findings of the experiments: for each location of food 
, 
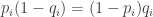with solution 
.
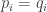In terms of surprisal, which perhaps implies something about entropy here, the situation of trying to forage at location
when the food appears somewhere else occurs with probability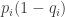 
. Because of this probability the animal experiences surprisal for this situation in the amount 
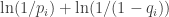. The associated regret for this situation is then like a force pushing the animal away from the location.
For the situation of trying to forage elsewhere, but then the food does indeed appear at location
, the probability is 
. Because of this probability the animal experiences surprisal in this situation in the amount of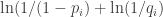 
. The associated regret for this situation is then like a force pushing the animal toward this location.
By means of the solution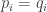
the animal evidently learns to make (a) the surprise and associated regret of choosing each location 
equal and opposite to (b) the surprise and associated regret of Not choosing each location 
:
These opposite kinds of regret then work like forces both attracting and repelling the animal toward each possible location during subsequent foraging episodes. For each possibility, the animal balances these two opposing “forces.” Here I’m using the words “regret” and “surprise” where perhaps “entropy” could be introduced, however without the benefit of anthropomorphizing.
Could one anthropomorphize physics by saying the Born rule is probability learning? For each possibility the Born rule assigns a possibility and a probability,
, where 
is real and 
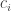is complex, modeling possibility. Substituting into the above equation for probability learning, one writes 
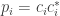(instead of 
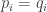), which is the Born rule of physics.
But where do the memories of surprise exist which create these two opposing “forces” of attraction and repulsion that are balanced for each possibility? They don’t exist in our universe. Applying Max Tegmark’s loophole, perhaps these memories would exist in another universe. One that’s coupled by the Born rule to our observeable universe.
There might be some rationale. Actual probabilities in our universe must be finite rational numbers, because they are determined by finite situations in a finite universe. But in the Born rule, the complex numbers associated with possibilities are continuous (at least in the Schordinger picture, where the Born rule is an equation). These continuous numbers in the Born rule would according to the loophole have to mean that the probabilities in the Born rule are determined by infinite situations. But infinite situations do not exist in our universe. However, following Tegmark’s idea, these infinite situations may exist in a different universe– an infinite universe coupled to our own by the Born rule.
There may be a benefit to producing this kind of mathematical model. If one starts with entropy and then tries to enlarge the supporting situation from physics to biology in order to model the opposing “forces” of regret in probability learning, the evolution from inanimate to animate should probably somewhere along the way be explained. But going the other way around, that is, starting with regret and then enlarging the supporting situation to possibly involve entropy, as above, means these memories of the two kinds of surprise for each foraging possibility have to be stored somewhere other than in our universe. Tegmark’s idea may suggest a place to hold them. And in this case it seems everything is animate! Thus removing the problem of having to explain animate from inanimate. Admittedly this comes at the heavy expense of coupling an infinite universe to our own by invoking Tegmark’s mathematical universe and the Born rule.
Could this kind of approach reveal some useful mathematics?
Lee wrote:
I’ll have to wait until I have more free time to read your whole post, but here is my reaction to this sentence. To me entropy is a technical word whose meaning is supported by the context of probability theory. If we have a probability distribution
its Shannon entropy is
and then there are lots of theorems that explain why this is a useful and important concept. There are also generalizations involving integrals instead of sums, generalizations like Rényi entropy, generalizations involving density matrices instead of probability distributions, etc.
Physics fits into this because in classical statistical mechanics, all we know is a probability distribution on the set of states of the system. The theorems I’m alluding to then give the laws of thermodynamics. (There’s a similar story for quantum statistical mechanics, using density matrices instead of probability distributions.)
But the usefulness of entropy is not limited to probability distributions that come from problems that are traditionally considered ‘physics’. Probability theory shows up all over!
Okay, I’ve read your comments a bit more. I think Max Tegmark’s mathematical universe hypothesis and the Born rule in quantum mechanics are pretty much irrelevant the more bio-relevant part of your comment, so I’ll ignore those. I don’t think talking about them helps here.
I like the idea that animals’ behavior approaching some ‘optimal’ behavior can be seen as a response to some ‘force’. We can try this analogy pretty much whenever we have a maximum principle or minimum principle available. If a system acts like it’s seeking to minimize some function
, then it acts like it’s feeling a force 
. If 
is related to entropy, then this force could be in part an entropic force.
However, there are lots of interesting problems with this idea. Are we claiming a specific law of motion for the system, like Newton’s law
or the gradient flow law (Aristotle’s law)
If so, we need some experiments and/or argument to justify this law. If not, what are we actually claiming?
Evolutionary game theory is a nice subject where people have tried out different laws of motion, some of which are related to information and entropy. So, that might be a place where people should start doing experimental tests of their ideas.
John wrote:
“…what are we actually claiming?”
In this area of research, no one has yet applied the mathematics of entropic force.
Research on the mathematics of probability learning seemed to be mature in William K. Estes’s review of 1972 (Research and Theory on the Learning of Probabilities, Author: William K. Estes, Source: Journal of the American Statistical Association, Vol. 67, No. 337 (Mar., 1972), pp. 81- 102).
But in fact, judging by the references now cited as basic for probability learning in a recent paper for the next “Handbook of Experimental Economics” (Learning and the Economics of Small Decisions, Ido Erev and Ernan Haruvy, 1 Technion and University of Texas at Dallas, To appear in the second volume of “The Handbook of Experimental Economics” edited by John H. Kagel and Alvin E. Roth.
August, 2013) the basic mathematical models for probability learning date from 1950. (Estes, W. K. (1950). Toward a statistical theory of learning. Psychological Review, 57, 94-107).
In those days, Jaynes’ MaxEnt reasoning (Jaynes, E. T., 1957, `Information Theory and Statistical Mechanics,’ Phys. Rev., 106, 620;) was not available in the mathematics of statistics that Estes used to model probability learning.
Further, Noam Chomksy’s famous 1959 criticsm of Skinner’s book, Verbal Behavior, was years away from becoming main stream psychology. 1959 was just the beginning of cognitive psychology, whose community is now huge compared to the behaviorist psychology of Skinner. So for example, to create a mathematical model as I did in the post which posits two memory stores for remembered surprise and regret would have been outlawed by the behaviorist paradigm. From the Wiki on Behaviorism: “The primary tenet of behaviorism, as expressed in the writings of John B. Watson, B. F. Skinner, and others, is that psychology should concern itself with the observable behavior of people and animals, not with unobservable events that take place in their minds. ref: (Skinner, B.F. (16 April 1984). “The operational analysis of psychological terms”. Behavioral and Brain Sciences 7 (4): 547–81).
Moreover the concept of regret did not dramatically play a role in decision psychology until 1979, when Daniel Kahneman and Amos Tversky introduced it in a lecture and then published the paper in 1982. (Kahneman, Daniel; Tversky, Amos (1982). “The simulation heuristic”. In Daniel Kahneman, Paul Slovic, Amos Tversky. Judgment under uncertainty: heuristics and biases. Cambridge: Cambridge University Press).
Nor can I find the Shannon-theoretic definition of “Surprisal” (as in the formula posted) in the above review for The Handbook of Experimental Economics. They use their own definition of surprise, which appears to be different.
So John when you write, “Are we claiming a specific law of motion for the system, like Newton’s law or the gradient flow law (Aristotle’s law?” Yes, the equation that models an equilibrium between two different kinds of surprisal does seem law-like. It seems more basic to me than any of the mathematical models I see in Estes’ work, or in the above review. But how could they have known? Although I’m just a fan (and therefore everybody is free to ignore my statements with absolutely no risk of offending me), until you told me about it I too was ignorant of entropic force.
Maybe with some math building on what you’ve pointed me to, one could predict that future experiments of an appropriate type will reveal a new mechanism for evolution.
First I would have to say a bit about Chapter 11 “Rate” in The Organization of Learning (C. R. Gallistel, 1990, MIT Press).
In the previous post the subject in the experiment was supplied with the information that when it chose a possibility and the food occurred at a different possibility, this was the situation. In his book Professor Gallistel tells how he has a class of undergraduates compete against a lab rat to see who gets the most food. The undergraduates are given the above information but the rat is not. Professor Gallistel does not tell them this. The students in his classroom match probabilities but the rat does not, because the information of its having missed out on food at a different possibility is hidden from it. So after a short while the rat just always forages at the channel with the highest probability for food being there.
Say that the experimenter establishes beforehand that the probability for the food occurring at one channel is 0.7. While the probability for food occurring at the other channel is 0.3. The students in the classroom match probabilities, so for a hundred servings of food each student gets total food of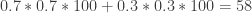
.
But lacking the same information on which to base regret, and so freezing on the highest payoff channel, the rat gets total food of
Thus proving to the undergraduates that a rat has outperformed them in what they very probably see as some kind of intelligence test!
At this point Professor Gallistel shows that information was hidden from the rat. And if the rat has the same information, it scores the same as the undergraduates.
Next in the chapter, Professor Gallistel relates experiments with a group of ducks and experiments with a group of fish that show for two different channels of receiving food, when foraging the animals divide themselves into two groups, the number of individuals at each of the two channels in proportion to the rate of food delivered there.
So, for example, if the rate for one channel is 0.7 and the rate for the other channel is 0.3, then out of (say) 10 individuals, 7 will station themselves at the former channel and 3 will station themselves at the latter channel. If all of the individuals were performing probability learning as in the first experiment described, then that same number would on the average be appearing at each channel.
However in this experiment something different happens. The individuals no longer travel to one channel and then to the other, as each would in an individual probability learning experiment. Rather, the number of trips each individual makes between channels is drastically reduced. This looks like a Nash equilibrium, because at the channel with the rate of 0.7 for food appearance the rate for each individual stationed there is
per individual. While at the other channel the rate for each individual is 
per individual.
And no individual can improve this payoff just by changing its own strategy. If one individual goes to the other channel, then for example the payoff per individual at the abandoned channel would be
per individual while payoff at the newly adopted channel would be 
per individual. One individual changing its channel like this would reduce its payoff from 10 to 7.5. It looks like a Nash equilibrium.
From the first experiment we know that hiding information results in the rat freezing at the highest payoff channel. Similarly, how could information be hidden in the group situation to hold individuals at a channel for some period of time? In certain circumstances fear might cause an individual to ignore information. For example, the group of individuals over there at the other food channel might look like just one big unit– significantly bigger than the individual observing it. So if one individual fears another because of bigger size, then that might be a reason to ignore the information that food is over there, because who wants to get attacked by a big unit who is much bigger than you? Probably need to explain this better, but I leave the details for later.
Finally, if the fish in this experiment are like dollar bills in a capital budgeting process, then this is a model of optimal captial budgeting.
It also looks like a mechanism for evolution.
Certain critics of whom we are all aware use the concept “irreducible complexity.” Frankly I’ve never listened to them, but I think I can imagine what that criticism might be. I’ll use an automobile for an example in order to reduce my chances of getting the biology wrong.
A car is a system with components like engine, transmission, drive shaft, frame, body, brakes, etc. etc. Say that each component is the result of variation and selection, as usual. Now we have a problem.
Say that we have a fabrication site where all the components are assembled into the final system. Then it’s the system that performs in the environment and gets payoffs in that environment. In variation and selection as usual, the reduced payoff means that kind of system will not get enough food or energy to reproduce, and so its kind will soon die off, being de-selected.
However, in this example the system was fabricated and does not reproduce itself. Only the components reproduce themselves. If we invent some way by which the payoff from the system is passed onto the components, then we could get situations like the following. Cars where almost every component is perfect save one (say, the brakes) are de-selected by the environment. But if that de-selecting payoff is handed off to each component, then every perfect component in the car will in this case de-selected. Even perfection is not enough to get a component selected.
Now the previously perfect components are being degraded. And sooner or later one of them will get the system de-selected. In that case, no matter what improvements have happened in the brakes, they will also be de-selected because of the other components the previously very imperfect brakes have caused to be de-selected. Instead of improving, the brakes will get worse until once again they get the system de-selected. In which case, no matter what improvements the other components have made, they will be de-selected, degrading them. And so on.
Maybe there are other problem statements for “irreducible complexity” but I will leave it at this. Next: a new mechanism for evolution.
First I would need apoptosis– programmed death of components or systems. Anything that’s imperfect, whether compononent or fabrication site attracting components, gets destroyed by apoptosis.
Next I would need a genetic variation of components that are attracted to the fabrication site in which the Nash equilibrium occurs. The needed genetic variation must produce mutually attaching components which, when involved in the Nash equilibrium, after some amount of time attach themselves to each other.
Finally, I would need a genetic variation of the fabrication site in order to explore different ways of attracting these components.
This is just a rough draft, of course. Hoping to make it a final draft at some later time, I must add a final note in my fan letter.
Fear, regret, and surprise are familiar terms to those of us who anthropomorphize. But for the above mechanism of evolution to work, the only thing (as a fan) that I can think of is genetic variation for fabrication sites which produces self-rewriting Hamiltonians, or in another domain, self-redrawing Petri nets that are just as powerful as Turing machines. To remember surprise, the Hamiltonian re-writes itself to an appropriate, slightly different Hamiltonian. To ignore information, the Hamiltonian re-writes itself to an appropriate, slightly different Hamiltonian.
The killing machines of Apoptosis and the deadly game that gives them birth.
The story begins a long time ago– in PetriNetTown, the first village in the history of fabrication hives.
Death squads of roboticPetriNets roamed the paths of the village, killing all who violated the laws. They enforced the Esslaws of the death arena, at which the citizens would gather in great numbers, rewarding the winner, and best of all making sure that losers died without doubt, in fact scavenging their remains for food that could be fed back to the ever-hungry fabrication nests.
The rules are thermodynamic. According to the law, each hive may fabricate killer RoboticPetriNets (kRPN) only in strength proportional to the fabricating capability of the hive itself. In terms of the canonical fabricated system, the hive fabricating at a rate of 10 is allowed by law to fabricate kRPNs of greater capability for killing than hives fabricating at a rate of 5.
In fact, the law holds that kRPNs fabricated from hives of rate 10 can kill systems only from hives of rate lower than 10. An kRPN fabricated by a hive of one rate can never kill systems fabricated by any higher rate hives; and may only kill systems fabricated by lower rate hives.
Without a doubt the most valuable systems fabricated by the hives are those which forage for each hive and bring it back food. Unfortunately they become easy prey for the kRPN fabricated by every higher rate hive in the arena.
Sooner or later at the amusement of the crowd, lower rate hives in the arena die and their parts are scavenged, victim of the kRPN from all higher rate hives in the arena.
At the end of the game only the highest rate hive remains– one alone, victorious in the arena. Best of all, only its kRPN survive. The others are dead, with their parts fed back to the ever-hungry fabrication hive.
It’s a stable strategy. Say that the one remaining fabrication hive makes a mistake in fabricating a system, thereby fabricating a defective system.
The laws of thermodynamics make it so that these defective systems can only perform as well as could a system fabricated by a lower rate hive.
Thereby, defective fabricated systems serve as easy bait for the survivor kRPN. Defective systems are thus killed and their parts fed back to the ever-hungry fabrication hive.
The killing machines of Apoptosis– yet another gruesome story from thermodynamics!
https://docs.google.com/file/d/0B9LMgeIAqlIESll2YXdQZTB1NVE/edit?usp=docslist_api
Here’s a Petri net diagram of the Probability Learning Game
Whether entropy production is minimized, maximized, or neither depends on the boundary conditions of the system. As a rule of thumb, if a system is effort constrained, entropy production is maximized, while if it’s flow constrained, entropy production is minimized, e.g.
Minimum energy dissipation model for river basin geometry.
This reminds me of the post about the Anasazi and the phase transition between the dominance of powerful and efficient cultures that occurs when environmental constraints change. The near future looks likely to be a time when a transition from being powerful to being efficient would be in humanity’s best interest. The important questions would then be: which artificial constraints should be imposed in order to hasten this transition and reduce the amount of suffering it will entail? Is pre-adaptation to an anticipated future environment possible? Without understanding entropy and information in biological systems, the effects of some efforts may even be opposite to their intent.
David wrote:
One of my goals is to reconcile Prigogine’s ‘principle of minimum entropy production’ with Dewar’s ‘principle of maximum entropy production’, or else throw out the latter completely (since I understand some contexts where the first one is true). Here are my feeble attempts so far:
• Extremal principles in non-equilibrium thermodynamics, Azimuth Wiki.
Your remark gave me hope, but then dashed it. ‘Effort’ is a generalization of voltage to general systems, while ‘flow’ is a generalization of current. I asked myself:
Is your remark make sense for electrical circuits made only of resistors? If I can’t understand entropy minimization versus entropy maximization even in that case, that’s pretty bad.
If we fix the voltage at the terminals, I know the other voltages are chosen to minimize power, which is the rate of entropy production. So, in this case, entropy production is minimized when we constrain the effort at the terminals.
But that’s the opposite of your rule of thumb!
For various reasons we have decided to reschedule our workshop
to Wednesday-Friday, April 8-10, 2015.
One reason is that on October 26-31, 2014 there will be a workshop on Biological and Bio-Inspired Information Theory at the Banff International Research Station.
Another is that hotels in Knoxville tend to be booked for football games in the autumn!
And in April 2015, Marc Harper and I are helping run a workshop on entropy and information in biological systems! We’re doing this with John Harte […]
I’ve just noticed another upcoming workshop similar to this – which might be mined for additional presentations and/or potential participants: “Entropy in Biomolecular Systems” hosted by CECAM from May 14 to 17, 2014, in Vienna.
It’s really excellent to see this very specific area of research seeing so much attention!
Thanks for the notification! I’m hanging out in Erlangen this spring, so I could conceivably go to that meeting… except that I’ll be attending a meeting on computer science and category theory in Paris from May 10 to May 24!
However, it’s still good to find out names of more people working in this general area. It has so many aspects, it seems hard to located everyone who is interested.
John Harte, Marc Harper and I are running a workshop! Now you can apply here to attend:
• Information and entropy in biological systems, National Institute for Mathematical and Biological Synthesis, Knoxville Tennesee, Wednesday-Friday, 8-10 April 2015.
Click the link, read the stuff and scroll down to “CLICK HERE” to apply. The deadline is 12 November 2014.
Exciting all this activity on information and bio-sciences. Most likely I won’t finished anything meaningful on time, but I hope knowing of it helps me make up my mind into dropping it or giving it a final push.
Laments aside, here a minuscule glitch on your text, John: The first reference has an incorrect link. Alonso’s paper referred there can be downloaded from http://www-personal.umich.edu/~aostling/papers/alonso2008.pdf
Good luck! Thanks for catching that glitch—it should be fixed now.
[…] John Baez has announced a workshop on Entropy & Information in Biological Systems https://johncarlosbaez.wordpress.com/2013/11/02/entropy-and-information-in-biological-systems/&… #NIMBioS #ITBio […]