The hypocycloid with n cusps is the curve traced out by a point on a circle rolling inside a circle whose radius is n times larger.
The hypocycloid with 2 cusps is sort of strange:
It’s just a line segment! It’s called the Tusi couple.
The hypocycloid with 3 cusps is called the deltoid, because it’s shaped like the Greek letter Δ:
The hypocycloid with 4 cusps is called the astroid, because it reminds people of a star:
I got interested in hypocycloids while writing some articles here:
My goal was to explain a paper John Huerta and I wrote about the truly amazing things that happen when you roll a ball on a ball 3 times as big. But I got into some interesting digressions.
While pondering hypocycloids in the ensuing discussion, the mathematician, physicist, programmer and science fiction author Greg Egan created this intriguing movie:

It’s a deltoid rolling inside an astroid. It fits in a perfectly snug way, with all three corners touching the astroid at all times!
Why does it work? It’s related to some things that physicists like: SU(3) and SU(4).
SU(n) is the group of n × n unitary matrices with determinant 1. Physicists like Pauli and Heisenberg got interested in SU(2) when they realized it describes the rotational symmetries of an electron. You need it to understand the spin of an electron. Later, Gell-Mann got interested in SU(3) because he thought it described the symmetries of quarks. He won a Nobel prize for predicting a new particle based on this theory, which was then discovered.
We now know that SU(3) does describe symmetries of quarks, but not in the way Gell-Mann thought. It turns out that quarks come in 3 ‘colors’—not real colors, but jokingly called red, green and blue. Similarly, electrons come in 2 different spin states, called up and down. Matrices in SU(3) can change the color of a quark, just as matrices in SU(2) can switch an electron’s spin from up to down, or some mix of up and down.
SU(4) would be important in physics if quarks came in 4 colors. In fact there’s a theory saying they do, with electrons and neutrinos being examples of quarks in their 4th color state! It’s called the Pati–Salam theory, and you can see an explanation here:
• John Baez and John Huerta, The algebra of grand unified theories.
It’s a lot of fun, because it unifies leptons (particles like electrons and neutrinos) and quarks. There’s even a chance that it’s true. But it’s not very popular these days, because it has some problems. It predicts that protons decay, which we haven’t seen happen yet.
Anyway, the math of SU(3) and SU(4) is perfectly well understood regardless of their applications to physics. And here’s the cool part:
If you take a matrix in SU(3) and add up its diagonal entries, you can get any number in the complex plane that lies inside a deltoid. If you take a matrix in SU(4) and add up its diagonal entries, you can get any number in the complex plane that lies inside an astroid. And using how SU(3) fits inside SU(4), you can show that a deltoid moves snugly inside an astroid!
The deltoid looks like it’s rolling, hence the title of this article. But Egan pointed out that it’s not truly ‘roll’ in the sense of mechanics—it slides a bit as it rolls.
For the details, see this article on my other blog:
• Deltoid rolling on an astroid.
But the really cool part—the new thing I want to show you today—is that this pattern continues!
For example, an astroid moves snugly inside a 5-pointed shape, thanks to how SU(4) sits inside SU(5). Here’s a movie of that, again made by Greg Egan:

In general, a hypocycloid with n cusps moves snugly inside a hypocycloid with n + 1 cusps. But this implies that you can have a hypocycloid with 2 cusps moves inside one with 3 cusps moving inside one with 4 cusps, etcetera! I’ve been wanting to see this for a while, but yesterday Egan created some movies showing this:

Depending on the details, you can get different patterns:

Egan explains:
In the first movie, every n-cusped hypocycloid moves inside the enclosing (n+1)-cusped hypocycloid at the same angular velocity and in the same direction, relative to the enclosing one … which is itself rotating, except for the very largest one. So the cumulative rotational velocity is highest for the line, lower for the deltoid, lower still for the astroid, in equal steps until you hit zero for the outermost hypocycloid.
In the second movie, the magnitude of the relative angular velocity is always the same between each hypocycloid and the one that encloses it, but the direction alternates as you go up each level.
Here’s one where he went up to a hypocycloid with 10 cusps:

Note how sometimes all the cusps meet!
Yonatan Zunger is the chief architect of Google+, but before that he used to work on string theory. Reading about this stuff on Google+, he had a number of interesting ideas, like this:
I wonder, can a deltoid roll in a 5-hypocycloid? I haven’t worked through the math of just how the SU(n) → SU(n+1) embedding guarantees a fit here.
(And also, are there corresponding pictures we could draw to illustrate the embeddings of other Lie groups? This could be a lovely way to illustrate a wide range of relationships if it could be done more generally.)
Egan figured out that yes, a deltoid can move nicely in a hypocycloid with 5 cusps:

He writes:
To make this, I took the border of a deltoid in “standard position” (as per the trace theorem) to be:
Suppose I apply the linear function:
to the whole deltoid. Then at the point s=t on the deltoid, we have:
which is a point on a 5-cusped hypocycloid in “standard position”. Of course with this choice of parameters you need to take
from
through to
not
to complete a cycle.
Using the same trick, you can get a hypocyloid with n cusps to move inside one with m cusps whenever n ≤ m. As for the more general question of how different Lie groups give different ‘generalized hypocycloids’, and how fitting one Lie group in another lets you roll one generalized hypocycloid in another, the current state of the art is here:
• N. Kaiser, Mean eigenvalues for simple, simply connected, compact Lie groups.
But there is still more left to do!
On a somewhat related note, check out this fractal obtained by rolling a circle inside a circle 4 times as big that’s rolling in a circle 4 times as big… and so on: astroidae ad infinitum!




Clockmakers and watchmakers used to make gear teeth using these patterns (or segments of their epicycloidal counterparts). Nowadays involute gears are prefered — they’re more tollerant of varying axle separation — but it’s easier to machine flat pinion leaves by hand, which works because a diameter line is part of a 2-cusp cycloid.
With more horological remarks
So here are few obvious questions that I don’t have time to think about right now. :-(
Is there actually an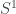 family of embeddings
family of embeddings 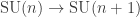 ?
?
And what about the Can we at least find similar relation between
Can we at least find similar relation between  and
and  ?
?
Regarding Zunger’s suggestion on trying out to illustrate embeddings of other Lie groups – the obvious suggestion is to use another symmetric polynomial in eigenvalues, say or
or  and look at
and look at 
Vit wrote:
Usually when we talk about embedding one group in another, we mean doing so via a homomorphism. There are lots of such embeddings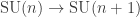 ; pick the obvious one and get more by conjugating it with elements of
; pick the obvious one and get more by conjugating it with elements of 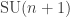 . I believe (but have not proved) that this trick gives all the embeddings.
. I believe (but have not proved) that this trick gives all the embeddings.
However, since the trace is invariant under conjugation, it’s not these embeddings that explain how the set rolls around in the set
rolls around in the set  , as you see here:
, as you see here:
<div align = "center"

The actual explanation can be on my Visual Insight blog. The eigenvalues of a matrix in are of the form
are of the form
where the angles are arbitrary. On the other hand, the eigenvalues of any element of
are arbitrary. On the other hand, the eigenvalues of any element of 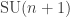 can be written as
can be written as
where the angles and
and  are arbitrary. Thus we have
are arbitrary. Thus we have
As ranges from
ranges from  to
to 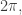 this gives a filled-in hypocycloid with
this gives a filled-in hypocycloid with  cusps rolling snugly inside one with
cusps rolling snugly inside one with 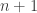 cusps!
cusps!
Perhaps a presentation that is a bit easier to understand is the maximal torii; since we’re only looking at compact groups, every element is conjugate to something in a maximal torus, and the trace is invariant under conjugation, so the image of the trace over the maximal torus is the image of the trace over SU(n). SU(n) has an (n-1)-dimensional maximal torus, and SU(n+1) has an n-dimensional maximal torus, and we can view the n-dimensional torus as the product of the (n-1)-dimensional torus and S^1. This has the helpful property of easily abandoning the group structure, so we don’t worry about the embeddings being homomorphisms or not.
Yes, this is a good way to think about it. Concretely one can think of the maximal torus of SU(n) as the set
and the trace map as the linear functional
that just sums all the components of a vector. We could study this sort of thing for other compact Lie groups, either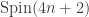 using the trace in the complex spinor representation, or more general Lie groups using other linear functionals! I haven’t had time to try it. But it seems this approach should give us various sets
using the trace in the complex spinor representation, or more general Lie groups using other linear functionals! I haven’t had time to try it. But it seems this approach should give us various sets
where the angles are constrained by linear relations, probably with integer coefficients. So the fun would be to understand the sets that arise.
are constrained by linear relations, probably with integer coefficients. So the fun would be to understand the sets that arise.
I think this is how it goes for the Spin(4n+2) case:
Viewing the maximal torus of Spin(4n+2) as diagonal matrices, we get the maximal torus of Spin(4n+6) by taking the Kronecker product with the diagonal matrix
So for in Spin(4n+2) and
in Spin(4n+2) and 
Unfortunately, is always real, wandering between 4 and -4, so we get squashing but no rotation or anything of the sort. In other words, the Spin(6) = SU(4) case gets us an astroid, and the embedding of that into Spin(10) gets us an astroid that grows and shrinks, but further Spins don’t get us any new behavior.
is always real, wandering between 4 and -4, so we get squashing but no rotation or anything of the sort. In other words, the Spin(6) = SU(4) case gets us an astroid, and the embedding of that into Spin(10) gets us an astroid that grows and shrinks, but further Spins don’t get us any new behavior.
I wonder if another useful way of thinking about this is as a group homomorphism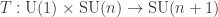 , where the image of
, where the image of  is the subgroup of
is the subgroup of  -block-diagonal matrices within
-block-diagonal matrices within 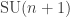 .
.
Explicitly,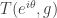 is the matrix whose
is the matrix whose 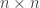 block is
block is  and whose
and whose  block is
block is  . You can then obtain all the group-homorphic embeddings of
. You can then obtain all the group-homorphic embeddings of  in
in 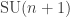 by conjugation, but they all look the same when we take the trace.
by conjugation, but they all look the same when we take the trace.
More generally, there’s a group homomorphism , where
, where  is an
is an  -block-diagonal matrix with the
-block-diagonal matrix with the  block given by
block given by  and the
and the  block given by
block given by 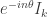 . (Putting
. (Putting  , and with a different parameter of
, and with a different parameter of  , that’s how I got the deltoid rolling in the 5-hypocycloid.)
, that’s how I got the deltoid rolling in the 5-hypocycloid.)
Ah, and we can also have a group homomorphism , where
, where 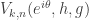 is an
is an  -block-diagonal matrix whose
-block-diagonal matrix whose 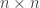 block is
block is  and whose
and whose  block is
block is 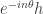 .
.
If you chose to fix different values of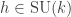 , you would get different ways of embedding an
, you would get different ways of embedding an  -hypocycloid moving inside an
-hypocycloid moving inside an  -hypocycloid, depending on
-hypocycloid, depending on  .
.
For example, this movie for shows
shows  :
:
Cool! And I think your homomorphism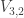 is the famous homomorphism
is the famous homomorphism
which is used to embed the Standard Model into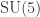 grand unified theory! I guess your movie actually illustrates that case!
grand unified theory! I guess your movie actually illustrates that case!
If you don’t remember this stuff, you can see it discussed here. Scroll down until you hit the big equation defining .
.
Since this homomorphism explains why quarks have the weird charges they do—if you believe in the
explains why quarks have the weird charges they do—if you believe in the 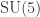 GUT—maybe some movies like the ones you’re making could illustrate some ideas from particle physics!
GUT—maybe some movies like the ones you’re making could illustrate some ideas from particle physics!
That explains my sense of déjà vu when I was writing this!
Here’s the best I can do so far at giving a physical interpretation of this movie:
In lattice gauge theory we chop spacetime into hypercubes and label each edge with an element of our gauge group. This describes the gauge field. The action in lattice gauge theory is a sum over all the square faces of our hypercubes. For each square we go around and multiply the group elements
of our gauge group. This describes the gauge field. The action in lattice gauge theory is a sum over all the square faces of our hypercubes. For each square we go around and multiply the group elements  labelling its edges. We take the product
labelling its edges. We take the product
This is the holonomy of the gauge field around the square. We then compute the Wilson loop function
in some representation, and then subtract this from its largest possible value (the dimension of that representation). That’s what we sum over squares! It’s zero when our gauge field is flat, that is, when the holonomy around each square is 1.
So now look at the case of the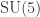 grand unified theory. There’s a homomorphism
grand unified theory. There’s a homomorphism
where the three factors correspond to the hypercharge force, the strong force and the weak force. (The hypercharge force and weak force combined are another way of thinking of the electroweak force.)
If we let the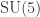 gauge field be arbitrary, the value of the Wilson loop function
gauge field be arbitrary, the value of the Wilson loop function
can be anything inside the 5-cusped hypocycloid here:
If we set the hypercharge and weak force gauge fields equal to zero, the Wilson loop function must lie inside some particular deltoid sitting in the 5-cusped hypocycloid. This is still true if the hypercharge force is set equal to any constant value—but then we get a different deltoid.
I hope that as we turn up the hypercharge force, the deltoid rolls around precisely as shown in this movie! I haven’t actually done the calculation: I’m posting a bit hastily here. To check, we should study the set of allowed values of
where is anything in
is anything in 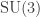 , while
, while 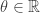 takes some fixed value. We’ll get a deltoid for any choice of
takes some fixed value. We’ll get a deltoid for any choice of  : I think that’s easy to see. I’m hoping it rolls nicely as we vary
: I think that’s easy to see. I’m hoping it rolls nicely as we vary 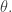
Yes, that’s exactly in accord with the formula I used for that movie of the rolling deltoid (apart from an irrelevant factor in the phase I used, which was chosen to describe the point of contact between the curves rather than anything more physical).
Great, this makes for a fun interpretation of the movie!
It would be nice if there were some use for this interpretation. In an attempt to blunder toward this, we could ask:
• What’s special about an element of whose trace lies at a cusp of a hypocycloid? I think I know the answer—it’s related to how the center of the group
whose trace lies at a cusp of a hypocycloid? I think I know the answer—it’s related to how the center of the group  is
is 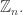 So this one counts as a puzzle rather than a research problem.
So this one counts as a puzzle rather than a research problem.
• What’s special about the values of that make a cusp of the deltoid land snugly in the cusp of the 5-cusped hypocycloid? In other words, what’s special about
that make a cusp of the deltoid land snugly in the cusp of the 5-cusped hypocycloid? In other words, what’s special about  such that for all elements
such that for all elements
the element
has a trace lying in a deltoid with cusp equal to one of the cusp of the 5-cusped hypocycloid
For the first puzzle: if an element of has n equal eigenvalues (which must be nth roots of unity), its trace will achieve the maximum possible absolute value of n, and lie on the disk that circumscribes the hypocycloid, which only the cusps intersect. And the only elements with equal eigenvalues like that are nth roots of unity times the identity, i.e. elements of the form
has n equal eigenvalues (which must be nth roots of unity), its trace will achieve the maximum possible absolute value of n, and lie on the disk that circumscribes the hypocycloid, which only the cusps intersect. And the only elements with equal eigenvalues like that are nth roots of unity times the identity, i.e. elements of the form  for
for 
But I don’t see how the second puzzle can have a solution. I don’t think a choice of alone can guarantee anything about
alone can guarantee anything about  . In the movie I made with three choices for h:
. In the movie I made with three choices for h:
one choice has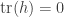 , and the cusps of the corresponding deltoid never touch the cusps of the 5-hypocycloid, for any value of
, and the cusps of the corresponding deltoid never touch the cusps of the 5-hypocycloid, for any value of  . And even for the two different choices of h with
. And even for the two different choices of h with 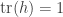 , the cusps of the deltoid coincide with the cusps of the 5-hypocycloid at different values of
, the cusps of the deltoid coincide with the cusps of the 5-hypocycloid at different values of  .
.
Okay, let me fix my second question! I should ask: what sets of choices of give values of the trace
give values of the trace  that range over a deltoid having a cusp that touches a cusp of the 5-epicycloid?
that range over a deltoid having a cusp that touches a cusp of the 5-epicycloid?
Oops, I should have said in my previous comment, not
in my previous comment, not 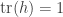 . That is, the movie has
. That is, the movie has  , and hence
, and hence 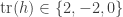 .
.
I need to get that straight to answer the revised second question! The deltoid has cusps where , and the 5-hypocycloid has cusps where
, and the 5-hypocycloid has cusps where 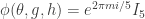 . So we need
. So we need 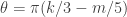 in order that the first three diagonal elements are correct, and then we need
in order that the first three diagonal elements are correct, and then we need 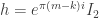 .
.
This implies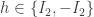 and
and  .
.
So I think the answer to the question is that you get a deltoid with one cusp coinciding with one of the 5-hypocycloid cusps by letting range over all of
range over all of 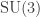 , while fixing
, while fixing 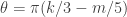 and
and 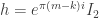 for any
for any 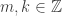 .
.
Bravo!
I think one can push the visualisations even a bit further, since is isomorphic to
is isomorphic to 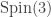 and hence any path of rotations could give us a nicely moving
and hence any path of rotations could give us a nicely moving  -hypocycloid inside of
-hypocycloid inside of  -hypocycloid via
-hypocycloid via
What would Dirac’s belt trick correspond to? :) One can also add Hopf fibration to better visualize
to better visualize  .
.
[…] Rolling Hypocycloids, par John Baez. […]
Another cool post, John. BTW, an n-cusped object rolling inside an n+1-cusped object is ubiquitous in the automotive world; it’s what’s called a trochoidal oil pump.
Interesting!
That led me to the Wikipedia articles on the gerotor:
Thanks Greg & John for creating and sharing these fascinating, beautiful patterns.
You’re welcome! Obviously Greg did most of the work.
In a way, something similar is used to drill square holes with drill bits shaped like Reuleaux triangles. Though not a hypocycloid, the Reuleaux triangle does maintain three points of contact with the outer square at all times and this could probably be extended to higher Reuleaux polygons.
Yes, there’s some resemblance between the deltoid inside the astroid:
and the Reuleaux triangle, which is a famous curve of constant width:
However, I don’t know any precise relation, except for the fact that they both have a small curve moving in a big one while keeping three points of contact, and that the small curve is not truly rolling: it’s slipping!
A while ago Greg noticed that the deltoid is slipping, as are all the higher hypocycloids in this and the other pictures here:
I’ve fixed this blog article to reflect that.
Can you guys create a rolling tetrahedral hypocycloid? Does it exist? Or how about a 3D hypocycloid with an internal 2D hypocycloid that looks like a line in a perpendicular view?
I can think of how to trace a Platonic polyhedron, with cusps at its vertices, and hypocycloids as edges, using a small ball inside a larger ball. But the small ball would only be allowed to trace out certain trajectories. I can’t see yet if you can trace out faces along with the edges.
Gerard
Fascinating discussion and movies! Of course the hypocycloid is a special case of the hypotrochoid. Another special case is the ellipse – produced by rolling a circle inside a circle. I have wondered if the inverse is possible, that a circle could be traced by rolling an ellipse inside an ellipse, but the math was beyond me to explore this question.
I’m seeing generalized Wankel engines in there somewhere, too
[…] Evelyn Lamb describes John Baez’s Rolling hypocycloids: […]
[…] from which I transferred: Rolling Hypocycloids The hypocycloid with n cusps is the curve traced out by a point on a circle rolling inside a […]
Did anybody notice this? Rolling a deltoid inside an astroid is just like rolling a circle of radius 3 inside a circle of radius 4. The contact point moves just like rolling a circle of radius 1 inside a circle of radius 4:
Same is true for rolling a deltoid inside a hypocycloid with 5 cusps:
Similarly, any hypocycloid can roll nicely on a cycloid. The contact point traces the cycloid in an standard way. Do you think it comes from a group embedding?
These are very nice, Ali! I think these two are implicit in work Egan has already done, but they’re still nice to see:
The ones involving a cycloid seem more surprising to me!
These are great!
I never thought about a hypocycloid rolling on a cycloid. In retrospect it’s a really simple idea: if you have a circle of radius 1 and a circle of radius n rolling on a line, with the x-coordinates of their centres staying the same, the small circle must be truly rolling inside the big one, because the linear velocities of points fixed to the perimeter of either circle are both zero at the point of contact.
A point fixed to the small circle as it rolls must trace out a cycloid in the plane, but in coordinates locked to the larger circle, the same point must trace out a hypocycloid … which in turn is rotating and advancing with the large circle.
A similar thing must be true for epicycloids, hypocycloids and the cycloid rolling on each other.
Yes, I was thinking the same. Here is a picture:
You and Greg should be able to make these pictures by just changing a couple of minus signs in the hypocycloid case.
Gerard
My picture is actually an epicycloid in an epicycloid, so not quite the same. I can think of cool variations, I’ll make some soon.
Gerard
More pictures:
(Click to enlarge.)
Thanks, these are nice!
(I turned your links into pictures visible here. When I do this, I usually make it so people can click on them and go to the original pictures, which are often larger.)
What is the precise mathematical description of what’s going on here?
Are the shapes rolling inside the hypocycloid a bunch of epicycloids?
To explain the maths behind the pictures:
If you look at the generating formula’s for the epicycloid and the hypocycloid, you can notice that they are in fact the same, if you allow negative numbers for the parameters. In the Wikipedia formula, fill in a negative ‘r’ to go from ‘epi’ to ‘hypo’.
If you take the pictures of Greg and Ali and and fill in a negative r, some interesting features continue to work. An n-cycloid fits in exactly in an (n+1) cycloid. (To make cycloids roll on the *outside*, fill in negative ‘R’ )
If you want to experiment with this, you can download an Excel sheet:
http://westy31.home.xs4all.nl/ScrapBook/Cycloid.xls
I might update this sheet, tidiness is unfortunately not one of my better skills,,,
Gerard
Dorost! Here’s a deltoid rolling on a cardioid:
زیباست!
And similarly, for any two curves rolling on a third curve, (instead of three circles or lines), we get two moving loci which are always tangent.
A calculus puzzle: When do the two shapes really “roll” on each other?
If you mean, for what choice of two curves rolling on a third (like the small and large moving circles rolling on the fixed small circle in the movie above) will the moving locus be truly rolling on the fixed locus (as if the blue deltoid were truly rolling on the red cardioid) throughout the entire motion … I think the answer is that no proper choice of curves can give that result.
But if you mean, when during the motion can a curve like the blue deltoid really be rolling on the red cardioid, it does happen for an instant in the movie above: each cusp of the deltoid has a velocity of zero at the instant it touches the cardioid.
More generally, if the fixed curve is given by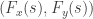 and the second curve rolling on it is given by
and the second curve rolling on it is given by  at time zero (like the large circle in the movie above), and these functions are both parameterised by arc length
at time zero (like the large circle in the movie above), and these functions are both parameterised by arc length  , my calculations give a formula for the magnitude of the velocity of a point on the moving locus, at the point of contact, which contains a factor of:
, my calculations give a formula for the magnitude of the velocity of a point on the moving locus, at the point of contact, which contains a factor of:
Whenever that factor is zero, true rolling will occur. But I don’t believe it’s possible to choose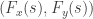 and
and  to make this term identically zero throughout the motion, while keeping the two curves distinct. This is probably easier to see by making use of the fact that the magnitude of the tangent vector to either curve is 1, because of the choice of parameterisation, and so the expression above can be rewritten as:
to make this term identically zero throughout the motion, while keeping the two curves distinct. This is probably easier to see by making use of the fact that the magnitude of the tangent vector to either curve is 1, because of the choice of parameterisation, and so the expression above can be rewritten as:
Having said all that … it would be much more interesting if I’m wrong and there is a counterexample that demonstrates true rolling throughout the motion!
I arrived to almost the same thing. Let the fixed curve be , the second curve (like the big circle above) be
, the second curve (like the big circle above) be  (at time zero) and the first curve be
(at time zero) and the first curve be  (at time zero). The rolling happens in two cases: at the cusps and when
(at time zero). The rolling happens in two cases: at the cusps and when  and
and  have the same curvature at the point of contact. This shows that the shapes cannot roll in a time interval, except when
have the same curvature at the point of contact. This shows that the shapes cannot roll in a time interval, except when  and
and  have some identical arcs which match together (not an interesting case).
have some identical arcs which match together (not an interesting case). by
by 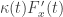 , we arrive to this conclusion.
, we arrive to this conclusion. be the moving point and
be the moving point and  be the common contact point. Let
be the common contact point. Let 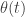 be the angular speed of rotation of the whole curve
be the angular speed of rotation of the whole curve  at time
at time  and
and  be the same for
be the same for  . The magnitude of
. The magnitude of 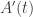 is just
is just  . Similarly, the magnitude of the velocity of the moving point on the moving locus is
. Similarly, the magnitude of the velocity of the moving point on the moving locus is  . So either we should have
. So either we should have  or
or  . The former case corresponds to cusps and the latter case happens when the curvature of
. The former case corresponds to cusps and the latter case happens when the curvature of  and
and  are equal at time
are equal at time  .
.
In your calculations, if we substitute
I used another method which arrived to the physical interpretation of rolling. Let
That’s a nice, clear account! It’s much better to rewrite the second derivative in terms of the curvature.
Here’s the result of two equal-sized circles rolling on an ellipse whose minimum radius of curvature is equal to that of the circles. There are 4 points in each cycle when the moving locus is truly rolling on the fixed locus: three involving cusps, and one that is due solely to the matching radii of curvature.
Curvature of a hypotrochoid:
http://www.math.hmc.edu/math142-01/mellon/curves_and_surfaces/curves/hypotrochoid.html
As a result of my above comment, the length of an arc of a -hypocycloid is
-hypocycloid is 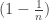 time the length of an arc of a cycloid.
time the length of an arc of a cycloid.
I think this is really pretty. So this is n+1 cusps rolling on n cusps.
It is interesting that the deltoid has to roll around three times to get back to where it was. Can the Tusi couple line roll around the cardioid or vice versa?
Well, correction, the cardioid has negative number of cusps.
Yes. Look at this comment. The claim is true. For an intuitive justification, note that rolling a shape on a curve is infinitesimally like rotating it about the contact point.
And here’s a chorus line of cardioids rolling on a cycloid:
And here’s all three kinds of curve combined: a cardioid and a deltoid rolling together on a cycloid:
Cool toys.
Design a clock with hour and minute hand to build.
These animations are really awesome and fun to look at! My two-year old couldn’t get enough. Would you guys be willing to release these under a Wikimedia Commons-compatible license, and letting me upload them there? CC0 (public domain) would be best, but CC-BY (attribution) or CC-BY-SA (attribution, share-alike) would also work.
I’ve put three of the movies I made on Wikimedia Commons:
(Click to go to the files on Wikimedia Commons.)
Nice, thank you! I added one to the Hypocycloid article.
Great! I polished up your wording. It would be nice if someone could peruse this article of mine:
• John Baez, Deltoid rolling inside astroid, Visual Insight blog, http://blogs.ams.org/visualinsight/2013/12/01/deltoid-rolling-inside-astroid/
see if it makes sense, and maybe add it as a reference to the Wikipedia section Hypocycloid: relationship to group theory.
My article contains proofs of the facts asserted in that Wikipedia section. I’m reluctant to add a link myself since there’s a ban on putting ones own work on Wikipedia, even though this is mainly my exposition of some work of Greg’s. (Am I being too cautious?)
Great! From the very start, rolling hypocycloid images have fascinated people here. Here is the number of views of this blog per hour, shortly after this article was posted:
I added your ref. You are not being too cautious — it’s always a good idea to let someone else add a citation to your own work.
What kind of software tools do people use here for generating these nice animations?
I use Mathematica, which is a (fairly expensive) general purpose program for performing symbolic mathematics.
I’d be surprised if there aren’t lots of much cheaper programs that can do these kinds of simple animations, but having bought Mathematica for other reasons, I haven’t gone looking for them myself.
I used the open source software Geogebra. The deltoid can be drawn using the Curve command:
Curve[2cos(t) + cos(-2t), 2sin(t) + sin(-2t), t, 0, 2 pi]
You can rotate and animate it nicely. However, for exporting the animations I had to use screen capture and convert it to gif with other software. It also exports to applets.
I found out that Geogebra can export directly to Gif animation. It is a very useful tool.
I make pictures with Excel. This is mainly because I use it also for my job as an engineer. You can export single pictures to GIF, then you can combine them into an animated GIF using for example the free program ‘Unfreeze’.
Gerard
Perhaps the cycloid should be called Heartoid?
:)
Add a bearing and a clutch to one of the circles to allow sliding.
Engage clutch at points of zero sliding.
removes sliding-friction-heat-failure problem
All power can be transferred in a duty cycle, coasting while sliding.
In reality this is only how it transfers power anyway in these type designs. If you do surface friction/stiction leads to galling of surface when large forces are attempted to be transferred during sliding at oblique angles.
very cool images. thanks
Ron Davison
Over on G+, Malin Christersson writes:
Make sure to check out her images at http://goo.gl/iYYd6b and http://goo.gl/Z7eJL7, too! They’re versions of images here, but they’re very well-done—made using Geogrebra.
These are just exquisite. There’s something so mesmerizing and meditative about these images (I’m listening to ambient music as I observe their unhurried motion). Bravo, Malin!
I have a new picture that has an interesting feature; It is an n-hypocycloid moving in an (n-1) epicycloid. It has the property that all cusps (both inner and outer) touch the other curve:
Gerard
More fun with epicycloids and hypocycloids:
Math is natures’ finest language!
Gerard Westendorp has some variants, where the inner object stays fixed. He can do it with cycloids:
or hypocycloids:
Thanks for posting it on Azimuth, the birth place of rolling cycloids. I made a post explaining how to fix the center object:
https://plus.google.com/100749485701818304238/posts/b1sSHLafDwq
Gerard
Check this out for some beautiful generalisations, as well as applications:
http://www2.mat.dtu.dk/people/J.Gravesen/MoineauPump/
It includes new ways of generating shapes that fit exactly as they roll, and make this into a helix, applicable in pumps.
Thanks, Gerard! Nice images, like this:
(Click on the picture for details.)
After playing around with cycloids, I messed around and made some graphs in desmos. https://www.desmos.com/calculator/veqhjsui3b
Nice! Thanks!
[…] This page is my implementation inspired by this post. […]
Nice!
Here’s a a nice use of web browsers to let people play with rolling hypocycloids and epicycloids:
• Malin Christensen, Rolling hypocycloids and epicycloids, 18 November 2015.
It’s so old I’m surprised I hadn’t seen it before! Or maybe I had and I’ve forgotten. It was brought to my attention by Alok Tiwari on G+.
Here’s a valentine cardioid animation for your enjoyment!
Nice! Thanks! Happy Valentine’s Day, everyone!
i really like the graphics, i want to know about the equations of them.
glad to find a name for this mechanism :-)
That’s a nice video!