Today I’d like to start telling you about some research Jacob Biamonte and I are doing on stochastic Petri nets, quantum field theory, and category theory. It’ll take a few blog entries to cover this story, which is part of a larger story about network theory.
Stochastic Petri nets are one of many different diagrammatic languages people have evolved to study complex systems. We’ll see how they’re used in chemistry, molecular biology, population biology and queuing theory, which is roughly the science of waiting in line. If you’re a faithful reader of this blog, you’ve already seen an example of a Petri net taken from chemistry:

It shows some chemicals and some reactions involving these chemicals. To make it into a stochastic Petri net, we’d just label each reaction by a nonnegative real number: the reaction rate constant, or rate constant for short.
In general, a Petri net will have a set of states, which we’ll draw as yellow circles, and a set of transitions, which we’ll draw as blue rectangles. Here’s a Petri net from population biology:

Now, instead of different chemicals, the states are different species. And instead of chemical reactions, the transitions are processes involving our species.
This Petri net has two states: rabbit and wolf. It has three transitions:
• In birth, one rabbit comes in and two go out. This is a caricature of reality: these bunnies reproduce asexually, splitting in two like amoebas.
• In predation, one wolf and one rabbit come in and two wolves go out. This is a caricature of how predators need to eat prey to reproduce.
• In death, one wolf comes in and nothing goes out. Note that we’re pretending rabbits don’t die unless they’re eaten by wolves.
If we labelled each transition with a rate constant, we’d have a stochastic Petri net.
To make this Petri net more realistic, we’d have to make it more complicated. I’m trying to explain general ideas here, not realistic models of specific situations. Nonetheless, this Petri net already leads to an interesting model of population dynamics: a special case of the so-called ‘Lotka-Volterra predator-prey model’. We’ll see the details soon.
More to the point, this Petri net illustrates some possibilities that our previous example neglected. Every transition has some ‘input’ states and some ‘output’ states. But a state can show up more than once as the output (or input) of some transition. And as we see in ‘death’, we can have a transition with no outputs (or inputs) at all.
But let me stop beating around the bush, and give you the formal definitions. They’re simple enough:
Definition. A Petri net consists of a set of states and a set
of transitions, together with a function
saying how many copies of each state shows up as input for each transition, and a function
saying how many times it shows up as output.
Definition. A stochastic Petri net is a Petri net together with a function
giving a rate constant for each transition.
Starting from any stochastic Petri net, we can get two things. First:
• The master equation. This says how the probability that we have a given number of things in each state changes with time.
Since stochastic means ‘random’, the master equation is what gives stochastic Petri nets their name. The master equation is the main thing I’ll be talking about in future blog entries. But not right away!
Why not?
In chemistry, we typically have a huge number of things in each state. For example, a gram of water contains about water molecules, and a smaller but still enormous number of hydroxide ions (OH–), hydronium ions (H3O+), and other scarier things. These things blunder around randomly, bump into each other, and sometimes react and turn into other things. There’s a stochastic Petri net describing all this, as we’ll eventually see. But in this situation, we don’t usually want to know the probability that there are, say, exactly
hydronium ions. That would be too much information! We’d be quite happy knowing the expected value of the number of hydronium ions, so we’d be delighted to have a differential equation that says how this changes with time.
And luckily, such an equation exists—and it’s much simpler than the master equation. So, today we’ll talk about:
• The rate equation. This says how the expected number of things in each state changes with time.
But first, I hope you get the overall idea. The master equation is stochastic: at each time the number of things in each state is a random variable taking values in , the set of natural numbers. The rate equation is deterministic: at each time the expected number of things in each state is a non-random variable taking values in
, the set of nonnegative real numbers. If the master equation is the true story, the rate equation is only approximately true—but the approximation becomes good in some limit where the expected value of the number of things in each state is large, and the standard deviation is comparatively small.
If you’ve studied physics, this should remind you of other things. The master equation should remind you of the quantum harmonic oscillator, where energy levels are discrete, and probabilities are involved. The rate equation should remind you of the classical harmonic oscillator, where energy levels are continuous, and everything is deterministic.
When we get to the ‘original research’ part of our story, we’ll see this analogy is fairly precise! We’ll take a bunch of ideas from quantum mechanics and quantum field theory, and tweak them a bit, and show how we can use them to describe the master equation for a stochastic Petri net.
Indeed, the random processes that the master equation describes can be drawn as pictures:

This looks like a Feynman diagram, with animals instead of particles! It’s pretty funny, but the resemblance is no joke: the math will back it up.
I’m dying to explain all the details. But just as classical field theory is easier than quantum field theory, the rate equation is simpler than the master equation. So we should start there.
The rate equation
If you hand me a stochastic Petri net, I can write down its rate equation. Instead of telling you the general rule, which sounds rather complicated at first, let me do an example. Take the Petri net we were just looking at:

We can make it into a stochastic Petri net by choosing a number for each transition:
• the birth rate constant
• the predation rate constant
• the death rate constant
Let be the number of rabbits and let
be the number of wolves at time
. Then the rate equation looks like this:
It’s really a system of equations, but I’ll call the whole thing “the rate equation” because later we may get smart and write it as a single equation.
See how it works?
• We get a term in the equation for rabbits, because rabbits are born at a rate equal to the number of rabbits times the birth rate constant
.
• We get a term in the equation for wolves, because wolves die at a rate equal to the number of wolves times the death rate constant
.
• We get a term in the equation for rabbits, because rabbits die at a rate equal to the number of rabbits times the number of wolves times the predation rate constant
.
• We also get a term in the equation for wolves, because wolves are born at a rate equal to the number of rabbits times the number of wolves times
.
Of course I’m not claiming that this rate equation makes any sense biologically! For example, think about predation. The terms in the above equation would make sense if rabbits and wolves roamed around randomly, and whenever a wolf and a rabbit came within a certain distance, the wolf had a certain probability of eating the rabbit and giving birth to another wolf. At least it would be make sense in the limit of large numbers of rabbits and wolves, where we can treat
and
as varying continuously rather than discretely. That’s a reasonable approximation to make sometimes. Unfortunately, rabbits and wolves don’t roam around randomly, and a wolf doesn’t spit out a new wolf each time it eats a rabbit.
Despite that, the equations
are actually studied in population biology. As I said, they’re a special case of the Lotka-Volterra predator-prey model, which looks like this:
The point is that while these models are hideously oversimplified and thus quantitatively inaccurate, they exhibit interesting qualititative behavior that’s fairly robust. Depending on the rate constants, these equations can show either a stable equilibrium or stable periodic behavior. And we go from one regime to another, we see a kind of catastrophe called a “Hopf bifurcation”. I explained all this in week308 and week309. There I was looking at some other equations, not the Lotka-Volterra equations. But their qualitative behavior is the same!
If you want stochastic Petri nets that give quantitatively accurate models, it’s better to retreat to chemistry. Compared to animals, molecules come a lot closer to roaming around randomly and having a chance of reacting when they come within a certain distance. So in chemistry, rate equations can be used to make accurate predictions.
But I’m digressing. I should be explaining the general recipe for getting a rate equation from a stochastic Petri net! You might not be able to guess it from just one example. But I sense that you’re getting tired. So let’s stop now. Next time I’ll do more examples, and maybe even write down a general formula. But if you’re feeling ambitious, you can try this now:
Puzzle. Can you write down a stochastic Petri net whose rate equation is the Lotka-Volterra predator-prey model:
for arbitrary ? If not, for which values of these rate constants can you do it?
References
If you want to study a bit on your own, here are some great online references on stochastic Petri nets and their rate equations:
• Peter J. E. Goss and Jean Peccoud, Quantitative modeling of stochastic systems in molecular biology by using stochastic Petri nets, Proc. Natl. Acad. Sci. USA 95 (June 1998), 6750-6755.
• Jeremy Gunawardena, Chemical reaction network theory for in-silico biologists.
• Martin Feinberg, Lectures on reaction networks.
I should admit that the first two talk about ‘chemical reaction networks’ instead of Petri nets. That’s no big deal: any chemical reaction network gives a Petri net in a pretty obvious way. You can probably figure out how; if you get stuck, just ask.
Also, I should admit that Petri net people say place where I’m saying state.
Here are some other references, which aren’t free unless you have an online subscription or access to a library:
• Peter J. Haas, Stochastic Petri Nets: Modelling, Stability, Simulation, Springer, Berlin, 2002.
• F. Horn and R. Jackson, General mass action kinetics, Archive for Rational Mechanics and Analysis 47 (1972), 81–116.
• Ina Koch, Petri nets – a mathematical formalism to analyze chemical reaction networks, Molecular Informatics 29 (2010), 838–843.
• Darren James Wilkinson, Stochastic Modelling for Systems Biology, Taylor & Francis, New York, 2006.

I’ll be curious to see how your analogy compares to the relation I’ve encountered in my own research between master equations and field theory. Readings:
Formalism:
Doi, M (1976). Second-quantization representation for classical many-particle systems. Journal of Physics A 9, 9: 1465-77.
Doi, M (1976). Stochastic theory of diffusion-controlled reactions. Journal of Physics A 9, 9: 1479-95.
Peliti, L (1985). Path integral approach to birth-death processes on a lattice. Journal de Physique 46 1469-83.
Cardy, J (1996). Renormalization group approach to reaction-diffusion problems. arXiv:cond-mat/9607163.
Mattis, D. C. and M. L. Glasser (1998). The uses of quantum field theory in diffusion-limited reactions. Reviews of Modern Physics 70, 3: 979-1001.
Applications:
Täuber, U et al. (2005). Applications of Field-Theoretic Renormalization Group Methods to Reaction-Diffusion Problems. Journal of Physics A 38, 17: R79. arXiv:cond-mat/0501678.
Buice, M. A. and J. D. Cowan (2007). Field-theoretic approach to fluctuation effects in neural networks. Physical Review E 75: 051919.
Buice, M. A. and J. D. Cowan (2009). Statistical mechanics of the neocortex. Progress in Biophysics and Molecular Biology 99: 53-86.
Dodd, P. J. and N. M. Ferguson (2009). A Many-Body Field Theory Approach to Stochastic Models in Population Biology. PLoS ONE 4, 9: e6855.
The basic idea is that we want to know how many units of something there are, and what the probabilities are for that discrete number of things to change over time. One way to understand a probability distribution defined over the nonnegative integers is to hang it on a clothesline and write its generating function. But, as we all know, the reason generating functions are so much fun is that the operations of dropping a billiard ball into a pocket and pulling one out do not commute: there’s one more way to perform those operations in one order than in the other. This is the same algebra as that of the operators “multiply by ” and “differentiate with respect to
” and “differentiate with respect to  “, and it is also the Heisenberg algebra of the quantum harmonic oscillator’s creation and annihilation operators. So, instead of multiplying occupation probabilities by powers of some formal variable
“, and it is also the Heisenberg algebra of the quantum harmonic oscillator’s creation and annihilation operators. So, instead of multiplying occupation probabilities by powers of some formal variable  , we can use them as coefficients of “kets” formed by acting multiple times with a “creation operator” on a “vacuum state”. Then, we can steal techniques from many-body quantum mechanics (coherent state path integrals, renormalization group arguments, etc.) to pose and, sometimes, answer interesting questions. The more physics-y language turns out useful when things can be in different places and interact when they bump into one another.
, we can use them as coefficients of “kets” formed by acting multiple times with a “creation operator” on a “vacuum state”. Then, we can steal techniques from many-body quantum mechanics (coherent state path integrals, renormalization group arguments, etc.) to pose and, sometimes, answer interesting questions. The more physics-y language turns out useful when things can be in different places and interact when they bump into one another.
It sounds like you, and perhaps some of these authors, already understand much of what I’m trying to explain. As you may or may not recall, the combinatorial significance of generating functions, and the way
follows from the fact that “there’s one more way to put a rock in a bag and then pull one out than to pull one out and then put one in”, was the starting-point for what James Dolan and I did in our paper From finite sets to Feynman diagrams. The idea was to categorify quantum mechanics by working with combinatorial structures directly instead of their generating functions—a kind of fat-free approach where we don’t fry the combinatorics in the oil of linear algebra. We later saw this as a special case of groupoidification.
So, I’m still talking about the same darn stuff, but taking even more seriously the idea that there’s nothing particular ‘quantum’ about the relations
It applies to rocks and wolves as well as photons. But where quantum physicists have developed the formalism of Fock space and annihilation/creation operators to study this idea, computer scientists and chemists use ‘stochastic Petri nets’ and ‘chemical reaction networks’. So, I want to unify and clarify all this work.
While your long list of references is fairly demoralizing at first glance, I hope that by thinking harder about the fundamentals, and knowing the kinds of math it takes to talk about these ideas with the precision and generality they deserve, we can do a few things that haven’t already been done.
Here are a few more references for your list, Blake. I was planning to save these for later, but like a poker player whose bluff has been called, I feel I’d better turn them over now:
• M. Doi, Second quantization representation for classical many-particle systems, J. Phys. A 9 (1976), 1465-1477.
• P. Grassberger, M. Scheunert, Fock-space methods for identical classical objects, Fortschritte der Physik, 28 (1980), 547–578.
These papers discuss applications to diffusion-limited reactions:
• M. Doi, Stochastic theory of diffusion-controlled reactions, J. Phys. A 9 (1976), 1479-1495.
• Daniel C. Mattis and M. Lawrence Glasser, The uses of quantum field theory in diffusion-limited reactions, Reviews of Modern Physics, 70 (1998), 979-1001.
(I see you already have that one.)
• Martin J Howard and Uwe C. Täuber, Real versus imaginary noise in diffusion-limited reactions, J. Phys. A 30 (1997), 7721.
• Ben Vollmayr-Lee, Field theory approach to diffusion-limited reactions, slides and videos of 4 lectures at Nonequilibrium Statistical Mechanics: Fundamental Problems and Applications,
6 – 24 July, 2009, Boulder, Colorado, USA.
* Mauro Mobilia, Ivan T. Georgiev and Uwe Claus Täuber, Fluctuations and correlations in lattice models for predator-prey interaction, Physical Review E 73 (1980) 040903.
• Mauro Mobilia, Ivan T. Georgiev, and Uwe Claus Tauber, Phase transitions and spatio-temporal fluctuations in stochastic lattice Lotka-Volterra models.
(I think you were the one who pointed out the last one or two here, Blake!)
This paper has a fairly up-to-date review of previous work:
• Uwe Claus Täuber, Field-theoretic methods.
The section on history is interesting:
I’m all in favour of unifying and clarifying — and I’m definitely sure that at least a few new results aren’t too far beyond reach!
(I’m still learning my way around these ideas. I should by rights have started four years ago, when I saw Jack Cowan present what became Buice and Cowan (2009) at MIT, and he incidentally mentioned that directed percolation is in the same universality class as Reggeon Field Theory. It wasn’t until about a year ago that one of my own research problems started to look like it required these tools, though, and the time since hasn’t lacked for distractions.)
too funny how the rabbit walks on tip-toes before his predation.
Does it really? I like the idea…
We were thinking of putting a patch of blood on the snow instead of the blue box labelled ‘predation’, but we thought that would be going too far.
I’m going to make a wild-assed guess (and probably get shot out of the sky immediately by a swarm of mathematicians screaming in for the kill) and say:
No, only where the values of the rate constants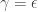
A brave and noble guess!
What do the rest of you folks out there think? Can you prove it, disprove it…?
By the way, I made your equations come out nice-looking by sandwiching the math symbols with
$latex $
(No space between the first dollar sign and the word ‘latex’.) So, for example:
$latex \frac{dx}{dt} = \beta x – \gamma x y $
comes out looking like:
There’s no way to preview your equations, alas — but I can fix ’em if you screw up.
I’m inclined to say you can for arbitrary values (although my understanding is incomplete: see below) if you’re prepared to mess around with the number of arrows linking various boxes and the intrinsic reaction rates.
I’m really going to go out on a limb here, using a concept I remember from long ago, the Kronecker delta (and see if my latex works…):
for arbitrary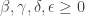 ? As I recall, the Kronecker delta picks out values of
? As I recall, the Kronecker delta picks out values of  and
and  which are the same, so this is equivalent to my statement in words in my first guess. Now to see if the latex is correct…
which are the same, so this is equivalent to my statement in words in my first guess. Now to see if the latex is correct…
I fixed your latex a bit; the most exciting latex mistake was
$latex \frac{d y}{d t} = \delta \sub \gamma \sub \epsilon \epsilon x y – \delta y $
I believe you meant to write
$latex \frac{d y}{d t} = \delta_{\gamma \epsilon} \epsilon x y – \delta y $
There’s no ‘\sub’ command in latex.
As for the actual math…
Let’s see! The Kronecker delta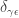 is 1 when
is 1 when  and
and  are equal, and 0 when they’re not equal.
are equal, and 0 when they’re not equal.
So, when they’re equal, we get:
We can get these equations from this stochastic Petri net:
When they’re not equal, we get:
This is the special case of the previous equations where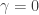 .
.
So yes, your new answer are equivalent to your one. However (since a clue seems to be in order), I think you’re not being bold enough: I believe it’s possible to dream up stochastic Petri nets that give equations
where .
.
Some people have made suggestions, and I’ll comment on them a bit now…
I would need to work out the details but if you have n rabbits and m wolves going into the predation box with m+1 wolves and no rabbits comming out (m << n) you should be able to get epsilon as a rational times gamma.
In particular the obvious case is something like a wolf needs to eat 100 rabbits to reproduce.
Roger wrote:
That’s a good thing to think about.
Suppose we have a stochastic Petri net with just two states, rabbit and wolf, and one transition, which has 1 wolf and 100 rabbits as input, and 2 wolves as output. Say the rate constant is . What rate equation does this give?
. What rate equation does this give?
No takers? Okay, since I haven’t spelled out all the rules maybe folks are shy to venture guesses.
The problem is that with the stochastic Petri net I described, a wolf has to meet and eat 100 rabbits all at once in order to reproduce!
So, if is the number of rabbits and
is the number of rabbits and  the number of wolves, we get
the number of wolves, we get
See why? Our transition has 100 rabbits and 1 wolf as input, so its rate is proportional to . The constant
. The constant  comes in because it describes the rate at which this transition occurs. After the transition happens we have 100 fewer rabbits, so we get a factor of -100 in the equation for rabbits:
comes in because it describes the rate at which this transition occurs. After the transition happens we have 100 fewer rabbits, so we get a factor of -100 in the equation for rabbits:
After this transition happens we have 1 more wolf, so we get a factor of +1 in the equation for wolves:
So, this stochastic Petri net does not give us an equation of the form we’re after, namely:
The problem is that we’re getting a term proportional to , not
, not 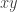 .
.
You see, the idea is that rabbits and wolves are randomly roaming around. The probability that 1 rabbit and 1 wolf come within a certain distance is proportional to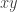 . But the probability that 100 rabbits and 1 wolf come within a certain distance is proportional to
. But the probability that 100 rabbits and 1 wolf come within a certain distance is proportional to  .
.
We can design a Petri net where a wolf could eat 100 rabbits one after another before reproducing, instead of all at once. But it looks different. Do you see what it looks like?
People in Petri net theory think about this sort of thing a lot: for example, I’ve seen a Petri net describing a soft drink machine, where putting in 3 quarters will make the machine give you a can of soda. You can put the quarters in one at a time, as slowly as you like, and when you put in the third quarter the machine delivers a can of soda and resets to its original state (but with one less can of soda).
(This is going to look like a non-sequitur partly as I’ve seen other stuff John has written on the Azimuth Project.)
So the fact your differential equation has an
differential equation has an  term in it is because there’s a rabbit arrow and a wolf arrow going into the predation box. Without going into the full complexities you’re avoiding, is it possible to say what effect multiple arrows coming out have? As an example, suppose there were 3 wolf arrows coming out of the predation box (so wolves always give birth to twins): what would change about the derived differential equations? (My vague suspicion is that the form wouldn’t change, the change would be absorbed into the actual values of the coefficients.)
term in it is because there’s a rabbit arrow and a wolf arrow going into the predation box. Without going into the full complexities you’re avoiding, is it possible to say what effect multiple arrows coming out have? As an example, suppose there were 3 wolf arrows coming out of the predation box (so wolves always give birth to twins): what would change about the derived differential equations? (My vague suspicion is that the form wouldn’t change, the change would be absorbed into the actual values of the coefficients.)
D’oh: as the wolves are the s, it’s the differential equation for that which might change when changing the wolf output arrows.
s, it’s the differential equation for that which might change when changing the wolf output arrows.
David wrote:
Your suspicion is right! Suppose we changed our favorite stochastic Petri net
so that 3 wolves come out of predation instead of 2. Then the transition would occur at the same rate as before, since its inputs are the same. But when it occurred, it would now increase the number of wolves by 2 instead of 1. So, we’d get this rate equation:
instead of the original one, which was:
This counts as progress on my puzzle! We’re now getting a Lotka-Volterra equation
where .
.
So, we can get and we can get
and we can get  . What else can we get? Can we get
. What else can we get? Can we get  ?
?
Let’s see. If “predation”, still consuming one each rabbit and wolf, produces rabbits and
rabbits and  wolves (where originally
wolves (where originally  and
and 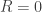 ), then the equations should be
), then the equations should be
So we can easily get Lotka-Volterra with either (called
(called  above) or
above) or  (called
(called  above) zero (or with both zero); but to get them different and positive is tricky, since it requires
above) zero (or with both zero); but to get them different and positive is tricky, since it requires 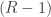 and
and  to have different signs, which means one of them must be -1. So the only ratios they can have are
to have different signs, which means one of them must be -1. So the only ratios they can have are 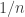 for
for 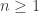 .
.
(Too bad this blog won’t let me edit my comment, to fix the non-parsing equation and clarify a couple things: one of (R-1) and (W-1) must be -1, so the only ratio gamma and epsilon can have (when neither is zero) is 1/n (in either order).)
Hi, Bruce! Great to see you!
(Everybody: this is my old college pal Bruce Smith, one of my best friends in the universe!)
I was feeling a bit sad at how people seemed to have given up on this puzzle after a few initial attempts. But when the going gets tough, the tough get going.
I corrected your LaTeX: oddly, I couldn’t spot the error, but it went away when I retyped that equation. I’m sorry that this blog has no preview feature (not sorry that people can’t go back in time and change their remarks), but alas, that’s how it is.
It looks like you’re attempting a complete analysis of the rate equations that can arise from the class of Petri nets with two states, rabbit and wolf, and three transitions:
• birth (1 rabbit in, 2 rabbits out)
• death (1 wolf in, 0 wolves out)
• predation (1 wolf and 1 rabbit in, rabbits and
rabbits and  wolves out, where
wolves out, where  are arbitrary natural numbers)
are arbitrary natural numbers)
This looks right:
But then you say:
Now you’re assuming that predation either has no rabbits as output, or no wolves as output. But there’s nothing in Petri net theory that demands this: for example, the output is allowed to be 7 rabbits and 3 wolves.
I also believe that to fully answer my original question, one may need to consider a class of Petri nets more general than described above.
Replying to John’s reply:
> … seemed to have given up on this puzzle …
I think not much time has gone by — probably potential solvers are mostly just on vacation.
> … • death (1 wolf in, 2 wolves out)
I’m generally not a big fan of death, but that kind sounds ok …. :-)
> predation (1 wolf and 1 rabbit in, R rabbits and W rabbits out, where R,W are arbitrary natural numbers)
W *wolves* out, but yes. (Though it’s no longer sensible to call it “predation” — it’s just “interaction” now.)
> Now you’re assuming that predation either has no rabbits as output, or no wolves as output. But there’s nothing in Petri net theory that demands this: for example, the output is allowed to be 7 rabbits and 3 wolves.
There’s nothing in Petri net theory that demands it, but there’s something in the problem that demands it. R-1 and W-1 need to be nonzero and to have opposite sign. (Assuming you got all the signs and conditions right in your Lotka-Volterra equations. I’m just trusting you on that.)
Thanks for catching those typos, Bruce. Let me correct them here, just for the record.
The stochastic Petri net with two states—rabbits and wolves—and 3 transitions:
• birth (1 rabbit in, 2 rabbits out), with rate constant
• death (1 wolf in, 0 wolves out), with rate constant
• combat (1 wolf and 1 rabbit in, rabbits and
rabbits and  wolves out, where
wolves out, where  are arbitrary natural numbers), with rate constant
are arbitrary natural numbers), with rate constant  .
.
gives this rate equation:
You wrote:
Okay, now I see what you meant. Yes, if we want a stochastic Petri net of the above sort to produce a rate equation of the form
with then we need one of
then we need one of  and
and  to be zero.
to be zero.
But as you’ve later seen, it’s very interesting to consider stochastic Petri nets with two or more combat processes. And then dropping this constraint on and
and  may be allowed, though it’s not necessary for solving the puzzle.
may be allowed, though it’s not necessary for solving the puzzle.
Since only Bruce has had a go, here’s a way I think you can get . Suppose rabbits start to fight back: they’re so small they never win but half the time they “take the wolf with them”. Then we’ve now got a “predation” process as before and a “mutual destruction” process with one rabbit and one wolf going in and nothing coming out. If the rate for “combat encounters” is
. Suppose rabbits start to fight back: they’re so small they never win but half the time they “take the wolf with them”. Then we’ve now got a “predation” process as before and a “mutual destruction” process with one rabbit and one wolf going in and nothing coming out. If the rate for “combat encounters” is  , then the rate for these two processes is
, then the rate for these two processes is  . If think if you do the derivation you get
. If think if you do the derivation you get  .
.
Perhaps someone might like to have a go at what’s possible for the differential equations if you’re allowed as many combat “processes” (which might actually be the same process) in the Petri net as you want? (Of course, arguably doing this is a hack rather than elegant modelling.)
David wrote:
Now you’re talking! Of course biological realism is not the point of this exercise, but if we don’t want to envision killer rabbits, we can imagine that sometimes a wolf chases a wolf, kills it, but gets so lost and tired in the process that it gets separated from the pack and dies.
We can also imagine a different stochastic Petri net containing a process where the wolf gets exhausted and dies but the rabbit survives. Or… it’s mathematically equivalent… the rabbit eats the wolf!
We can also imagine stochastic Petri nets containing all these processes, with various rate constants.
That’s if they’re each equally likely, right? There’s no reason they have to be equally likely, but we’re allowed to assume that if we want.
That sounds like a great thing.
A bit of biological realism for you:
Actually, the above construction isn’t quite right: that actually gives (since you gain 2 wolves at the same time as you lose 2 wolves). Making the wolf survive
(since you gain 2 wolves at the same time as you lose 2 wolves). Making the wolf survive 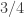 (ie, predation process has a rate of
(ie, predation process has a rate of 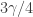 ) of the time does give
) of the time does give  .
.
> … if you’re allowed as many combat “processes” as you want?
If my initial reply was right (except in my assumption that only one combat process need be considered), then each combat process can give you an arbitrary gamma/epsilon coefficient pair whose ratio is either 1/n or n/1, for any n, or with either one being zero; and having multiple processes just adds up these coefficient pairs. In that case I think it’s obvious you should be able to get any coefficents with a rational ratio… and maybe still more, I’m not sure, but clearly you can *approximate* any coefficients.
Oh, I was being silly (at the end of my very last comment) — if you include one combat process with gamma zero and one with epsilon zero, of course you can get them to add up to any coefficient pair.
You can still get a *single* combat process to have a 1/n or n/1 ratio of those coefficients (but no other ratio, if both are nonzero), but there’s nothing special about having only a single combat process, since it would make sense to generalize Petri net transitions to allow probability distributions over output state sets, but there’s no need for that since they would be equivalent to multiple transitions (appropriately weighted) with the same inputs and different fixed outputs.
That’s my understanding. (Whilst I don’t know about stochastic Petri nets, I’ve done stuff with probabilistic graphical models — generalisations of markov processes — and it looks like a lot of the “tricks” carry over.) To take what’s happening in the simple case “predation” and “mutual destruction” case, you’re taking a process which has a probabilistic choice of outputs and replacing it with two deterministic processes, one for each output. In the large limit there’s no “operational” problem with this, but it may make it more difficult to discern the original process behind the model.
Dave wrote:
That’s right.
Okay, you guys solved the puzzle! I’ll post an official summary solution below.
Hi John,
I have a couple of questions that I hope you could indulge.
1. You defined a Petri net as two functions. You draw them as graphs with vertices labelled by circles or squares. Strictly speaking these things are not the same. Is there a category of Petri nets and a functor that embeds it into directed graphs with colored vertices?
Given a Petri net, you have written an ODE in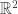 . Is there a functor from Petri nets to ODEs? If not, what is being done?
. Is there a functor from Petri nets to ODEs? If not, what is being done?
By the way, I don’t think there is a nice functor from directed graphs to ODEs. There is a functor going from ODEs to directed graphs if you require your ODEs to have a certain amount of modularity (which has nothing to do with modular forms, but I don’t know how to say it better).
Hi, Eugene!
(Everybody: this is Eugene Lerman, the expert on symplectic geometry and stuff like that!)
I think I’m doing something less bad that you think, though I could be making a mistake.
I start with two functions
and
saying how many times each state appears as the input or output of each transition.
I draw this information as a set of blue squares, a set
of blue squares, a set  of yellow circles, a total of
of yellow circles, a total of  arrows from each circle
arrows from each circle 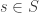 to each square
to each square  , and a total of
, and a total of  arrows from each square
arrows from each square  to each circle
to each circle 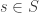 .
.
Apart from the cute artistic touches, this is just a bipartite directed multigraph, by which I mean a set of vertices equipped with a specific way of writing it as the disjoint union of sets and
and  , together with a set of directed edges, such that any edge goes either from an element of
, together with a set of directed edges, such that any edge goes either from an element of  to an element of
to an element of  , or from an element of
, or from an element of  to an element of
to an element of  .
.
And if I’m not making a mistake, there’s an obvious category of Petri nets which is equivalent to the obvious category of bipartite directed multigraphs.
(And by the way, I personally like to use ‘graph’ to mean what I’m calling a ‘directed multigraph’ here, which in turn is the same as a pair of sets ,
,  and a pair of functions
and a pair of functions  . But people use ‘graph’ in so many ways that right now I’m saying ‘directed multigraph’ to be clear, since that’s what the god who knows all does.)
. But people use ‘graph’ in so many ways that right now I’m saying ‘directed multigraph’ to be clear, since that’s what the god who knows all does.)
I believe so, if by ‘directed graph’ you mean what I’m now calling a ‘directed multigraph’. However, I am simply not interested in the category of all directed multigraphs with 2-colorings of the vertices, since the includes directed multigraphs that allow edges from a transition to another transition, or from a state to another state.
It’s either a functor or it ain’t worth beans, eh?
I haven’t thought about this much. I’d feel duty-bound to commit hara-kiri if I weren’t describing a functor from the groupoid of stochastic Petri nets to the groupoid of ‘vector spaces equipped with vector field’. That’s all I really care about now. But it’s possible that this functor extends to some category of stochastic Petri nets that includes noninvertible morphisms.
[…] Network Theory (Part 2) […]
I wasn’t trying to imply that you are doing anything illegal in your discussion of Petri nets as bipartite (directed multi) graphs. I was only nudging you to spell it out, because I am lazy :).
Is it correct to think that the category of bipartite graphs is a slice category where
where  is the category of directed multigraphs and C is a graph with two vertices (square, rectangle) and two arrows? And this “is” your category of Petri nets?
is the category of directed multigraphs and C is a graph with two vertices (square, rectangle) and two arrows? And this “is” your category of Petri nets?
I was going to say more, but my son just came over and is now studying your post.
Eugene wrote:
That sounds correct—though again, I’ve paid no attention to the noninvertible morphisms in this category.
To get a differential equation I need a stochastic Petri net. But there’s a huge literature on plain Petri nets.
Also: I should warn you that there are probabily evil people lurking out there who treat ‘being bipartite’ as a property of a graph rather than a structure. For us it’s crucial to treat it as a structure.
Here is a related reference that John found and showed me a while back:
* Vladimiro Sassone (http://www.ecs.soton.ac.uk/people/vs), On the category of Petri net computations, 6th International Conference on Theory and Practice of Software Development, Proceedings of TAPSOFT ‘95_, Lecture Notes in Computer Science 915, Springer, Berlin, pp. 334-348. (http://eprints.ecs.soton.ac.uk/11951/1/strong-conf.pdf)
The same structure occurs in the more general setting of:
Lucas Dixon, Aleks Kissinger. Open Graphs and Monoidal Theories
which has been specifically developed for dealing with certain subtleties (e.g. scalars) when considering the diagrams in compact categories as graphs. (I am actually currently sitting in a talk about this.)
Bruce Smith and David Tweed solved the puzzle. Let me write up the solution, just for the record.
Answer. We can find a stochastic Petri net that does the job for any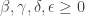 .
.
In fact we can find one that does the job for any possible value of . But to keep things simple, let’s just solve the original puzzle.
. But to keep things simple, let’s just solve the original puzzle.
We’ll consider a stochastic Petri net with two states, rabbit and wolf, and four transitions:
• birth (1 rabbit in, 2 rabbits out), with rate constant
• death (1 wolf in, 0 wolves out), with rate constant
• jousting (1 wolf and 1 rabbit in, rabbits and
rabbits and  wolves out, where
wolves out, where  are arbitrary natural numbers), with rate constant
are arbitrary natural numbers), with rate constant 
• dueling (1 wolf and 1 rabbit in,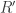 rabbits and
rabbits and 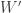 wolves out, where
wolves out, where 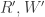 are arbitrary natural numbers) with rate constant
are arbitrary natural numbers) with rate constant 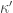 .
.
All these rate constants are nonnegative.
This gives the rate equation
This is flexible enough to do the job.
For example, let’s assume that when they joust, the massive, powerful wolf always kills the rabbit, and then eats the rabbit and has one offspring ( and
and  ). And let’s assume that in a duel, the lithe and clever rabbit always kills the wolf, but does not reproduce afterward (
). And let’s assume that in a duel, the lithe and clever rabbit always kills the wolf, but does not reproduce afterward (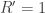 ,
, 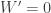 ).
).
Then we get
This handles the equations
where and
and  . In other words, the cases where more rabbits die due to combat than wolves get born!
. In other words, the cases where more rabbits die due to combat than wolves get born!
I’ll let you handle the cases where fewer rabbits die than wolves get born.
If we also include a death process for rabbits and birth process for wolves, we can get the fully general Lotka-Volterra equations:
It’s worth noting that biologists like to study these equations with different choices of sign for the constants involved: the predator-prey Lotka-Volterra equations and the competitive Lotka-Volterra equations.
Since, and
and  , shouldn’t
, shouldn’t  ?
?
Yes, thanks! I’ll fix this in the website version and the PDF file.
Now that the puzzle is solved, I wonder if there is a way to find a “minimal” Petri net that gets the job done.
I think it ends up as to a problem in the theory of equations: the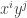 terms are come from processes with different numbers of inputs, so you can solve for their Petri net processes independently without problems. For a given term, the
terms are come from processes with different numbers of inputs, so you can solve for their Petri net processes independently without problems. For a given term, the  equation coefficient is
equation coefficient is 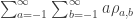 and the
and the  term is
term is  , where
, where  is the rate for the process with
is the rate for the process with 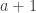
 outputs and
outputs and 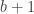
 outputs and we expect all but a finite number of them to be zero. So it’s a case of finding the matrix of
outputs and we expect all but a finite number of them to be zero. So it’s a case of finding the matrix of 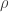 values which both solves of those two equations and has a minimal “norm” in some sense. I’m not up-to-date on how that problem is best solved.
values which both solves of those two equations and has a minimal “norm” in some sense. I’m not up-to-date on how that problem is best solved.
[…] we saw last time, a Petri net is a gadget that describes things of different kinds and processes that turns a bunch […]
ArXiv paper today – Lagrangians for biological models – which looks for Lagrangians of models such as Volterra-Lotka.
Thanks David!
[…] John and his colleagues have been talking about reaction networks as Petri nets in the network theory series on this blog. As discussed in part 2 of that series, a Petri net is a diagram like this […]
[…] We thus see that ATP hydrolysis is in no way affecting the ratio of to Intuitively, there is no coupling because the two reactions proceed independently. This ‘independence’ is clearly visible if we draw the reaction network as a so-called Petri net: […]