Coupling Through Emergent Conservation Laws (Part 3)

joint post with Jonathan Lorand, Blake Pollard, and Maru Sarazola

Last time we gave a quick intro to the chemistry and thermodynamics we’ll use to understand ‘coupling’. Now let’s really get started!

Suppose that we are in a setting in which some reaction

\mathrm{X} + \mathrm{Y} \mathrel{\substack{\alpha_{\rightarrow} \\\longleftrightarrow\\ \alpha_{\leftarrow}}} \mathrm{XY}

takes place. Let’s also assume we are interested in the production of \mathrm{XY} from \mathrm{X} and \mathrm{Y}, but that in our system, the reverse reaction is favored to happen. This means that that reverse rate constant exceeds the forward one, let’s say by a lot:

\alpha_\leftarrow \gg \alpha_\to

so that in equilibrium, the concentrations of the species will satisfy

\displaystyle{ \frac{[\mathrm{XY}]}{[\mathrm{X}][\mathrm{Y}]}\ll 1 }

which we assume undesirable. How can we influence this ratio to get a more desired outcome?

This is where coupling comes into play. Informally, we think of the coupling of two reactions as a process in which an endergonic reaction—one which does not ‘want’ to happen—is combined with an exergonic reaction—one that does ‘want’ to happen—in a way that improves the products-to-reactants concentrations ratio of the first reaction.

An important example of coupling, and one we will focus on, involves ATP hydrolysis:

\mathrm{ATP} + \mathrm{H}_2\mathrm{O} \mathrel{\substack{\beta_{\rightarrow} \\\longleftrightarrow\\ \beta_{\leftarrow}}} \mathrm{ADP} + \mathrm{P}_{\mathrm{i}} + \mathrm{H}^+

where ATP (adenosine triphosphate) reacts with a water molecule. Typically, this reaction results in ADP (adenosine diphosphate), a phosphate ion \mathrm{P}_{\mathrm{i}} and a hydrogen ion \mathrm{H}^+. To simplify calculations, we will replace the above equation with

\mathrm{ATP} \mathrel{\substack{\beta_{\rightarrow} \\\longleftrightarrow\\ \beta_{\leftarrow}}} \mathrm{ADP} + \mathrm{P}_{\mathrm{i}}

since suppressing the bookkeeping of hydrogen and oxygen atoms in this manner will not affect our main points.

One reason ATP hydrolysis is good for coupling is that this reaction is strongly exergonic:

\beta_\to \gg \beta_\leftarrow

and in fact so much that

\displaystyle{ \frac{\beta_\to}{\beta_\leftarrow} \gg \frac{\alpha_\leftarrow}{\alpha_\to} }

Yet this fact alone is insufficient to explain coupling!

To see why, suppose our system consists merely of the two reactions

\begin{array}{ccc} \mathrm{X} + \mathrm{Y} & \mathrel{\substack{\alpha_{\rightarrow} \\\longleftrightarrow\\ \alpha_{\leftarrow}}} & \mathrm{XY} \\ \\ \mathrm{ATP} & \mathrel{\substack{\beta_{\rightarrow} \\\longleftrightarrow\\ \beta_{\leftarrow}}} & \mathrm{ADP} + \mathrm{P}_{\mathrm{i}} \label{beta} \end{array}

happening in parallel. We can study the concentrations in equilibrium to see that one reaction has no influence on the other. Indeed, the rate equation for this reaction network is

\begin{array}{ccl} \dot{[\mathrm{X}]} & = & -\alpha_\to [\mathrm{X}][\mathrm{Y}]+\alpha_\leftarrow [\mathrm{XY}]\\ \\ \dot{[\mathrm{Y}]} & = & -\alpha_\to [\mathrm{X}][\mathrm{Y}]+\alpha_\leftarrow [\mathrm{XY}]\\ \\ \dot{[\mathrm{XY}]} & = & \alpha_\to [\mathrm{X}][\mathrm{Y}]-\alpha_\leftarrow [\mathrm{XY}]\\ \\ \dot{[\mathrm{ATP}]} & =& -\beta_\to [\mathrm{ATP}]+\beta_\leftarrow [\mathrm{ADP}][\mathrm{P}_{\mathrm{i}}]\\ \\ \dot{[\mathrm{ADP}]} & = &\beta_\to [\mathrm{ATP}]-\beta_\leftarrow [\mathrm{ADP}][\mathrm{P}_{\mathrm{i}}]\\ \\ \dot{[\mathrm{P}_{\mathrm{i}}]} & = &\beta_\to [\mathrm{ATP}]-\beta_\leftarrow [\mathrm{ADP}][\mathrm{P}_{\mathrm{i}}] \end{array}

When concentrations are constant, these are equivalent to the relations

\displaystyle{ \frac{[\mathrm{XY}]}{[\mathrm{X}][\mathrm{Y}]} = \frac{\alpha_\to}{\alpha_\leftarrow} \ \ \text{ and } \ \ \frac{[\mathrm{ADP}][\mathrm{P}_{\mathrm{i}}]}{[\mathrm{ATP}]} = \frac{\beta_\to}{\beta_\leftarrow} }

We thus see that ATP hydrolysis is in no way affecting the ratio of [\mathrm{XY}] to [\mathrm{X}][\mathrm{Y}]. Intuitively, there is no coupling because the two reactions proceed independently. This ‘independence’ is clearly visible if we draw the reaction network as a so-called Petri net:

So what really happens when we are in the presence of coupling? Stay tuned for the next episode!

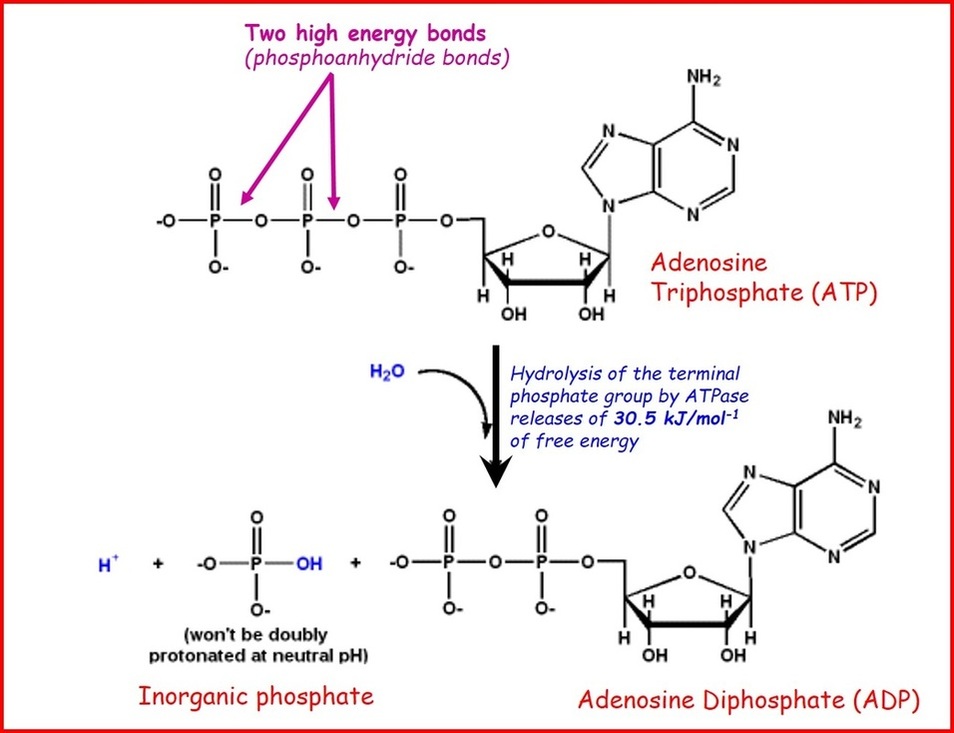
By the way, here’s what ATP hydrolysis looks like in a bit more detail, from a website at Loreto College:


 

 
The paper:

• John Baez, Jonathan Lorand, Blake S. Pollard and Maru Sarazola,
Biochemical coupling through emergent conservation laws.

The blog series:

• Part 1 – Introduction.

• Part 2 – Review of reaction networks and equilibrium thermodynamics.

• Part 3 – What is coupling?

• Part 4 – Interactions.

• Part 5 – Coupling in quasiequilibrium states.

• Part 6 – Emergent conservation laws.

• Part 7 – The urea cycle.

• Part 8 – The citric acid cycle.

This entry was posted on Thursday, June 28th, 2018 at 6:09 pm and is filed under biology, chemistry, information and entropy, mathematics, networks. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

3 Responses to Coupling Through Emergent Conservation Laws (Part 3)

  1. Coupling Through Emergent Conservation Laws (Part 4) | Azimuth says:
    29 June, 2018 at 12:00 pm

    Taking into account this more complicated set of reactions, which are interacting with each other, is still not enough to explain the phenomenon of coupling. To see this, let’s consider the rate equation for the system comprised of all four reactions. To write it down neatly, let’s introduce reaction velocities that say the rate at which each forward reaction is taking place, minus the rate of the reverse reaction:

    \begin{array}{ccl} J_\alpha &=& \alpha_\to [\mathrm{X}][\mathrm{Y}] - \alpha_\leftarrow [\mathrm{XY}] \\ \\ J_\beta &=& \beta_\to [\mathrm{ATP}] - \beta_\leftarrow [\mathrm{ADP}] [\mathrm{P}_{\mathrm{i}}] \\ \\ J_\gamma &=& \gamma_\to [\mathrm{ATP}] [\mathrm{X}] - \gamma_\leftarrow [\mathrm{ADP}] [\mathrm{XP}_{\mathrm{i}} ] \\ \\ J_\delta &=& \delta_\to [\mathrm{XP}_{\mathrm{i}} ] [\mathrm{Y}] - \delta_\leftarrow [\mathrm{XY}] [\mathrm{P}_{\mathrm{i}}] \end{array}

    All these follow from the law of mass action, which I explained last time. Remember, this says that any reaction occurs at a rate equal to its rate constant times the product of the concentrations of the species involved. So, for example, this reaction

    \mathrm{XP}_{\mathrm{i}} +\mathrm{Y} \mathrel{\substack{\delta_{\rightarrow} \\\longleftrightarrow\\ \delta_{\leftarrow}}} \mathrm{ADP} + \mathrm{P}_{\mathrm{i}}

    goes forward at a rate equal to \delta_\rightarrow [\mathrm{XP}_{\mathrm{i}}][\mathrm{Y}], while the reverse reaction occurs at a rate equal to \delta_\leftarrow [\mathrm{ADP}] [\mathrm{P}_{\mathrm{i}}]. So, its reaction velocity is

    J_\delta = \delta_\to [\mathrm{XP}_{\mathrm{i}} ] [\mathrm{Y}] - \delta_\leftarrow [\mathrm{XY}] [\mathrm{P}_{\mathrm{i}}]

    Reply
  2. Toby Bartels says:
    30 June, 2018 at 4:12 am

    How do I get notified of new comments via email without making a comment?

    Reply
    • John Baez says:
      30 June, 2018 at 9:38 pm

      I’m not sure. There’s an RSS feed at the right of this page that lets you get notified about comments, also available here. There may be a way to get notified by email.

      Reply

You can use Markdown or HTML in your comments. You can also use LaTeX, like this: $latex E = m c^2 $. The word 'latex' comes right after the first dollar sign, with a space after it.

This site uses Akismet to reduce spam. Learn how your comment data is processed.