Coupling Through Emergent Conservation Laws (Part 8)

joint post with Jonathan Lorand, Blake Pollard, and Maru Sarazola

To wrap up this series, let’s look at an even more elaborate cycle of reactions featuring emergent conservation laws: the citric acid cycle. Here’s a picture of it from Stryer’s textbook Biochemistry:

I’ll warn you right now that we won’t draw any grand conclusions from this example: that’s why we left it out of our paper. Instead we’ll leave you with some questions we don’t know how to answer.

All known aerobic organisms use the citric cycle to convert energy derived from food into other useful forms. This cycle couples an exergonic reaction, the conversion of acetyl-CoA to CoA-SH, to endergonic reactions that produce ATP and a chemical called NADH.

The citric acid cycle can be described at various levels of detail, but at one level it consists of ten reactions:

\begin{array}{rcl} \mathrm{A}_1 + \text{acetyl-CoA} + \mathrm{H}_2\mathrm{O} & \longleftrightarrow & \mathrm{A}_2 + \text{CoA-SH} \\ \\ \mathrm{A}_2 & \longleftrightarrow & \mathrm{A}_3 + \mathrm{H}_2\mathrm{O} \\ \\ \mathrm{A}_3 + \mathrm{H}_2\mathrm{O} & \longleftrightarrow & \mathrm{A}_4 \\ \\ \mathrm{A}_4 + \mathrm{NAD}^+ & \longleftrightarrow & \mathrm{A}_5 + \mathrm{NADH} + \mathrm{H}^+ \\ \\ \mathrm{A}_5 + \mathrm{H}^+ & \longleftrightarrow & \mathrm{A}_6 + \textrm{CO}_2 \\ \\ \mathrm{A}_6 + \mathrm{NAD}^+ + \text{CoA-SH} & \longleftrightarrow & \mathrm{A}_7 + \mathrm{NADH} + \mathrm{H}^+ + \textrm{CO}_2 \\ \\ \mathrm{A}_7 + \mathrm{ADP} + \mathrm{P}_{\mathrm{i}} & \longleftrightarrow & \mathrm{A}_8 + \text{CoA-SH} + \mathrm{ATP} \\ \\ \mathrm{A}_8 + \mathrm{FAD} & \longleftrightarrow & \mathrm{A}_9 + \mathrm{FADH}_2 \\ \\ \mathrm{A}_9 + \mathrm{H}_2\mathrm{O} & \longleftrightarrow & \mathrm{A}_{10} \\ \\ \mathrm{A}_{10} + \mathrm{NAD}^+ & \longleftrightarrow & \mathrm{A}_1 + \mathrm{NADH} + \mathrm{H}^+ \end{array}

Here \mathrm{A}_1, \dots, \mathrm{A}_{10} are abbreviations for species that cycle around, each being transformed into the next. It doesn’t really matter for what we’ll be doing, but in case you’re curious:

• \mathrm{A}_1= oxaloacetate,
• \mathrm{A}_2= citrate,
• \mathrm{A}_3= cis-aconitate,
• \mathrm{A}_4= isocitrate,
• \mathrm{A}_5= oxalosuccinate,
• \mathrm{A}_6= α-ketoglutarate,
• \mathrm{A}_7= succinyl-CoA,
• \mathrm{A}_8= succinate,
• \mathrm{A}_9= fumarate,
• \mathrm{A}_{10}= L-malate.

In reality, the citric acid cycle also involves inflows of reactants such as acetyl-CoA, which is produced by metabolism, as well as outflows of both useful products such as ADP and NADH and waste products such as CO2. Thus, a full analysis requires treating this cycle as an open chemical reaction network, where species flow in and out. However, we can gain some insight just by studying the emergent conservation laws present in this network, ignoring inflows and outflows—so let’s do that!

There are a total of 22 species in the citric acid cycle. There are 10 forward reactions. We can see that their vectors are all linearly independent as follows. Since each reaction turns \mathrm{A}_i into \mathrm{A}_{i+1}, where we count modulo 10, it is easy to see that any nine of the reaction vectors are linearly independent. Whichever one we choose to ‘close the cycle’ could in theory be linearly dependent on the rest. However, it is easy to see that the vector for this reaction

\mathrm{A}_8 + \mathrm{FAD} \longleftrightarrow \mathrm{A}_9 + \mathrm{FADH}_2

is linearly independent from the rest, because only this one involves FAD. So, all 10 reaction vectors are linearly independent, and the stoichiometric subspace has dimension 10.

Since 22 – 10 = 12, there must be 12 linearly independent conserved quantities. Some of these conservation laws are ‘fundamental’, at least by the standards of chemistry. All the species involved are made of 6 different atoms (carbon, hydrogen, oxygen, nitrogen, phosphorus and sulfur), and conservation of charge provides another fundamental conserved quantity, for a total of 7.

(In our example from last time we didn’t keep track of conservation of hydrogen and charge, because both \mathrm{H}^+ and e^- ions are freely available in water… but we studied the citric acid cycle when we were younger, more energetic and less wise, so we kept careful track of hydrogen and charge, and made sure that all the reactions conserved these. So, we’ll have 7 fundamental conserved quantities.)

For example, the conserved quantity

[\text{acetyl-CoA}] + [\text{CoA-SH}] + [\mathrm{A}_7]

arises from the fact that \text{acetyl-CoA}, \text{CoA-SH} and \mathrm{A}_7 contain a single sulfur atom, while none of the other species involved contain sulfur.

Similarly, the conserved quantity

3[\mathrm{ATP}] + 2[\mathrm{ADP}] + [\mathrm{P}_{\mathrm{i}}] + 2[\mathrm{FAD}] +2[\mathrm{FADH}_2]

expresses conservation of phosphorus.

Besides the 7 fundamental conserved quantities, there must also be 5 linearly independent emergent conserved quantities: that is, quantities that are not conserved in every possible chemical reaction, but remain constant in every reaction in the citric acid cycle. We can use these 5 quantities:

• [\mathrm{ATP}] + [\mathrm{ADP}], due to the conservation of adenosine.

• [\mathrm{FAD}] + [\mathrm{FADH}_2], due to conservation of flavin adenine dinucleotide.

• [\mathrm{NAD}^+] + [\mathrm{NADH}], due to conservation of nicotinamide adenine dinucleotide.

• [\mathrm{A}_1] + \cdots + [\mathrm{A}_{10}]. This expresses the fact that in the citric acid cycle each species [\mathrm{A}_i] is transformed to the next, modulo 10.

• [\text{acetyl-CoA}] + [\mathrm{A}_1] + \cdots + [\mathrm{A}_7] + [\text{CoA-SH}]. It can be checked by hand that each reaction in the citric acid cycle conserves this quantity. This expresses the fact that during the first 7 reactions of the citric acid cycle, one molecule of \text{acetyl-CoA} is destroyed and one molecule of \text{CoA-SH} is formed.

Of course, other conserved quantities can be formed as linear combinations of fundamental and emergent conserved quantities, often in nonobvious ways. An example is

3 [\text{acetyl-CoA}] + 3 [\mathrm{A}_2] + 3[\mathrm{A}_3] + 3[\mathrm{A}_4] + 2[\mathrm{A}_5] +
2[\mathrm{A}_6] + [\mathrm{A}_7] + [\mathrm{A}_8] + [\mathrm{A}_9] + [\mathrm{A}_{10}] + [\mathrm{NADH}]

which expresses the fact that in each turn of the citric acid cycle, one molecule of \text{acetyl-CoA} is destroyed and three of \mathrm{NADH} are formed. It is easier to check by hand that this quantity is conserved than to express it as an explicit linear combination of the 12 conserved quantities we have listed so far.

Finally, we bit you a fond farewell and leave you with this question: what exactly do the 7 emergent conservation laws do? In our previous two examples (ATP hydrolysis and the urea cycle) there were certain undesired reactions involving just the species we listed which were forbidden by the emergent conservation laws. In this case I don’t see any of those. But there are other important processes, involving additional species, that are forbidden. For example, if you let acetyl-CoA sit in water it will ‘hydrolyze’ as follows:

\text{acetyl-CoA} + \mathrm{H}_2\mathrm{O} \longleftrightarrow \text{CoA-SH} + \text{acetate} + \text{H}^+

So, it’s turning into CoA-SH and some other stuff, somewhat as does in the citric acid cycle, but in a way that doesn’t do anything ‘useful’: no ATP or NADH is created in this process. This is one of the things the citric acid cycle tries to prevent.

(Remember, a reaction being ‘forbidden by emergent conservation laws’ doesn’t mean it’s absolutely forbidden. It just means that it happens much more slowly than the catalyzed reactions we are listing in our reaction network.)

Unfortunately acetate and \text{H}^+ aren’t on the list of species we’re considering. We could add them. If we added them, and perhaps other species, could we get a setup where every emergent conservation law could be seen as preventing a specific unwanted reaction that’s chemically allowed?

Ideally the dimension of the space of emergent conservation laws would match the dimension of the space spanned by reaction vectors of unwanted reactions, so ‘everything would be accounted for’. But even in the simpler example of the urea cycle, we didn’t achieve this perfect match.

 

 
The paper:

• John Baez, Jonathan Lorand, Blake S. Pollard and Maru Sarazola,
Biochemical coupling through emergent conservation laws.

The blog series:

• Part 1 – Introduction.

• Part 2 – Review of reaction networks and equilibrium thermodynamics.

• Part 3 – What is coupling?

• Part 4 – Interactions.

• Part 5 – Coupling in quasiequilibrium states.

• Part 6 – Emergent conservation laws.

• Part 7 – The urea cycle.

• Part 8 – The citric acid cycle.

This entry was posted on Tuesday, July 3rd, 2018 at 12:00 pm and is filed under biology, chemistry, information and entropy, networks. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

12 Responses to Coupling Through Emergent Conservation Laws (Part 8)

  1. Peter Cudmore says:
    3 July, 2018 at 11:47 pm

    Hi John, Jonathan, Blake and Maru.

    Thanks for the insightful series of posts.

    You might be interested in reading some of Robert Alberty’s work. I think in particular his article “Calculation of Equilibrium Compositions of Large Systems of Biochemical Reactions” is relevant to both accounting for ions (which he handles by assuming constant pH, and transforming the ions out), and emergent conservation laws.

    If you will pardon my blatant advertising, you might also be interested in some of the work going on at our lab regarding bond graph models of biochemical systems.

    Best,
    Pete

    Reply
    • Ishi Crew says:
      7 July, 2018 at 1:51 pm

      I looked at your web page. Your ‘bond-graph-clinic’ pdfs I found very good –i’ve seen some or many of the formulas in other forms in statistical mechanics, theoretical chemistry and biology.
      Those would be fine tutorials/classes.

      I never had time, competency or discipline to master the details though I had heard of previous applications by Oster, Katchalsky and a precursor–G. Kron. (Most people would say I need another kind of clinic–and i agree, except not the kind they think i need.) Since i could never understand ‘electricity and magnetism’ electrical circuits confuse me. I just like simple signed and labeled graphs–maybe its like music–some like rock, or classical, or jazz, or hiphop though they all overlap.

      My own interest has been trying to reduce all these into ‘one equation’, but I can’t do it. There are papers which do try to do this.

      I was interested you use GitHub–something i only recently heard about because another group i’m slightly involved with uses that for basically ‘social enterprise startups’ (i.e. help people in areas which have few resources or education) set up their own small permaculture communities—gardens for food, little libraries, a computer cafe (since most people can’t afford to buy one so they buy them collectively and share them at the cafe) , help people get a smartphone, etc.

      Anyway, just saying your pdf lectures look good.

      Reply
  2. Nikolay Yakovlev says:
    4 July, 2018 at 4:07 am

    Hi John,
    What are the hidden symmetries behind emergent conservation laws?

    Reply
  3. Ishi Crew says:
    5 July, 2018 at 2:56 pm

    Exactly question i had—it appears the article deals with chemical or mass conservation laws, not the kind dealt with in group theory (noether’s theorem).

    Reply
    • John Baez says:
      5 July, 2018 at 4:45 pm

      To be precise, our article deals with emergent conservation laws, which cannot be explained by conservation of things like phosphorus, iron, charge, mass etc. Biological systems evolve to create these new conservation laws for specific purposes—basically, to prevent certain bad things from happening. The idea is explained in the introduction.

      You folks are making me eager to generalize Noether’s theorem to cover chemical rate equations, and I think I know how.

      Reply
      • Ishi Crew says:
        6 July, 2018 at 7:56 pm

        I think I got your explanation in the Introduction to your paper —these laws are sort of macro properties or metastable states .

        (I took biochemistry though have mostly forgotten the details. Basically part of the the idea is trying to simplify a system of many coupled equations by replacing them with a smaller number—‘dimensional reduction’. I tried to simplify your system of 10 reactions by renaming the variables A_i , h20, Co2 etc.–i find that dizzying (similar to physics convention where you set all fundamental constants equal to 1=h=c=k …).)

        I think H Haken’s ‘order parameter’ (and his ‘slaving principle’ ) as well as I Prigogine’s ‘dissipative structures’ are similar ideas. A random google finds https://arxiv.org/abs/1712.02375 –another kind of emergent conservation law.

        There was also an example in your applied CT course which i plan to look at again which referred to ‘efficient markets’ (or open and closed systems) related to this but i forget which lecture and the exact example, tho i can probably find it. (Had a question in it and i wanted to know the answer.

        Anyway this is all interesting tho i don’t have much time for it.

        Reply
  4. Bruce Smith says:
    5 July, 2018 at 8:32 pm

    All the species involved are made of 6 different atoms (carbon, hydrogen, oxygen, nitrogen, phosphorus and sulfur), and conservation of charge provides another fundamental conserved quantity, for a total of 7.

    (You probably know this, but: In general, the conversation laws due to numbers of atoms of each element might be less than the number of involved elements, if the species involved, treated as vectors in the space of the number of atoms of each element, are not linearly independent. Trivial example: if there were two species, XY and XXYY, then the laws “X is conserved” and “Y is conserved” would be equivalent.)

    Reply
    • John Baez says:
      5 July, 2018 at 9:55 pm

      Good point. For the urea cycle we did a little computer calculation to check that all our conserved quantities, fundamental and emergent, were linearly independent. We didn’t do that here, mainly because this example isn’t going into our paper. If we did, we’d take a certain 12 × 22 matrix and show all 12 rows were linearly independent. We did a similar computation for the urea cycle that appears in our paper.

      There must exist 12 linearly independent conserved quantities for the citric acid cycle, since there are 22 species and 10 linearly independent reactions. So if our 12 conserved quantities turned out not to be linearly independent, there would be others that were, and we’d have to find them.

      That too, of course, could be done by computer. But I learned a lot by finding conserved quantities by hand: it turns out you can visually identify a bunch just by looking at the reaction network, and this turns out to be connected to (some very simple bits of) cohomology theory.

      Reply
  5. Toby Bartels says:
    6 July, 2018 at 11:33 am

    There are a few problems with this example. I submitted a comment earlier, but I don't know what happened to it; I never got the email to confirm that I want notifications of further comments. Hopefully I'll remember everything.

    To begin with, the 23 species here, not 22. At some point, you say that H+ isn't included among the species, which would reduce the number to 22, but thay would also mean that you can't include conservation of hydrogen and charge among the conservation laws. (You could still include the difference of those two laws, however.) So we're short a conservation law.

    Also, the law you claim ‘expresses the fact that during the first 7 reactions of the citric acid cycle, one molecule of acetyl-CoA is destroyed and one molecule of CoA-SH is formed’ is wrong; two of the reactions violate it. The fact that it's claimed to express is true, however; unfortunately, the law that actually expresses this (following the pattern set by the immediately following example) is the same as the law of conservation of sulfur. So now we're short two laws.

    The immediately following example might be independent now; I haven't checked. Nor have I tried to come up with a law by direct calculation. In principle, these calculations done, but they don't sound fun.

    I do know one thing, however: the conservation law that we need to add if we include acetate among the species. Unfortunately, it’s a boring law: conservation of acetate.

    Reply
    • Toby Bartels says:
      6 July, 2018 at 11:35 am

      Oops, one other thing: the H+ on the A7 side of the reaction between A6 and A7 shouldn't be there. (Also, there are several typos in my previous comment.)

      Reply
    • John Baez says:
      6 July, 2018 at 7:48 pm

      Toby wrote:

      Unfortunately, it’s a boring law: conservation of acetate.

      Yeah. This is one reason we didn’t include this example in our paper!

      In the urea cycle example, which we wound up using instead, we decided not to count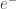 e^- and \mathrm{H}^+ as species. But in our work on the citric acid, we painstakingly made sure all reactions conserved charge and hydrogen, which was hard because (as noted elsewhere on this thread), most online references don’t get these details right.

      It sounds like I didn’t manage to count the species correctly, though.

      Anyway, thanks for the corrections. It would be nice to do something with this example someday; I’m just not sure what.

      Reply

You can use Markdown or HTML in your comments. You can also use LaTeX, like this: $latex E = m c^2 $. The word 'latex' comes right after the first dollar sign, with a space after it.

This site uses Akismet to reduce spam. Learn how your comment data is processed.