Cosma Shalizi wrote a great review of this book:
• David Easley and Jon Kleinberg, Networks, Crowds and Markets: Reasoning about a Highly Connected World, Cambridge University Press, Cambridge, 2010.
Apparently this is one of the first systematic textbooks on network science, which Shalizi defines as:
the study of networks of semiautonomous but interdependent units and of the way those networks shape both the behavior of individuals and the large-scale patterns that emerge from small-scale interactions.
This is not quite the same as what I’ve been calling network theory, but I’d like to see how they fit together.
Shalizi’s review includes a great putdown, not of the book’s authors, but of the limitations of a certain concept of ‘rationality’ that’s widely used in economics:
What game theorists somewhat disturbingly call rationality is assumed throughout—in other words, game players are assumed to be hedonistic yet infinitely calculating sociopaths endowed with supernatural computing abilities.
Clearly we have to go beyond these simplifying assumptions. There’s a lot of work being done on this. One important approach is to go out and see what people actually do in various situations. And another is to compare it to what monkeys will do in the same situations!
Monkey money
Here’s a video by Laurie Santos, who has done just that:
First she taught capuchin monkeys how to use money. Then, she discovered that they make the same mistakes with money that people do!
For example, they make different decisions in what mathematically might seem like the same situation, depending on how it’s framed.
Suppose I give you $1000, and then ask which game would you rather play:
1) a game where I give you either $1000 more or nothing more, with equal odds.
2) a game where I always give you $500 more.
Most people prefer game 2), even though the average, or expected amount of money collected is the same in both games. We say such people are risk averse. Someone who loves to gamble might prefer game 1).
Like people, most capuchin monkeys chose game 2), although Santos used grapes rather than money in this particular experiment.
So, like people, it seems monkeys are risk averse. This is not a ‘mistake’: there are good reasons to be risk averse.
On other hand, suppose I give you $2000 — twice as much as before! Feel all those crisp bills… think about all the good stuff you can buy. Now, which game would you rather play:
1′) a game where I either take away $1000 or nothing, with equal odds.
2′) a game where I always take away $500.
Most people prefer game 1′). The strange thing is that mathematically, the overall situation is isomorphic to the previous one. It’s just been framed in a different way. The first situation seems to be about ‘maximizing gains’. The second seems to be about ‘minimizing losses’. In the second situation, people are more likely to accept risk, in the hopes that with some chance they won’t lose anything. This is called loss aversion.
Monkeys, too, prefer game 1′).
This suggests that loss aversion is at least 35 million years old. It’s survived a long process of evolution! To me that suggests that while ‘irrational’, it’s probably a useful heuristic in most situations that commonly arise in primate societies.
Laurie Santos has a slightly different take on it. She says:
It was Camus who once said that man is the only species who refused to be what he really is. But the irony is that it might only be by recognizing our limitations that we can really actually overcome them.
Does economics elude mathematical reasoning?
For yet another approach the enormous project of reconciling economics to the reality of human behavior, see:
• Yanis Varoufakis, Foundations of Economics: A beginner’s companion, Routledge, London, 1998.
• Yanis Varoufakis, Joseph Halevi and Nicholas J. Theocarakis, Modern Political Economics: Making Sense of the Post-2008 World, Routledge, London, 2011.
For the introduction of the first book go here. The second is described on the Routledge website:
The book is divided into two parts. The first part delves into every major economic theory, from Aristotle to the present, with a determination to discover clues of what went wrong in 2008. The main finding is that all economic theory is inherently flawed. Any system of ideas whose purpose is to describe capitalism in mathematical or engineering terms leads to inevitable logical inconsistency; an inherent error that stands between us and a decent grasp of capitalist reality. The only scientific truth about capitalism is its radical indeterminacy, a condition which makes it impossible to use science’s tools (e.g. calculus and statistics) to second-guess it. The second part casts an attentive eye on the post-war era; on the breeding ground of the Crash of 2008. It distinguishes between two major post-war phases: The Global Plan (1947-1971) and the Global Minotaur (1971-2008).
The emphasis is mine here, not because I’m sure it’s true, but because of how important it could be. It seems quite plausible to me. People seem able to squirm out of any mathematical framework we set up to describe them, short of the laws of physics. Still, I’d like to see the book’s argument. If there’s a ‘logical inconsistency’ in something, I want to actually see it.
You can get a bit more feeling for the second book in a blog post by Varoufakis. Among other things, he makes a point reminiscent of one that Phil Henshaw has repeatedly hammered home here:
Imagine a theorist that tries to explain complex evolving ecosystems by means of engineering models. What would result but incongruity and a mindset bent on misunderstanding the essence of the explanandum; a flight from that which craves explanation?
(By the way: I thank Mike Stay and Miguel Carrión-Álvarez for pointing out some items that appear in this blog entry. They did this on Google Plus. More on that later, maybe.)

Wins and losses are different in everyday life. If you current standard of living is sustainable, wins are a luxury and losses are life threatening. So facing a loss will trigger very different instincts than facing a win :-)
When you pose such puzzles to peoples or monkeys you have to keep in mind that most people don’t think in an abstract way as mathematicians do. Consider this example: You have two kinds of fertilizer, A and B. You know that of 4 trees who got A, three thrived and one died. Of 36 trees that got B, 24 thrived and 12 died. Which fertilizer would you buy?
Many people choose B, because
1) there is obviously more of it or
2) knowing about 36 trees means something, knowing about 4 trees does not mean anything. Let’s say a fifth and sixth tree getting A would have died, then A would be worse than B.
So is choosing A really “irrational”?
Tim wrote:
Right. It’s good for us to have these instincts, but the games I mentioned manipulate those instincts in a way that can only be overcome by the use of reasoning.
This whole business is closely related to the problem of sunk costs.
It would be interesting to ask a statistician, or better yet someone working on ‘decision theory’, what they think the official ‘correct’ answer to your question is.
I presume the correct answer depends on our degree of risk aversion, since we’re more certain that 3/4 of trees will thrive in the latter scenario. If we’re risk-loving, we might focus our attention on the fact that in the former scenario, where there’s more uncertainty, there’s a larger chance that more than 3/4 of trees will survive. If we’re risk averse, we might focus our attention on the fact that in the former scenario there’s also a larger chance that less than 3/4 of trees will survive.
In case anyone is trying to understand what I wrote in the final paragraph above: I misread the puzzle. I thought Tim was giving us a puzzle where the fraction of trees that live is the same in both cases, and only the sample size is different.
I was actually going by your interpretation of the puzzle until I realized that it didn’t agree with Tim’s statement of the problem, which is why I asked for clarification.
There is an interesting result for your version of the puzzle, though, when only the sample size differs.
My previous result found that the “optimal” decision is to choose the fertilizer which maximizes , where
, where  is the number of successes and
is the number of successes and  is the number of trials. We can rewrite this quantity as
is the number of trials. We can rewrite this quantity as  , where
, where  is the sample success rate (equal to the posterior mode in my inference calculation).
is the sample success rate (equal to the posterior mode in my inference calculation).
The question is, given experiments with the same but different
but different  ‘s, which experiment should you prefer? Does it depend on
‘s, which experiment should you prefer? Does it depend on  , or only
, or only  ?
?
If we are to prefer fertilizer 1 to fertilizer 2, we need . A little algebra shows that this holds when
. A little algebra shows that this holds when  .
.
In other words, given two experiments with identical sample success rates, pick the one that has more data supporting that success rate.
A better analogy may be soccer: You win or you lose (let’s forget about draws), but it does not matter if you win scoring one goal or ten goals. So if a team is one goal behind and there are only minutes left, usually all players leave the defense and begin to attack (sometimes including the goal keeper): You either turn the game around or the opposing team scores another goal or two (which does not matter at all).
So the leading team plays it safe while the team that is behind takes all kinds of risks.
What underlying question are you interested in?
Is fertilizer B also supposed to have a 3/4 probability of success (27 thrived and 9 died), so that the question is what should you decide when you have the same apparent probability of success, but a different number of trials? That would assume you made a typo and meant 27 instead of 24.
Or did you intend for fertilizer B to have a lower fraction of successes (2/3) than fertilizer A (3/4), so the question is whether one should choose a more confidently assessed low probability over a more uncertain high probability? That’s more ambiguous since it will depend on how much difference there is between the fraction of successes in the two experiments, as well as on the numbers of trials.
If we assume each tree to be an independent trial, the successes will be Poisson-distributed, so the two fertilisers in the example given are not statistically distinguishable to even one sigma, let alone the conventional 5 % threshold. Given this, a risk-averse person should, canonically, pick the one with the bigger sample: Same expected value, lower variance of the expectation.
The expected value of A (3/4) is better than that of B (2/3), but besides that I think that a statistical analysis like the one you did will show that the samples are too small to be significant. But if there is no way to change this, what would you do?
If there were no way to change the sample size, I would pick the cheaper one if I believed that I needed fertiliser, or go without if the need for fertiliser was marginal. Neither will kill my trees outright, and neither has shown any efficacy above the other (or even convincingly show an effect above doing nothing, but there are stronger priors for the existence of the latter effect than for the former).
If equally priced, I would pick the one that had been tested on the larger sample, given that they are statistically indistinguishable and I prefer the variance of my expected value to be smaller if all else is strictly equal.
This was a test question in Germany for students in ground school, designed to find out if the students are able to calculate ratios and interpret them as probabilities. The solution is supposed to be that
– A has a success rate of 3/4 and
– B has a success rate of 2/3
so that A is the better fertilizer (not a typo). A neutral way to pose the question would be drawing cards from a deck or drawing pebbles out of a sack. But the designer of the question (a professor of pedagogy) chose trees and fertilizers because he assumed that children at the age of 10 would be unable to relate to such an abstract setting. His conclusion of the outcome was that there should be a stronger focus on stochastics earlier on.
My main point is that people usually assume/infer some real world context when they answer such a question. Their answers are rational and make sense given such a context. From this viewpoint it is the artificial situation of the question that is irrational – which is a point that Laurie Santos – I think – tried to make: We are capable to create highly artificial situations where our instincts fail, and only few people who are capable of strict abstraction can survive.
Another example, from the same professor, is the question “there are 99 white pebbles in a sack and one red pebble, how probable is it to pick the red pebble”. Most students answered “tit is impossible”. The author interpreted this as “people are unable to distinguish improbable and impossible”. I think that most students (mis)understood the question and understood this: “is there some systematic way to always pick the red pebble?” or “Would you bet on picking the red pebble?”.
I want to agree strongly with what Tim has been arguing.
The use of these games is to experiment and discover how people (or monkeys, or crows, or …) behave. However, when we say that they are behaving irrationally because they don’t give the answer we first thought of, the tail is wagging the dog.
A better discussion is to try and explain why the behaviour evolved to be that way. We have discussed in other posts the necessity of omitting all but the most salient features. Experiments like these can help to reveal which neglected features weren’t negligible.
It may also mean that modelling of economics. The logical inconsistencies alluded to in the quote arise from infinite recursion: the model itself is part of the system being modelled and if the actors are ‘perfectly rational’ and the model is ‘perfect’, they will all us it. Therefore, at least one of the premises is wrong. However since the first premise is certainly false, there may be hope for the second.
Ok good, I didn’t misunderstand the problem.
It’s fun to work out an official ‘correct’ answer mathematically, as John suggested. Of course, this ends up being a long way of confirming the obvious – and the answer is only as good as the assumptions – but I think it’s interesting anyway. In this case, I’ll work it out by maximizing expected utility in Bayesian decision theory, for one choice of utility function. This dodges the whole risk aversion point, but it opens discussion for how the assumptions might be modified to account for more real-world considerations. Hopefully others can spot whether I’ve made mistakes in the derivations (and I’ve made no typos in the HTML or LaTeX, which I can’t preview).
In Bayesian decision theory, the first thing you do is write down the data-generating process and then compute a posterior distribution for what is unknown.
In this case, we may assume the data-generating process (likelihood function) is a binomial distribution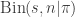 for
for  successes in
successes in  trials, given a probability of success
trials, given a probability of success  . Fertilizer A corresponds to
. Fertilizer A corresponds to 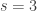 ,
,  and fertilizer B corresponds to
and fertilizer B corresponds to 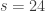 ,
, 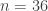 .
.
The probability of success is unknown, and we want to infer its posterior conditional on the data,
is unknown, and we want to infer its posterior conditional on the data,  . To compute a posterior we need to assume a prior on
. To compute a posterior we need to assume a prior on  .
.
It turns out that the Beta distribution is conjugate to a binomial likelihood, meaning that if we assume a Beta distributed prior, the then the posterior is also Beta distributed. If the prior is then the posterior is
then the posterior is
One choice for a prior is a uniform prior on![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) , which corresponds to a
, which corresponds to a 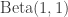 distribution. There are of course other prior choices which will lead to different conclusions. For this prior, the posterior is
distribution. There are of course other prior choices which will lead to different conclusions. For this prior, the posterior is 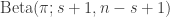 . The posterior mode is
. The posterior mode is 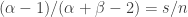 and the posterior mean is
and the posterior mean is
So, what is the inference for fertilizers A and B? I made a graph of the posterior distributions. You can see that the inference for fertilizer B is sharper, as expected, since there is more data. But the inference for fertilizer A tends towards higher success rates, which can be quantified.
Fertilizer A has a posterior mode of 3/4 = 0.75 and B has a mode of 2/3 = 0.667, corresponding to the sample proportions. The mode isn’t the only measure of central tendency we could use. The means are 0.667 for A and 0.658 for B; the medians are 0.686 for A and 0.661 for B. No matter which of the three statistics we choose, fertilizer A looks better than fertilizer B.
But we haven’t really done “decision theory” yet. We’ve just compared point estimators. Actually, we have done a little decision theory, implicitly. It turns out that picking the mean corresponds to the estimator which minimizes the expected squared error in , where “squared error” can be thought of formally as a loss function in decision theory. Picking the median corresponds to minimizing the expected absolute loss, and picking the mode corresponds to minimizing the minimizing the 0-1 loss (where you lose nothing if you guess
, where “squared error” can be thought of formally as a loss function in decision theory. Picking the median corresponds to minimizing the expected absolute loss, and picking the mode corresponds to minimizing the minimizing the 0-1 loss (where you lose nothing if you guess  exactly and lose 1 otherwise).
exactly and lose 1 otherwise).
Still, these don’t really correspond to a decision theoretic view of the problem. We don’t care about the quantity at all, let alone some point estimator of it. We only care about
at all, let alone some point estimator of it. We only care about  indirectly, insofar as it helps us predict something about what the fertilizer will do to new trees. For that, we have to move from the posterior distribution
indirectly, insofar as it helps us predict something about what the fertilizer will do to new trees. For that, we have to move from the posterior distribution  to the predictive distribution
to the predictive distribution
where is a random variable indicating whether a new tree will thrive under treatment. Here I assume that the success of new trees follows the same binomial distribution as in the experimental group.
is a random variable indicating whether a new tree will thrive under treatment. Here I assume that the success of new trees follows the same binomial distribution as in the experimental group.
For a Beta posterior, the predictive distribution is beta-binomial, and the expected number of successes for a new tree is equal to the mean of the Beta distribution for – i.e. the posterior mean we computed before,
– i.e. the posterior mean we computed before,  . If we introduce a utility function such that we are rewarded 1 util for a thriving tree and 0 utils for non-thriving tree, then the expected utility is equal to the expected success rate. Therefore, under these assumptions, we should choose the fertilizer that maximizes the quantity
. If we introduce a utility function such that we are rewarded 1 util for a thriving tree and 0 utils for non-thriving tree, then the expected utility is equal to the expected success rate. Therefore, under these assumptions, we should choose the fertilizer that maximizes the quantity  , which, as we’ve seen, favors fertilizer A (0.667) over fertilizer B (0.658).
, which, as we’ve seen, favors fertilizer A (0.667) over fertilizer B (0.658).
An interesting mathematical question is, does this ever work out to a “non-obvious” conclusion? That is, if fertilizer A has a sample success rate which is greater than fertilizer B’s sample success rate, but expected utility maximization prefers fertilizer B? Mathematically, we’re looking for a set such that
such that 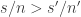 but
but  . (Also there are obvious constraints on
. (Also there are obvious constraints on  and
and 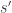 .) The answer is yes. For example, if fertilizer A has 4 of 5 successes while fertilizer B has 7 of 9 successes.
.) The answer is yes. For example, if fertilizer A has 4 of 5 successes while fertilizer B has 7 of 9 successes.
As I said earlier, all of this misses the point you initially raised, which is that there might be reasons to prefer fertilizer B with a more certain quantification of success. This leads to the question of how the above calculations may be altered to take these considerations into account.
Wonderful work, Nathan! I wish I understood it more fully. I’m not at all comfortable with the beta distribution or the concept of conjugate prior.
It’s amazing what German elementary school students are expected to know.
I’m not really that familiar with the theory of beta distributions, either. I just got the analytic results out of a textbook.
As for conjugate priors, they’re purely for convenience. Statisticians realized that for certain likelihood functions, if you choose the prior to have a particular functional form, then the posterior will have the same functional form. This is what a “conjugate” prior is: one where the prior and posterior come from the same family of distributions (given a likelihood function).
This does two things for you: first, it gives a posterior in some simple closed form that you can work with analytically. Second, since the posterior and the prior have the same functional form, it makes it more obvious how “Bayesian updating with data” works: you end up with the same kind of distribution you started out with, except now some of its parameters have been “updated with data”. You can keep updating sequentially with more data and you keep getting the same kind of distribution, except with its parameters changing to focus the distribution on the “truth”.
In my research, I generally do all my inference via MCMC sampling, where it doesn’t matter whether your prior happens to have some nice form. So I don’t normally use conjugate priors. (In fact, sometimes it’s a hindrance to work with conjugate priors if you have really informative prior information, because then you have to worry whether that family of distributions is capable of reflecting your prior knowledge.)
In the example above, what I really wanted was an analytic posterior for a uniform prior. It turns out that the beta conjugate prior for the binomial likelihood has the uniform distribution as a special case, meaning that the posterior has a nice analytic form in the beta family. So that worked out.
The use of “rational” in economics is a pet peeve of mine, because it’s an emotionally loaded term used to describe beings who consider “the things economists currently model”, which is both increasing over time (so what a “rational actor” is supposed to do in a given case is slowly changing) and still neglects things that seem likely to be driving forces in building the human brain.
Regarding the difficulties of using statistics in modelling capitalism, I don’t know about inherent contradictions. I suspect that most human beings, myself included, have “views” which naturally operate in different areas and if “extended out until they meet” would turn out to be inconsistent. (The famous examples of inconsistent “utility functions” for very simple mathematical games is an example of this.) However, I’m not sure that it’s a fatal problem in practice.
What strikes me as more immediate is that I’ve skimmed over lots of physics/mathematics based models but have generally decided against reading them in detail. This is for the simple reason that they tend to do an awful lot of “lets assume that x has the form a” rather than taking some experimental data and doing a (non-parametric) model fit to it. This gives me the uneasy feeling that the models are written down more because the author thinks they’ll be nice (in the sense of tractable either analytically or computationally) than because he/she thinks they’re accurate abstractions of the world. (In physics the two seem to coincide a lot of the time so the issue is less pressing.) Maybe in the future there’ll be a wave of “massive computer-simulating behavioural economists”.
The question is not whether humans are “hedonistic yet infinitely calculating sociopaths”, for they certainly are not. The real questions is whether such assumption is justified for studying those kinds of topics that economists are interested in. And the only way to find out is to try and build models based on it, derive their implications and compare them with observed data.
Having done that, it really turns out that standard expected utility theory is sometimes contradicted. However, those violations of expected utility are well known in economics, and there have been attempts to deal with them. For example, Kahneman & Tversky’s prospect theory, one of the first approaches, postulates that people perceive probabilities of outcomes in a nonlinear way, with greater emphasis on “losses”, which can explain framing and loss aversion biases. Since then, there has been further research on theoretical modeling of preferences under uncertainty (see e.g. here or here), as well as huge amount of experimental work documenting variety of behavioral biases. And Kahneman, together with Vernon Smith, later got Nobel Prize for work on behavioral and experimental economics. So if evidence of “irrationality” is supposed to be a criticism of economic theories, economists are already well aware of it.
I also tried to read Varofakis’ blog you referred to, but was quickly discouraged by all the rhetorics and lack of substance. Anyway, as Samuelson (citing Willard Gibbs) wrote, mathematics is a language – it may be more suitable for some things than other, but in principle, what we express with mathematics could be expressed with words and vice versa. Also, criticizing specific applications of mathematics in economic theory doesn’t prove that there are no such (correct) applications to be found in the future. For those reasons, I find such broad dismissals of mathematics unpersuasive and/or ideologically motivated, and this seems to be just such case.
Ivan wrote:
I’m afraid I too was a bit put off – in particular where he said:
Being a mathematician, when someone claims something ‘leads to an inevitable logical inconsistency’, I want to see some framework where some clearly stated assumptions lead to a contradiction. I didn’t see anything like that in the blog article, and I can only wonder what’s in the book.
I’m sure many of them are, but has this realization been thoroughly integrated into the heart of the subject? I doubt it. I bet there’s still a lot of work that’s based on the assumption that people are rational utility-maximizing agents.
I guess you’ll say we need to do that work to figure out when that assumption works and when it doesn’t.
By the way, I’m glad you’re sticking up for economics on this blog. No matter what the problems are with standard economic thinking, there’s no way to advance beyond it without knowing it… and I don’t claim to know it well.
I agree that in principle that what we express with mathematics could be expressed with words, but I disagree with the ‘vice versa’. Barring revolutionary developments which may come about someday but certainly aren’t here now, we couldn’t be having this conversation in the language of mathematics.
I think most interesting things in life elude the grasp of mathematics.
John Baez:
That is a good question, which I kind of avoided, as I don’t feel qualified enough to answer it. There are lot of subfields in economics, and probably only someone who follows research frontier in particular field could say how much behavioral biases matter and how are they incorporated into applied work. I am somewhat interested in macroeconomics, and there exist models with “exotic” preferences, but as is always the case with macroeconomics, data are limited and it can be hard to distinguish between different models and explanations.
Yes, that’s true :) What I believe Samuelson meant (and I should have said more clearly) is that if you have an idea about some economic phenomena, it should be possible to write a formal model that captures, or illustrates the idea. And if you have formal model, you should be able to express its main implications and insights verbally.
But that is not necessarily a productive use of your time. For instance, you can construct an elaborate mathematical model of asset bubbles… but I doubt that it will add much explanatory or predictive value over Galbraith’s The Great Crash of 1929. When economic behaviour is driven by mass psychology and other sociological phenomena that have not been (and possibly can not be) captured in mathematical formalism, such formalism should be used with some care as to applicability.
You can try to construct a flow-of-funds model to tell you the rate of new equity infusion and/or lowering of margin requirements will be required to sustain the bubble over one, three or six months, but you’re likely to end up with a number of unobserved or unobservable variables, as well as plain old fudge factors. And it is unlikely to give you sufficient advance warning to be able to withdraw before the crash. And regulatory action against bubbles is perfectly straightforward and does not require sophisticated cause-and-effect models, so it’s a curiosity in that realm as well.
The problem with economics is not that it uses mathematics. It is that it uses retarded mathematics. Equilibrium based economic analysis is an intellectual cul-de-sac, and you cannot get out of it simply by grafting on some bastard dynamics and game theory. You have to do proper, stock-flow consistent dynamic modeling if you want to say anything that is both interesting and true at the same time.
You also have to accept the fact that you have to go from macro to micro rather than the other way around, because the macroeconomic world is more easily observable than the microeconomic. Quite simply, “inadequate microfoundations” is not an acceptable scientific argument against a macroeconomic model that is consistent with observed reality. Whereas “inconsistent with observable macroeconomic reality” is a perfectly valid argument against a microeconomic model.
Put these two simple facts together, and you can toss pretty much the whole Marginalist school.
(Incidentally, I have yet to meet a utility function that had any explanatory or predictive power – utility “theory” is a post-hoc rationalisation of observed behaviour that can be jettisoned without loss of generality. That is, when it isn’t Jesuit logic in pursuit of a predetermined conclusion, such as in the case of Friedman’s “long-run” Phillips curve.)
Fascinating stuff! But let’s try to avoid insulting language like ‘retarded’. Insults, even when directed against abstractions like ‘economics’, tend to make people segregate into warring packs. I’d rather make it easy for people to communicate and change their minds without it counting as ‘defeat’.
I’m afraid some of this my fault. What I’d really like to do is coax economists to do better, not castigate them. But I get so frustrated by the economic situation of the world as a whole that I sometimes slip into treating economists as a convenient scapegoat.
Jakob Stenfalk:
One wonders, what is this retarded mathematics? Are stochastic dynamic programming, Ito calculus or Kakutani fixed point theorem retarded only when used by economists, or should engineers and physicists worry as well?
More seriously, I’m not familiar with stock-flow modeling (whatever that is), and since you don’t provide any arguments or references, there is not much I can say. But the claim that macroeconomic world is more easily observable than microeconomic is certainly not correct – data on macro aggregates are limited, go back at most a few decades, and even their construction is not so simple (e.g. how do you really measure inflation?). Compare this with empirical micro studies, which nowadays often use large databases on individual or firm level containing (at least) thousands of observations, and the difference is clear (this of course doesn’t mean that micro-econometrics is easy).
The debate about microfoundations has been of course going on for decades, so I’m not expecting to persuade anyone in a short comment like this. However, as Lucas’ critique tells us, it is possible to have model which is consistent with observed data, yet is useless for evaluating policy counterfactuals (think of some purely statistical, reduced-form time series model), so fit to data cannot be the only criterion. And to say that we don’t need to think about how the aggregate behavior is derived from individual behavior sounds strangely anti-scientific – it’s as if physicists said that they’re not interested in atoms and molecules because the only thing that matters are macroscopic laws. It may turn out that studying microfoundations will not bring much insight into macroeconomics, but that’s far from being obvious.
The problem with explanations like these is that they can easily morph into meaningless tautologies: “markets have gone up (down) because investors are optimistic (pessimistic)” kind of thing. It’s certainly more fruitful if economists first try to find explanations within their field before giving up and leaving the task to others.
General equilibrium models. If you see someone using “equilibrium” and “stochastic” in the same sentence – let alone the same title – you should run, not walk, away from that person.
Mitchell has a primer on stock-flow consistency and the related flow-of-funds models here. The tl;dr version is that it’s a model that properly incorporates the most elementary accounting identities of modern monetary economies. Neoclassical general equilibrium models (both fresh- and saltwater) fail to do this, and as a result are little more than computationally expensive nonsense.
Simple: You pick a basket of goods and measure its price change. How you pick that basket is a political choice, which no amount of microfoundations will permit you to elude. Though they may permit you to obfuscate it.
But for most practical purposes a chain index will work just fine. Knowing the precise rate of inflation is not very important to the material provisioning of society, so some leeway in measuring it is perfectly permissible.
Obviously. But that is an argument for forward-looking models with predictive power, not for microfoundations per se.
To argue that it makes the case for microfoundations is broadly equivalent to arguing that the existence of the Ptolemaic model of planetary motion argues for attempting to derive Kepler’s laws from quantum mechanical ab initio calculations.
You will not win a Nobel Prize that way. Maybe a Swedish Bank prize, but that is not quite the same thing.
I would like to take this opportunity to remind you that the laws of physics have been discovered from macro to micro: The earliest human activity broadly recognisable as modern physics is the study of planetary motion. From there it proceeded downward to ever smaller components.
And indeed if you were to come up with a brilliant new unified theory of quantum gravity, it would be rejected in a heartbeat if it failed to conform to Newton’s laws in the classical limit (where the speed of light is set to infinity and the Planck constant to zero for all objects with non-zero rest mass).
You have broadly similar processes in biology (from Linnean zoology through Darwinian evolution through Mendelian genetics to the modern synthesis), the other natural science whose history I know well enough to pass comment.
There may be an epistemological or practical case for starting with microfoundations and attempting to derive macroeconomic relationships, as opposed to starting with macroeconomic relationships and using them as a litmus test for the validity of any microeconomic model. But if there is, it will not be found in the natural sciences.
Nor will it be found in the record of abject and utter failure that Marginalist microfoundation economics has amassed over the 20th century. An incomplete list of which includes the Great Depression; the last thirty years of thirdworldisation of the first world; the collapse of the SE Asian and Latin American dollar- and yen pegs; the ongoing collapse of the Eurozone under the weight of German neo-classical policy prescriptions; the Russian disaster on Rubin’s and Summers’ watch; the IMF’s record for turning disaster into catastrophe with almost mathematical inevitability; and so on and so forth.
It is no coincidence that the three decades where the West grew the most, the fastest and with the fewest hiccoughs were the three postwar decades when Walrasian microfoundations were thrown under the bus.
That is actually far from a meaningless statement. It tells you that the market is currently believed to be driven by sentiments rather than fundamentals. That is true only for some markets some of the time. And indeed there are markets (such as the pre-Lower 48 peak crude oil market) where it cannot be true.
Further, investigation into the fundamentals is poorly served by marginal utility models, and better served by examining the engineering constraints, the state of physical resources, the available men and machines, the industry’s debt load, the regulatory environment and so on.
Ivan wrote
I’m actually quite interested in this for various reasons. Could you recommend a paper (downloadable by someone without univ affiliation) that you think is a good example of data gathering and rigorous model testing in economics for me to read? (I’ve currently been given a stack of econometrics textbooks to read and, perhaps because they’re textbooks, statements like “a Wiener process is appropriate here” don’t seem particularly well supported with evidence and testing. (Note the distinction between saying that the statement is wrong and saying the presented evidence doesn’t seem like strong support.) I’d like to see how things work out in full-on economics research.)
Jakob,
It would be a lot more helpful to see a toy example of a CGE which fails on some problem for some intuitive reason, along with an example of a stock-flow model of the same problem which succeeds. As it is, I don’t get much out of your posts other than “CGE models are stupid”.
Deflation. General equilibrium models pretend that this has no long-run effect on real variables, due to the assumption of long-run money neutrality.
A flow of funds model will tell you immediately that deflation leads to more bankruptcies among productive firms as their nominally fixed debt burden increases. And elementary institutional analysis will tell you that letting firms that would have been sound under full employment go bust has a deleterious effect on long-run growth.
Another example centred around long-run money neutrality: Dynamic flow-of-funds models will tell you that inflation can be too low, because productive firms have to meet fixed nominal obligations, which creates a downward rigidity in nominal price and attempts to force your way past this are not without costs (in the US case over the last business cycle, the cost has been that real growth has flatlined – median real family income is about where it was ten years ago and median hourly income is down).
Jakob Stenfalk:
But that is also transitory effect, so it’s not fair to invoke money-neutrality. Or are nominal debts of firms supposed to be fixed in the long run, regardless of inflation/deflation? That wouldn’t make much sense – firms choose debt endogenously, and if all prices double, nominal debt will eventually double as well.
Without arguing how exactly has microfounded macreconomics caused all these events, such accusation is meaningless. After all, we don’t blame meteorologists every time there is a tornado, or geophysicists when there is an earthquake. I expect that you will have problems presenting such arguments, since microfounded macro (under which I mean dynamical general equilibrium models) hasn’t really had that much influence over government policy so far. And how could the concept of general equilibrium cause Great Depression, which happened at least two decades before its introduction, seems a bit mysterious.
DavidTweed:
I’m still a graduate student so I don’t feel much of an authority on what is good and what is not :) but I can try. Probably the most important issue in empirical research is to have good identification – that is to convince that what you are estimating is actually a causal effect, not just correlation. Typically this may involve instrumental variable estimation, i.e. finding a variable that causes exogenous variation in your explanatory variable.
For example, Angrist (1990) estimates effect of military service on earnings using Vietnam draft lottery as an instrument (those with lower numbers were more likely to serve). Acemoglu, Johnson & Robinson (2001) estimate effect of institutions on economic growth using historical data on European settler’s mortality as instrument for institutions in colonized countries (higher mortality meant more “extractive” colonization policy and worse institutions). Or, switching to macroeconomics, Gali (1990) uses a structural vector autoregression model, assuming that only technology shocks have long-term impact on labor productivity, to show that conditional correlation between technology shocks and hours worked is negative (which contradicts real business cycle models like those of Kydland & Prescott).
Assumptions behind identification (e.g. that lottery numbers had no impact on earnings other than through military service, or about long term impact of different macroeconomic shocks) are typically discussed extensively, while other, technical assumptions (e.g. linear functional form) are usually discussed less thoroughly, since they are commonly used (if you had to discuss every assumption you make in detail, papers would get really long and boring quite fast). I’m not sure if this helps, or if those papers could be considered flawless, but at least they are quite well known and cited.
You are now assuming your conclusion.
Ceteris paribus, yes. But that is beside the point. Different rates of inflation have the following long-run effects that are contrary to the assumption of money neutrality:
1) Lower real interest rate on liabilities (since the central bank can fix the nominal rate), which permits investment to crowd out consumption. This is normally desirable in terms of long-run growth (per most simple endogenous-growth Solow models).
2) Easier price adjustment, as discussed elsewhere in this thread.
3) Reduces the power of bankers relative to industrial firms and organised labour. This is normally desirable in terms of long-run growth.
4) Reduction in the magnitude of the business cycle by reducing the duration and extent of periodic deleveraging, which has a demonstrated positive effect on long-run growth.
5) If done to excess, dollarisation of your economy and consequent loss of economic sovereignty (which has a negative effect).
As long as you can avoid #5, and as long as you can float your currency, inflation is good for you. Unless you happen to be a banker, in which case my heart bleeds for you.
Let’s see.
They argue that balanced sovereign budgets is a good idea. This is an absolute catastrophe, because the only way other than sovereign deficits you can create new money is by having the (central) bank(s) assume equity risk (no, open market operations in existing sovereign bonds do not count, because sovereign bonds are, when you do your accounting properly, functionally identical to M0, except that they typically pay a subsidy to the holder).
Which tends to blow up your financial system every once in a while. In innovative and interesting ways that are, however, best observed at some distance.
They argue that there is such a thing as a “natural rate of unemployment” which is different from (and conveniently much larger than) frictional unemployment. Historical unemployment and vacancy data does not support the existence of such a beast, but it is none the less used to argue for demonstrably failed economic policies (labour market “flexibility,” union-busting, suppressing aggregate demand, etc.).
Inflation targeting: A very common policy recommendation, which has been a complete catastrophe everywhere it has been implemented, because it prevents use of fiscal policy and the central bank for proper industrial planning and financial stability functions (such as import substitution or defending against currency carry trades).
Related to: Central bank independence. Which is really nothing more than a paper thin disguise for replacing parliamentary oversight of a central policymaking institution with bankster-friendly cronies.
All of these are justified – when they are justified at all – on the basis of microeconomic arguments. Except central bank independence, which is typically justified explicitly on the grounds that making the money markets democratically accountable is undesirable.
Because classical marginalist economics is based explicitly on classical microfoundations, and modern microfoundations are classical microfoundations gussied up in a very expensive cheap suit. Every fallacy Keynes debunked in classical microeconomics is still found in neoclassical micro.
Jakob Stenfalk:
In the long run steady-state, nominal rate = real rate + inflation (Fisher equation). So unless monetary policy influences long run real interest rate (how?), inflation will not lead to more investment and growth, but will simply adjust nominal rate. If prosperity could be achieved by printing money, why we all aren’t already rich?
Same goes for other effects – why should they persist in the long run? There are plenty of mainstream models where money matters in the short-, but not long-run (e.g. standard New-Keynesian models used by central banks). If you are claiming that money is not neutral in the long run, then I think it’s up to you to explain why (otherwise you would be just assuming the conclusion, right?).
Re: sovereign debt, in reality many countries don’t have the luxury of issuing debt in their own currency (see: Greece), so saying “you can always just inflate your debt away” is not very helpful.
I’m not convinced by your assertions, but I guess that would require even longer discussion and we have hijacked this thread enough – let’s just agree to disagree.
That is an ex post identity, not an ex ante operational constraint.
Under a modern central banking system, the nominal interest rate on liabilities is the central bank rate plus private bank overhead. That overhead depends slower than linearly on inflation.
(The trick is that a modern central banking system breaks the arbitrage relation between risk-free return on debt and equity because the central bank does not (permit private banks to) take equity risk on their loan portfolio. In an open economy it gets a little more involved because you have to defend against carry trades as well, but it is perfectly possible to do so without restricting capital mobility.)
Of course, if you follow a Taylor rule you can make nominal interest rates track inflation. But then you are needlessly and uselessly crippling yourself.
See, this is the sort of facile nonsense that passes for neoclassical economics. Printing money does not magically make society richer, but a healthy rate of inflation changes the power relationships between holders of unproductive money and holders of productive capital in beneficial ways.
That is a policy choice, not an operational necessity.
In the Greek case, it is a political decision on part of the ECB to not do its job as a central bank and print unlimited money on demand for countercyclical fiscal policy to maintain full employment.
The problem with financial prediction is the feedback loops. In the natural sciences the fundamental laws can be safely assumed to hold whether or not we have described them yet. This is not true in economics (or any of the social sciences). Widespread knowledge of a particular economic model will in general influence the behaviour of the economic actors being studied, leading to deviations from the model. To be generally applicable, any economic theory must therefore model the consequences of its own existence. This kind of logical recursion is reminiscent of the problems in Hilbert’s grand project, and I think the authors are hinting at an analogous incompleteness theorem.
Hey,
This was interesting, though I found her talk to be a bit rhetorical in dividing “us thinkers” from the whelps who robbed us in 2008.
I think we should just move on and create the economic theory that is due in our time. We have to base all the calculations and reasoning on networks of process. We know that all wealth comes from the processing of object to object or state to state as in information processing or chemical processing. Let’s use the string diagrams in the dagger compact categories and on that foundation, provide tools of analysis that reach up, in complexity, all the way to markets. The people reading this blog are the ones who understand the mathematics. Some of us have a good grasp as to how we can have an entire theory of economics. Let’s just do this.
I realize this is a huge conceptual problem, and maybe some of us are afraid to take a tentative step for fear that our gropings will just attract derision. What are the major roadblocks? Clearly we have the canvas of the diagrammatic calculus as the networks of processing we see in all economies. These networks are understood as abstractions of real physics (quantum operations and concurrent composition), so there is a good basis. That is enough for a first, very important paper. What would be the next step? How would we then make the idea have most traction amongst working and young thinkers.
Needless to say, I’d like to reformulate economics in terms of category theory if I thought I had the foggiest clue as to how.
I think category theory is great for formalizing the math of networks of flows, but I’ve been doing this for systems vastly simpler than economic ones: first electrical circuits, and then stochastic Petri nets (which are good for desic There are lots of other types of networks worth tackling. Perhaps I’m getting old and overly cautious, but my plan is gather a bunch of grad students and maybe postdocs when I return to U.C. Riverside in the fall of 2012, and work towards a general formalism for networked systems by tackling one type after another. Real-world economics and real-world biology would be the holy grail, but I have no great confidence that I’ll get that far.
If you want to join in, that would be great.
I would love to join. I think it is a very honorable endeavor. Yes, real world economics is the holy grail. I tend to overlook the incredible difficulties that would inevitably come, out of, perhaps, the same kind of urgency that every commenter here feels towards the state of our planet.
The monetary economy is a directed network in which the nodes are economic entities and the arrows are credit relations between them. The arrow tips are called assets and the ends are called liabilities. At the nodes you have balance sheets, and cash flow statements.
Credit relations are intertemporal – the basic one is the commitment today to exchange a certain asset at a future date – this shows up as an asset on the recipient’s balance sheet and a liability on the payer’s.
Credit relations can be tradeable or not. If they are “bearer documents” they are tradeable, if they are personal documents they are not. An IOU where I say “I will pay John Baez the amount X” and “I will pay the bearer the amount X” are vastly different instruments, because John Baez can sell the second one to a third party for Y (or in exchange for another asset), but the first one can not be sold.
Some credit relations are explicitly “contingent” on some external event. They are all implicitly contingent on willingness and ability to pay.
Neither the set of nodes nor the set of edges in this network is constant in time.
Categorize this!
Migeruet wrote:
This sort of structure reminds me a bit of the pi calculus: a formalism for modelling situations in computer science where different agents are sending messages to each other. The number of agents, and which ones are connected to which, may change with time.
It’s not the same, but it’s similar. I found the pi calculus very hard to understand at first. I guess I still do. Luckily, my student Mike Stay is setting the pi calculus in a clear mathematical framework. So, perhaps some of his work can be reused here.
John,
A network theory of economics cast in a different mathematical language (i.e. category theory) would be immensely fruitful. I am an economist and find the current state of economics as a science disgraceful.
Rationality is I think a sub-issue once you embed the agents and their relations in dynamic evolving networks. A hyper-rational agent could not even reach her simple rational goal in a dynamic network (links being formed and severed pairwise, one by one or via coalition). S. Goyal’s book, Connections, tells all.
However, a self-interested agent or an organization or even a bunch of agents like (firms+politicians+military) can partially achieve higher benefits by a threat of leaving the network. Private and social welfare almost always diverge. The experiments recently take into account of the significance of network topography in behavioral economics.
The conventional neoclassical economics, even if it could use the frontier math, would be flawed. It assumes either in a connected network (as in General Equilibrium theory) or an empty of a very sparse networks (such as buyer-seller or star-networks).
Jason Potts’ book (http://books.google.com/books?id=xDwfIY3NSVUC&printsec=frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false) is a valuable attempt; but I suspect it can give the clues for your category/network theory of economics.
We have a huge mountain to climb. Apart from creating a relevant language for economics and model a dynamic evolutionary network economics, we have to also persuade the many believers in the trade that the assets they possess (the method and the modeling tools of conventional economics) value much less than they think (what Kahneman and Tversky call endowment bias).
I would love to make some progress on this! Thanks for the hints! So far I’m tackling much simpler systems, like chemical reactions: here we have a bunch of molecules blundering around randomly and interacting in various different ways with various different probabilities when they bump into each other. It’s natural to hope that this could be a step towards modelling the interaction of more ‘goal-oriented’ agents, but I think of it as a very small step.
I was thinking about the efficient market hypothesis last night and realized how comonoids are relevant again.
Suppose you are in a board room meeting and there are ten people sitting around the table. Everyone is waiting for the report which I am about to bring into the room. I have eleven copies of the report. Upon entering the room, I give exactly one report to each of the participants, and I take the last one. The reports sit in front of the participants with the cover page face down. At this point, one of the board members declares his contempt for the proceedings, takes the report without looking at it, stands and begins walking out of the room. For a moment, he pauses, glares at me and then throws his copy into the garbage.
This is the following process:
ie it is an instance of deleting. This demonstrates that even when information has been given to a participant, he can simply delete it. The efficient market hypothesis would fail to describe this instance. Another funny gag would be that he pretended to read it, but didn’t. In that case, I believe that he has updated his belief (as I did) but he didn’t.
Isn’t “utility maximization” or “action minimization” just fluff? Mathematically we compute roots of equations and later interpret them as maxima or minima of some utility or action function. Is it good fluff? I think so. In any case from someone denying the importance of profit maximization in economics I would rather buy a car than read their book or blog.
“The only scientific truth about capitalism is its radical indeterminacy, a condition which makes it impossible to use science’s tools (e.g. calculus and statistics) to second-guess it.”
One can replace ‘capitalism’ by ‘path of an electron’ in the above quote to show that it is unjustified. Its not the electron or science, its the notion of path that is contradictory. In economcs it could well be that is makes no sense to define price and demand for a good at each time with arbitrary precision (cf. C. Schwarz from Duisburg/Essen for thoughts into that direction).
Profit maximisation is not a good career move for an executive. Meeting and ever so slightly exceeding the political demands from the stockholders for required return is a good career move. Windfall profits provide no benefit to those who actually make decisions in the modern firm, unless they are completely risk-free and come with no strings attached (which they never do, if for no other reason then because shareholders are stupid and come to expect such windfalls if you start passing them on).
(And no, stock options does not solve this problem, because they simply give the executive an incentive to maximise short-run share price – which is only weakly related to long-run profits.)
How about stock options that executives can use only after some time has passed, like after 3 years?
If you release the options only three years after he has left the firm, sure they become less toxic. And if you index them to some relevant basket of stocks, they will even prevent the executive from simply riding a bull market.
Of course this leaves aside the question of whether you would want the executive to run the firm like a stockholder would want to. The stock market is the financial institution with the highest discount rate of all financial institutions, so profit optimisation according to the stock market’s discount rate is unlikely to optimise social welfare according to society’s discount rate. For instance, a discount rate of 10% per year corresponds roughly to ignoring everything that takes place more than 70 years in the future. I am not wholly sanguine about running – say – nuclear waste disposal facilities on that principle…
The executive is just maximizing a different profit function (maybe his own salary).
You are now assuming your conclusion.
Of course, you may always impute a utility function from observed behaviour, but then you are no longer in the realm of making testable predictions about cause-and-effect relationships.
Assuming that in the principal-agent relation the principal and the agent have different utility functions is certainly not circular. A quick check on the Wiki (principal-agent problem) shows that at least there nobody considered this a reason to dismiss utilitiy maximization. Maybe I do not fully understand your reasoning.
My original remark was just meant to point out that utilitiy maximization plays a role in economics and one needs good reasons to eradicate it from the theory.
“My original remark was just meant to point out that utilitiy maximization plays a role in economics and one needs good reasons to eradicate it from the theory.”
Occam’s razor should suffice. I have yet to meet a utility function that could not be removed without loss of generality.
“The executive has a different utility function than the shareholder” is not an explanation of executive behaviour. It’s an ad hoc hypothesis constantly morphing to evade testability.
But economics and quantum mechanics are not comparable systems. In QM, the outcome of any individual experiment is unpredictable, but due to the universality of the theory, general statements can be made in terms of probability distributions. We do not yet have an economic model that can reliably predict even general trends to the same accuracy.
Classical mechanics assumes that the system being studied is independent of the observer. QM accounts for the fact that observation of small details can affect the results of an experiment, but evidence thus gathered can be used to build a theory that tells us something about what happens to systems when the scientist steps back and ceases observing the fine details. In economics, the scientist cannot step back. Knowledge of the system can be used to game the system, and every new discovery leads to new behaviour. It is not just observation that affects the experiment, but the very act of theorising itself. The only way out of this bind is for the theorist to stop publishing, for fear that his thoughts will affect the behaviour of that which he is studying.
If QM was a universal theory we could just use it to answer economic questions. It has its limits and within this limits its accurate. The same can be said about some (micro-)economic theories e.g. on wages and firm behaviour being put forward so far.
Your point on the object/subject separation is valid. Is it always relevant? Let me give you an example. I have recently learned about a new theory on firm decisions on global sourcing of complex production processes (e.g. where do I build the components of a car and with how many suppliers). I found the maths, the data and the results convincing. I doubt that company executives care about the results. The object (set of companies in a country producing a certain good) is thus suffciently separarted from the subject (several active groups of economists distributed over world).
If we consider theories working with prices and demand for goods being sharply defined for each point in time we run into the trouble you describe. In first approximation I do not consider this a problem of the scientific method. Rather, such a construction is as non-sensical as the notion of path in QM.
Uwe wrote:
This is a very interesting issue.
As you know, anything that happens can be regarded as minimizing or maximizing some quantity—in fact, infinitely many different quantities. (For example, it minimizes the distance between what could happen and what actually does, and there are many ways of defining this distance.)
So, the claim that people maximize some quantity is, taken by itself, completely without predictive power. We need to add some extra assumptions to get a framework that says something nontrivial.
So, when economists model people’s behavior in terms of
maximizing ‘utility’, what really matters is the simplifying assumptions built into how utility is computed.
In his book Rationality and Freedom, Amartya Sen questions some assumptions like these:
• Self-centered welfare: A person’s welfare depends only on their own consumption and other features of the richness of their life (without any sympathy or antipathy towards others, and without any procedural concern).
• Self-welfare goal: A person’s only goal is to maximize their own welfare.
• Self-good choice: A person’s choices must be based entirely on the pursuit of their own goals.
One could list many more.
In classical physics, the action principle is not just fluff because we say a physical system minimizes some ‘action’ that’s an integral over time of some function of its position and velocity. This gives rise to a whole slew of powerful concepts like energy, momentum, conserved quantities coming from symmetries, etcetera.
It also has the advantage of being well confirmed by experiment!
What about economics?
I won’t try to answer that. Instead, I’ll just add that in quantum physics, a system no longer minimizes the action: it takes all possible paths, weighted by the exponential of times the action. So, things get trickier here, and the analogy to economics seems even weaker to me.
times the action. So, things get trickier here, and the analogy to economics seems even weaker to me.
I don’t think Varoufakis’ “inconsistency” is meant in the logical sense. His “inherent flaw” is the attempt to achieve ‘closure’ in economic theories which necessarily prevents the model from describing economic innovation and change. The claim is that evolving complex systems cannot be described by finite-dimensional, closed systems of differential equations, and attempting to do so misses something essential about them. The same issue arises in physics, ecology and economics.
Take physics first. In fluid dynamics, people have tried to capture the fine structure of turbulent flow by looking at the moments of energy, momentum, or vorticity fields. When they do this, they find that the successive moments satisfy PDEs with a driving or noise term which can be expressed in terms of a higher order moments. This results in an infinite hierarchy of PDEs. When people attempt to make this finite by imposing some closure condition in which come high order moment is a local function of lower order moments, closure is achieved but the resulting system of equations fails to reproduce the observed fine structure of turbulent flow. Sorry for the sketchy explanation – I’m just remembering stuff from a workshop 13 years ago…
Then there’s the period-doubling cascade on the way to turbulence. At any given point in the laminar regime a flow would be described by infinitely many modes, most of which will decay exponentially. The finitely man ones that don’t define an effective finite dimensional system of ODEs which describes the flow. This finite-dimensional system is a stable attractor, as all the other modes decay. But, as the reynolds number is increased, one of the decaying modes becomes marginal and then unstable. At that point, any noise will be amplified exponentially in the direction of this new mode, which will eventually saturate when nonlinear effects kick in. The result is an increase in the dimension of the effective system of ODEs describing the fluid flow. But dimension change is not something that can be described within an ODE framework, only when the ODE is explicitly seen as a finite dimensional approximation to a PDE.
In ecology, dimension change is akin to speciation. Population dynamics of an ecosystem can be modelled by a finite-dimensional ODE. But this is unable to describe speciation, which increases the dimensionality of the system in an unpredictable direction (one cannot pre-specify the behaviour of the new dimension, that is, one cannot write an n+1 dimensional system and pretend that the system initially lives in n dimensions until some random perturbation starts growth in the n+1st dimension). So, “an engineering approach to ecology” won’t be able to capture evolution or speciation even if it accommodates changing environmental conditions.
Stuart Kauffman modelled biological systems as “autocatalytic networks”, and in his book “At Home in the Universe” he proposes an economic application of autocatalytic networks. He describes the economy as a system in which combinations of some products yield other products. This is similar to “pure production models” such as those of Piero Sraffa or Wassily Leontieff, which give rise to finite-dimensional systems of equations. What these models cannot capture is economic innovation: the appearance of entirely new products and markets which change the dimensionality of the system.
Curiously, there’s a paper by Kauffmann and Lee Smolin about “The Problem of Time in Quantum Gravity” where they relate these issues to cosmology. They say “There is an analogous issue in theoretical biology. The problem is that it does not appear that a pre-specifiable set of “functionalities” exists in biology, where pre-specifiable means a compact description of an effective procedure to characterize ahead of time, each member of the set. This problem seems to limit the possibilities of a formal framework for biology in which there is a pre-specified space of states which describe the functionalities of elements of a biological system. Similarly, one may question whether it is in principle possible in economic theory to give in advance an a priori list of all the possible kinds of jobs, or goods or services.” Again, the problem is that, by imposing closure on the theoretical description, an essential feature of the system is left out.
I don’t know if anyone has mentioned this but the reality may be described by game theory. If a universal model of the behavior of a financial market existed, and everyone had access to it, then no one could make any money off of it. Everyone would predict the same market direction and there would be no losses to make up for the gains. There is a name for this law, and I think it may be related to Goodhart’s Law or the Lucas critique.
It’s one of those rules that once you understand it, you realize what a game the whole speculative financial system is.
Right. I don’t know what this rule is called.
One interesting side-remark is that you can—at last in theory!—have insights that let you profit in financial markets as long as you keep them secret and don’t push them so hard that they break down. It’s possible that Jim Simons is doing this, or trying to. He’s a famous mathematician who now runs a $15 billion hedge fund.
But there’s something else that’s much more interesting to me.
There’s a certain kind of insight about the economic system that you can publicize without making it cease to be true. Roughly speaking, this is the kind of insight that helps us cooperate to make lots of people happier. Economics is not a zero-sum game, after all. Some insights let everyone—or at least most people—become happier. And some of these insights work better when more people have them.
These are the insights I care about. In fact, the previous paragraph may be one of these insights.
The Azimuth Library has a nice article on Goodhart’s law, written by David Tweed. It’s a bit different than what we’re talking about now:
This is frequently asserted, but not actually true, because capital markets do fulfill more functions than an elaborate casino. If they did not, we could simply padlock the City of London and ship all the gamblers off to Casino Royale.
What it would do is force the money markets to focus on their legitimate functions, namely capitalising and fixing prices for productive companies.
I have thought about this for a bit, so I will try to add an actual technical comment.
A market is a place where people negotiate the price of an item by making bids or sales or entering future contracts at given prices (and complex derivatives are of the same nature). By stating that I want to sell X, I am telling the rest of the market goers that I believe that X is too highly valued. My internal belief about the market as a whole, the values of all the items and the state of the world are hidden. The only thing that people see are my bids or sales.
We say there are two networks. First, there is the network of items and processes. This is the foundation of the entire system. The items are things like corn, and processes are everything from “eating the corn” to “grinding the corn then adding water and enzymes to convert” the corn to dextrose.
Next is the network of buyers, sellers and consumers. It would be good to see this as the same network. The consumers can definitely be seen as parts of the first network. The buyers and sellers, for now, will be considered separate. In this network, B, a buyer is a wire. This wire represents the hidden buyers beliefs as mentioned above. Regular, or classical information (like bids and newswires) lives in this network too. However, we make a distinction between the hidden beliefs that a buyer holds and the classical data of sales and bids. This distinction is represented in the graph by putting the “data” wires inside dotted lines. The beliefs cannot be copied, but the data can. So a data wire can turn into two data wires representing the copying of the data. The category is a symmetric monoidal category and the diagrams are the string diagrams. A box is a transformation of a belief, or the copying or deleting of information. A data wire can be placed next to a belief wire and tensored together (tenatively) by forgetting the copy/delete morphisms. The resulting tensored wires are in the base symmetric monoidal category. They can pass into a box. Out the other end comes the updated belief wire.
So, we have two networks. One is the raw material processing and concurrent scheduling of what gets processed before what. The second, B, is the belief network. These two form the market. A typical belief might be that, in the next phase of the process network (the network can evolve), a new box will be added for the further processing of some material. That is, someone thinks that a new invention will occur, like the processing of corn dextrose into ethanol alcohol. This belief leads to the conclusion that the corn dextrose will have higher value in the future, as it can be used to make fuel for cars. The holder of this belief then makes a high bid for a corn contract in the future.
To model this bid, we produce a blank-data wire, out of nothing, combine it with a belief wire by passing it into a box, and out comes a data wire. The outcoming data wire represents the bid. It can be copied and combined with other buyer’s belief wires to update their beliefs.
Here is a link to the diagram of the aforementioned process of sharing information.
To sum up, we have a symmetric monoidal category of beliefs, and in this category we also have an internal category of comonoids. The comonoid objects are seen as “data wires” in the string diagrams.
That is an … interesting description of a market.
Interesting mostly because it writes out very nearly every socially useful function that markets perform.
Jakob: it would help Ben more if you told him some of the things his concept of the market omits.
Markets are an institution that permit specialisation by allowing people who overproduce a good relative to their needs to exchange it for goods they underproduce relative to their needs in an orderly fashion and under a stable institutional framework.
Slightly more sophisticated markets allow people to exchange goods and services without those goods and services being physically present at the market site (so you can make your sale before expending resources on transporting the goods to market).
Even more sophisticated markets allow people to exchange expected future production for expected future needs in a stable institutional framework. The institutional stability becomes particularly important in the latter two cases, because the transactions are to take place in the future rather than immediately.
Prices is the least interesting function of markets, not the least because markets do not set most prices that are actually important to the material provisioning of society.
Bob Coecke and Rob Spekkens have mapped out, in great detail, the ideas of belief propagation and update.
They are using Frobenius algebras and those are what I was thinking of when speaking of the comonoid.
Jacob,
Yes, I agree that the market does other things. However, I stand by my post and here are some extra comments.
I am guessing that you are looking at the market as if information about any one thing is always instantaneously propagated to every other market participant. This is the efficient market hypothesis. If you talk to a good, experienced value investor, he will likely point out that the efficient market hypothesis is not a good axiom to apply to a market. As you can see from my diagrams, and this is inherent in what all my colleagues do, data must flow from participant to participant and does so in the structured manner which I have pointed out. In fact, time itself is nothing but the ordering relations in the graph. There is no universal clock.
So in this case:
Markets are an institution that permit specialisation by allowing people who overproduce a good relative to their needs to exchange it for goods they underproduce relative to their needs in an orderly fashion and under a stable institutional framework.
The presence of a market player with an abundance must be transmitted as a message to the other participants and this can be seen as an offer to sell at some low price. Not until that message is sent does it become part of another player’s belief about the world as a whole. As the information propagates, people’s beliefs can be updated. Lower volatility in a price means there is a good consensus as to what’s going on in the world and what is likely to happen in the future.
I still maintain that the market is there for us to come to consensus as to what is going to happen in the future. What markets do is attempt to provide stability in an unstable world and that stability is nothing but consensus of belief as to what is about to come.
Slightly more sophisticated markets allow people to exchange goods and services without those goods and services being physically present at the market site (so you can make your sale before expending resources on transporting the goods to market).
The data that there is an abundance somewhere in the world (right “now”) is brought to the market by the seller. His coming to market is part of the transmission of information. Think of it this way. If I don’t know you have an abundance at the moment I want to buy, then in my mind, you don’t. We can discard the notion that there is an absolute state of the universe at a time point (Efficient market hypothesis). Replacing it, instead, with an evolving consensus as to what the universe consists of.
Even more sophisticated markets allow people to exchange expected future production for expected future needs in a stable institutional framework. The institutional stability becomes particularly important in the latter two cases, because the transactions are to take place in the future rather than immediately.
Again, if a market player knows they will have a need in the future, this is data that needs to propagate through the market (network). I have shown how this works.
The value of my posting is that there is now (or soon will be) a calculational alternative to any model based on the efficient market hypothesis. It specifically takes into account information flow and we see this then goes straight towards having a mathematical model of belief update. That is a very valuable bit of new knowledge.
I tried to mark what was a quote but failed. oops.
Heavens, no. I’m looking at the market as being composed of equal parts banksters, economic hit men and clueless marks. Information seems to play a very small role compared to raw power and base stupidity.
Which of course is the reason that “the markets” are not allowed to regulate the prices or volumes of anything genuinely important in a properly run industrial society.
Naturally. However, only a severely secluded market participant could fail to notice that CocaCola has fizzy drinks for sale, or that US Steel would like to relieve its stockpiles of excess ferrous alloys. It does not seem particularly credible to assert that price movements in these goods convey information, rather than – say – reflect changes in power relationships between different market actors.
That is one way the information can be transmitted, but far from the only one, and for most industrially interesting commodities not the most important one either.
If what you want to model is what the gamblers are doing, sure, the casino floor – sorry, marketplace – is the most important social environment. But I submit that this gambling is not the primary social benefit of having organised markets. In fact, a rather large number of regulations have in the past been passed for the explicit purpose of moving this activity to Las Vegas where it more properly belongs.
Markets are spectacularly bad at that. Which is why no industrial planner in his right mind would build a nuclear reactor, a railway, a wind farm or a pipeline without having secured long-term fixed-price agreements to cover his capital costs. Liquid markets simply do not exist for most industrial infrastructure, capital plant and intermediate goods (and even for consumer goods the market is heavily managed through propaganda, market power and more heavy-handed forms of price fixing), because liquid markets for capital-intensive goods are, well, Epic Fail.
Sure, you can use futures markets to hedge those risks, but that strikes me as a jobs programme for the City of London more than a way to mitigate actual uncertainty.
That is undoubtedly interesting new knowledge. And even if it were not interesting for its own sake, I can think of a number of applications. Studying market behaviour is, however, not one that comes immediately to mind.
– Jake
What do you guys think of the idea of “implied correlation”? That is where the gains of the stock market move in sink, and there is barely any differentiation in individual stock price movements. It has been as high as 80% recently.
I would think if it ever hit 100%, it would be completely casino, and nothing to do with investment outlook except for the economy as a whole.
It depends on the circumstances. Sometimes it’s just noise – something spooked the crack ferrets (a major corporation over- or undershot expectations in its quarterly report). Sometimes it’s a legitimate reaction to a policy change – if the central bank raises the policy rate, you would expect all stocks to drop as stockholders liquidate to take advantage of this increase in the lazy money subsidy.
But generally it’s not worthwhile to attempt to model daily noise, unless you’re in the noise trading business. In which case I personally believe that your place of employment should be moved to Las Vegas, where you can make more socially beneficial use of your skills.
John Baez wrote:
One point of contact is the issue of dynamics in a multipartite system. What if, instead of just tracking the overall number of rabbits, we label organisms by their site, and we introduce processes which relate one site to another — migration, dispersal and so forth. (Yes, it’s my role to harp on spatial dependence, but I think it’s pertinent here, and right now I’m just thinking about a general notion of a “structured population”.) The connections from one site to another, the allowed transitions made possible by migration and dispersal processes, have the topology of a graph, or a network if you’re not so much a mathematician by training.
Instead of having just one pair of creation/annihilation operators, and
and  , we define a whole set, indexed by the site label
, we define a whole set, indexed by the site label  , with
, with
and in the “stochastic Hamiltonian” which gives the time-evolution of our states, we incorporate the adjacency matrix of the graph, so that what happens at
of the graph, so that what happens at  doesn’t have to stay at
doesn’t have to stay at  if
if  .
.
The work I’ve seen in this direction then takes the continuum limit in which the lattice of sites becomes a continuous field and the adjacency matrix becomes a kernel of some sort. It would be interesting if one could develop these notions for a more “complex” graph topology of the sort studied in (what other people call) network theory. There’s a whole world of possibilities in between dynamics-on-a-lattice and dynamics-on-a-complete-graph!
Another possibility, which I haven’t thought so much about yet, is to treat the possible edges in a graph as dynamical variables. Creating an edge between vertices and
and  is the job of the operator
is the job of the operator  . If we want edges to be binary things, either existing or not, then we could switch over to “fermionic” operators. The stochastic Hamiltonian would then couple edges which have vertices in common. We could then have a model of the probabilistic evolution of a network over time, with new edges forming and old edges breaking down.
. If we want edges to be binary things, either existing or not, then we could switch over to “fermionic” operators. The stochastic Hamiltonian would then couple edges which have vertices in common. We could then have a model of the probabilistic evolution of a network over time, with new edges forming and old edges breaking down.
I think the idea of treating edges as dynamical variables is really cool!—and potentially very important in ‘network science’.
But not just edges, right? Vertices, too, can come and go.
One wants, for example, some model of how the world-wide web grows. Or for that matter, a brain. Connections between neurons tend to form when there’s correlation between the activity of these neurons. Furthermore, ‘unused’ neurons tend to die, and new ones can apparently grow ‘as needed’.
(I don’t know how the brain tells when some neurons are ‘needed’. Presumably there’s some characteristic feature of a region of the brain being ‘overused’.)
You got me curious about neuron death, and here’s something about that:
• James B. Hutchins and Steven W. Barger, Why neurons die: Cell death in the nervous system, The Anatomical Record 253 (6 December 1998).
A quote:
Yes!
In network science, one can study the dynamics of a network — nodes being added or removed, edges being rewired — or the dynamics on the network — spins flipping from up to down in an Ising model, traffic flow along subway routes, an infection spreading through a susceptible population, etc. These have often been studied separately, on the rationale that they occur at different timescales. For example, the traffic load on the different lines of the Boston subway network changes on an hourly basis, but the plans to extend the Green Line into Medford have been deliberated since World War II.
In the past few years, increasing attention has been focused on adaptive networks, in which the dynamics of and the dynamics on can occur at comparable timescales and feed back on one another. A few references:
K. Fehl et al. (2011). “Co-evolution of behaviour and social network structure promotes human cooperation” Ecology Letters 14: 546–51. PubMed:21463459.
T. Gross and B. Blasius (2008). “Adaptive coevolutionary networks: A review”. J R Soc Interface 5, 20: 259–71. PubMed:2405905.
T. Gross and H. Sayama, eds (2009). Adaptive Networks: Theory, Models and Applications. Springer.
C. Kamp (2010). “Untangling the interplay between epidemic spread and transmission network dynamics” PLoS Computational Biology 6, 11: e1000984. PubMed:2987842.
M. Perc and A. Szolnoki (2009). “Coevolutionary games — a mini review”. BioSystems 99: 109–25. arXiv:0910.0826.
L. B. Shaw and I. B. Schwartz (2010). “Enhanced vaccine control of epidemics in adaptive networks” Physical Review E 81, 4: 046120. PubMed:2931598.
S. Van Segbroeck, F. C. Santos, and J. M. Pacheco (2010). “Adaptive contact networks change effective disease infectiousness and dynamics” PLoS Computational Biology 6, 8: e1000895. PubMed:2924249.
B. Wu et al. (2010). “Evolution of cooperation on stochastic dynamical networks” PLoS ONE 5, 6: e11187. PubMed:2894855.
(Disclaimer: I’ve met Thilo Gross and worked with Hiroki Sayama, but I don’t have any financial stake in the success of the anthology they co-edited.)
Wow, what a lot of references! Thanks!
Hey,
If we model our network as a diagram in a category, and the evolution of the network as a functor or endofunctor, can we still lose edges? I don’t think you can…blurg. What about a string diagram in, say, FdHilb. In that case, we lose edges according to the rewrite rules of the diagram and those rules are the axioms of the category itself. In that sense, we lose or gain edges according to the axioms of the category. I took as an example the simplest diagram: the commutative triangle. You can’t map the commutative triangle to an exact copy of the diagram with one edge missing. Functors won’t allow that. You can collapse it to a parallel pair of arrows, where one arrow went to the identity. Just breaking off an edge seems to be not allowed.
Category theory is such a broad and general thing that I don’t know where one should start trying to mix it with the network-science business. For example, the fact that we have these creation and annihilation operators suggests that there’s something like groupoidification lurking about. Maybe time-evolution from one probability distribution over the possible numbers of rabbits to another such distribution can be thought of using spans of groupoids?
(Which reminds me: I had a half-formulated idea about stuff types and statistical physics from last year — kind of pursuant to this conversation last summer — which I really out to dig out again and do a sanity re-evaluation upon.)
I remember discussing an experiment with a guy who worked in the field of decision theory.
There was a bag made of black velvet and the experimenter put several (if I can remember correctly 8) blue marbles in it one by one and a yellow one in addition in front of the subject. Then the subject was told the experimenter would pull marbles out of the bag, one at a time, in a random fashion and the subject was supposed to bet on it being yellow.
Of course the more blue marbles were out the more likely it got the next one would be yellow, so as the experiment proceeded, rational bets should have changed accordingly. One can even calculate (quite easily) what the best strategy is.
However, in fact people followed a different course, which was labelled “irrational” by the guy I was talking with. Unfortunately I can’t remember the details of observed behavior, but it is not important anyway.
Because there was a secret detail, which was not communicated to the subject. There was a pocket inside the bag and the experimenter developed a certain skill to insert the yellow marble in it, unnoticeable to the subject, while all the blue ones just went into the rest of the bag. This way he was able to pull out the yellow marble invariably as the last one, so it was easy to compare betting strategies recorded over many subjects.
Now, the model over which “rational” strategy was calculated has not included this arcane detail, because subjects were not supposed to know about it.
What I did was to recalculate “rational” strategy with assigning an unknown probability to the event the experimenter was cheating in this particular way. It made sense to suppose this probability was non-zero, because this was what actually happened. And it turned out there was a certain probability at which observed behavior got pretty close to the theoretical optimum.
Now, what can we make of it? I honestly believe subjects have not known about the cheat, so how could they take it into account when developing their strategy?
I believe they did something more general and the match with a certain value of probability assigned to this kind of cheat was happenstance. It served as just another degree of freedom, which in this case was enough to bring theory close to reality.
So. What did subjects do?
Well, it is general human experience that our perceptions of reality are not perfect. Therefore, when acting, we should also take into account the fact that the perception our intended action is based on may be flawed. And it can be flawed in many unconceivable ways, so one never knows for sure. Still, we have to do *something*, so we can’t escape taking into account the uncertainty in advance.
I do not know how to model this kind of situation, but we all manage somehow, even if the bulk of the thought process is hidden and deeply unconscious.
When human interaction is involved (as in the experiment described above), mis-perception is almost inevitable, because people always try to outsmart each other and most of this outsmarting effort goes into evoking certain perceptions of the situation in others. Even honest people do it all the time, because this is what communication is about. The only difference is that they *believe* their interpretation of reality is adequate and they communicate it as such, but there is no guarantee it is actually the case. One can (and often do) cheat on oneself after all.
Not to mention the fact that people are not always honest (as it was the case with our experimenter).
This anything goes approach is quite prevalent in economics, it is enough to think about clients of Mr. Madoff.
However, the first law of decision theory is more general than that.
1. Rare events happen often.
It means there are many events in our lives which are extremely rare in the sense they only happen at most once in a lifetime, but some of which are quite influential on our personal fate. All of us can tell many such stories. And it is absolutely infeasible to enumerate such events in advance, so we can not prepare for them beyond the general attitude “one never knows”.
Individual events which are rare in themselves collectively make up a considerable portion of all the events experienced.
This fact can get rather serious when people try to develop sophisticated probabilistic models for risk management in fields like nuclear plant operations or airplane design.
When scenarios of actual industrial catastrophes are analysed in retrospect, almost inevitably one finds such elements in the chain of events leading to disaster which no one ever considered in advance. Not because they were deemed to be impossible, but because they had not even occurred to anyone.
There is no way to define a probability measure if the sample space is not given.
Berényi wrote:
This is related to Migeruet’s observation above:
Yes, looks like the same kind of closure problem. I wonder if it is related to Chaitin’s work on algorithmic information theory.
Also, I have noticed similar behavior while working on linguistic analysis problems (for automatic speech recognition). I was trying to “count” word-forms in Hungarian (which is an agglutinative language and as such, is quite productive on the morphologic level). It turned out the language may have an infinite number of valid word-forms (in the same sense all natural languages have a [potentially] infinite set of sentences). What is more, there is no straightforward way to enumerate them all, so a complete dictionary is beyond reach. Therefore no amount of statistics is sufficient to define a probability distribution over the set of (Hungarian) word-forms (valid strings of alphabetic characters between spaces).
Of course, Hungarian spell checker is not based on simple dictionary lookup, but has a morphologic analyzer in its tummy. Even so, it can miss quite a lot of weird words (which are understandable to native speakers nevertheless).
KleinberG.
Were these the monkeys-with-coins experiments that straightaway led to prostitution?
Okay, fixed:
• David Easley and Jon Kleinberg, Networks, Crowds and Markets: Reasoning about a Highly Connected World, Cambridge University Press, Cambridge, 2010.
In my endeavor to figure out if you were just yanking my chain, I unearthed:
• Krist Mahr, Do monkeys pay for sex?, Time, 7 January 2008.
but that’s about long-tailed macaques, not capuchins—and no coins. Then I dug deeper and found:
• Stephen J. Dubner and Steven D. Levitt, Monkey business, New York Times, 5 June 2005.
which talks about Keith Chen, an economist who works with Laurie Santos on capuchin monkeys:
This may be the first blog post to spawn highly relevant comments both about annihilation and creation operators and about monkey brothels. But note: Allen Knutson is to blame for the latter.
I remember there was an article in Scientific American about bonobo monkeys (/apes/whatever). They appear to have behaviours in the wild where a male will give a female fruit before they engage in sex. As a follow-up letter noted, quite how you interpret what that denotes can depend what your view on whether the female enjoys sexual intercourse in itself (noting that no-one seems to believe other than that the male bonobo’s view on it).
IIRC the overall view of the article was that bonobos have complicated “social” behaviours, but it’s easy to assign human motivations which may not apply.
You can lead a horse to water but you can’t make him drink. The failing of the efficient market hypothesis in a hilarious diagram.
Yeah, I’ve been weary of economics since it’s as rigorous as fortune telling…however, that’s only the marginalist-based stuff (Sraffa actually wrote a brilliant critique of it back in the 1960s).
There are very few thinkers who produce good work, some of it can be quite interesting — e.g., Eric Beinhocker’s The Origin of Wealth is an interesting semi-layman’s description of complexity economics.
But it’ll be a cold day on Venus when economics is rigorous, or even internally consistent.
I’ll focus on a similar question that Tim van Beek posed on this blog: You have two kinds of fertilizer, A and B. You know that of 4 trees who got A, three thrived and one died…
Dear John Baez,
I just found out about the Azimuth work and will try to follow.
Recall that someone once said “If you want to do important work, work on important problems.”
On the use of math in economics here’s an article about “neuroeconomics” that might be interesting–
http://www.project-syndicate.org/commentary/shiller80/English
A possible way to apply neuroeconomics to Azimuth goals might go like this–
A. Study mathematical models of optimal capital budgeting and apply through think tanks like the Brookings Institution to suggested policy making.
For example, a model of optimal capital budgeting can be based on “probability learning.”
B. Based on the mathematical model, in the lab study what makes for the best performance in learning probability (and so optimal capital budgeting, now to include environmental factors per Azimuth perspectives).
For example, from experiments it’s know that teams of two perform better at difficult problems than other sized teams. The team of two can often outperform the highest performing individual in difficult problems.
So in the lab, using for example (a) instruments to study neuroeconomic phenomena and (b) experimental game theory, find what skills should be devleoped to optimize probability learning by teams of two and how collections of teams of two can perform optimal capital budgeting (now defining optimality according to Azimuth perspectives).
c. Transfer results from the lab into training courses on negotiation and decision making in business schools. As well, develop computer- and media-based “assessment centers” and transfer to small start ups focused on helping companies develop and select candidates for key positions. At the same time develop software that can be used by companies to support optimal capital budgeting. Specify the software so it can supply non-proprietary information to analysts, credit ratings agencies and perhaps even government regulators.
Here is a little more detail–
Neuroeconomics came from behavioral economics, in which probability learning was a puzzle because it did not appear to be optimal for an individual and so violated the “utility maximizer” model in mathematical economics.
But probability learning is widely evident in creatures from fish to humans. And it seems to have been selected by evolution as optimal; yet in the mathematical economics of the utility maximizer, it is not optimal.
The neuroeconomics literature will point you to the likes of C. Randy Gallistel and his book “The Organization of Learning.”
Although it doesn’t seem to be explicit anywhere that I’ve looked, probability learning is key to the process of optimal foraging.
On probability learning–
Gallistel pitted sophomores in his class agains a lab rat. The rat had two rat-sized hallways with food delivery at each end. A light above would signal to the sophomores which of the two channels where food appeared in a trial.
The appearance of the food followed a probability distribution– 25 percent of the trials it appeared at channel A. 75 percent of the time it appeared at channel B.
On each trail students are asked to guess on paper which channel, A or B, will give the food.
And the rat is given the choice to enter either channel A or channel B.
What the class finds at the completion of the trials is that students learn the probability involved.
Their guesses are 25 percent of the time channel A and 75 percent of the time channel B.
The amount of food they would get is calculated.
Then Gallistel compares to the amount of food the rat got from running the trials.
Fairly quickly it has settled on channel B where 75 percent of the food occurs.
So the rat outperforms every student in the class at getting food.
The rat performed like a “utility maximizer” but the students did not.
Why?
Gallistel’s set-up gives different information to the students compared to the rat.
The students see the light turn on when food occurs at either channel, but the rat does not. It is not allowed to see the light.
When it is given the same information, it also performs probability learning.
On optimal foraging–
In the same book, Gallistel describes optimal foraging by schools of fish.
By a probability distribution, prey fish come out of two different tubes in the water separated by some distance.
25 percent of the time, the prey fish come out of channel A. 75 percent of the time, they come out of channel B.
Very quickly, the predator school of fish divides itself into two sub-schools. 25 percent of the original school feed at channel A.
75 percent feed at channel B. After the school divides itself into these two sub-schools, it is rare to see any individual fish travel from one feeding tube to the other.
What’s needed is a mathematical model of probability learning (I use Shannon-like terms),
Then in the school foraging situation, model how (just as for the rat in the classroom) Shannon-like information terms for the unvisited channel are attenuated.
These mathematical models can be applied to the capital budgeting process in firms. Each dollar bill is like each fish in the school.
When equilibrium is reached in optimal foraging as above, the food per fish is the same for each channel. No individual fish can improve its situation by travelling to the other channel.
It’s a Nash equilibrium with no fish wasting effort to travel to the other channel.
So probability learning produces optimality at the level of the school of fish.
But for an individual (fish) alone, probability learning is not optimal, just as for the college sophomores in Gallistel’s experiments.