guest post by Matteo Smerlak
Introduction
Thermodynamical dissipation and adaptive evolution are two faces of the same Markovian coin!
Consider this. The Second Law of Thermodynamics states that the entropy of an isolated thermodynamic system can never decrease; Landauer’s principle maintains that the erasure of information inevitably causes dissipation; Fisher’s fundamental theorem of natural selection asserts that any fitness difference within a population leads to adaptation in an evolution process governed by natural selection. Diverse as they are, these statements have two common characteristics:
1. they express the irreversibility of certain natural phenomena, and
2. the dynamical processes underlying these phenomena involve an element of randomness.
Doesn’t this suggest to you the following question: Could it be that thermal phenomena, forgetful information processing and adaptive evolution are governed by the same stochastic mechanism?
The answer is—yes! The key to this rather profound connection resides in a universal property of Markov processes discovered recently in the context of non-equilibrium statistical mechanics, and known as the ‘fluctuation theorem’. Typically stated in terms of ‘dissipated work’ or ‘entropy production’, this result can be seen as an extension of the Second Law of Thermodynamics to small systems, where thermal fluctuations cannot be neglected. But it is actually much more than this: it is the mathematical underpinning of irreversibility itself, be it thermodynamical, evolutionary, or else. To make this point clear, let me start by giving a general formulation of the fluctuation theorem that makes no reference to physics concepts such as ‘heat’ or ‘work’.
The mathematical fact
Consider a system randomly jumping between states with (possibly time-dependent) transition rates
where
is the state prior to the jump, while
is the state after the jump. I’ll assume that this dynamics defines a (continuous-time) Markov process, namely that the numbers
are the matrix entries of an infinitesimal stochastic matrix, which means that its off-diagonal entries are non-negative and that its columns sum up to zero.
Now, each possible history of this process can be characterized by the sequence of occupied states
and by the times
at which the transitions
occur
:
Define the skewness of each of these transitions to be the logarithmic ratio of transition rates:
Also define the self-information of the system in state at time
by:
where is the probability that the system is in state
at time
, given some prescribed initial distribution
. This quantity is also sometimes called the surprisal, as it measures the ‘surprise’ of finding out that the system is in state
at time
.
Then the following identity—the detailed fluctuation theorem—holds:
where
is the cumulative skewness along a trajectory of the system, and
is the variation of self-information between the end points of this trajectory.
This identity has an immediate consequence: if denotes the average over all realizations of the process, then we have the integral fluctuation theorem:
which, by the convexity of the exponential and Jensen’s inequality, implies:
In short: the mean variation of self-information, aka the variation of Shannon entropy
is bounded from below by the mean cumulative skewness of the underlying stochastic trajectory.
This is the fundamental mathematical fact underlying irreversibility. To unravel its physical and biological consequences, it suffices to consider the origin and interpretation of the ‘skewness’ term in different contexts. (By the way, people usually call the ‘entropy production’ or ‘dissipation function’—but how tautological is that?)
The physical and biological consequences
Consider first the standard stochastic-thermodynamic scenario where a physical system is kept in contact with a thermal reservoir at inverse temperature and undergoes thermally induced transitions between states
. By virtue of the detailed balance condition:
the skewness of each such transition is
times the energy difference between the states
and
, namely the heat received from the reservoir during the transition. Hence, the mean cumulative skewness
is nothing but
with
the total heat received by the system along the process. It follows from the detailed fluctuation theorem that
and therefore
which is of course Clausius’ inequality. In a computational context where the control parameter is the entropy variation itself (such as in a bit-erasure protocol, where ), this inequality in turn expresses Landauer’s principle: it impossible to decrease the self-information of the system’s state without dissipating a minimal amount of heat into the environment (in this case
, the ‘Landauer bound’). More general situations (several types of reservoirs, Maxwell-demon-like feedback controls) can be treated along the same lines, and the various forms of the Second Law derived from the detailed fluctuation theorem.
Now, many would agree that evolutionary dynamics is a wholly different business from thermodynamics; in particular, notions such as ‘heat’ or ‘temperature’ are clearly irrelevant to Darwinian evolution. However, the stochastic framework of Markov processes is relevant to describe the genetic evolution of a population, and this fact alone has important consequences. As a simple example, consider the time evolution of mutant fixations in a population, with
ranging over the possible genotypes. In a ‘symmetric mutation scheme’, which I understand is biological parlance for ‘reversible Markov process’, meaning one that obeys detailed balance, the ratio between the
and
transition rates is completely determined by the fitnesses
and
of
and
, according to
where is a model-dependent function of the effective population size [Sella2005]. Along a given history of mutant fixations, the cumulated skewness
is therefore given by minus the fitness flux:
The integral fluctuation theorem then becomes the fitness flux theorem:
discussed recently by Mustonen and Lässig [Mustonen2010] and implying Fisher’s fundamental theorem of natural selection as a special case. (Incidentally, the ‘fitness flux theorem’ derived in this reference is more general than this; for instance, it does not rely on the ‘symmetric mutation scheme’ assumption above.) The ensuing inequality
shows that a positive fitness flux is “an almost universal evolutionary principle of biological systems” [Mustonen2010], with negative contributions limited to time intervals with a systematic loss of adaptation (). This statement may well be the closest thing to a version of the Second Law of Thermodynamics applying to evolutionary dynamics.
It is really quite remarkable that thermodynamical dissipation and Darwinian evolution can be reduced to the same stochastic mechanism, and that notions such as ‘fitness flux’ and ‘heat’ can arise as two faces of the same mathematical coin, namely the ‘skewness’ of Markovian transitions. After all, the phenomenon of life is in itself a direct challenge to thermodynamics, isn’t it? When thermal phenomena tend to increase the world’s disorder, life strives to bring about and maintain exquisitely fine spatial and chemical structures—which is why Schrödinger famously proposed to define life as negative entropy. Could there be a more striking confirmation of his intuition—and a reconciliation of evolution and thermodynamics in the same go—than the fundamental inequality of adaptive evolution ?
Surely the detailed fluctuation theorem for Markov processes has other applications, pertaining neither to thermodynamics nor adaptive evolution. Can you think of any?
Proof of the fluctuation theorem
I am a physicist, but knowing that many readers of John’s blog are mathematicians, I’ll do my best to frame—and prove—the FT as an actual theorem.
Let be a probability space and
a measurable involution of
. Denote
the pushforward probability measure through this involution, and
the logarithm of the corresponding Radon-Nikodym derivative (we assume and
are mutually absolutely continuous). Then the following lemmas are true, with
:
Lemma 1. The detailed fluctuation relation:
Lemma 2. The integral fluctuation relation:
Lemma 3. The positivity of the Kullback-Leibler divergence:
These are basic facts which anyone can show: by Jensen’s inequality,
trivially, and
follows from
and the change of variables theorem, as follows,
But here is the beauty: if
• is actually a Markov process defined over some time interval
and valued in some (say discrete) state space
, with the instantaneous probability
of each state
satisfying the master equation (aka Kolmogorov equation)
and
• the dagger involution is time-reversal, that is
then for a given path
the logarithmic ratio decomposes into ‘variation of self-information’ and ‘cumulative skewness’ along
:
This is easy to see if one writes the probability of a path explicitly as
where
is the probability that the process remains in the state between the times
and
. It follows from the above lemma that
Theorem. Let be a Markov process and let
be defined as above. Then we have
1. The detailed fluctuation theorem:
2. The integral fluctuation theorem:
3. The ‘Second Law’ inequality:
The same theorem can be formulated for other kinds of Markov processes as well, including diffusion processes (in which case it follows from the Girsanov theorem).
References
Landauer’s principle was introduced here:
• [Landauer1961] R. Landauer, Irreversibility and heat generation in the computing process}, IBM Journal of Research and Development 5, (1961) 183–191.
and is now being verified experimentally by various groups worldwide.
The ‘fundamental theorem of natural selection’ was derived by Fisher in his book:
• [Fisher1930] R. Fisher, The Genetical Theory of Natural Selection, Clarendon Press, Oxford, 1930.
His derivation has long been considered obscure, even perhaps wrong, but apparently the theorem is now well accepted. I believe the first Markovian models of genetic evolution appeared here:
• [Fisher1922] R. A. Fisher, On the dominance ratio, Proc. Roy. Soc. Edinb. 42 (1922), 321–341.
• [Wright1931] S. Wright, Evolution in Mendelian populations, Genetics 16 (1931), 97–159.
Fluctuation theorems are reviewed here:
• [Sevick2008] E. Sevick, R. Prabhakar, S. R. Williams, and D. J. Searles, Fluctuation theorems, Ann. Rev. Phys. Chem. 59 (2008), 603–633.
Two of the key ideas for the ‘detailed fluctuation theorem’ discussed here are due to Crooks:
• [Crooks1999] Gavin Crooks, The entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences, Phys. Rev. E 60 (1999), 2721–2726.
who identified as heat, and Seifert:
• [Seifert2005] Udo Seifert, Entropy production along a stochastic trajectory and an integral fluctuation theorem, Phys. Rev. Lett. 95 (2005), 4.
who understood the relevance of the self-information in this context.
The connection between statistical physics and evolutionary biology is discussed here:
• [Sella2005] G. Sella and A.E. Hirsh, The application of statistical physics to evolutionary biology, Proc. Nat. Acad. Sci. USA 102 (2005), 9541–9546.
and the ‘fitness flux theorem’ is derived in
• [Mustonen2010] V. Mustonen and M. Lässig, Fitness flux and ubiquity of adaptive evolution, Proc. Nat. Acad. Sci. USA 107 (2010), 4248–4253.
Schrödinger’s famous discussion of the physical nature of life was published here:
• [Schrödinger1944] E. Schrödinger, What is Life?, Cambridge University Press, Cambridge, 1944.

Okay, this is all good and impressive, but it still doesn’t resolve Loschmidt’s paradox. How can one explain irreversible thermodynamics from time-symmetric fundamental laws?
This post is not trying to explain that paradox, and I would not personally have chosen the title ‘The Mathematical Origin of Irreversibility’, because that suggests otherwise.
That’s right, it’s not about this paradox, especially because in the thermodynamical context this kind of Markov dynamics does not describe closed systems: the transitions are induced by a “bath” which you choose not to describe explicitly. So there’s lots of information being discarded from the very start (it’s a “mesoscopic” description) and therefore this theorem can’t teach anything about “fundamental laws”. (Incidentally, “discarded information” was also Boltzmann’s answer to Loschmidt: the Stosszahl Ansatz discards pair correlations between particles).
But suppose you’re happy with that (Loschmidt not in the room?), and ask “whence irreversibility” in this context. In other words, can you tell which trajectories contribute to the mean growth of entropy, and why? The answer is in the theorem: the entropy-producing trajectories are the “skew” ones, those which undergo transitions even though
even though  . When this happens, entropy grows.
. When this happens, entropy grows.
That's what I mean with "origin", not something related to "fundamental laws". Any suggestion for a better name?
It is interesting to connect this to Loschmidt’s paradox and see where we can go with the connection and what the fluctuation theorem can say in these regards, definitely not trying to criticize your post. It would also be interesting if we can derive an analogous theorem from a quantum probability perspective and see what this has anything more “fundamental” to say about the “origin” of “irreversibility” — seeing as how the Fluctuation theorem is derived from a classical probability perspective.
One more point which people often make, in connection with the Loschmidt paradox. For a random variable (such as
(such as 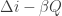 , as above) to satisfy the integral fluctuation theorem
, as above) to satisfy the integral fluctuation theorem
and therefore obey
it is necessary that some paths have
have
i.e. are "second-law violating"! They are exponentially suppressed, but still, they must be there!
So in a way (and with considerable hindsight) Loschmidt was right: "second-law violating" paths ( ) are essential to the second law (
) are essential to the second law (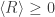 )!
)!
I work a lot with fluctuation theorems in stochastic processes and I found Matteo’s post a neat (and precise) synthesis, thanks a lot!
I’d like to mention an interesting fact, also related to Loschmidt’s paradox. Fluctuation theorems were originally conceived in the framework of *deterministic* dynamical systems (at the beginning of ’90s) and – a few years later – they were imported in the realm of (markovian and not only) stochastic processes. The quantity which satisfies the theorem in deterministic systems is the phase space contraction rate: this means that a system which conserves phase space (e.g. a Hamiltonian system) is not even a candidate for the theorem. (Very) roughly speaking, the idea is that one does not study irreversibility of a closed determinstic system, but only of an open one, which (being a portion of a closed – Hamitlonian – one) has some continuous “leak” of information which implies some production of entropy. Still one may encounter the paradox: models of deterministic systems exist which have time-reversible microscopic equations and a phase space contraction rate whose average is positive and its fluctuations satisfy the fluctuation theorem. An example is a classical molecular fluid under stationary shear and “thermostatted” in order to avoid heating. There one may “see the paradox at work” in its full glory [see for instance Phys. Rev. E 50, 1645–1648 (1994) ].
Of course when a paradox is formalized in mathematical terms, it evaporates: one can see the “error” and solve it. Unfortunately the solution is not simple. It basically involves dynamical instability (chaos – ie positivity of some lyapunov exponents – is certainly sufficient but there is still a debate on its necessity), and singularity of phase space density. Dynamical instability explains that two trajectories which are one the time-reversed of the other are both solutions of the equation of motion, but if one small piece of the first is dynamically stable, the time-reverse corresponding small piece of the other is unstable and this eventually lead to very different “path densities” in phase space: trajectories producing entropy are much more probable than trajectories violating the 2nd principle. The time-reversal symmetry of microscopic equations of motion is somehow not satisfied by evolution of density in phase space, thanks to the fact that such a density in a phase-space-contracting system tends to become singular (fractal), because of contraction. I am sure that an expert of dynamical systems could explain it much better, my expertise is the stochastic realm which is not really interested to the issue for the reason explained by Matteo and John in their replies. Hopefully the reference above [and a nice review by Evans and Searles, Advances in Physics 51, 1529 (2002) ] can shed some light on the issue.
Okay, having fixed some typos (and deleted discussion of those typos), I can now try to understand what Matteo was actually saying. By the way, I’m using the obvious trick to keep the discussion from getting very skinny, which I encourage others to do too, at least for substantial comments.
Matteo wrote:
Let me expand on this to make sure I understand it, and maybe help some other people understand it.
Suppose a random variable has the property that the mean of
has the property that the mean of 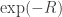 is 1:
is 1:
Since the logarithm function is concave, the logarithm of the mean is greater than or equal to the mean of the logarithm.
So, logarithm of 1 is greater than or equal to the mean of the logarithm of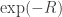 .
.
In other words, 0 is greater than or equal to the mean of .
.
In other words, the mean of is nonnegative:
is nonnegative:
On the other hand, can’t be positive everywhere, or
can’t be positive everywhere, or 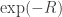 would be less than 1 everywhere, which would imply
would be less than 1 everywhere, which would imply
contradicting our assumption.
In short: if
then the mean of is ≥ 0 but
is ≥ 0 but  can’t be > 0 everywhere.
can’t be > 0 everywhere.
(This is almost what you said above, but it turns out that it’s really only necessary that some paths have , not
, not  . Aren’t mathematicians annoying?)
. Aren’t mathematicians annoying?)
So:
The integral fluctuation theorem simultaneously implies that entropy can’t decrease on average, and that it has a chance of not increasing.
Neat!
Correct, but let’s not forget that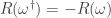 ! (As in the appendix, dagger denotes time-reversal.) So whenever
! (As in the appendix, dagger denotes time-reversal.) So whenever  takes a given positive value, it actually also take the opposite value for some other path! The point is that the probability of the latter is exponentially smaller that that of the former, according to the detailed fluctuation theorem.
takes a given positive value, it actually also take the opposite value for some other path! The point is that the probability of the latter is exponentially smaller that that of the former, according to the detailed fluctuation theorem.
I am not a mathematician so I cannot appreciate the mathematical significance of all of this but from a general perspective it doesn’t seem very enlightening to me.
It’s a bit like if we model a cow by a sphere and a moon by a sphere we can discover that the same equation for volume applies to them both.
What I mean by this is if we only focus on the irreversibility of simple models of irreversible computation and irreversible evolution then we can find connections but those seem to be more due to those simplifications then the real similarity between the processes.
For example in the real world fitness of almost every population in the history of Earth dropped to zero after some time. So in this context their evolution was not only reversible it was reversed completely.
In fact I can state a theorem similar to the one about the positive fitness flux though with an opposite conclusion. If we start with some initial population with a certain initial fitness it’s fitness will decrease to zero in a finite time and that in general fitness decreases except for the rare periods when it doesn’t. This theorem has a very strong empirical support and unlike the “positive flux” one it applies to the real world instead of an idealized model of evolution.
Now, that’s not a comment I expected! Are you saying that species don’t generally evolve to improve their fitness? That the opposite has “very strong empirical support”? Are you making some subtle point about evolution here (that it’s not monotonous, that all species eventually get extinct, something along this line), or are you plainly denying natural selection and evolution?
The point I’m making is that while evolution itself does improve fitness that certainly doesn’t mean that fitness in the real world keeps improving. On the contrary in most cases improvements due to evolution prove insufficient and species go extinct.
If you look at the history of life on Earth almost all species that ever existed are now extinct. Their evolution failed to keep up with changes in natural environment and fitness of their populations reached zero. Only a very small fraction managed to survive in some form to this day.
Homo sapiens is a good example, we know of many early branches of homo yet all but one of them are now extinct. Evolution of neanderthals failed, the fitness of their population reached zero and they are gone. Ours may very well do the same eventually.
So while evolution as an abstract process may be irreversible, the gains in fitness due to evolution in the real world are very much reversible and in most (and possibly all) cases only temporary.
Oh well, I’m happy enough if I can understand that. The “real world” is not something we scientists can say much about, can we? So we do models, and understand aspects of it. And that’s good, right?
I think it’s worth pondering why Arrow’s observation doesn’t contradict the results Matteo presented… since that will help us go further.
Matteo’s results are about time-translation-invariant Markov processes. So, they’re a good model of games where organisms randomly choose other organisms to compete against and randomly succeed (get to reproduce) or fail (don’t get to reproduce), with probabilities that depend on who is playing the game but don’t change with time.
In such situations, the fittest organisms will, on average, take over.
This is the idea behind the ‘fitness flux theorem’ presented here, as far as I can tell.
However, in the real world the assumption of time translation invariance is only a good approximation in limited regimes. There are occasional ‘crises’, like ice ages and meteor impacts and colliding continents. When these occur, what used to be the fittest organisms are no longer the fittest! So, we have extinction events.
We could model this by dropping the assumption of time translation invariance. That would be fun to try.
Or, over very long time scales, we might model these occasional crises as occurring randomly, and fold them into the overall Markov process!
In reality this Markov process would still not be time translation invariant. For example, asteroid impacts have gradually become less and less common over the last 3.5 billion years.
But we could still learn something by looking at models where this Markov process is time translation invariant. What we’d see is that very rare random extinction events would make it very likely that a given sample path (‘history of the world’) saw fitness rise, crash, rise, crash, etc. But for the average over all these sample paths, fitness would rise!
There’s a lot more to think about here…
I did present the fitness-flux theorem in the time-translation invariant case, but that was just for simplicity; you don’t need to assume that (the authors of the paper on the fitness-flux theorem do not, I think, and in the proof of the fluctuation theorem I don’t either). I think the point is more that the inequality does not in itself tell you that fitness must improve over time: that depends on the actual
does not in itself tell you that fitness must improve over time: that depends on the actual  . But when entropy does decrease, meaning that the population actually adapts to its environment, then it must be in the direction of positive fitness flux.
. But when entropy does decrease, meaning that the population actually adapts to its environment, then it must be in the direction of positive fitness flux.
I don’t follow that. It seems that if the environment changes, what counts as fit changes, so the definition of Phi changes.
What happens in an oscillating environment, where the population keeps adapting, then adapting back?
I just remembered this paper.
Click to access anzf40-185.pdf
It has simulations of populations constantly adapting to a changing environment, and sometimes going extinct.
The fitness flux is defined as a sum over all transitions along the process. For each transition
is defined as a sum over all transitions along the process. For each transition  , it compares the forward and backward transition rates *at time
, it compares the forward and backward transition rates *at time  *. You’re right that if the environmental conditions change along the process, what counts as fit also change; what matters is the fitness variation at each transition. In other words, in a changing environment
*. You’re right that if the environmental conditions change along the process, what counts as fit also change; what matters is the fitness variation at each transition. In other words, in a changing environment 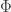 depends on the actual times at which the transitions took place: a transition that increases fitness at some time may not increase fitness at some other time. But did I get your question right, Graham?
depends on the actual times at which the transitions took place: a transition that increases fitness at some time may not increase fitness at some other time. But did I get your question right, Graham?
Matteo wrote:
You may not consider these separate, but besides thermodynamics and biological evolution I like to think about two other examples: game theory and machine learning.
I talked about evolutionary game theory and statistical mechanics in part 12 and part 13 of the information geometry series. I want to dramatically improve what I said there based on your post here.
You can think of evolutionary game theory as being about biological evolution, where a mixed strategy is a mixture of genotypes and mixed strategies change as genotypes undergo natural selection. But you can also think of it as being about economic evolution, where players gradually change their mixed strategies in a deliberate attempt to optimize something. A lot of ideas from statistical mechanics still apply, but this also leads to new models that don’t make sense for biological evolution. A good very easy introduction is here:
• William H. Sandholm, Evolutionary game theory, 12 November 2007.
Sandholm mentions some other places where the same ideas show up:
(I think he includes references, which I deleted here because it’s annoying to see things like [13,14] when you can’t see what they refer to.)
He mentions computer science, but it’s really more specifically machine learning that tries to combine ideas from evolutionary biology and statistical mechanics to develop systems that optimize their predictive power. So, it would be nice to see what the detailed fluctuation theorem has to say in economics and machine learning.
I was looking for a semi-popular book on life and nonequlibrium thermodynamics, and I discovered this book:
• Eric D. Schneider and Dorion Sagan, Into the Cool: Energy Flow,Thermodynamics and Life, University of Chicago Press, Chicago, London, 2005.
I read a review by Craig Callendar of the philosophy department at U.C. San Diego. It mentions Crooks’ fluctuation theorem, so I thought I’d quote part of it. It’s slightly relevant to what we’re talking about:
Thanks for the quote! I should have said somewhere that the “detailed fluctuation theorem” and “Crooks theorem” are essentially the same, just like the “integral fluctuation theorem” and the “Jarzynski identity”.
Callendar remarks that these have not been applied to life or economics. Not so anymore! The “fitness flux theorem” is an example of a non-physics application, and I claim there will be more. As I said in the post, the fluctuation theorem is really a universal mathematical property of Markov processes; it’s like the central limit theorem, if you wish: it’s so universal that it’s bound to appear everywhere.
By the way, it’s only almost always true that “Nature abhors a gradient”, as stated on the backcover of this book. In some cases, (which of course do not spoil the relevance of the book’s main point!) dissipative dynamics can actually produce a gradient from no gradient! If you’re interested, I’ve discussed this surprising effect (which you can think as a version of the famous “ratchet effect”) in [arXiv:1206.3441].
This summer I’ve read a nice book by J. Scales Avery, the title is “Information Theory and Evolution”, by World Scientific. It is semipopular and perhaps gets close to what John is looking for. The book describes in a very pleasant (and never trivial) way many phenomena (from biology at all size/time scales, to culture, technology, economy etc.) where the same picture emerges: order in a subsystem grows, while in the total system it cannot grow. However it is not very satisfying in the few paragraphs where (physics/mathematics) formalism is used: the observations are repeated in information language, but there are no hints on how to get a predictive theory.
In summary, there is a powerful principle saying that in a closed system order cannot grow, nevertheless we are surrounded by open systems where order grows. And the only thing we are able to say is “well, there is no contradiction”…. This is frustrating.
With regard to the notions of fittingness and gradients of one sort and another, I am curious about the origins of concerted action. If this comment is way off track, would you kindly ignore it or simply delete it.
Consider that when you take a stroll in the woods, metric tons of raw matter around you are acting in concert, there is a high degree of fittingness on many meta-levels, everything is mutually finding its proper angle of repose and surprisingly, for great deal of matter, that angle is nearly vertical. There is consensus, a congruous entwining of energy paths, and a multiplicity of ‘formal’ agreements that are both dynamic and enduring. You belong in this scene to the very level of complex DNA chemistry that is resonant within the world around you.
Now, in an ideal gas at maximal entropy, I would expect each molecule to be traveling on its own unique trajectory, each with its own information theoretic distinction. There would be no concerted action, no consensus as to path. Does the trend toward increasing entropy and the final state thereof allow us to roughly characterize the nature of energy? That is, if there is utility in the notion ‘nature abhors a gradient’ is there also some utility in the notion that energy eschews pathways?
If we tentatively accept that idea, then how is it possible to view the world about us as resulting from the evolving ‘chemistry’ and entwinement of energy pathways?
‘Into the Cool: Energy Flow, Thermodynamics and Life’ sounds very similar in scope to Howard T Odum’s book, ‘Environment, Power and Society’, published in 1971, both in search of general organizing principles.
General organizing principles are useful and in that regard I am wondering if it is useful to identify some grand counterpoise to energy as being catalytic in the emergence of path. Pathways emerge on gradients, not at equilibrium. On a deep level, could path be viewed as emergent between countervailing gradients of distinction?
Matteo, thanks for the great posting which I am struggling to understand. I was encouraged when the Kolmogorov equation looked intuitive based on my interpretation of the transition rates, which is roughly (my first use of latex, bear with me:-):
However, when I read your description of them more carefully I became puzzled. If the transition rates constitute a matrix in which the off-diagonal entries are non-negative and the column sums are zero, that implies the diagonal entries are negative, which implies that the diagonal entries (at least) are not everyday probabilities.
I followed up on the “infinitesimal stochastic matrix” hotlink you provided, but the discussion there assumes physics background (Hamiltonians etc.) which I don’t have.
Is there a (hopefully simple:-) math-oriented description of these transition rates somewhere? (I’m encouraged by your section title “The mathematical fact” to believe that such a description is at least possible:-)
Thanks much!
Those gamma’s are not probabilities, but “transition rates”: they tell you how much the probability that the system is in a given state changes over time. The diagonal elements of a “infinitesimal stochastic matrix”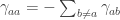 , in particular, are negative because the probability that the state remains
, in particular, are negative because the probability that the state remains  can only decrease over time—at some point or another, the system will jump to another state
can only decrease over time—at some point or another, the system will jump to another state  .
.
Thanks Matteo! I think I understand.
Or maybe not: In the master equation, it seems to me that the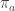 and the
and the 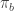 on the RHS should be switched. Am I still confused?
on the RHS should be switched. Am I still confused?
You’re right, this is a typo. Thanks for pointing it out!
Trying the latex part again w/ space before trailing dollar sign..
And once more with just the LHS..
Your problem never had anything to with the use of
$latex $
That was always fine. You don’t need a space before the trailing dollar sign, though you do need one after “latex”. The problem is that you’re writing:
\gamma_a_b
which LaTeX can’t parse. It can’t tell whether you want b to be a subscript of a, like this;
\gamma_{a_b}
which gives
or what you really want, which is to have b be a subscript of \gamma, like this:
\gamma_{ab}
which gives
Thanks John! I should have realized that my syntax was unlikely to be correct.
It didn’t help that http://www.texify.com/links.php managed to interpret it as I had intended (almost – I now see that it places the b very slightly higher(!) than the a).
Does anyone have a pointer to an online LaTeX interpreter which is decently compatible with the one used here?
Just reporting some minor typos; feel free to delete this when they’re addressed:
1. you say, near the top of the main post
… by the times at which the transitions
at which the transitions  occur …
occur …
but the following formula shows such transitions labelled with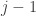 rather than
rather than 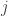 .
.
2. Some of the most recent comments above this one contain an error message “formula does not parse”.
An interesting/related paper was recently published in PRL, “Thermodynamics of Prediction” by S. Still, with Crooks as a coauthor, here is the arXiv link: http://arxiv.org/abs/1203.3271
I’ll try to explain it a bit to encourage you to read it.
Related to Jarzynski’s work and the fluctuation theorem is the idea of measuring equilibrium quantities by forcing a system out of equilibrium and observing the response, see: http://www.physics.berkeley.edu/research/liphardt/pdfs/JarzynskiTest.pdf
In Still’s paper they observe that much of the literature assumes that the driving signal is given/known explicitly, while in nature and biological systems this is most often not the case, hence they study stochastic driving signals.
The idea is that implicit in the dynamics of such a forced system is a model of its (stochastic) environment. They then ask how the quality of this model is related to thermodynamic efficiency.
How do you measure the quality of a model?
For them a good model should have predictive power and not be overly complicated. This comes down to a balance of a systems memory, namely you break it into two parts, one useful, predictive part, and the other “useless nostalgia”. It is this latter part that is related to dissipation, hence having less nostalgia is having less dissipation is having better thermodynamic efficiency.
Here is a whirlwind tour of how the paper makes this idea precise, taking many quotes straight from the paper: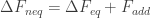


 , which is precisely the additional free energy (the KL divergence of the current distribution relative to the equilibrium one).
, which is precisely the additional free energy (the KL divergence of the current distribution relative to the equilibrium one).
“the dynamics of system are modeled by discrete time Markovian conditional state-to-state transition probabilities”
For the driving signal they assume only that its changes are governed by some probability density.
Their system is in contact with a heat bath and starts in equilibrium. It then goes through a bunch of steps where the environment forces it out of equilibrium and then it relaxes. The environment does work on the system in each driving step and heat flows at each relaxation step.
If you let it relax all the way to equilibrium any additional free energy gets dissipated as heat back to the environment. The additional free energy is given by the Kullback-Leibler divergence, or the relative entropy between the current state/distribution and the equilibrium one. The change in non-equilibrium free energy is the sum of the change in equilibrium free energy and this additional piece:
Dissipation work is given by the difference between work done on the system and the non-equilibrium change in free energy:
Excess work is given by the difference in work done on the system and the equilibrium free-energy (the work done for the quasistatic case):
The excess work minus the dissipation work gives you,
Now for the information/prediction half, which I understand even less!![I[s_{t},x_{t}]](https://s0.wp.com/latex.php?latex=I%5Bs_%7Bt%7D%2Cx_%7Bt%7D%5D+&bg=ffffff&fg=333333&s=0&c=20201002) where s is for system and x is for external signal. The ‘instantaneous predictive power’ is,
where s is for system and x is for external signal. The ‘instantaneous predictive power’ is, ![I[s_{t}, x_{t+1}]](https://s0.wp.com/latex.php?latex=I%5Bs_%7Bt%7D%2C+x_%7Bt%2B1%7D%5D+&bg=ffffff&fg=333333&s=0&c=20201002) , or the mutual information of a state at time t and the driving signal at t+1. The difference of the two is the ‘instantaneous nonpredictive information;’ “it represents useless nostalgia and provides a measure for the ineffectiveness of the implicit model.” (So memory-power=information, kidding)
, or the mutual information of a state at time t and the driving signal at t+1. The difference of the two is the ‘instantaneous nonpredictive information;’ “it represents useless nostalgia and provides a measure for the ineffectiveness of the implicit model.” (So memory-power=information, kidding)
They look at Shannon’s (symmetric) mutual information of the system state and the external driving signal, both at a certain time t, this is called the system’s ‘instantaneous memory’,
The paper then shows that this instantaneous nostalgia is proportional to the average work dissipated as t goes to t+1.
They derive a lower bound on the total dissipation and use it to refine Landauer’s principle. They then discuss this in relation to biological systems, where the systems have adapted to their environments forcing, asking if minimizing nostalgia is a factor driving things towards energetic efficiency.
This paper is more about thermodynamics and prediction (as the title suggests) than about reversibility. I don’t understand it yet, but there are hints of connections here, not only among biology, chemistry and nature, but also information and complexity (algorithmic information theory). I guess that’s why there is all the talk of Kolmogorov above. I’m new at this, and I’m sure many of you reading this have a better big picture! It seems though that in Still’s paper, a good model is about balancing complexity with predictability, and that this is done by not having any nostalgia, which doesn’t sound practical for us nostalgic humans! I would like to learn more though about mutual information in biological systems, and how some systems we understand a little bit have some ‘memory’ built in, either about their environment, or even their own dynamics.
So read the paper, it does a better job explaining itself!
I’ve really got to read this… thanks for the tantalizing summary!
I wonder if the dynamic of evolution could be modeled via an audio analogue. That is, the environmental forcing could be seen as being produced by a complex audio waveform and the genetic population modeled as a resonant surface, a complex Chladni plate.
Would the resonance of that surface produce a complimentary chance in the driving signal? This seems to be the case in biological systems.
[…] The Mathematical Origin of Irreversibility (johncarlosbaez.wordpress.com) […]
The properties of the Radon-Nikodym derivative are invoked all through the proof, and understanding the end result really seems to come down to understanding this object. Can you give any intuition about it?
If you have a measure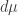 you can get another measure by multiplying it by a function
you can get another measure by multiplying it by a function  :
:
Conversely, under some conditions you can figure out knowing the measures
knowing the measures 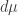 and
and 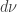 . This trick is called the Radon-Nikodym derivative because if you just follow your nose it looks like a derivative
. This trick is called the Radon-Nikodym derivative because if you just follow your nose it looks like a derivative
It’s really more like division: the measure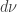 divided by the measure
divided by the measure 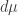 is the function
is the function  .
.
If this is too abstract for you, imagine is the usual thing that shows up in integrals and define
is the usual thing that shows up in integrals and define
for functions and
and  . Then the Radon-Nikodym derivative at the point
. Then the Radon-Nikodym derivative at the point  is
is
whenever this exists, that is, whenever you’re not dividing by zero.
I’m stating everything in a way that leaves out the technical fine print that’s needed for an actual theorem. For that, try Wikipedia. But you said you wanted intuition, and the intuition is a lot simpler than the Wikipedia article makes it seem.
Hi there
This has been on my “to read” list for ages and I finally got to it. But I’m having trouble seeing how the “immediate consequence”
follows from
Is there any chance you could sketch out the derivation a little, or just point me towards a reference?
I tried searching for “integral fluctuation theorem”, and found this, which seems to derive something similar, but it’s written in very different notation and it’s hard to connect it to what you’ve written here.
I don’t know if Matteo is listening, but I’ll think about this while I’m proctoring a 3-hour real analysis final today.
Thanks, I really appreciate that!
So, we have a random variable and we’re trying to show
and we’re trying to show
implies
For starters, let’s try an example. Suppose can only equal 1 or -1. Say the probability it equals 1 is
can only equal 1 or -1. Say the probability it equals 1 is 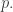 Then this probability is
Then this probability is  times the probability that
times the probability that  equals -1, so
equals -1, so
so
So, the mean value of is
is
So it’s not 1. So either I’m making a dumb mistake or the claim needs to be fixed somehow. I think I can show that in general
implies
or more generally, if we have a probability density function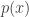 :
:
and
then
But I don’t know if this is the right way to fix the claim: replace the equation with an inequality. I have a feeling that changing things a bit could give us an equation.
I’ve got it.
It’s rather than
rather than 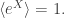 Then your example works, and the proof of the general case is quite simple:
Then your example works, and the proof of the general case is quite simple:
I found the proof in this paper:
D. M. Carberry, S. R. Williams, G. M. Wang, E. M. Sevick, and Denis J. Evans
The Kawasaki identity and the Fluctuation Theorem
J. Chem. Phys. 121, 8179 (2004); http://dx.doi.org/10.1063/1.1802211
Click to access Carberry_JCP121_8179(2004).pdf
Oh, great! Yay!
So in the end it was a mere typo… I’ll see if it actually afflicts the original post, and fix it if it does. Thanks for solving this mystery—I’d gotten distracted from it. And thanks for providing the proof.
It looks like the original post got the sign right.
Would this be a reasonable picture of the idea:
Start with a row of cups each containing some amount of liquid.
Let an exchange be the following: randomly select a source cup and a destination cup and some quantity less than the amount in the source cup. Move the quantity between the two cups.
Let a series of exchanges be a mixing.
The rate of mixing intuitively is expressed by the skewness. (If the skewness were zero all the amounts would be constant.)
The result can be stated this way: the information difference between the starting and ending states is always non-negative and a function of the mixing rate.
Also, the so-called “Data Processing Inequality” seems relevant:
Consider a Markov chain X -> Y -> Z with Z = f(Y). Then I(X, Z) is less than or equal to I(X, Y). [I is mutual information.]
Lastly, there are questions in the comments regarding the time-invariance of the transition matrix and how that limits the result. Would it be possible to define a “larger” transition matrix where each state S would be replaced by a series of states (S, t) for each time t? The purpose being to construct a constant transition matrix and thereby applying the theorem to seemingly time-variant processes?
I initially visualized this in a similar way but I’m not sure that it is a valid picture. I wonder if the author could comment?
See also Matteo Smerlak’s guest post on John Baez’s blog Azimuth. […]
Christopher Jarzynski is famous for discovering the Jarzynski equality. We’ve had a good quick explanation of it here on Azimuth:
• Eric Downes, Crooks’ Fluctuation Theorem, Azimuth, 30 April 2011.
We’ve also gotten a proof, where it was called the ‘integral fluctuation theorem’:
• Matteo Smerlak, The mathematical origin of irreversibility, Azimuth, 8 October 2012.
It’s a fundamental result in nonequilibrium statistical mechanics—a subject where inequalities are so common that this equation is called an ‘equality’.
Two days ago, Jarzynski gave an incredibly clear hour-long tutorial on this subject, starting with the basics of thermodynamics and zipping forward to modern work. With his permission, you can see the slides here:
• Christopher Jarzynkski, A brief introduction to the delights of non-equilibrium statistical physics.
Also try this review article:
• Christopher Jarzynski, Equalities and inequalities: irreversibility and the Second Law of thermodynamics at the nanoscale, Séminaire Poincaré XV Le Temps (2010), 77–102.
[…] This introduction is elementary and excellent. The results can also be framed as a consequence of a more general result based merely on the Markov property. To go deeper, start reading Crook’s thesis […]
Thanks for a really interesting article, Matteo.
I’m trying to illustrate these theorems for myself with a toy example, and I’m having some trouble. Perhaps someone might be able to point out the problem with my math.
Suppose we have a system with two states, and
and  , where
, where  and
and  . From the detailed balance condition
. From the detailed balance condition  , we know that the stationary probabilities are
, we know that the stationary probabilities are  and
and  .
.
Suppose we begin the process in state , (i.e.
, (i.e. 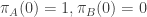 ) and let it run for an infinitely long period of time. What will the skewness and variation in self-information be when we next examine the process? There are two cases to consider:
) and let it run for an infinitely long period of time. What will the skewness and variation in self-information be when we next examine the process? There are two cases to consider:
If the system is in state , then the skewness
, then the skewness 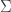 will be
will be
and
This case occurs with probability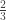 .
.
If the system is in state , then the skewness
, then the skewness 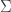 will be
will be
and
This case occurs with probability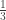 .
.
Then we have:
I would be the first to assume that the problem lies somewhere in my arithmetic. But I checked it by hand and with simulation, and can't find the flaw. And if it is an arithmetic error, it's not a simple sign error: I checked all of and still couldn't get it to come out right. But I'd still be grateful to be proven wrong.
and still couldn't get it to come out right. But I'd still be grateful to be proven wrong.
Or maybe there's an issue with the definition of skewness? In particular, doesn't seem to be well-defined since
doesn't seem to be well-defined since  is not defined. So I just interpreted
is not defined. So I just interpreted 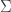 to be sum of the lograthmic ratio of the reverse and forward transition rates, over all transitions. But maybe that's wrong?
to be sum of the lograthmic ratio of the reverse and forward transition rates, over all transitions. But maybe that's wrong?
Thanks in advance for any light anyone might be able to shed here.
I’ve emailed Matteo and asked him to look at your question.
Thanks John!
Hi Patrick!
The fluctuation theorem involves an average over trajectories, not over states. To check it explicitly in this example, you would have to consider a sum with infinite many terms (and not two as you write), each one corresponding to a possible trajectory of the system.
I hope this helps.
Hi Matteo,
Thanks very much for the reply! I think I’m still stuck, though. I get that the expectation is over all trajectories, but it seems to me that in a two state system, the sum over trajectories can still be computed by grouping the trajectories according to their terminal states.
This should work because, for reasons outlined above, and
and 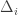 depend only on the terminal state. (This is of course not true in general– for three or more states you can have loops that make net contributions to the skewness.)
depend only on the terminal state. (This is of course not true in general– for three or more states you can have loops that make net contributions to the skewness.)
So if and
and 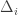 depend only on the terminal state, then you should be able to simply figure out how much probability mass ends up at each state, and sum over states. Each state collects an uncountably infinite number of trajectories, sure, but they all carry the same contribution to the sum so you shouldn’t have to keep track of them individually. At least, not in the two state case.
depend only on the terminal state, then you should be able to simply figure out how much probability mass ends up at each state, and sum over states. Each state collects an uncountably infinite number of trajectories, sure, but they all carry the same contribution to the sum so you shouldn’t have to keep track of them individually. At least, not in the two state case.
But let me see if I can simplify the argument even further. Every trajectory ends either in state
ends either in state  or state
or state  . If it ends in
. If it ends in  , its contribution to the sum is
, its contribution to the sum is 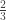 , weighted by whatever the probability density is. If it ends in
, weighted by whatever the probability density is. If it ends in  , then its contribution is also
, then its contribution is also 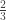 weighted by its density. So no matter what measure we assign to the trajectories, it’s hard to see how we can get to unity when integrating over them.
weighted by its density. So no matter what measure we assign to the trajectories, it’s hard to see how we can get to unity when integrating over them.
I’ve also tried Monte Carlo simulations to check my work. In that case I’m explicitly sampling trajectories, but I’m still getting the same answer.
Anyway, thanks again for your response to a comment on a five year old blog post, and my apologies if I’m missing something obvious.
Sorry, the last comment had formatting issues.
Ok, I think I figured it out. The problem actually arises from the fact that the initial distribution is degenerate. To see how this comes up, recall the setup above where we start in state
is degenerate. To see how this comes up, recall the setup above where we start in state  and run the process to stationarity. Now in the penultimate step in the derivation of the integral fluctuation theorem, we have:
and run the process to stationarity. Now in the penultimate step in the derivation of the integral fluctuation theorem, we have:
If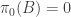 , then
, then  is undefined for any trajectory
is undefined for any trajectory  such that
such that  . One might hope to sweep this detail under the rug, since
. One might hope to sweep this detail under the rug, since  implies
implies  , leaving our sum undefined only on a set of measure zero. But notice how the RHS expands:
, leaving our sum undefined only on a set of measure zero. But notice how the RHS expands:
where just collects every term in
just collects every term in 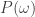 except the probability of starting in the initial state
except the probability of starting in the initial state 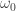 . Then the RHS reduces to:
. Then the RHS reduces to:
So it looks like these measure-zero trajectories are still sneaking in to contribute to the sum, at least if you define the sum for degenerate choices of to be the limit of the sum as
to be the limit of the sum as  approaches the desired initial conditions. Or something like that? In either case, summing over all trajectories (and not merely those that begin in state
approaches the desired initial conditions. Or something like that? In either case, summing over all trajectories (and not merely those that begin in state  ) gives me the correct answer. This strikes me as somewhat spooky, but it seems to work.
) gives me the correct answer. This strikes me as somewhat spooky, but it seems to work.
Anyway, thanks again Matteo and John for revisiting this!
[…] The more recent Fluctuation Relation (FR)1 and its corollary the Integral Fluctuation Relation (IFR), which have been discussed on this blog in a remarkable post by Matteo Smerlak.
[…] Relation (FR)1 and its corollary the Integral FR (IFR), that have been discussed on this blog in a remarkable post by Matteo Smerlak […]