Resource Convertibility (Part 2)

guest post by Tobias Fritz

In Part 1, I introduced ordered commutative monoids as a mathematical formalization of resources and their convertibility. Today I’m going to say something about what to do with this formalization. Let’s start with a quick recap!

Definition: An ordered commutative monoid is a set A equipped with a binary relation \geq, a binary operation +, and a distinguished element 0 such that the following hold:

• + and 0 equip A with the structure of a commutative monoid;

• \geq equips A with the structure of a partially ordered set;

• addition is monotone: if x\geq y, then also x + z \geq y + z.

Recall also that we think of the x,y\in A as resource objects such that x+y represents the object consisting of x and y together, and x\geq y means that the resource object x can be converted into y.

When confronted with an abstract definition like this, many people ask: so what is it useful for? The answer to this is twofold: first, it provides a language which we can use to guide our thoughts in any application context. Second, the definition itself is just the very start: we can now also prove theorems about ordered commutative monoids, which can be instantiated in any particular application context. So the theory of ordered commutative monoids will provide a useful toolbox for talking about concrete resource theories and studying them. In the remainder of this post, I’d like to say a bit about what this toolbox contains. For more, you’ll have to read the paper!

To start, let’s consider catalysis as one of the resource-theoretic phenomena neatly captured by ordered commutative monoids. Catalysis is the phenomenon that certain conversions become possible only due to the presence of a catalyst, which is an additional resource object which does not get consumed in the process of the conversion. For example, we have

\text{timber + nails}\not\geq \text{table},

\text{timber + nails + saw + hammer} \geq \text{table + saw + hammer}

because making a table from timber and nails requires a saw and a hammer as tools. So in this example, ‘saw + hammer’ is a catalyst for the conversion of ‘timber + nails’ into ‘table’. In mathematical language, catalysis occurs precisely when the ordered commutative monoid is not cancellative, which means that x + z\geq y + z sometimes holds even though x\geq y does not. So, the notion of catalysis perfectly matches up with a very natural and familiar notion from algebra.

One can continue along these lines and study those ordered commutative monoids which are cancellative. It turns out that every ordered commutative monoid can be made cancellative in a universal way; in the resource-theoretic interpretation, this boils down to replacing the convertibility relation by catalytic convertibility, in which x is declared to be convertible into y as soon as there exists a catalyst which achieves this conversion. Making an ordered commutative monoid cancellative like this is a kind of ‘regularization’: it leads to a mathematically more well-behaved structure. As it turns out, there are several additional steps of regularization that can be performed, and all of these are both mathematically natural and have an appealing resource-theoretic interpretation. These regularizations successively take us from the world of ordered commutative monoids to the realm of linear algebra and functional analysis, where powerful theorems are available. For now, let me not go into the details, but only try to summarize one of the consequences of this development. This requires a bit of preparation.

In many situations, it is not just of interest to convert a single copy of some resource object x into a single copy of some y; instead, one may be interested in converting many copies of x into many copies of y all together, and thereby maximizing (or minimizing) the ratio of the resulting number of y‘s compared to the number of x‘s that get consumed. This ratio is measured by the maximal rate:

\displaystyle{ R_{\mathrm{max}}(x\to y) = \sup \left\{ \frac{m}{n} \:|\: nx \geq my \right\} }

Here, m and n are natural numbers, and nx stands for the n-fold sum x+\cdots+x, and similarly for my. So this maximal rate quantifies how many y’ s we can get out of one copy of x, when working in a ‘mass production’ setting. There is also a notion of regularized rate, which has a slightly more complicated definition that I don’t want to spell out here, but is similar in spirit. The toolbox of ordered commutative monoids now provides the following result:

Rate Theorem: If x\geq 0 and y\geq 0 in an ordered commutative monoid A which satisfies a mild technical assumption, then the maximal regularized rate from x to y can be computed like this:

\displaystyle{ R_{\mathrm{max}}^{\mathrm{reg}}(x\to y) = \inf_f \frac{f(y)}{f(x)} }

where f ranges over all functionals on A with f(y)\neq 0.

Wait a minute, what’s a ‘functional’? It’s defined to be a map f:A\to\mathbb{R} which is monotone,

x\geq y \:\Rightarrow\: f(x)\geq f(y)

and additive,

f(x+y) = f(x) + f(y)

In economic terms, we can think of a functional as a consistent assignment of prices to all resource objects. If x is at least as useful as y, then the price of x should be at least as high as the price of y; and the price of two objects together should be the sum of their individual prices. So the f in the rate formula above ranges over all ‘markets’ on which resource objects can be ‘traded’ at consistent prices. The term ‘functional’ is supposed to hint at a relation to functional analysis. In fact, the proof of the theorem crucially relies on the Hahn–Banach Theorem.

The mild technical mentioned in the Rate Theorem is that the ordered commutative monoid needs to have a generating pair. This turns out to hold in the applications that I have considered so far, and I hope that it will turn out to hold in most others as well. For the full gory details, see the paper.

So this provides some idea of what kinds of gadgets one can find in the toolbox of ordered commutative monoids. Next time, I’ll show some applications to graph theory and zero-error communication and say a bit about where this project might be going next.

• Resource convertibility: part 3.

This entry was posted on Friday, April 10th, 2015 at 1:00 am and is filed under chemistry, mathematics, networks, physics. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

5 Responses to Resource Convertibility (Part 2)

  1. lee bloomquist says:
    10 April, 2015 at 10:14 pm

    Tobias,

    You wrote: “In economic terms, we can think of a functional as a consistent assignment of prices to all resource objects.” I’m pretty sure you don’t mean to, but I think you are getting close to politics. For an overview, A (below) links to a Nova video that you might like. Or dislike. But I’m guessing the former.

    According to the video, mathematical economists have so far ruled the roost in determining policy. But now behavioral economists have more success in explaining the economy. Some mathematical economists don’t like this. One is even quoted as saying that he stopped his subscription to The Economist because it reports findings in behavioral economics.

    Question:

    Who would be more inclined to apply your resource theory as it stands right now– mathematical economists or behavioral economists?

    Behavioral economics is based on social science. There is now in D.C. a struggle between belief systems and science, to the extent that defunding social science is once again on the political agenda. See B, which links to a proposal to Congress that all social science be defunded.

    In the paper linked to C, social science has in the past changed its mind about racism. After the change, an agenda to defund social science is evident. For example about twenty years ago, when I was working as an industrial researcher, I overheard the topic of defunding all social science discussed at a table at a restaurant in D.C.

    Today there is an urgent need for policy to address the resources of food and water. Think of California.

    From pollution, water changes from a resource for life into a non-potable resource for things like cooling systems.

    From inefficient use, food changes from a resource for humans into a resource for other forms of life. And about a third of each year’s production is wasted. (D)

    So when this amount of food is being wasted, is the cause of people starving to death on the planet a more fitting subject for mathematical economics or behavioral economics? Which field is probably better for studying greed?

    I do hope behavioral economists become interested in applying your work. They might be able to use your theorems in their political struggle against the mathematical economists.

    A:
    http://www.pbs.org/wgbh/nova/body/mind-over-money.html

    B:
    http://www.huffingtonpost.com/scott-atran/social-science-in-the-national-interest_b_2887840.html

    C:
    http://scholarship.law.duke.edu/cgi/viewcontent.cgi?article=2916&context=dlj

    D:
    http://www.worldfooddayusa.org/food_waste_the_facts

    Reply
    • Tobias Fritz says:
      13 April, 2015 at 1:56 am

      Whoops, I only see this comment now — I’m sorry to not have replied earlier! I’ve been a bit distracted by our entropy workshop.

      Your thoughts are extremely interesting to me. Using the toolbox of ordered commutative monoids in economics is an eventual goal that I have. But there’s a long way to go! For now, I can say a bit about how this project relates to behavioral vs ‘rational agent’ economics. I think there are mainly two ways of applying resource-theoretic ideas economically:

      1) As an entire society, we can try to study how much well-being we can extract from our resources, or conversely how much of our natural resources we need to consume in order to generate a given amount of well-being. The toolbox of theorems that I am developing should apply to this type of question. The theory does not say anything about how the optimum is to be achieved; it might be possible to do so using a market-based economy, or it might require a planned economy.

      2) An individual agent, such as a person or a company, can be concerned with their own resources and how much of them they need in order to achieve certain goals. Resource-theoretic ideas apply here as well; in fact, they are already being applied whenever one uses linear programming to study resource allocation. If you want to classify this according to rational-agent vs behavioral economics, it will belong to the former. In particular, my paper also discusses the utility theorem, which is the basis of the theory of rational agents.

      So, I’m afraid that what I’m doing will not help behavioral economics in any immediate way. But in an ideal world, it would help us achieve the transition to sustainability.

      Your links A-D are very interesting! I need to find time to study them in detail and might get back to you here with further comments or questions.

      Reply
  2. Marco says:
    12 April, 2015 at 8:03 pm

    TPTB want to hear what they want to hear and nothing else. their preference for ‘mathematical’ economists over ‘social’ economists is all about conclusions, not methods.
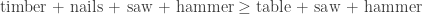
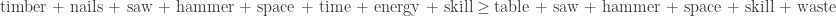
    The difference in conclusions is largely a result of the starting assumptions, which in the case of ‘mathematical’ (neo-classical) economists are chosen in order to give results agreeable to TPTB.
    So both kinds of economists will use these monoids to reach the conclusions they want to reach.
    eg.
    \text{timber + nails + saw + hammer} \geq \text{table + saw + hammer}
    or
    \text{timber + nails + saw + hammer + space + time + energy + skill} \geq \text{table + saw + hammer + space + skill + waste}

    Reply
    • Tobias Fritz says:
      13 April, 2015 at 2:03 am

      Yes, I think that’s about right. If anything, I would hope that ordered commutative monoids can help us to make the difference in starting assumptions more explicit, which may help us to figure out which starting assumptions are realistic and which ones ignore aspects that are relevant to the problem.

      (And just to be clear: the theory of ordered commutative monoids is not descriptive! In other words, it is not a theory of what happens in the economy. Rather, it is a theory of what can be made to happen in principle, which allows for informed decision-making.)

      Reply
  3. Applied Category Theory Course: Resource Theories | Azimuth says:
    12 May, 2018 at 1:49 am

    We are lucky to have Tobias in our course, helping the discussions along! He’s already posted some articles on resource theory here on this blog. We’re having fun bouncing between the relatively abstract world of monoidal preorders and their very concrete real-world applications to chemistry, scheduling, manufacturing and other topics. Here are the lectures so far:

    • Lecture 18 – Chapter 2: Resource Theories
    • Lecture 19 – Chapter 2: Chemistry and Scheduling
    • Lecture 20 – Chapter 2: Manufacturing
    • Lecture 21 – Chapter 2: Monoidal Preorders
    • Lecture 22 – Chapter 2: Symmetric Monoidal Preorders

    Reply

You can use Markdown or HTML in your comments. You can also use LaTeX, like this: $latex E = m c^2 $. The word 'latex' comes right after the first dollar sign, with a space after it.

This site uses Akismet to reduce spam. Learn how your comment data is processed.