My grad students and I have been using a lot of category theory in our work on networks in engineering, chemistry and biology. So I decided to teach an introductory course on category theory, and it was surprisingly popular: 25 grad students registered for it! Clearly there’s a lot of interest in the subject, and we don’t regularly teach a course on it at U. C. Riverside.
Here are the notes from my course. In my earlier fall Fall 2015 seminar, I had tried to explain how category theory unifies mathematics, without getting into lots of technical details. This time I tried to give a systematic introduction to the subject, leading up to a little taste of topos theory. But many proofs were offloaded to another more informal seminar, for which notes are not available.
When I started teaching this course, I imagined that the notes might someday grow into a book I’d always dreamt of: an introduction to category theory that includes lots of examples, talks to the reader in a friendly way, and explains what’s ‘really going on’. However, while teaching the course, I noticed that Emily Riehl has written a book like this, probably better than I ever could. Even better, her book is free online and will be published by Dover:
• Emily Riehl, Category Theory in Context, 2014.
So, I don’t feel much urge to write that book anymore. But there might still be room for a more quirky book on category theory that only I could write. It would probably need to include not only this ‘standard’ material but more on applications.
If you discover any errors in the notes please email me, and I’ll add them to the list of errors.
You can get all 10 weeks of notes in a single file here:
Or, you can look at individual weeks:
Week 1 (Jan. 5 and 7) – The definition of a category. Some familiar categories. Various kinds of categories, including monoids, groupoids, groups, preorders, equivalence relations and posets. The definition of a functor. Doing mathematics inside a category: isomorphisms, monomorphisms and epimorphisms.
Week 2 (Jan. 12 and 14) – Doing mathematics inside a category: an isomorphism is a monomorphism and epimorphism, but not necessarily conversely. Products. Any object isomorphic to a product can also be a product. Products are unique up to isomorphism. Coproducts. What products and coproducts are like in various familiar categories. General limits and colimits. Examples: products and coproducts, equalizers and coequalizers, pullbacks and pushouts, terminal and initial objects.
Week 3 (Jan. 19 and 21) – Equalizers and coequalizers, and what they look like in 
Week 4 (Jan. 26 and 28) – Doing mathematics between categories. Faithful, full, and essentially surjective functors. Forgetful functors: what it means for a functor to forget nothing, forget properties, forget structure or forget stuff. Transformations between functors. Natural transformations. Functor categories. Natural isomorphisms. In a category with binary products, the product becomes a functor, and the commutative and associative laws hold up to natural isomorphism. Cartesian categories. In a cartesian category, the left and right unit laws also hold up to natural isomorphism. A 
Week 5 (Feb. 2 and 4) – A 
Week 6 (Feb. 9 and 11) – Diagrams in a category as functors. Cones as natural transformations. The process of taking limits as a right adjoint. The process of taking colimits as a left adjoint. Left adjoints preserve colimits; right adjoints preserve limits. Examples: the ‘free group’ functor from sets to groups preserve coproducts, while the forgetful functor from groups to sets preserves products. The composite of left adjoints is a left adjoint; the composite of right adjoints is a right adjoint. The unit and counit of a pair of adjoint functors.
Week 7 (Feb. 16 and 18) – Adjunctions. The naturality of the isomorphism 
Week 8 (Feb. 23) – Internalization. The concept of a group in a cartesian category. Any pair of objects 
Week 8 (Feb. 25) – Guest lecture by Christina Osborne on symmetric monoidal categories.
Week 9 (Mar. 1 and 3) – For any category 
Week 10 (Mar. 8 and 10) – The subobject classifier in the topos of graphs. Any topos has finite colimits. Any morphism in a topos has an epi-mono factorization, which is unique up to a unique isomorphism. The image of a morphism in topos. The poset 
Where does topos theory go from here?
All the notes are handwritten, by Christina Osborne and Samuel Britton. I’d consider paying someone to TeX them up! But as you see, there are a lot of diagrams…. so you should only try it if you want to learn category theory while practicing your TikZ. And if you try it, you should let us know – it would be silly to have more than one person doing the same job, while chopping the job into parts might work well.
Azimuth 
John – do not give up on the idea of an introductory text on category theory. Having read your student’ notes and perused Riehl’s book my judgment is that it needs another ten years of real world experience to be really useful outside of a limited maths fraternity. You could do this now – pulling in engineers, computer scientists and even physicist. Kind regards Jeff Tansley
Yes, my class was aimed at math grad students: the goal was to show that category theory unifies and simplifies a lot of what they already know. A math grad student, when they hear how equalizers in the category of abelian groups are the same as kernels, whereas equalizers but not kernels make sense in the category of sets, should get a happy sensation inside, like “aha, now I see why they always talk about kernels in group theory but not set theory!” A nonmathematician is likely to say “huh?” Of course, a lot of these insights were transmitted in words that didn’t get written on the blackboard, so these notes would need a lot of work to become a book!
A book for engineers, computer scientists and physicists would need to be completely different. David Spivak has written one:
• David Spivak, Category theory for scientists.
If I wrote one, it would be very different: it would include a lot about Feynman diagrams, electrical circuits, Markov processes and chemical reaction networks.
I have downloaded the books by David Spivak (sometime ago when you mentioned it) and Emily Riehl (today). I have skimmed them and I like them. I don’t feel motivated to read them because I don’t see how how they could be useful to me. The book you might write might help with that!
I wouldn’t expect Emily Riehls’ book to be helpful to you: it should be great for anyone with a strong background in modern algebra and topology, but that’s not you.
David Spivak is trying to write for “scientists”, so that book may be intended for people like you (though “scientists” is a very broad audience). I am very interested to hear how various scientists react to his book, because I might someday try a vaguely similar book. I suspect most scientists would want to see more concrete examples drawn from their own field—which would make it challenging to appeal to all of them. Perhaps chapters on different basic concepts, with each chapter containing a section for biologists, a section for chemists, a section for physicists and a section for computer scientists. (That’s about all the fields I can dream of handling, and ‘biology’ is almost too broad to count as one field.)
I was a pure mathematician a long time ago. At least this means I am not frightened by the purely abstract nature of Emily Riehls’ book. David Spivak has applications, but they mostly involve databases. I saw one mention of a Markov chain. My impression is that his applications are almost all about structured information, not processes.
I am not really looking for concrete examples drawn from my own field of evolutionary biology. I can recognise Markov processes and chemical reaction networks as relevant to my work, and electrical circuits and even Feynman diagrams as relevant to others in the field. There are plenty of databases used in evolutionary biology too, but they don’t interest me!
Should it come to pass that you write a vaguely similar book to Spivak’s, perhaps it should have chapters with titles like ‘Structured information’, ‘Transforming information’, ‘Continuous time processes’, or some such.
Hi John
Back in 1975 or 1976 I started Ross Street’s Algebra III course which was a thinly veiled front for category theory! I lasted about two weeks (there it’s out and I feel better!) and then picked up Fourier theory which I loved then and still do (and actually used it when I worked in defence). Since I’ve been retired I have looked at the enthusiastic stuff you have written and I have tried to go back and get my mind into category theory. I must say, at first blush, David Spivak’s book is the closest I have come to a book which joins the dots for me in a meaningful way. I will put some more time into it given that he has obviously devoted an enormous amount of thought to communicating the concepts. If someone could come up with a category theoretical explanation of why the Fourier transform of a gaussian is a gaussian I’d be intrigued. I might even become an acolyte at its altar….
Cheers
Peter
It might help to know there’s a ‘quantization functor’
where
is the category of complex Hilbert spaces and unitary operators. If you apply this functor to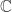 
you get a Hilbert space isomorphic to 
, and if you apply it to the operator of multiplication by 
you get the Fourier transform. This explains why the fourth power of the Fourier transform is the identity. With a bit more work you can show that 
has an orthonormal basis of eigenvectors of the Fourier transform. Applied to the 
th eigenvector, the Fourier transform acts as multiplication by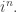 
The 
th vector is the 
th eigenvector of the quantum harmonic oscillator Hamiltonian, so the ground state of the quantum harmonic oscillator, the Gaussian, is its own Fourier transform.
I don’t think you can use just category theory to understand this stuff: that’s not how it works. But category theory provides part of the framework for deeply understanding this stuff: that’s how it works.
John
What you have just done above is an exercise in Eli Stein’s and Rami Shakarchi’s Fourier Series book which drags in Hermite functions as part of the overall proof. No mention of category theory of course. All bare hands stuff. I can see how category theory can illuminate structural things across seemingly disparate areas. I’ll bat on with David’s book to get a bit more proficient with the detail..
Cheers
Peter
You don’t actually need to mention Hermite functions or use a formula for the Hermite functions to prove this result; one can do everything a bit abstractly and just define the
th Hermite function to be the 
th eigenvector of the harmonic oscillator (possibly times normalization factor, if you want to make life more complicated than it strictly needs to be). No grungy formulas or grungy manipulations are required, since this is part of the math gods’ favored territory.
My take on books and authors, if I may:
Given the pervasiveness of programming (languages) in all disciplines, I think writing a book with some bias towards a computer science audience would channel the interest of quite a vast range of backgrounds (math, physics, CS, chemistry, bioinformatics…). Substitute “computer science” by “Haskell” and then it might be clearer what I mean perhaps. I would buy a book on the subject written by you with Dan Piponi and maybe Mike Stay as well. Riehl gives has some examples from Haskell but there could be way many more. I’m thinking an intro level book for people with some solid background in undergrad algebra.
Unfortunately I dislike programming, and I’ve never programmed in Haskell, so I’m not the right person to write a book that connects category theory and computer science. The closest I came is this paper, which you may already know:
• John Baez and Mike Stay, Physics, topology, logic and computation: a Rosetta Stone, in New Structures for Physics, ed. Bob Coecke, Lecture
Notes in Physics vol. 813, Springer, Berlin, 2011, pp. 95–172.
Mike supplied the practical expertise in programming, and I supplied the expertise in symmetric monoidal closed categories, and together we put together a pretty nice section on how they fit together. But this was really just scratching the surface of categories and computation! To really get serious I think one would need to bring in 2-categories, and nobody has fully worked out the details yet. I tried here:
• John Baez, Categories and computation.
See especially the references to Seeley near the end.
I wish someone would work out all the details and write a great book about it, full of pictures!
Is the reason for your interest in category theory a sort of “top-down” thing? In other words the category theory allows you to “sniff” something structural about some aspect of quantum physics, say, but then you have to go down a level and do the grunge work of actually showing that the “sniff” was right. Or is it a situation of if we are all category theory equipped we can see the more abstract reason why something works without descending into the grunge (and what you say above is probably a good example)?
It’s a bit tricky to explain how category theory actually helps. It’s sort of like having an extra pair of eyes that can see patterns that would otherwise be invisible. It’s sort of like knowing an extra language that lets you think thoughts you just couldn’t think otherwise. And it’s sort of like having an overall map of mathematics.
Sometimes category theory makes long and clumsy proofs short and efficient. Sometimes it lets you guess what you should try to prove, but you still have to struggle through some grunge to prove those things. But most of all it lets you state theorems that you just couldn’t state without category theory—at least not without lots of clumsy circumlocutions.
I also find it hard to describe the power of categorical thinking, but one thing that a committedly categorical approach helps to do is to clear away conceptual clutter and distill mathematical situations down to their essences. One aphorism for this is due to Peter Freyd: “Perhaps the purpose of categorical algebra is to show that which is trivial is trivially trivial.” This sounds like he’s making a little joke, but he has a serious point: that one thing category theory does is help make the softer bits seem utterly natural and obvious, so as to quickly get to the heart of the matter, allowing one to isolate the hard nuggets, which one may then attack with abandon. (I’m paraphrasing the nLab, but that’s okay since I wrote the relevant passage.)
One of the great exemplars and high artists of the categorical spirit was Alexandre Grothendieck, who had a way of dissolving problems, not by attacking them head-on — what he called the hammer and chisel approach — but by soaking them within a vast sea of theory. This is even more mysterious than Freyd’s dictum, and very hard to describe, but the style consists much more in finding the right kinds of definitions, lifting problems to a higher plane where former obstacles become spurious, are swept away. Few mathematicians can really pull this off, but in the end a thoroughgoingly Grothendieckian approach will also give an impression of utter naturality — what John Baez fondly calls the ‘Tao’ of mathematics. Pierre Deligne said this: “a typical Grothendieck proof consists of a long series of trivial steps where “nothing seems to happen, and yet at the end a highly non-trivial theorem is there”.
Nice comments, Todd!
Some links to learning resources:
‘Category Theory for the Sciences’ by David I. Spivak (via Source)
‘Category Theory for Scientists’ by David I. Spivak (via Source, see comments from John Baez)
‘Category theory in context’ by Emily Riehl (via Source < via Source)