There’s a new paper on the arXiv that claims to solve a hard problem:
• Norbert Blum, A solution of the P versus NP problem.
Most papers that claim to solve hard math problems are wrong: that’s why these problems are considered hard. But these papers can still be fun to look at, at least if they’re not obviously wrong. It’s fun to hope that maybe today humanity has found another beautiful grain of truth.
I’m not an expert on the P versus NP problem, so I have no opinion on this paper. So don’t get excited: wait calmly by your radio until you hear from someone who actually works on this stuff.
I found the first paragraph interesting, though. Here it is, together with some highly non-expert commentary. Beware: everything I say could be wrong!
Understanding the power of negations is one of the most challenging problems in complexity theory. With respect to monotone Boolean functions, Razborov [12] was the first who could shown that the gain, if using negations, can be super-polynomial in comparision to monotone Boolean networks. Tardos [16] has improved this to exponential.
I guess a ‘Boolean network’ is like a machine where you feed in a string of bits and it computes new bits using the logical operations ‘and’, ‘or’ and ‘not’. If you leave out ‘not’ the Boolean network is monotone, since then making more inputs equal to 1, or ‘true’, is bound to make more of the output bits 1 as well. Blum is saying that including ‘not’ makes some computations vastly more efficient… but that this stuff is hard to understand.
For the characteristic function of an NP-complete problem like the clique function, it is widely believed that negations cannot help enough to improve the Boolean complexity from exponential to polynomial.
A bunch of nodes in a graph are a clique if each of these nodes is connected by an edge to every other. Determining whether a graph with 
For example, here’s a brute-force search for a clique with at least 4 nodes:
The clique decision problem is NP-complete. This means that if you can solve it with a Boolean network whose complexity grows like some polynomial in n, then P = NP. But if you can’t, then P ≠ NP.
(Don’t ask me what the complexity of a Boolean network is; I can guess but I could get it wrong.)
I guess Blum is hinting that the best monotone Boolean network for solving the clique decision problem has a complexity that’s exponential in 
Since the computation of an one-tape Turing machine can be simulated by a non-monotone Boolean network of size at most the square of the number of steps [15, Ch. 3.9], a superpolynomial lower bound for the non-monotone network complexity of such a function would imply P ≠ NP.
Now he’s saying what I said earlier: if you show it’s impossible to solve the clique decision problem with any Boolean network whose complexity grows like some polynomial in n, then you’ve shown P ≠ NP. This is how Blum intends to prove P ≠ NP.
For the monotone complexity of such a function, exponential lower bounds are known [11, 3, 1, 10, 6, 8, 4, 2, 7].
Should you trust someone who claims they’ve proved P ≠ NP, but can’t manage to get their references listed in increasing order?
But until now, no one could prove a non-linear lower bound for the nonmonotone complexity of any Boolean function in NP.
That’s a great example of how helpless we are: we’ve got all these problems whose complexity should grow faster than any polynomial, and we can’t even prove their complexity grows faster than linear. Sad!
An obvious attempt to get a super-polynomial lower bound for the non-monotone complexity of the clique function could be the extension of the method which has led to the proof of an exponential lower bound of its monotone complexity. This is the so-called “method of approximation” developed by Razborov [11].
I don’t know about this. All I know is that Razborov and Rudich proved a whole bunch of strategies for proving P ≠ NP can’t possibly work. These strategies are called ‘natural proofs’. Here are some friendly blog articles on their result:
• Timothy Gowers, How not to prove that P is not equal to NP, 3 October 2013.
• Timothy Gowers, Razborov and Rudich’s natural proofs argument, 7 October 2013.
From these I get the impression that what Blum calls ‘Boolean networks’ may be what other people call ‘Boolean circuits’. But I could be wrong!
Continuing:
Razborov [13] has shown that his approximation method cannot be used to prove better than quadratic lower bounds for the non-monotone complexity of a Boolean function.
So, this method is unable to prove some NP problem can’t be solved in polynomial time and thus prove P ≠ NP. Bummer!
But Razborov uses a very strong distance measure in his proof for the inability of the approximation method. As elaborated in [5], one can use the approximation method with a weaker distance measure to prove a super-polynomial lower bound for the non-monotone complexity of a Boolean function.
This reference [5] is to another paper by Blum. And in the end, he claims to use similar methods to prove that the complexity of any Boolean network that solves the clique decision problem must grow faster than a polynomial.
So, if you’re trying to check his proof that P ≠ NP, you should probably start by checking that other paper!
The picture below, by Behnam Esfahbod on Wikicommons, shows the two possible scenarios. The one at left is the one Norbert Blum claims to have shown we’re in.
Azimuth 
I found at least one error in your commentary: you defined the “circuit complexity” of a boolean network, not the “algorithmic complexity”, but P != NP is about algorithmic complexity. (The circuit complexity is when you let the network be constructed arbitrarily as a function of the number of inputs
; the algorithmic complexity is when the network has to follow some pattern that would let a Turing machine construct it “reasonably fast” (I’ll defer to experts for a precise definition of “fast”).)
So the equivalence you state is only an implication, since algorithmic complexity is greater than or equal to circuit complexity. In other words, being able to get the optimal circuit (for a given number of inputs) “from God”, rather than having to construct it using a fixed algorithm independent of
, can (sometimes) give you an advantage in its size.
(I haven’t yet read the rest of your post. I haven’t yet noticed an error in the paper itself (but haven’t looked very hard, or beyond its page 10).)
After reading your next paragraph, I take it back — you don’t claim to have defined the “complexity of a Boolean network”, therefore you haven’t been specific enough to make the error I claimed. Normally that complexity is just defined as the number of nodes in the network (sometimes not counting NOT gates, but that doesn’t matter if you’re only worried about “polynomial time or not”) — I had just assumed you meant that definition when I made my prior remark.
But maybe it’s still worth being more specific about your not-quite-error: using “number of nodes in the network” for “complexity”, this statement is not correct:
The reason is that it’s possible in principle that you can solve it with a small network like that, but there is no fast-enough algorithm for constructing that network (given
), so an algorithm to solve the same problem might still have to be superpolynomial time in 
.
If Blum is correct, then, he has proved something significantly stronger than P != NP (though it’s a well-known target for people interested in trying to prove that).
Bruce wrote:
Good! I don’t remember doing anything like defining this. In fact I wrote:
I finished your post. (Yes, ‘boolean network’ is just another name for ‘boolean circuit’.)
Note that Blum does claim (on page 4 of his paper) that his proof method is not ruled out by the “natural proofs” limitation, due to the fact that his method can (in principle) only be applied to monotone functions (even though it can be applied to non-monotone circuits used to compute those functions).
It looks to me as though the paper gets a very low crackpot-index score (where high => crackpot). Of course, that doesn’t mean that it is correct, but I think it may reach the level where the experts feel that it needs to be checked.
For what it’s worth, the author is a chair of the computer science department at the University of Bonn, and reference [5], the paper the current one relies on, was published in a somewhat reputable place:
• Norbert Blum, On negations in Boolean networks, in Efficient Algorithms: Essays Dedicated to Kurt Mehlhorn on the Occasion of His 60th Birthday, Lecture Notes in Computer Science 5760 (2009), Springer, Berlin, pp. 18–29.
On G+, Boyd Smith wrote:
Unfortunately this earlier paper is not open-access. Springer will sell it to you for €24.95. (That sounds so much more tempting than €25!)
Surely, €24.95 is a small price to pay for invaluable insights into one of humanities greatest mysteries?!
Sally will let you have a look for 10 quids. (OP can have a looksie for 9.95)
I’m also pretty sure that “open access” means nothing in the age of Sci Hub. One can always find a copy of a paper one wants to read.
Clearly a task for Sci-Hub!
The order of the references is increasing by year of publication.
Okay, good! That’s reassuring.
Leaving us with yet another pressing question: Should you trust a blog author who can’t figure out that a reference list is sorted by publication year?
You mean: can you trust a blog author who didn’t really care enough about this issue to figure it out?
I was waiting calmly by my radio, and heard instead that Michael Atiyah has a 12-page proof of Feit and Thompson’s odd order theorem. A 5-minute interview begins at about 2:49:00 here: http://www.bbc.co.uk/programmes/b090vd75. I can’t find a paper.
Interesting! I would be suspicious of this, because experts believe his last claimed breakthrough paper, called The non-existent complex 6-sphere, is wrong. I believe the days of his mathematical peak performance are gone, and people in the know are aware of this, but too tactful to point this out publicly.
and you must have about as much tact as scott aaronson …..
I’ve never been accused of tact… though if I started saying more of what I thought, people would realize in retrospect how tactful I had really been.
[…] Si quieres la opinión de otro inexperto en complejidad computacional, puedes leer a John Carlos Baez, “Norbert Blum on P versus NP,” Azimuth, 15 Aug 2017. […]
I haven’t seen any big name in the field dismiss this paper, so chances are good that it’s sound. Also, there’s glory and money on the line for such a publication ($1M if not mistaken with glory being a sufficient motivator); the author probably was in a hurry to get it out being excited about it (I also suspect he believed long ago he could solve it, hence he worked patiently alone without collaborators as he didn’t find that necessary). The last thing that was on his mind is minor language typos (there are some) and precise ordering of references. Note that the list of references is rather short for an academic paper; I interpret that to mean “only what I really needed to get this done will be referenced”.
I am not from this field but came close to joining in (Ph.D. drop out from U. of Toronto 30 years ago, where Cook worked and Razborov and Rudich came to visit) and have no understanding of the technical arguments presented.
Thanks! By the way, my remark about the ordering of references was a joke: I don’t really care much about the ordering of references, and I would never use that as a way to judge the mathematical content of a paper.
I’m confused by the following point in the paper:
On p. 27 there is a description of a DNF’ representation of a standard network (De Morgan circuit).
On p. 29 Thm. 5, it is claimed that if C is standard network computing a monotone function f, then all monomials contained in DNF'(C) are
implicants of f.
I fail to see this. For example, let f be the monotone function computed by the circuit C = (x or y) and (not x or y) and (x or not y).
If I’ve understood the construction correctly, DNF'(C) = x or y or xy, but obviously neither x nor y is an implicant of f.
To add to this, I don’t see why, from the first two paragraphs of the proof of Theorem 5, we can conclude that DNF'(g_0) computes f. I see only some sort of one-sided-ness that DNF'(g_0) computes a function such that f = 1 implies that this function is also 1.
The third paragraph doesn’t help me either: surely DNF'(g_0) and its DNF/CNF-switch compute the same function, but it does not immediately follow that the DNF/CNF-switch computes f (because DNF'(g_0) might not), so we can’t make any conclusions about f-clauses.
(Aside: this one-sided-ness is consistent with Gustav’s example above.)
From a different viewpoint, surely a standard network computing a monotone function could compute non-monotone functions at internal nodes. Theorem 5 doesn’t apply to non-monotone functions, so DNF'(g) might not correctly compute the sub-function in the network whose output node is g (which will happen for many non-monotone functions). Because of this, I’m not convinced that this inductive construction of DNF'(g_0) will necessarily be correct in the end.
If I’m totally off-base here, please let me know!
Others have picked up on this comment: see here and here.
[…] Baez has very quickly put together a post explaining the very basics of Blum’s argument. Even more briefly, Blum claims to have shown that the best-case complexity of a function solving […]
This is one of those Millennium Problems, right?
http://www.claymath.org/millennium-problems/p-vs-np-problem
Just blogged a post this morning on another Millennium Problem – this regarding Navier-Stokes:
http://contextearth.com/2017/08/15/millenium-prize-problem-navier-stokes/
The key is to constrain the premise and then solve an applied science problem
Scott Aaronson makes an argument on his latest blog post that this proof is most probably wrong.
Thanks for pointing that out. Here is Aaronson’s argument:
Over on Facebook, Luca Trevisan wrote:
Alas, I have no understanding of this issue.
Luca seems to have retracted this particular counterargument in the comment section of the FB post.
Yes, Luca Trevisan wrote:
Scott Aaronson has removed his mention of Luca Trevisan’s objection from his blog.
Thanks for this.
Further discussions are at https://cstheory.stackexchange.com/questions/38803/where-is-norbert-blums-2017-proof-that-p-ne-np-being-discussed . They are currently a better typesetted version of the comments here, but that might still be useful.
If anyone is looking for “realtime” informed discussion of this paper — the main place I can find is the stackexchange post referenced by Todd Trimble above: https://cstheory.stackexchange.com/questions/38803 .
There is also an older opinion on Quora at https://www.quora.com/Whats-the-status-of-Norbert-Blums-claim-that-operatorname-P-neq-operatorname-NP , and a discussion at http://motls.blogspot.com/2017/08/a-future-proof-of-pnp-or-pnp-may-be-far.html . These are a few hours less up to date, but might continue to receive new comments.
Does anyone know of other places?
The correctness of the claimed proof is being discussed at Luca Trevisan’s blog: https://lucatrevisan.wordpress.com/2017/08/15/on-norbert-blums-claimed-proof-that-p-does-not-equal-np/
In particular “anon” posted the following relevant comment:
“Tardos observed that Razborov’s and Alon-Boppana’s arguments carry over to a function which is computed by a polynomial size non-monotone circuit (the function is a small variant on approximating the Lovasz theta function of the graph). If Berg and Ulfberg’s arguments also apply for Tardos’ function (which is intuitively likely, as their proof seems to be based on Razborov’s proof) then it is clear that that Blum’s current claim cannot be correct. Unfortunately, the author does not discuss this point.”
Thanks, Gustav! Luca Trevisan’s blog entry is very much worth reading.
Yes, that blog entry is an extremely clear summary of how the claimed proof builds on and relates to other results, and of some ways it can be checked for possible flaws (aside from just checking it intrinsically).
This newer blog post (by well-known complexity theorists) is well worth reading, even now that the Blum proof appears to have been invalidated: https://rjlipton.wordpress.com/2017/08/17/on-the-edge-of-eclipses-and-pnp/
I would like to point out that one of Norbert Blum’s co-workers in Bonn, Mathias Hauptmann, has published a preprint on the arxiv that separates P from a class in the polynomial hierarchy. In other words, the polynomial hierarchy does not collapse.
• Mathias Hauptmann, On alternation and the union theorem.
I can by no means judge this proof. But since Norbert Blum’s proof raises so much scrutiny, his co-worker Hauptmann’s proof is probably now of broader interest to you.
Wow, I would never have understood the (potential) importance of this paper from its abstract! Thanks!
Yes, the abstract clearly implies PH does not collapse and P!=PSPACE, which is a spectacular result in its own right if correct. So that paper’s getting no attention and hasn’t been submitted for publication is a sign that it hasn’t stood up to scrutiny. It’s been up since Feb 2016 or so.
Err…doesn’t Hauptmann’s purported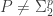
imply 
?
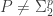, then 
(as 
).
, then 
(see book of Arora & Barak, Theorem 5.4, 2., use contraposition).
If
If
strangely Hauptmann and Blum are at the same university. here was some reaction to Hauptmanns proof which experts didnt take seriously at the time, and still feel it needs/ deserves more attn from experts (over a year later). in contrast Blums proof has gone viral at this point. a bit amused/ delighted, my hits for this old Hauptmann claim are burning up lately. a lot from Germany :)
https://vzn1.wordpress.com/2016/06/20/hauptmann-p%e2%89%a0np-attack-via-polynomial-hierarchy-noncollapse/
Blum’s attack is in a very nice area of complexity theory, circuit complexity theory, that i have been studying for over a decade, and have written in my blog years ago that it may be one of the most viable attack directions on P vs NP. would like to see a collaborative attack in this area, polymath style. in any case the review of this Blum proof is already a natural polymath-oriented effort. if only it could be sustained/built on further as world experts on this topic coalesce/huddle. great to see cyberteamwork in action at times. <3 :) :cool: :star:
am planning to blog on this soon, a bit overwhelmed this moment/morning though.
ps hi gowers! small world! :) :P
[…] Normbert Blum argumenta que la mejor red booleana monotona para resolver el problema del clique está acotada exponenancialmente por abajo y que ese límite también aplica a las redes no monótonas. Eso implicaría que P≠NP según el. Ya han salido diversos científicos cuestionando su forma de demostrar el problema, como John Baez. […]
[…] are following an ongoing discussion on StackExchange and in comments to a post by Luca Trevisan, a post by John Baez, and a Hacker News thread, among several other […]
[…] 2. Norbert Blum on P versus NP | Azimuth […]
Tardos’ example seems to refute the proof.
here is the link for the paper
Click to access Gap.Between.Monotone.NonMonotone.Circuit.Complexity.is.Exponential.pdf
There is some commentary on this at the CS Theory Stackexchange thread, here and here. So there is growing consensus that the proof is cooked; if so, this confirms Scott Aaronson’s prediction that the purported proof would be refuted by the end of the week.
It is now very clear that the proof is wrong. See https://cstheory.stackexchange.com/a/38836 for an exposition on the fatal error which was exposed.
Thanks! Yes, Razborov is a god of complexity theory, so this report by Mikhail if true is enough for me:
Idolvon’s remark pointing out in detail “the single error” is also worth reading, though I’m not technically qualified to evaluate it.
vloodin wrote:
By the way, there’s now a Wikipedia article on this graph invariant introduced by Éva Tardos in 1988:
• Wikipedia, Tardos function.
[…] John Baez’ Blog […]
[…] J. Baez. Blog post from 2017/08/15 and ongoing […]
[…] been covered at length elsewhere: see especially Luca’s post, Dick Lipton’s post, John Baez’s post, and the CS Theory StackExchange […]
This comment on Scott Aaronson’s blog says that Norbert Blum has retracted his claim: https://www.scottaaronson.com/blog/?p=3409#comment-1743815
Yes, Norbert Blum has added this comment on the arXiv:
So this story is done… for now! I hope everyone trying to prove P = NP is now aware of the Tardos function, the example which could have let Norbert Blum know his proof could not possibly work. There’s now a Wikipedia entry on it:
• Wikipeda, Tardos function.
On G+, Timothy Gowers wrote:
https://arxiv.org/abs/1711.10874
can some one comment on this?
More here.