guest post by Christian Williams
Mike Stay has been doing some really cool stuff since earning his doctorate. He’s been collaborating with Greg Meredith, who studied the π-calculus with Abramsky, and then conducted impactful research and design in the software industry before some big ideas led him into the new frontier of decentralization. They and a great team are developing RChain, a distributed computing infrastructure based on the reflective higher-order π-calculus, the ρ-calculus.
They’ve made significant progress in the first year, and on April 17-18 they held the RChain Developer Conference in Boulder, Colorado. Just five months ago, the first conference was a handful of people; now this received well over a hundred. Programmers, venture capitalists, blockchain enthusiasts, experts in software, finance, and mathematics: myriad perspectives from around the globe came to join in the dawn of a new internet. Let’s just say, it’s a lot to take in. This project is the real deal – the idea is revolutionary, the language is powerful, the architecture is elegant; the ambition is immense and skilled developers are actually bringing it to reality. There’s no need for hype: you’re gonna be hearing about RChain.
Documentation , GitHub , Architecture
Here’s something from the documentation:
The open-source RChain project is building a decentralized, economic, censorship-resistant, public compute infrastructure and blockchain. It will host and execute programs popularly referred to as “smart contracts”. It will be trustworthy, scalable, concurrent, with proof-of-stake consensus and content delivery.
The decentralization movement is ambitious and will provide awesome opportunities for new social and economic interactions. Decentralization also provides a counterbalance to abuses and corruption that occasionally occur in large organizations where power is concentrated. Decentralization supports self-determination and the rights of individuals to self-organize. Of course, the realities of a more decentralized world will also have its challenges and issues, such as how the needs of international law, public good, and compassion will be honored.
We admire the awesome innovations of Bitcoin, Ethereum, and other platforms that have dramatically advanced the state of decentralized systems and ushered in this new age of cryptocurrency and smart contracts. However, we also see symptoms that those projects did not use the best engineering and formal models for scaling and correctness in order to support mission-critical solutions. The ongoing debates about scaling and reliability are symptomatic of foundational architectural issues. For example, is it a scalable design to insist on an explicit serialized processing order for all of a blockchain’s transactions conducted on planet earth?
To become a blockchain solution with industrial-scale utility, RChain must provide content delivery at the scale of Facebook and support transactions at the speed of Visa. After due diligence on the current state of many blockchain projects, after deep collaboration with other blockchain developers, and after understanding their respective roadmaps, we concluded that the current and near-term blockchain architectures cannot meet these requirements. In mid-2016, we resolved to build a better blockchain architecture.
Together with the blockchain industry, we are still at the dawn of this decentralized movement. Now is the time to lay down a solid architectural foundation. The journey ahead for those who share this ambitious vision is as challenging as it is worthwhile, and this document summarizes that vision and how we seek to accomplish it.
We began by admitting the following minimal requirements:
- Dynamic, responsive, and provably correct smart contracts.
- Concurrent execution of independent smart contracts.
- Data separation to reduce unnecessary data replication of otherwise independent tokens and smart contracts.
- Dynamic and responsive node-to-node communication.
- Computationally non-intensive consensus/validation protocol.
Building quality software is challenging. It is easier to build “clever” software; however, the resulting software is often of poor quality, riddled with bugs, difficult to maintain, and difficult to evolve. Inheriting and working on such software can be hellish for development teams, not to mention their customers. When building an open-source system to support a mission-critical economy, we reject a minimal-success mindset in favor of end-to-end correctness.
To accomplish the requirements above, our design approach is committed to:
- A computational model that assumes fine-grained concurrency and dynamic network topology.
- A composable and dynamic resource addressing scheme.
- The functional programming paradigm, as it more naturally accommodates distributed and parallel processing.
- Formally verified, correct-by-construction protocols which leverage model checking and theorem proving.
- The principles of intension and compositionality.
RChain is light years ahead of the industry. Why? It is upholding the principle of correct by construction with the depth and rigor of mathematics. For years, Mike and Greg have been developing original ideas for distributed computation: in particular, logic as a distributive law is an “algorithm for deriving a spatial-behavioral type system from a formal presentation of a computational calculus.” This is a powerful way to integrate operational semantics into a language, and prove soundness with a single natural transformation; it also provides an extremely expressive query language, with which you could search the entire world to find “code that does x”. Mike’s strong background in higher category theory has enabled the formalization of Greg’s ideas, which he has developed over decades of thinking deeply and comprehensively about the world of computing. Of all of these, there is one concept which is the heart and pulse of RChain, which unifies the system as a rational whole: the ρ-calculus.
So what’s the big idea? First, some history: back in the late 80s, Greg developed a classification of computational models called “the 4 C’s”:
completeness,
compositionality,
(a good notion of) complexity, and
concurrency.
He found that there was none which had all four, and predicted the existence of one. Just a few years later, Milner invented the π-calculus, and since then it has reigned as the natural language of network computing. It presents a totally different way of thinking: instead of representing sequential instructions for a single machine, the π-calculus is fundamentally concurrent—processes or agents communicate over names or channels, and computation occurs through the interaction of processes. The language is simple yet remarkably powerful; it is deeply connected with game semantics and linear logic, and has become an essential tool in systems engineering and biocomputing: see mobile process calculi for programming the blockchain.
Here is the basic syntax. The variables x,y are names, and P,Q are processes:
P,Q := 0 | (νx)P | x?(y).P | x!(y).P | P|Q
(do nothing | create new x; run P | receive on x and bind to y; run P | send value y on x; run P | run P and Q in parallel)
The computational engine, the basic reduction analogous to beta-reduction of lambda calculus, is the communication rule:
COMM : x!(y).P|x?(z).Q → P|Q[y/z]
(given parallel output and input processes along the same channel, the value is transferred from the output to the input, and is substituted for all occurrences of the input variable in the continuation process)
The definition of a process calculus must specify structural congruence: these express the equivalences between processes—for example, ({P},|,0) forms a commutative monoid.
The π-calculus reforms computation, on the most basic level, to be a cooperative activity. Why is this important? To have a permanently free internet, we have to be able to support it without reliance on centralized powers. This is one of the simplest points, but there are many deeper reasons which I am not yet knowledgeable enough to express. It’s all about the philosophy of openness which is characteristic of applied category theory: historically, we have developed theories and practices which are isolated from each other and the world, and had to fabricate their interrelation and cooperation ad hoc; this leaves us needlessly struggling with inadequate systems, and limits our thought and action.
Surely there must be a less primitive way of making big changes in the store than by pushing vast numbers of words back and forth through the von Neumann bottleneck. Not only is this tube a literal bottleneck for the data traffic of a problem, but, more importantly, it is an intellectual bottleneck that has kept us tied to word-at-a-time thinking instead of encouraging us to think in terms of the larger conceptual units of the task at hand. Thus programming is basically planning and detailing the enormous traffic of words through the von Neumann bottleneck, and much of that traffic concerns not significant data itself, but where to find it. — John Backus, 1977 ACM Turing Award
There have been various mitigations to these kind of problems, but the cognitive limitation remains, and a total renewal is necessary; the π-calculus completely reimagines the nature of computation in society, and opens vast possibility. We can begin to conceive of the many interwoven strata of computation as a coherent, fluid whole. While I was out of my depth in many talks during the conference, I began to appreciate that this was a truly comprehensive innovation: RChain reforms almost every aspect of computing, from the highest abstraction all the way down to the metal. Coalescing the architecture, as mentioned earlier, is the formal calculus as the core guiding principle. There was some concern that because the ρ-calculus is so different from traditional languages, there may be resistance to adoption; but our era is a paradigm shift, the call is for a new way of thinking, and we must adapt.
So why are we using the reflective higher-order π-calculus, the ρ-calculus? Because there’s just one problem with the conventional π-calculus: it presupposes a countably infinite collection of atomic names. These are not only problematic to generate and manage, but the absence of structure is a massive waste. In this regard, the π-calculus was incomplete, until Greg realized that you can “close the loop” with reflection, a powerful form of self-reference:
Code ←→ Data
The mantra is that names are quoted processes; this idea pervades and guides the design of RChain. There is no need to import infinitely many opaque, meaningless symbols—the code itself is nothing but clear, meaningful syntax. If there is an intrinsic method of reference and dereference, or “quoting and unquoting”, code can be turned into data, sent as a message, and then turned back into code; known as “code mobility”, one can communicate big programs as easily as emails. This allows for metaprogramming: on an industrial level, not only people write programs—programs write programs. This is essential to creating a robust virtual infrastructure.
So, how can the π-calculus be made reflective? By solving for the least fixed point of a recursive equation, which parametrizes processes by names:
P[x] = 0 | x?(x).P[x] | x!(P[x]) | P[x]|P[x] | @P[x] | *x
RP = P[RP]
This is reminiscent of how the Y combinator enables recursion by giving the fixed point of any function, Yf = f(Yf). The last two terms of the syntax are reference and dereference, which turn code into data and data into code. Notice that we did not include a continuation for output: the ρ-calculus is asynchronous, meaning that the sender does not get confirmation that the message has been received; this is important for efficient parallel computation and corresponds to polarised linear logic. We adopt the convention that names are output and processes are input. The last two modifications to complete the official ρ-calculus syntax are multi-input and pattern-matching:
P,Q := 0 null process
| for(p1←x1,…,pn←xn).P input guarded process
| x!(@Q) output a name
| *x dereference, evaluate code
| P|Q parallel composition
x,p := @P name or quoted process
(each ‘pi’ is a “pattern” or formula to collect terms on channel ‘xi’—this is extremely useful and general, and enables powerful functionality throughout the system)
Simple. Of course, this is not really a programming language yet, though it is more usable than the pure λ-calculus. Rholang, the actual language of RChain, adds some essential features:
ρ-calculus + variables + useful ground terms + new name construction + arithmetic + pattern matching = Rholang
Here’s the specification, syntax and semantics, and a visualization; explore code and examples in GitHub and learn the contract design in the documentation—you can even try coding on rchain.cloud! For those who don’t like clicking all these links, let’s see just one concrete example of a contract, the basic program in Rholang: a process with persistent state, associated code, and associated addresses. This is a Cell, which stores a value until it is accessed or updated:
contract Cell( get, set, state ) = {
select {
case rtn <- get; v <- state => {
rtn!( *v ) | state!( *v ) | Cell( get, set, state ) }
case newValue <- set; v <- state => {
state!( *newValue ) | Cell( get, set, state ) }
}}
The parameters are the channels on which the contract communicates. Cell selects from two possibilities: either it is being accessed, i.e. there is data (the return channel) to receive on get, then it outputs on rtn and maintains its state and call; or it is being updated, i.e. there is data (the new value) to receive on set, then it updates state and calls itself again. This shows how the ontology of the language enables natural recursion, and thereby persistent storage: state is Cell’s way of “talking to itself”—since the sequential aspect of Rholang is functional, one “cycles” data to persist. The storage layer uses a similar idea; the semantics may be related to traced monoidal categories.
Curiously, the categorical semantics of the ρ-calculus has proven elusive. There is the general ideology that λ:sequential :: π:concurrent, that the latter is truly fundamental, but the Curry-Howard-Lambek isomorphism has not yet been generalized canonically—though there has been partial success, involving functor-category denotational semantics, linear logic, and session types. Despite its great power and universality, the ρ-calculus remains a bit of a mystery in mathematics: this fact should intrigue anyone who cares about logic, types, and categories as the foundations of abstract thought.
Now, the actual system—the architecture consists of five interwoven layers (all better explained in the documentation):
Storage: based on Special K – “a pattern language for the web.” This layer stores both key-value pairs and continuations through an essential duality of database and query—if you don’t find what you’re looking for, leave what you would have done in its place, and when it arrives, the process will continue. Greg characterizes this idea as the computational equivalent of the law of excluded middle.
[channel, pattern, data, continuation]
RChain has a refined, multidimensional view of resources – compute, memory, storage, and network—and accounts for their production and consumption linearly.
Execution: a Rho Virtual Machine instance is a context for ρ-calculus reduction of storage elements. The entire state of the blockchain is one big Rholang term, which is updated by a transaction: a receive invokes a process which changes key values, and the difference must be verified by consensus. Keys permanently maintain the entire history of state transitions. While currently based on the Java VM, it will be natively hosted.
Namespace: a set of channels, i.e. resources, organized by a logic for access and authority. The primary significance is scalability – a user does not need to deal with the whole chain, only pertinent namespaces. ‘A namespace definition may control the interactions that occur in the space, for example, by specifying: accepted addresses, namespaces, or behavioral types; maximum or minimum data size; or input-output structure.’ These handle nondeterminism of the two basic “race conditions”, contention for resources:
x!(@Q1) | for(ptrn <- x){P} | x!(@Q2)
for(ptrn <- x){P1} | x!(@Q) | for(ptrn <- x){P2}
Contrasted with flat public keys of other blockchains, domains work with DNS and extend them by a compositional tree structure. Each node as a named channel is itself a namespace, and hence definitions can be built up inductively, with precise control.
Consensus: verify partial orders of changes to the one-big-Rholang-term state; the block structure should persist as a directed acyclic graph. The algorithm is Proof of Stake – the capacity to validate in a namespace is tied to the “stake” one holds in it. Greg explains via tangles, and how the complex CASPER protocol works naturally with RChain.
Contracts: ‘An RChain contract is a well-specified, well-behaved, and formally verified program that interacts with other such programs.’ (K Framework) ; (DAO attack) ‘A behavioral type is a property of an object that binds it to a discrete range of action patterns. Behavioral types constrain not only the structure of input and output, but the permitted order of inputs and outputs among communicating and (possibly) concurrent processes under varying conditions… The Rholang behavioral type system will iteratively decorate terms with modal logical operators, which are propositions about the behavior of those terms. Ultimately properties [such as] data information flow, resource access, will be concretized in a type system that can be checked at compile-time. The behavioral type systems Rholang will support make it possible to evaluate collections of contracts against how their code is shaped and how it behaves. As such, Rholang contracts elevate semantics to a type-level vantage point, where we are able to scope how entire protocols can safely interface.’ (LADL)
So what can you build on RChain? Anything.
Decentralized applications: identity, reputation, tokens, timestamping, financial services, content delivery, exchanges, social networks, marketplaces, (decentralized autonomous) organizations, games, oracles, (Ethereum dApps), … new forms of code yet to be imagined. It’s much more than a better internet: RChain is a potential abstract foundation for a rational global society. The system is a minimalist framework of universally principled design; it is a canvas with which we can begin to explore how the world should really work. If we are open and thoughtful, if we care enough, we can learn to do things right.
The project is remarkably unknown for its magnitude, and building widespread adoption may be one of RChain’s greatest challenges. Granted, it is new; but education will not be easy. It’s too big a reformation for a public mindset which thinks of (technological) progress as incrementally better specs or added features; this is conceptual progression, an alien notion to many. That’s why the small but growing community is vital. This article is nothing; I’m clearly unqualified—click links, read papers, watch videos. The scale of ambition, the depth of insight, the lucidity of design, the unity of theory and practice—it’s something to behold. And it’s real. Mercury will be complete in December. It’s happening, right now, and you can be a part of it. Learn, spread the word. Get involved; join the discussion or even the development—the RChain website has all the resources you need.
40% of the world population lives within 100km of the ocean. Greg pointed out that if we can’t even handle today’s refugee crises, what will possibly happen when the waters rise? At the very least, we desperately need better large-scale coordination systems. Will we make it to the next millennium? We can—just a matter of will.
Thank you for reading. You are great.





Maybe I am too critical, but it would greatly help in spreading a new concept to much more people than the usual few, if mathematicians and even more computer scientists could stop to invent a clutter of new language on the way. Of course one could blame it to the revolutionary character, but these things relate that less to known concepts and are such full of technobabble that it is a constant pain from the beginning to delve inside the topic. Why is that? Is there really no better way for people focussing on technology of communication to communicate with their fellow human beings?
New ideas require new language. Functors, quarks, probability distributions, integrals, addition… we need these words because they describe things for which there weren’t words before. None of these words makes sense until you learn the new ideas they describe. It takes real work.
Nonetheless, I think it’s important to struggle to explain things clearly, at least if they’re important enough to be worth explaining. This also takes real work.
As part of this, one must struggle to minimize the number of new words one uses in any communication, and clearly explain each one. Very few scientists and mathematicians do that. They are generally uninterested in the challenges of clear communication.
Of course, what’s a “new word” depends on one’s audience. But it’s important to remember that choosing to use a large vocabulary means choosing to communicate to a small audience. If one freely uses all the terminology one knows, one winds up talking to oneself.
Yes, agreed. Thanks for your concerns, Wolfgang. Clear communication is absolutely essential for new ideas to be effective. Like I said, I’m unqualified to explain all this, and the article is mainly just a repository for links.
There are many people in the small but growing RChain community who are working together to learn all this new stuff. If you are interested, please ask on any of the online discussions, such as Discord.
Right now, it’s mainly just the core people who have a comprehensive idea of RChain; and not for any kind of elitism or laziness – it’s just a lot of big concepts coming together in practice for the first time.
The public doesn’t know the huge conceptual progress made in the past century, but the biggest innovations will be based on the biggest ideas. It is difficult to close this widening gap, and the only long-term solution is better education.
Until then, we have public educators like Dr. Baez – someone involved in the highest abstractions, yet thoroughly opposed to technobabble, and only focused on helping us all learn together. I hope you’ve gained from reading his blog, as so many have.
You tout rchain’s complexity model. Is it documented somewhere?
The connection to traced monoidal categories is interesting. Is more information available?
About ρ-lang’s fixpoint and its semantics. Would it be convenient to think about it as a guarded fixpoint (https://doi.org/10.2168/LMCS-8(4:1)2012) ? Guarded recursion via the topos of trees gives a convenient model to do synthetic domain theory.
Great questions. The traced monoidal was linked in the documentation to a paper called “Recursion from Cyclic Sharing”, so I assume that this is their theoretical basis.
As for the complexity, I will ask Greg or Mike; as far as I can see it is not in the main documentation, but it is probably somewhere on the GitHub.
Regarding the fixed point, I’m not exactly sure what “guarded” recursion is, but it seems relevant. Above, RP is the solution to the domain equation defined by the rho calculus grammar. Another question for Mike or Greg – they read the blog sometimes, so I’m sure they’ll be a big help for these comments. Thank you!
Nice sign off. I’d like to better understand the semantics of, say the pi-calculus to start. Quick context: when I’m teaching students how to compose functions, I like to use an analogy with composing the process of putting on socks with the process of putting on shoes. It’s nice because it highlights how commutativity fails. Can you think of an analogy in a similar spirit to explain your favorite term of the pi-calculus? I think it’d be helpful.
This would be very good—perhaps a step toward a categorical semantics of the pi-calculus!
I’ve always found the pi-calculus hard to understand, because the world it describes is not a world I feel at home in. It’s a world where agents create channels, send messages down these channels, receive messages, and act based on them. Mike tried to explain it to me using mailboxes. But it hasn’t stuck, yet.
Wikipedia gives this explanation:
Central to the pi-calculus is the notion of ”name”. The simplicity of the calculus lies in the dual role that names play as ”communication channels” and ”variables”.
The process constructs available in the calculus are the following: , where
, where  and
and 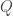 are two processes or threads executed concurrently.
are two processes or threads executed concurrently.
• ”concurrency”, written
• ”communication”, where
• ”input prefixing” is a process waiting for a message that was sent on a communication channel named
is a process waiting for a message that was sent on a communication channel named  before proceeding as
before proceeding as  , binding the name received to the name
, binding the name received to the name  . Typically, this models either a process expecting a communication from the network or a label
. Typically, this models either a process expecting a communication from the network or a label
cusable only once by agoto coperation.• ”output prefixing” describes that the name
describes that the name  is emitted on channel
is emitted on channel  before proceeding as
before proceeding as  . Typically, this models either sending a message on the network or a
. Typically, this models either sending a message on the network or a
goto coperation.• ”replication”, written , which may be seen as a process which can always create a new copy of
, which may be seen as a process which can always create a new copy of  . Typically, this models either a network service or a label
. Typically, this models either a network service or a label
cwaiting for any number ofgoto coperations.• ”creation of a new name”, written , which may be seen as a process allocating a new constant
, which may be seen as a process allocating a new constant  within
within  . The constants of the pi-calculus are defined by their names only and are always communication channels. Creation of a new name in a process is also called ”restriction”.
. The constants of the pi-calculus are defined by their names only and are always communication channels. Creation of a new name in a process is also called ”restriction”.
• the nil process, written , is a process whose execution is complete and has stopped.
, is a process whose execution is complete and has stopped.
My eyes tend to glaze over halfway through this explanation, because it involves too many undefined terms that are all being defined in terms of what they do with each other. These are mixed in with comments that are not really part of the formalism per se but supposed to be helpful, like “the constants of the pi-calculus are defined by their names only and are always communication channels.” These mainly make it harder to tell what’s the actual formalism and what are the side-remarks.
However, I think our research group should learn this stuff, and with Christian powering our effort I bet we can do it!
Good thinking, Daniel. Thinking of analogies for the pi calculus is interesting and worthwhile. (see Milner’s “The Polyadic Pi Calculus: A Tutorial”) The basic ontology is that there are independent agents which send and receive data over channels. This is fairly easy to imagine in general, but we need a more concrete description.
I think of agents in parallel basically as a community of automata, and channels as radio frequencies with rules for access. Agents tune to these channels either to talk or hear, and whenever both happen on a channel, a communication takes place.
COMM : x!(y).P | x?(z).Q → P | Q[y/z]
Both forget the channel, the “speaker” forgets the data, and the “listener” uses the information it receives, plugging it into designated holes into its “plan of action”.
That’s just the basic local event. It gets more subtle as one carries this further. What is the data, and what are the plans of action? Just more kinds of potential communication. The agents and channels are just parts of a larger program – the whole story is what happens globally. So to get an actual idea of what’s going on, we need an analogy robust enough to span both levels.
I haven’t found an explanation like this, and if one exists it could help everyone a lot. If not, it’s up to us to figure out how to explain it well. Looking forward to hearing people’s thoughts of how to understand this brave new world of computation.
The pi formalism somehow reminds me of the LabView programming language. Even though the language was targeted to control lab hardware, I used it for numerical simulations a long time ago because the language provided a transparent access to a 32-bit address space at the time the 8086 processor memory was tediously segmented into 16-bit addressable chunks.
I have hard time getting a hold of the formalism, like others, however.
So, I think I love this conceptually, although I struggle to see just how far-reaching it actually could be.
For me the problem already starts at properly grasping the pi calculus. Most explanations I found of it were rather opaque.
That being said, the paper on the rho calculus was relatively transparent, as I recall. It’s been a while that I read it though. (Pretty sure that was shortly after the previous time you brought up this project, unless I missed a few updates in between there somewhere) So I’ll have to read it again to remind me of how it works.
I also had attempted to build it in globular, but eventually gave up, coming to the conclusion, that it requires an infinite regress.
I think the issue was probably with the typing? I think the untyped version worked, but once types came into play, I had troubles formulating arbitrary function types in globular without infinite regress. Like, a -> b -> c worked. I could simply piece that (or arbitrary such chains) together from a -> b and b -> c, via straight forward composition. But (a -> b) -> c and similar, where a function requires a function as input to get a value caused issues. As I recall it was effectively because a function in globular would live one level above a normal value (unless, of course, that value also happened to be a function) and I couldn’t manage to get them to match such that globular is happy. If I were to get past that hurdle, I’m pretty sure I could implement the entire rho calculus in globular to toy around with it and get some better understanding of how it all actually works along with the typing.
This is great! We’d love to see the result, once you get it working in Globular. (everyone should check out globular.science , a great online tool for constructing proofs with string diagrams) Dr. Baez and I are very interested in exploring the higher-dimensional rewriting of the rho-calculus.
I’m sorry, but I’m not sure I understand exactly how there arises an infinite regress. To be honest I haven’t thought about constructing the type system by hand, but I want to learn about that process. Could you describe what you’ve done in Globular so far? Thank you.
So to be clear, this is the paper I attempted to build in Globular: https://arxiv.org/abs/1704.03080f – Specifically, I tried constructing the Rho Combinators of section 7.2 – the W-sorted ones as seen on page 9.
It’s not even particularly difficult, though it is rather tedious. Especially, because there is no polymorphism (At least I think that’s what I’d like to have) in Globular.
I managed to build everything, except for “for” with the type
N -> (N -> W) -> W
which takes an N, and a function from N to W as inputs to produce W.
My problem is, that, the way I have it set up right now, N and W live in a lower dimension than N->W. I can’t (as far as I can tell), make that work, except by making (N->W) an explicit type on the same level as N and W. But then, that (N->W), (once again, as far as I can tell), can’t be equated with the higher-dimensional usual N->W.
I must add, that I’m very much an amateur at this. My approach is basically playing around until stuff works. I did spend quite a lot of time back then, trying to make it work though.
I’ll have to think myself into this again, but here is what I had:
The most developed, but I think I actually went a dimension higher than necessary? I can’t quite remember anymore:
http://globular.science/1805.002
I’m pretty sure I actually had more, but I probably didn’t save some things in frustration. This is barely more than just the definition of each object. I did prove 0|P = P and P|Q = Q|P though. As you can see, “for” is missing altogether, for lack of ability to model it.
I ran out of time right now, but I’ll explain more later. Perhaps you can figure it out by then, but if not, no big deal. It is kinda convoluted to understand (I reckon) without any explanation.
Ok, I’m going as in-depth here, as I possibly can. This likely means, I’m telling you stuff you already know. I’m just not sure what is or isn’t important. Also, my own understanding is rather surface-level at this point, so I might bring up stuff that was confusing to me, but is painfully obvious to you. If that happens, I’m sorry. This also very much isn’t a polished project, as will become aparent shortly. It’s all very messy. Please bear with me.
So let me preface this with problems I ran into, and design decisions I made:
I remember having fiddled with the colors a lot, but because I restared several times (in new attempts to get “for” to work), I eventually stopped bothering as much. If you keep up due diligence to recolor everything sensibly instead of relying on default colors, many objects, especially the higher order ones, become a lot easier to discern.
The biggest problem, and a true show-stopper, is the afore-mentioned inability to represent “for” or anything that requires a function type as an input to another function type. I’ll go into this a little more later.
Another one is the lack of type polymorphism (I really hope I’m using that phrase correctly), requiring me to either cheat my way through the SKI combinators (which are no problem what so ever in the untyped setting), or build an impractical number of variations, one of each actual type combination. (I’m not sure right now, whether the necessary set for full coverage actally is finite. I guess that will depend on how “for” is ultimately represented.)
Then, there is the matter of convenience versus strictness. I could minimize the number of individual components I need by relying on invertibility. That also makes it easier to construct certain objects with shortcuts that would normally be illegal. For the sake of convenience, that’s fine. But you gotta be careful not to use these options unwarrantedly (i.e. during a proof), which could result in objects without actual meaning. – Mostly to keep things light and flexible, I opted to do just that. My 1-cells are all invertible, making higher cells easier to construct, but some nonsense is possible. In a finalized version, once all the concepts work as desired, you’d probably want to hand-construct those various caps and cups and what not so as to make abuse impossible. Correct By Construction and all that Jazz.
Though one of the things, that the invertibility of those 1-cells actually makes possible is arbitrary duplication and deletion, both of which are needed for the S, and K combinators, respectively. That’s one way how I could cheat my way past the lack of polymorphism. (I didn’t actually do that yet.)
And finally, there was a problem of dimensionality, and the way, Globular renders things:
Basically, I could make it happen in 2 dimensions, if I add several rules, such as the ability for strings to cross, by hand.
I could make it happen more easily in 3 dimensions, giving me most rules I need, but I still need to manually add rules, that strings can pass through each other. (“Interchanger” = “Interchanger Inverse”)
Or I could make it happen in 4 dimensions, and already have all those rules for free. But at the cost of Globular getting to the limits of its rendering and its user interface.
For this take, I opted for the 4 dimensional version which has the cleanest, shortest proofs (not requiring ridiculous numbers of steps from applying some of these manual rules), but a whole lot of extra fiddling with the interface, and mental gymnastics, to get it to do what you want it to, and to even figure out what you want it to do. (I’m pretty sure I already had 3 cell versions at one point, even with a few more proofs done. The interchange flip rule isn’t really that hard to add manually, and, at least for simple constructions, it doesn’t introduce too much clutter either, so perhaps that’d be a better trade-off in terms of convenience, compared to this.)
If these things were solved/improved, Globular could actually become quite excellent to visually design/hand-implement systems like these. (Assuming I – or anybody – find a way to get around the first problem, which may not be a globular problem, but a lack of imagination on my part.)
With all that out of the way, let’s walk through the simplest proof step by step, and in several projections.
That would be (P|0) = P.
So since my objects are up to 4-cells, consequently, proofs are 5-cells.
The most simplified projection level that’s actually interesting is Projection Level 2:
Slice 0: https://imgur.com/xIOp6md
This just says “if you have something of type W (red string) sitting in the environment (light blue surroundings), you can apply (P|0) = P (light gray dot) to it, to get another thing of type W.”
It’s read from bottom to top, by the way. Inputs go up into outputs.
Projection Level 1, Slice (0,0), and Slice (0,1): https://imgur.com/t90SV5T
The same idea, but this time as a cross section. You start with a string in the environment, and you end with a string in the environment.
This tells us very little. But Projection Level 2, Slice 1 actually contains the meat of the theorem:
https://imgur.com/K8c8O8P
You have two red strings, one of them seemingly starting inside the gray area, the other starting on the bottom of the environment.
Now, first off, the gray area is actually the boundary of a here hidden 4-dimensional interior. So really, the light gray dot is sitting in front of that boundary, embedded into the environment blue environment, just like the other string.
In Projection Level 1, Slice (1,2), you can see it from another side:
https://imgur.com/BZ95zYM
The gray area, in this view, is actually on the right side. The white area here is still not the inside.
To see that, we have to go all the way to Projection Level 0. And this is, where the way Globular renders things becomes an issue:
Slice (1, 2, 2), when hovering to change to Slice (1, 2, 3):
https://imgur.com/B7Wvm6B
We finally get to see the inside of “|”, with the previously white area now on the right. It’s pink.
Pink regions are ones that expect a W as input and give a W as output, as helpfully indicated when hovering over one of them: They’re called “W->W”.
There’s also a maroon boundary inside. That boundary is called “W->W->W” and it’s there to glue together two pink areas. Together, they are actally of type “W -> W -> W”, just as reqired for “|”.
In fact, this way, I can chain together anything to construct arbitrary types such as N -> W -> W -> N, etc.
But try as I might, I was unable to extend this to allow types such as the one required by “for”.
The concept I had in mind basically is somewhat like soap bubbles bubbles: Every input is the left side of a bubble, every output is the right side of a bubble. If you apply an input, you actually “pop” the left-most bubble, making the next bubble accessible. (Input always happens from the left.)
I experimented with allowing bubbles inside of bubbles, rather than only touching “from left to right” as shown in that slice, in order to model functions types as input, but I never got it to type check. The output would always come out wrong. I need some trick to satisfy globular to properly construct this.
And finally, there’s another issue here: Note the lack of red dots. That’s why I posted a transition slice. The yellow rectangle actually shows off how the 0-process would get added between Slice (1,2,2) and Slice (1,2,3).
The actual pi-calculus-titular Processes are entirely invisible at this projection level.
But the fact, that this rectangle
a) appears in the blue environment, and
b) is to the left of the left-most bubble,
means, that, in all the higher slices, the 0-process is in front of the “|”, right where that has its first input.
Since the 0-process already is in the right spot, it can be eliminated immediately, covering one branch of the “|”.
Ok, so that covers what everything is in great detail. Now, to the actual proof:
Back to projection level 2, slice 1.
Starting from the bottom (the links provide the corresponding slices of projection level 1 slice (1,n))
0) The arbitrary process P enters the environment. https://imgur.com/t90SV5T
1) Introducing a “|”, which is represented by two bubbles https://imgur.com/KY7ZTNe
2) Introducing a 0-process (already in input position, “in front” of the frontal bubble) https://imgur.com/BZ95zYM
3) Applying the 0-process to the input branch of “|”, eliminating both. We’re left with only one bubble, and P. https://imgur.com/hyl2Q6W
0 is of type W, “|” of type W -> W -> W.
Applying 0 to “|” yields the remainder of type W -> W, so only a single bubble of that type, and no W string, remain.
4) https://imgur.com/6i8f6XA and
5) moving P into position to be accepted as input. https://imgur.com/Se1tsQY
Globular always requires a lot of manual shoving around that doesn’t actually mean anything, computationally. You can only apply rules if you have an exact match, after all. The reason I have to get the processes into these specific spots is, that I defined the application operation that way..
6) Applying P to the remainder of “|”, leaving only something of type W behind. https://imgur.com/t90SV5T
Technically, I guess I’m not really requiring, that the output W be the same as the input W. I’m not sure if there is a good way to prove/require that from within globular. All of this is kind of in point-less and curried style, I think the terms would be. – I never have to name any processes I need. They are simply anonymous strings that are inputs to the environment. the only way to identify particular processes throughout, is to follow the strings.
I haven’t implemented the S, K, I combinators here yet, partially because of the mentioned lack of polymorphism. I need quite a lot of them. But the “Copy” and “Eat” cells are basically the start of that, corresponding to crucial sub-operations of the S, and K combinator, respectively.
Implementing them for any given combination of types would be really straight forward. But also very tedious.
I already implemented (untyped) SKI calculus in the past here: http://globular.science/1612.015v3
To give you an idea, what would be necessary to do there. Check out the 5-cell there, to see a proof of how a mocking bird ends in an infinite loop.
Go to Projection Level 1, Slice (1, 0), and then step through all he way to Slice (1, 45) to get a quick overview of how it all works.
To get a better idea of why it works, check out the various “apply” rules (always on Projection Level 1).
It’s conceptually far more straight forward than my rho-combinator attempt.
There’s also this vastly more extended version http://globular.science/1805.003 where I added a ton of combinators. I never published it before now, so that probably means, it’s unfinished. Though the Y-combinator works, for instance. That one’s kinda fun.
Basically, my approach to Rho combinators works in roughly the same way. Once everything works, you’d end up with the same kind of string constructions. Just with a bunch of function-type bubbles.
So to summarize:
What I have (in this version):
* The Unit Law (though incorrect because I used C instead of 0. Easy fix in principle.)
* Commutativity
What I could have (but I never got around to it):
* Associativity (should be rather easy)
* ϵ Evaluation
What I could have (but it’s a mess without polymorphism):
* σ S-action
* κ K-action
* ι I-action
* Most of the calculations in the appendix.
What I don’t have (unless I get a bright idea):
* ξ communication
* The second proof in the appendix.
(both of which involve “for”)
Thank you very much for this thorough explanation. You’re not being too obvious; I and many other people are not yet fluent in Globular. So, I’ll start with some basic questions.
Why are N (names) and W (processes) 3-cells? What are the lower-dimensional cells establishing, and how are they being used in the 4-cells?
Thanks; we really appreciate your demonstration.
John’s explanation is spot-on. Please read my reply to his one too!
Say, could you give me some kind of non-trivial but not too long program (in its initial state) written out in Rho combinators?
I think, if you see something like that, where you already know how it reduces step-by-step, as it’s done in (my implementation in) Globular, you’ll get the hang of it much more easily.
(Mind you, technically I should be able to represent any program that Rho combinators allow you to write, however, because I have to manually shift around wires, it’s actually likely much slower than even just writing down the solution by hand. So that’s why it needs to be simple.)
Christian wrote:
My vague guess is this. Globular deals with n-categories. Thanks to the periodic table of n-categories, a symmetric monoidal category C is really a 4-category, namely a 4-category with
• one 0-cell
• one 1-cell
• one 2-cell
• objects of C as 3-cells
• morphisms of C as 4-cells.
So, it makes sense that things that look like ‘objects’ in a symmetric monoidal category need to be 3-cells, and things that look like ‘morphisms’ need to be 4-cells. Then equations between morphisms, or more precisely proof of these equations, will be 5-cells. And below Kram writes:
We need a 4-category for the exact same reason our universe is 4-dimensional when you count time. You need 2 dimensions of space to have enough room to switch two things, but 3 so it doesn’t matter whether you move them by switching them clockwise or counterclockwise; then you need a 4th dimension for time. In other words, only when you have 4 or more spacetime dimension can particles trade places without their paths becoming tangled.
All this is explained algebraically, and generalized, by the periodic table of n-categories. James Dolan and I came up with this, and the cobordism and tangle hypotheses, in the most important paper I’ll ever write:
• John Baez and James Dolan, Higher-dimensional algebra and topological quantum field theory, Jour. Math. Phys. 36 (1995), 6073–6105.
That explanation is exactly right and (unsurprisingly) far better than I could ever have put it.
That being said, all of this can also be done in 3-cells, if you just add a single rule, namely, that wire crossings can flip order.
Also, I just thought about this more again (previously, I was just trying to explain what was actually going on in that globular session, not really rethinking my decisions), and I tried to remember, why I did all this bubble concept stuff in the first place.
As far as I can tell (it’s been months), I actually only did that in trying to fix the very problem, that evidently is not solved by this, namely expressing types of the form (a->b)->c and the like.
I’m not convinced, this could have ever worked out. I’m not yet sure, how else to fix it, though.
I just finished a complete untyped version doing away with that entire thing, and it’s far simpler and more transparent. This time I opted for 3-cells plus that mentioned extra rule. I’m going to do final touches (improving colors and such), then I’ll publish that and explain it. It looks much more like the other projects I linked on SKI combinator calculus. It also doesn’t have the monoidal structure of “|” inherently. (I can’t just derive them), but instead, those have to be implemented by extra rules.
Anyway, depending on how quickly I get to that, expect all that soon (today or, at worst, tomorrow, hopefully)
As a final remark, I’m not even sure Globular is intended to be used as I do here.
I put this in a new thread, because the previous ones already got to the limits of their depth, apparently. I hope, Christian Williams will find it here:
Here is a much simplified, untyped version of the Rho Combinator Calculus:
http://globular.science/1805.004
First, let’s go through the cells, level by level:
The 0-cell acts as the environment in which everything else happens. It merely acts as a background and has no other job.
I skipped 1-cells for convenience. To build a 1-cell out of a 0-cell, you have to take the 0-cell as source, and then again as target. To build a 2-cell out of a 0-cell, you have to take the 0-cell, apply identity once, and take that as a source and target. Any further identity application obviously will generate a resulting cell that many levels further up. More on that later.
There is one 2-cell that represents my single type “term”. I could have had another type “1” for all the combinators, as per the paper. But as far as I can tell, that would have had no advantage while making things needlessly complicated. However, this is also where one would go about adding more types.
Adding N and W is easy enough. The problem starts, once again, with “for”, which asks for a function N->W as input. The S-combinator is even worse, though. It asks for three arbitrary types Z->Y->X, Z->Y, and Z as inputs, and I think that means, X, Y, and Z don’t have to be just N and W. They could be arbitrarily nested functions of those two types, right? (If not – if there actually is a finite number of types that will ever be needed for any construction of interest, this suddenly is no longer a problem. Not an unsolvable one at any rate. You’d still have to provide one wire color for each type.) This is where type polymorphism in Globular would be extremely useful. I think that also goes against the idea that Globular only works with strict, finite categories, right? (I’m pretty sure type polymorphism would imply a category with infinitely many objects?)
The 3-cells are, where all the combinators can be found. At that stage, these are only names though. What makes them tick comes only later. You’ll also notice, that all of them seemingly have no input and one output. The reason for that is, that I chose curried style for these, much like in the paper. They are used like this:
https://imgur.com/9ERYRaC
(this example features the S-combinator with three inputs) Doing so makes manipulating diagrams much easier, at the cost of hiding, how many inputs any given combinator actually asks for.
The uncurried version of S (and likewise others) would have looked more like this:
https://imgur.com/3qwxb8R
and it’d always have demanded three inputs, unless I had defined several verions of each multi-input combinator with each combination of already given inputs or something like that.
There’s also three more 3-cells:
Branch is the stand-in for parentheses. This will also be crucial for connecting each combinator with its inputs. – It works exactly like it’s done in the paper. Your terms will look like the binary expression trees that correspond to the terms written linearly with parentheses. So then the example from before ( https://imgur.com/9ERYRaC ) can be written as (((S X) Y) Z) with arbitrary inputs X, Y, Z.
Copy is an intermediate construct, which comes up when applying the S-combinator. It duplicates anything below it. It’s unfortunately also part of the communication rule. That’s the one aspect I really dislike about the current implementation. More on that later.
Eat is an intermediate construct, which comes up when applying the K-combinator. It destroys anything below it.
Next up, 4-cells. This is the actual machinery. The rules of how all this stuff interacts.
The very first rule here, pass through, is a consequence of me choosing to implement the combinators as 3-cells. It allows for wires to pass through each other. 4-cells would have had this rule automatically, at the cost of reduced ease of use of globular. (It’s surprisingly usable with 4-cells once you get the hang of all the possible operations, but it takes a lot of getting used to first.) This is also why I skipped 1-cells. Had my wires been 1-cells, and the combinators therefore 2-cells, it’d have taken a huge amount of manually added extra rules to get all the necessary moves. And obviously, I could also have skipped 2-cells to get 4-cell combinators, 5-cell rules, and 6-cell proofs. Globular’s support for 5- and especially 6-cells is rather spotty at this point though. Their aim was to properly support 4-cells for now, if I recall correctly. And those work great!
After that, I modelled the three structural concurrence rules. (Also explicitly, this time. With this setup, I can’t actually prove them from other stuff.)
If you want to build stuff yourself, and you don’t actually need to make use of these rules, I highly recommend temporarily deactivating the invertibility of these. Especially of 0|P = P. That one is super annoying. A mis-click will often prompt Globular to just insert a random 0-combinator in that spot. You can get rid of it by clicking again, but it’s still annoying if it happens twenty times through a 100 step process.
Followed by the Reduction Rules.
S, K, and I are pretty straightforward. I just leaves its input alone, K discards its right argument, and S (from bottom to top)
https://imgur.com/i04UKdM
Then, the two big ones:
Communication is a mess. I really don’t like the fact, that there is a copy term in this initial state:
https://imgur.com/IBNnp7C
That little detail makes it somewhat brittle: If the P-input isn’t just a generic input, but actually has some further structure, the copy branch you need in this initial state would be able to go further down. So if you happen to not recognize, that you actually can use the communication rule, right now, if you continue copying beyond this point, it’ll be impossible to actually apply the rule. The one way to half way fix that would be to make all the copy rules invertible, so, assuming you didn’t do anything else besides copying, you could just undo the damage.
Globular demands exact (strict?) matches to apply any predefined rules. If things are off just a little, it’ll refuse to transform anything. Thing is, I don’t know how else to tell Globular, that the input here is supposed to be the same. One process is calling for P, the other can provide it.
For good measure, I implemented two slightly different versions of this rule though. In case you accidentally copied the &-combinator, you can at least still use communication’:
https://imgur.com/GPx4rKc
By comparison, Evaluation is actually pretty straight forward. It has an Eat combinator in its output, where it doesn’t matter. (If, somehow, it’d have one in the input, that’d be just as bad as having a Copy there.)
After that, it’s all the rules for copying and eating. Pretty repetitive. The only problem is, that every single constructor (other than Eat itself) needs a copy-, and an eat-rule. (Copy doesn’t need a copy rule either. Though it does need a left and right eat.)
And finally, the six computations are given, as found in the Apprendix. [[P]]_x and such are translated as (K P) to make it work, as the paper suggested.
These 4-cell identities each have a corresponding 5-cell proof, constructing entirely with already existing components, a way to get from the starting configuration to the ending configuration.
Let’s pick one of them and step through the proof in relative detail.
I’ll go through the one I called “Appendix 3 Proof”.
Here is the starting configuration:
https://imgur.com/4TmV133 (Projection Level 1, Slice (0,0))
which is, I think, actually far more readable than:
(((S((S(K !))((S(K &))(K P))))(K Q)) x)
Here is the end configuration:
https://imgur.com/GbAawSr (Projection Level 1, Slice (0,1))
which is about as readable as:
((!(&P))Q)
The Eat cell stands in for “stuff to be removed”, so it doesn’t show up in a hand-written term. You can’t get rid of it, though, because else, Globular would complain about a mismatch. There were three inputs before. Can’t end up with just two in the end. I suppose, the computational equivalent would be something like “To Be Garbage-Collected”?
Now, let’s look at the overview of the entire proof. (Projection Level 2, Slice 1):
https://imgur.com/0xyEnGe
It’s hard to read at this size. I recommend checking it out yourself, zooming in from within Globular, to see it more clearly. This is basically a map of the entire proof. You may notice, that there is one single superfluous step (ironically, it’s an accidental application of the extra rule, “pass through”), that I can’t easily get rid of (I think), without basically rebuilding at least half the proof, so let’s ignore that.
Otherwise, I believe this proof to be optimal. Cerainly, the individual wires all pretty much just move in one direction, if at all, suggesting it’d be hard to tighten them up any more.
For the sake of getting used to this view, I recommend going back and forth and comparing how each move of
Projection Level 1, Slice (1, i)
as you step through all n slices, starting with 0, corresponds to each change in the diagram of
Projection Level 2, Slice 1
when read from the bottom up.
So, back to our starting configuration:
Projection Level 1, Slice (1,0)
https://imgur.com/4TmV133
At this point, the only possible operation (disregarding moving around wires in arbitrary ways) that can actually be done is, to apply the S-combinator in the top left. It’s the only combinator on screen, that has all (three) of its input and, therefore, can be applied.
Hovering over the 0 in the slice overlay reveals, that that’s precisely what’s going to happen.
After actually doing that, we land on:
Slice (1,1): https://imgur.com/G4dTRDd
The S-combinator is now gone and, in its place, we get a new wire interchanger, and a Copy.
No combinator can be immediately applied now. Something first has to be moved into the appropriate situation. If you check carefully, you’ll find, that only the next lower S-combinator is going to be reducible.
So let’s move things around a little, until…
Slice (1,8): https://imgur.com/kJF3KBL
that S-combinator once again is in position to be applied.
Note, S-combinators always need at least three Branch-es directly adjacent like in that image, to be successfully applied. (That’s because of the way I defined it, although I think it’d be hard to come up with anything else, given the way I built everything.) After doing that, we get to
Slice (1,9): https://imgur.com/jRUphgu
where, once more, no combinator is immediately applicable. But the top-most K-combinator looks rather promising now. K-combinators are always nice, because they tend to simplify problems. So, let’s move around stuff, until this one’s in position as well:
Slice (1,18): https://imgur.com/RuTXPxY
It may well have been possible to move a whopping four Branch-es into position adjacent to the K-combinator, but it only takes two inputs, so the minimum amount of work required to do the trick ends in this configuration. So let’s apply:
Slice (1,19): https://imgur.com/e7KQObJ
There now is an Eat, which will, after a little moving (this was also where I made the mistake of superfluously flipping the interchanger, so from here on out, one slice fewer would have been strictly necessary.)
Slice (1, 21): https://imgur.com/vI5L6i5
be able to delete the left branch of the Copy right under it, significantly simplifying the structure overall:
Slice (1,22): https://imgur.com/BdKEPaq
Next, more moving will bring the final remaining S-combinator into position:
Slice (1, 31): https://imgur.com/uhSMvI0
to be applied, giving us another Copy.
Slice (1, 32): https://imgur.com/NIQ09eq
A bunch of moving around…
Slice (1, 41): https://imgur.com/mwRNOfq
… will bring another K-combinator into position,…
Slice (1, 42): https://imgur.com/Gkw8QIe
Slice (1, 43): https://imgur.com/KT8ongS
Slice (1, 44): https://imgur.com/P4N0bwv
… ultimately removing another Copy. More reconfiguring will eventually…
Slice (1, 51): https://imgur.com/vzvGGxP
… get us another K-combinator into place, deleting the final Copy:
Slice (1,52): https://imgur.com/ybjHyyI
Slice (1,53): https://imgur.com/yzp2mlO
Slice (1,54): https://imgur.com/uA9mBGV
A final little bit of shuffling around:
Slice (1, 58): https://imgur.com/V6380kP
And the last remaining K-combinator can also be applied, bringing us to our end configuration:
Slice (1, 59):
https://imgur.com/GbAawSr
Is this take clearer now? This is tedious, but it’s actually quite straightforward. A few improvements to Globular, and much of the tedium could actually be done away with as well!
(My wishlist for convenience features includes such things as continuous-drag, so things can be moved further than a single step with one drag motion whenever the action in question is the same one over and over; multiple views – why not (optionally) have two or three projection levels or slices up at the same time?; and (optional) 3D views, which probably would help visualize a bunch of structures that currently are really hard to grasp, especially for higher cell levels.)
Nice stuff, Kram! You may have revealed a problem with trying to implement the ρ-calculus in Globular:
Right, actually they could probably be arbitrary terms built from all the combinators in the language. I say “probably” because I don’t know the ρ-calulus. But in the SKI calculus, a term is recursively defined as either S, K, I or something of the form (t t’) where t and t’ are terms. Then, given any term of the form
(((S t) t’) t”)
we are allowed to rewrite it as
((t t’)(t t”))
I see what you mean: saying we can rewrite (((S t) t’) t”) as ((t t’)(t t”)) is not a rewrite of a specific expression; it’s a rewrite rule that applies no matter what t, t’ and t” are. And this may go beyond the scope of Globular.
Globular works with semistrict finitely generated n-categories. It’s dealing with n-categories rather than mere categories because it allows cells of many dimensions, not just 0 and 1. They’re semistrict rather than strict because while associativity and the unit laws hold as equations, the interchange law holds only up to isomorphism. Most importantly while the user can only specify finitely many generating cells (as far as I know), there is no limit to how many cells can be built from these. For example if you have one 0-cell x and one 1-cell f: x → x then you instantly get infinitely many 1-cells f2, f3 etc.
But all this does not work against your main point, which is that we might need some greater flexibility to express the ρ-calculus or even the SKI calculus. This would not be surprising: nobody has ever claimed to be able to work with cartesian closed categories (which capture some aspects of the SKI calculus and λ-calculus) using just finitely generated n-categories.
Thanks!
The way I implemented this, it wouldn’t bother me at all, that inputs could be made from arbitrary combinators. This is all point-free (I think the term would be) in that all the combinators don’t even care what’s below them: If they are in the right context to be applied, you can apply them.
If you check the action of the S combinator, all it requires is three branches in a row, directly above it to the right. Other combinators don’t even play into it per se. Literally all it does is rearrange the wires
All I care about (or would, if this were typed), is the color of the input wire. If that is appropriate, then the connection can be formed. Otherwise, assuming I’d implement all the rules in the right ways, Globular wouldn’t even let you build it, thereby enforcing the type constraints.
But still, we’d need infinitely many such wire colors – an infinite family of them, to do it.
With pure SKI combinator calculus, at least if you don’t care about the types, that absolutely works fine, actually. And with the caveat of that one annoying Copy in the communication law, so does this untyped rho combinator calculus, really.
The second I could somehow conveniently write down infinite families of cell types in Globular, I think everything would be doable just fine.
On that note, by the way, I actually updated the globular session:
http://globular.science/1805.004v2
It’s now 4-cell based again, thus with one fewer explicit rule
cleaner. (For instance I fixed the superfluous move I mentioned before.)
If you just increase all the cell numbers (except for 0-cells) by one, the previous explanation pretty much still applies in exactly the same way though.
Turns out 6-cell proofs aren’t a problem for this kind of thing. (Or maybe an update has made Globular more robust since. I thought I remembered running into problems in the past.)
You made a good point there about types, Kram, but I exhausted myself moving your comment to the correct location in the thread, which can be done only using dirty tricks.
By the way, what experienced blog-commenters do, to keep the column from getting ever thinner in long discussions, is to hit the Reply button not at the bottom of the comment you’re replying to, but at the bottom of the comment that’s one less indented than the one you’re replying to.
It’s a tree structure. Maybe this will make it clear: to be just as indented as the person you’re replying to, you don’t want to be their child, you want to be their sibling!
I took this approach just now: that’s why this comment isn’t more intended than yours.
This isn’t necessary for short discussions. But when the column gets so skinny that you don’t even see a Reply button at the bottom of the comment you’re replying to, this is clearly mandated!
This may sound complicated, but it’s not as hard as working with 5-categories.
Kram wrote:
Okay, I think I got it. I think you’re saying Globular is powerful enough to handle the untyped SKI calculus (which is the original one, by the way); it runs into problems only in the typed situation, because one wants polymorphic versions of S, K and I.
For category theorists (only), a simpler and more familiar example shows up in weak monoidal categories. One often speaks of “the” associator in a weak monoidal category, but really for any triple of objects there is an associator, a morphism
there is an associator, a morphism
If one wanted to implement weak monoidal categories in Globular right now, one would (apparently) need to explicitly put in separate associator for each triple of objects, which becomes annoying when there are more than a few objects, and really annoying when there are infinitely many.
I suspect that this sort of “polymorphism” could be developed on top of Globular, but that right now Jamie Vicary is focused on getting cells of arbitrary dimension to work in a nice way. (At Leiden he mentioned some big progress he’s made in that direction.)
Ok, I will reply this way from now on. (Modulo the occasional moments where I flat out forget to do so – sorry in advance)
Thanks for fixing everything!
That being said, the indentation itself isn’t really a problem to me. It’s the lack of ability to reply at all (the button literally ceases to show up) once the reply depth has gotten to a certain level. (It’s not, that the button would have to disappear either. It’s on the left side, and the column is definitely far wider still, than would be required for that button)
If that’s by design, then perhaps this should already happen earlier (“Reply” should only show up at the top level), so what you suggest becomes the only possible course of action.
Yup, that’s exactly what I’ve been saying. That’s what I meant by type polymorphism, too!
I’m really sorry if my not really having the lingo down makes it difficult to follow my ramblings. One of these days I really need to study all that stuff to full understanding of at least the basics. I’m currently kind of taking an engineering approach to these things, I guess: Try stuff until it works. So my language is definitely not as precise as it could be.
In your weak associatior morphism, was the s on the right hand side intentional? Or was that supposed to still be a z?
Proper infinite dimensional cell support sounds great! Structurally it definitely looks plausible.
I’m cooking up a potential solution for typing now, by the way:
Can’t define infinitely many wires? Put arbitrary numbers of beads on them!
Instead of a wire ——– which has type N->W or what not, I’d get a wire with beads –o–o– the first of which is an N, the second a W.
Branches, then, would be “locked” first, and only if the beads on the left and right side match, would they let things past them.
Basically, in doing so, I’d build a type checker in Globular. By the end, in “fully checked” configuration, the types would be removed again, but it’d only let you remove all the types if there is no type error.
I guess that’s kind of equivalent to a run time check, so it’s not pretty and perhaps overly complicated. And specifically the S-calculator still poses some challenges with that approach (all other potential trouble makers – “for”, K, and I, will definitely work just fine that way)
Even without those extra troubles, “really annoying” is definitely a good way to put it.
Nevertheless, that ought to at least be possible given the current state of Globular.
And as another project in parallel, I’m also trying to think of ways to present the Rho Calculus in ways that emphasize more the distributed nature of it all. I already have a few concepts down. What I need to look into is how to make processes identify each other. (Basically, to avoid the aforementioned annoying Copy in the Communication rule) – once I have a good handle on that, I think the (untyped) Rho Calculus will get another structurally very different representation more “in the spirit” of it all.
I’m not sure yet, but that might then end up being the actual Rho Calculus. Not the combinator version.
(a typed version would likely end up having the very same problems as the typed combinators though)
Both of those projects are likely gonna take a good while longer. With any luck they’ll be ready once news surrounding rchain and Rho Lang pop up again.
Perhaps the people who designed WordPress thought conversations should only continue past a certain point if the people involved were smart enough to figure out that they should go back and hit an earlier “reply” button.
Seriously, it’s a weird design flaw. I can adjust how many iterations of indentation are allowed (if it gets too high, the text gets absurdly skinny), but I don’t see anything I can do about this.
No, that should be a z: we’re just moving the parentheses. I’ll fix it.
That’s clever. If it works, you’ve figured out how to prove an interesting mathematical result: something about how to emulate polymorphism in a system without it.
Hmm, “run time check” sounds familiar, so maybe a version of this mathematical result is well-known in theoretical computer science, but since you’re working with Globular I’m seeing it as a result about n-categories, and it might be new in that context.
However, it’s making me feel you should join the Globular design team and help them implement polymorphism in a really good, built-in way!
But it’s easy for people to feel other people should do more: I can see why you might want to keep this at the level of a hobby.
John wrote:
Well, I guess it’s sort of more like compiling.
Basically, what I’d do is:
Branches are locked at first. They need to be satisfied that input types match on both sides.
Types, as said, are represented as beads on those wires.
I’d basically build it such, that if a bead on the output wire and a matching bead on the input wire both hit the top of the branch, they can be deleted. (If there is a mismatch, the system would just lock down)
If the beads are all sifted through (currently I’m thinking of doing it with a special “unlock bead” that’s also needed on both sides), the branch becomes unlocked. It also propagates the appropriate output type (again encoded in beads) for the next locked branch to worry about.
The reason I’m saying it’s sort of like a run time check is, because the system actually doesn’t disallow you from constructing stuff with mismatching types. It only doesn’t allow you to actually execute them, because types can’t be entirely eliminated.
The end result, however, would actually be a completely untyped wire diagram again. Once the last bead is removed, and all the typing information is therefore eliminated, the same stuff would just work, that I already got to work now. It’s like, “check, that it makes sense once. Then forget why it makes sense and just accept, that it does.”
That’s sort of like the optimizations a compiler would do, right? If the types aren’t run-time relevant, why keep them around? The compiler already made sure it all works as specified. Just trust the word of the compiler!
If the types can’t be eliminated, the compiler will also tell you that (by never producing an executable, and perhaps by giving you hopefully useful error messages so you can fix things).
It’d actually be inspired by a simple Zero/Succ-based arithmetic calculator I built in Globular before. The difference really just is, that I’d have to deal with far more complicated rules (especially for that S combinator), and not just one bead type N->N (and a final bead capping off a wire, that’s 0:N), but several.
I’m not entirely sure my result would constitute a generic proof though: I think it’ll be inevitable to build very specialized beads just for the sake of getting the S-combinator to work. It’d most likely be more like a proof of concept (an existence proof) than a scheme you could follow step-by-step (a universal proof) to make any sort of situation work.
As for joining the development team, I guess I could do feature requests. Which, I’m sure Jamie Vicary already gets more than enough of. (In fact, some of the features I’d like to see have already been suggested by others)
And perhaps I could do beta testing.
For actually contributing to the code base, I’d have to learn to write in JavaScript (and possibly CSS) first. Never really dealt with either.
(I probably could do that. Currently I’m mostly a Python-guy, with a side-eye to, but never actually having taken the plunge into Haskell)
If he really is working on a generic extension of the cell structure all the way to infinity, I think that’s very much something that ought to get priority over stuff like polymorphism. It seems more fundamental to me. Once that stands, all kinds of neat bells and whistles might be (relatively) straight forward to add.
It’s great to see this nice discussion developing.
Globular lets you work with any finitely-presented algebraic signature up to dimension 4, as long as the terms are purely compositional — that is, you can’t use any universal constructions, like cartesian products. For example, it lets you encode any finite PROP. Looking at Mike’s and Greg’s paper, I don’t see any clear statement that their syntax forms such a structure, so it’s not clear to me whether or not Globular is capable of encoding it. It’s possible that Globular can only encode some fragment of the theory, which may still be interesting; in that case, it would be good to be clear exactly what fragment this is.
At the moment general feature development of Globular is frozen, while we develop the next iteration, which will allow computation in infinite-dimensions. (I’m working on this with Christoph Dorn, Christopher Douglas, and David Reutter.) But don’t let that stop you posting feature requests for discussion on the issue tracker, for potential future inclusion.
Also, these proofs look great, Kram, thanks for sharing them!
Jamie wrote:
That’s more or less what I figured, and I’m very much looking forward to it! Thanks for your work! Even in its current state, it’s a great help to me, for understanding things simply by building them. And it’s quite incredible, what’s already possible.
As said, many of the features I’d like to see have actually already been suggested by others. But I’ll be sure to add new suggestions, as I spot them. I’ll have to read through the tracker again first, though. (Or is there another place to put suggestions besides Github? – That page apparently hasn’t been updated in a while.)
I’m not sure, I fully understand every implication of this, but it seems to me, that a large set of combinator calculi fit this description.
Generally, combinators appear to map quite nicely to Globular as string diagrams similar to how I defined them. All kinds of combinator calculi are possible, actually, as long as the rules don’t become too crazy. (For instance, I once tried to make SF combinators work, but the F-combinator is really challenging, due to its complicated, case-sensitive application rules. I think it might be possible, and I did get part of the way there, but I’m missing edge cases.)
At a guess that’s because combinator calculi very often are finitely representable (everything can be done with just the finite set of combinators), and compositional. (Any (if required, well-typed) string of combinators and balanced parentheses will be a valid program).
I believe, the three helper objects I need to make it work – Branch, Copy, and Eat, are rarely avoidable. Almost any combinator calculus should be realizable using only those three in addition to the actual combinators. (BCI combinators, being linear, would only require Branch. I’m not sure that one could ever be gotten rid of in a practical manner.)
Unless you have really exotic rules, which certainly is possible.
(There surely is a way to make that mathematically precise. What rules can or can’t be done? What combinator calculi admit these constraints?)
As previously explained, Branch is really the same as parentheses.
If I got that right, it should have the type:
Branch: forall X, Y : (X -> Y) -> X -> Y
Meanwhile, Copy and Eat come up in the S- and K-combinators. Since those are some kind of almost minimal set of combinators, presumably any universal non-linear combinator calculus will need these.
These have the types:
Copy: forall X : X -> X×X
Eat: forall X: X -> 1
I believe, those are the two morphisms a comonoid would have, right?
The 4-dimensional part is also nice in that, usually, I’ll want strings in such a diagram to pass through each other freely, which is best done in 4-cells, where all the relevant rules to manipulate them already are present.
Well, as said, if the Rho combinators can do it (and my understanding is, that they are a full translation of the Rho calculus), what I did thus far will be able to do it as well.
I also already mentioned the caveat in the communication rule. There is an input-side Copy instruction there, which copies an input in order to declare it the same. This is brittle, because it relies on you not copying something, in order to instead apply the more complicated, and thus perhaps easily unnoticed communication rule. As yet I don’t know how I might make somebody prevent the application of Copy, when they probably would like to do a communication instead.
(* more later)
Specifically, what’s happening is this:
The communication rule states:
((| C) ((| ((for (&P)) Q)) (( ! (&P)) R)) )
->
((| C) (Q (&R)) )
Or, with fewer parentheses:
C | for (& P) Q | ! (&P) R
->
C | Q (&R)
Where P is a process, &P is it lifted to a name.
So
! (&P) R
I think, basically calls out “I have something called P!
and
for (&P) Q
says “If I get something called P, I can interpret it!”
And so, R can be communicated as input to Q, which interprets it into another process Q(&R).
The problem is, that (&P) comes up twice. The way I implemented this, inputs are essentially anonymous. (Hence, say, S can be applied without caring about what’s below at all!) – so the only way (I can think of), to tell Globular, that two inputs are actually the same input, is by copying from a single input.
And presumably, without typing you could build nonsense, such as, I don’t know,
((| C) (& P)) = C | &P
which the types would rule out, because &P has type N (and P has type W), but | only takes things of type W to produce another W.
That’s clearly a flaw with the current design. But one that’ll be really hard to adress without polymorphism support (as per the previous discussion).
Other than those two issues, my current understanding is, that this is an entirely faithful, complete translation of rho-combinators, and therefore of rho calculus.
I might be mistaken though.
In summary, it should have the full power of rho combinators, but it lacks a few necessary constraints to make possible only legal trees of them, and to transform legal trees into ones that still are legal (i.e., they can still reach the same normal form).
Finally, I suppose, since inputs can’t be completely deleted, only “marked for deletion”, it could be argued, that the translation isn’t so perfect after all, even if the above problems were to be sorted out. But that seems like a non-issue to me. If really necessary, I could always just cap these up on the bottom (input-side) as well, thereby allowing me to actually delete inputs. Mostly that just seems like making things less clean though.
And arguably, knowing how much was thrown away could also be of interest.
(*)
There may be better ways to do the communication rule, but I’d have to have more of an intuition for when any of this even comes up.
Like, the SKI combinators themselves are already Turing complete, right? In principle, I could literally just ignore all the fancy new combinators, and build arbitrary programs in SKI combinators.
And I have a vague intuition for how programs look like when using SKI combinators.
I don’t really have an idea at all for how the same stuff looks like in pi or rho calculus. Or how you’d typically use any of the new elements.
Until I have that, it’s very hard for me to gauge the actual needs which, then, could further inform the design.
For instance, if it turned out, that the availability of communication can easily be gauged, I could potentially constrain Copy-nodes to be sensitive to that. You then could no longer make a premature copying error.
The most obvious idea I have to that effect is, to simply not allow copying &-combinators until communication can be ruled out. But I’m not sure that’s either necessary or sufficient for avoiding these issues. The types ought to allow it at least.
Kram wrote:
Jamie said “finitely presentable”, which means something precise.
It’s a bit tiring to say exactly what a finitely presented n-category is, but it roughly means:
1) There are finitely many generators – j-morphisms for various j from which which all others can be generated using he operations that every n-category has.
2) There are finitely many relations – equations been j-morphisms, from which other equations can be deduced.
In general, a presentation is a collection of generators for some algebraic structure, together with a collection of relations. We say an algebraic structure is “finitely presentable” if it has a presentation with finitely many generators and finitely many relations.
The classic example is a finitely presented group, and whenever people talk about “finitely presented” algebraic structures this is the paradigm they have in mind. In a group, the ways you get to “generate” new elements from old are multiplying two elements and taking the inverse of an element. In other structures, you get to do other things, which must be carefully specified.
Thanks for the explanation, John.
So in this example, would the generators be the combinators, and the relations their various rules?
As far as I can tell, I have:
An object env
(implicitly) the identity morphisms
1_2: Id(Id(env))
1: Id(Id(Id(env)))
A morphism of wires T: 1_2 -> 1_2
a bunch of morphisms of type 1->T, which are my combinators
three extra morphisms
Eat: T -> 1
Copy: T -> T×T
Branch: T×T -> T
from which all valid (and as yet some invalid) programs can be built (I think)
and, defined with all these, morphisms one level up, that give me the relations between them, from which all other valid equations can be derived via appropriate usage of composition and identity.
What would the j be here? Simply the cell level? Or perhaps one less than the cell level? (I.e. do you count what dimension the morphism lives in, or objects of what dimension the morphism connects?)
Or is that something entirely else?
Because I wasn’t sure, I dropped the j in the above.
Quick googling found me this as first/best match: https://ncatlab.org/nlab/show/J-homomorphism but I don’t know if that’s related.
Unrelatedly, I stumbled over this:
https://ncatlab.org/nlab/show/Lawvere+theory
Which may give a more general answer to Jamie?
Lawvere theories are categories with finite products.
It might be, that the group in question must itself be finitely presentable for it to work? But either way, that at least sounds like it will mostly satisfy Globular’s constraints.
That being said, we’re dealing here with Graph-enriched theories, about which the paper by Michael Stay and L.G. Meredith ( https://arxiv.org/abs/1704.03080 ) states:
and
Meaning, we’re still dealing with finite products.
We’re also dealing with multisorted Lawvere theories, and that’s a tougher nut to crack. To get the full, correctly typed (/sorted) theory, we seemingly need infinitely many sorts.
My upcoming approach is, to try to make that, too, work by exploiting the fact, that we are only talking about two generator sorts, W and N, here, so perhaps I can finitely represent all the required sorts. (The biggest challenge here will be the S combinator)
Interestingly, about the sorts, the paper also states:
The set of sorts is also finite. Presumably, things like N->W aren’t counted as sorts in that set, then.
Finally, the very first sentence of 4, states:
Which is vaguely related to my statement above, that most combinator calculi should admit a similar embedding into Globular, because the most interesting ones are finitely generated.
Below that, it states:
And after that, it presents the SKI combinator calculus as a Gph-theory, doing, as far as I can tell, pretty much 1:1 what I did.
(My single wire is the mentioned set of sorts, the various combinators and the three special morphisms are the set of term constructors, and after that I have the set of equations and reduction relations)
So while I absolutely might be missing something, I think that should pretty much answer Jamie’s questions about whether this work can be represented in Globular.
Hi both, thanks for your comments. The notion of Lawvere theory is definitely a related concept: it describes a finitely presented monoidal category with products. This is similar to what you can do in Globular, except Globular doesn’t know about products. The more appropriate that Globular generalizes is PRO: finitely presented monoidal categories without the property that the monoidal structure is cartesian.
Thanks, Jamie. I see.
As far as I can tell, the paper does require products here but only explicitly shows them here (minimal paraphrasing):
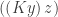 is shorthand for
is shorthand for 
Which clearly features a bunch of products.
But I believe, all that is, is a different way to write down the following diagram:
https://imgur.com/5VVTHlV
Read the picture from bottom to top and, in parallel, the above equation from left to right:
At first, I have two inputs T×T (i.e. composed side by side).
Then, left of that, I introduce a combinator, making it 1×T×T
It’s the K combinator, which has a single output wire, so now it’s T×T×T – three wires side by side.
Next up, I hit a branch of type T×T->T (or, curried, T->T->T), combining the two wires on the left, so as I cross that, I end up with T×T again.
Finally, I hit another branch, combining the remaining wires into one, giving me just T.
Here I did an overlay, trying to line up how the equation and the diagram correspond. Due to the way Globular lays out things, it got a little cramped in the bottom half.
https://imgur.com/0A9hfbw
So if I’m right, I essentially emulated products, to the extend they are needed here, by horizontal composition.
(Or it would be horizontal composition, if I hadn’t skipped two cell levels to get better-behaved wires. – Throughout the paper, they write, that it only requires 2-categories to model all this. And if I manually added all the wire interaction rules like interchange laws and such, which Globular gives me for 4-categories, already at the 2-cell level, it’d be true for my implementation as well.)
Horizontal composition is the 2-category version of the composition already available at the 1-category level, right? If I’m not mistaken, it’s the vertical composition that’s new. Or did I get those turned around?
Regardless, meanwhile, vertical composition is used for introducing all the relevant structures which, in the above equation, show up as various morphisms.
In the overlay version of the image, horizontal composition is blue, vertical composition is red.
The entire rest of the paper doesn’t reference products at all, as far as I could tell. It’s all hidden behind the various strings of combinators and parentheses as, apparently, a form of syntactic sugar.
Kram wrote:
That’s the idea. Whether Globular has the expressiveness to generate everything you want from these generators, and derive all the rules you want from a finite set of relations, is an open question. It can only generate new things from your generators using the operations in a semistrict n-categories, and similarly it can only derive new rules from the relations you state using the rules of a semistrict n-category.
There are many different kinds of logical system, with varying amounts of expressiveness. Globular is intentionally close to the bottom of the expressiveness hierarchy except in one respect, namely it allows a higher “n” (as in n-category) than almost any other system. So, I’d be surprised if the expressiveness of an ordinary computer programming language, even a simplified one like the lambda-calculus or SKI combinator calculus, can be captured by Globular. But who knows? Maybe I’m confused.
Right. I should just emphasize, though, that “expressiveness” is not the same as “computational power”. You can click the link to learn more about expressiveness, though probably not the really good math stuff. Suffice it to say that expressiveness is one reason most people prefer C+ to machine language, even though both are Turing complete.
Jamie wrote:
Don’t jump to that conclusion: the phrases “algebraic signature” and “purely compositional” are crucial here.
Right—and n-categories don’t have finite products unless you demand that they do, and Globular doesn’t allow you to demand that, so Globular probably can’t do all sorts of stuff that Lawvere theories (or graph-enriched Lawvere theories) can do.
Finite products are a key aspect of “expressiveness” that Jamie is deliberately _not _trying to include. You will be tempted to use finite products whenever you’re trying to duplicate or delete data: that’s what they’re good for. And that’s where you’re likely to run into a wall.
I would have to really carefully examine what you’re doing, to see if you’re somehow getting around this wall. Unfortunately I don’t have time.
As Jamie noted, you can use Globular to handle finitely presented PROs, and I believe you can also use it to handle finitely presented PROPs. PROPs are in the same ball-park as Lawvere theories, but they’re less expressive. For example there’s a Lawvere theory for groups, but not a PROP for monoids, because groups have an axiom
in which the letter is duplicated on the left side and deleted on the right side.
is duplicated on the left side and deleted on the right side.
This is a long, fun story but I’ve told it too many times in my life to tell it again now.
A random other issue:
The same as the cell level. A “j-morphism” is a “j-cell” is a “cell of dimension j”, where j = 0, 1, 2, 3, …
I meant to ask: What syntax do you use to get hyperlink text?
I know some versions of Markdown have a neat and tidy syntax for that. I could, of course, also use HTML to accomplish it.
But Markdown hasn’t really been standardized, and several subtly different versions are floating around, so saying “You can use Markdown” isn’t very clear. Is there a guide to the specific version of it, that you use on this blog?
I’d love for somebody to tackle that question, because as far as I can tell, the answer would necessarily have to clarify these combinator calculi in some subtle way:
I faithfully built all the objects and all the rules. I don’t see what could possibly be missing. If anything is missing, it ought to be something really subtle.
At best, the whole thing may be underconstrained because certain actions the current construction allows may lead to invalid states. – But most of that is the typing problem. The actual untyped version of these calculi would allow those exact same problematic states.
The one exception sill is that instance of Copy in the Communication rule, as I already established.
But in the SKI calculus? I’m pretty sure there’s literally nothing. – Essentially by construction. The pieces come together to generate the exact same behavior as the actual calculus would. No deviation is possible. The biggest difference is, that I have to do several extra steps (rearranging different combinators) to get everything in position to be able to apply stuff in the first place. But as long as we’re dealing with finite programs – no infinite rearrangement moves are required – this ought to work out.
I guess, that could ultimately be the limitation? But infinitely large programs (in terms of symbols, not in terms of rewrites until halting, i.e. infinite loops) seem like a relatively minor edge case not to have.
Or if there is no limitation of any kind, that ought to have some rather fundamental implications within category theory, right?
I’m not sure how to prove any of this though. All I can definitely do is: Show me an arbitrary valid string of SKI combinators. I can implement it in Globular and arrive at the same final form (assuming the string halts) as any other correct implementation would. (And if it doesn’t halt, I’ll run into the exact same loop. Also, where execution order matters, it’ll matter for me as well.)
I’m not quite sure what would have to be shown exactly. What conditions would I have to check to show, that this Globular implementation is fully faithful? If you have more insight into that, do you think you could give me a rough outline? Maybe I could actually do at least parts of such a proof.
I know. I didn’t mean to suggest that. My point just was, if my goal is to compute arbitrary things, without any constraints on how easy or practical or what ever else it is, the SKI combinators alone would already be sufficient.
That was me saying I’d really like some simple, small, proper examples of using these combinators to accomplish something that would be really hard to do with just SKI combinators, just so I could get a feeling for how these rules actually work in practice.
Like, what’s the “Hello World” of rho-combinators?
Oooh, ok, that’s actually helpful. This may well be it.
So for the most part, I do not have problems with duplication or deletion. That’s what Copy and Eat are for, after all.
I do run into what migh be considerd a problem at the very end though:
Globular always (sensibly) demands the same number of inputs. To accomplish that, I cannot copy raw inputs:
I can’t tell Globular to make this:
https://imgur.com/KDfWrLo
be the same as this:
https://imgur.com/1w7qbln
Similarly, with Eat, I can’t tell it to make this:
https://imgur.com/2koCBQB
be the same as this:
https://imgur.com/5gse58m
That being said, to me that’s almost a feature: It preserves composability.
If you have some arbitrary program P where a bunch of Eats and Copies are left at the very bottom, at the inputs, if I then decide to take some other arbitrary program P’ , the outputs of which would become inputs of P, it’d still work. Globular basically can evaluate a program all the way to the point where it will tell you how often each input is used. I think that’s actually useful to know?
Inputs that end up being just an Eat are ones that are used 0 times. – In the usual SKI combinator calculus, you would just drop these altogether.
Inputs that end up being a bunch of Copies are ones that are used n+1 times with n instances of Copy directly at that input.
In the usual SKI combinator calculus, each input would have be written as a variable labelled “x” or something, and so copying it is as simple as writing it down multiple times in various spots.
A fully reduced program in my Globular implementation might end up looking something like this:
https://imgur.com/5LoYmw5
(Usually you’d also have some combinators, but this is a possible outcome.)
which is equivalent to something like
(((((x((((x(((x((x(x)))))))))))))))
whereas normal SKI combinator calculus would be like this:
https://imgur.com/10pMxzC
(and all the inputs have the same label “x”)
So if the limitation of this is, that I can’t just forget about resources (similar, given my current understanding, to what some linear type system would actually be designed to do), then that certainly is a limitation, but, for many usecases, a useful one.
(Note, I do forget some resources though: In particular, once the diagram is reduced, or equivalently, the program is run, there is no way to tell how many combinators I started with to get to this behavior. I effectively only keep close track of unknown/variable inputs. Because Globular requires me to do so.)
I was in a bit of a rush in my previous comment.
Two addenda:
My very last remark was about not preserving all resources.
I’m pretty sure that’s nonsense in that resource aware type system would do exactly this: Count how often each variable is used. The combinators aren’t variables. So they can be safely forgotten about.
And secondly, I also wanted to clarify what I meant by these constraints “preserving composition”:
Take any non-reduced (but reducible, i.e. it shouldn’t be an infinite loop) small subsection Q of any given (reducible) program P and look at it separately. It will be a valid program on its own.
Now, reduce Q, turning it into Q_r.
Put Q_r back into the hole you cut into P, keeping all the wires in the same order. (Globular will also enforce the wiring order), obtaining a new program P’.
Reducing P will yield P_r.
Reducing P’ will yield P’_r.
My claim is, that (once again, being careful with infinite loops and such), P_r = P’_r.
At least in behavior. (I believe that means they are eta-equivalent?)
Different execution order may yield different exact layouts.
Some of that ought to be fixable as well, but I’m not sure all is:
I did not, as yet, add certain evidently true restructuring rules to Copy: Since it simply copies an input, arbitrary trees of copy hanging at the same input will give the exact same outcomes. Only the number of Copies is important.
So Commutativity and Associativity will hold for them.
Adding these would be quite trivial. Maybe I’ll make another update later just to get those relations as well.
I’m not sure adding just those laws would be enough to make the above claim even stronger, saying they even are exactly the same (in that shuffling around the way Copies are branched may transform one into the other).
That might well be the case though.
At any rate, my real point is that, if you keep this information around, you can plug in input-side the same stuff before and after reduction, and ultimately the behavior will be unchanged.
By deleting this information (especially the Eats which normally just disappear entirely), this could no longer be guaranteed. A reduced program would have a different number of inputs from an unreduced one, so you’d need to plug in different programs to begin with. Composition of programs would no longer necessarily even type-check, and if it did, behaviors wouldn’t have to be the same either, because, effectively, the wrong wires end up with the wrong inputs.
All this concerns vertical composition. I think there are no problems at all with horizontal composition which simply corresponds to tensoring together two programs to obtain a new program with the combined inputs and outputs side by side.
Right now I just have time for the easiest of your questions:
Half the time I use HTML:
<a href = "http://math.ucr.edu/home/baez/">my home page</a>and half the time I used Markdown, in the following manner:
[my home page](http://math.ucr.edu/home/baez/)You should be able to find one starting from here since I’m using some sort of default version of Markdown provided by WordPress for its blogs. But I don’t know what it is. I don’t do anything fancy, so it seems like everything I try to do with Markdown works on this blog, the Azimuth Forum (which runs on forum software called “Vanilla”) and also the n-Category Café (which runs on software called “Moveable Type”, together with a lot of homebrewed extra features by Jacques Distler).
You’re welcome to try stuff and see if it works; I don’t mind spending 5 minutes a day fixing formatting problems and discussing them!
Ok thanks. I see, I could include pictures too. That would have been a big improvement to many of the above comments. Oh well…