John D. Cook, Greg Egan, Dan Piponi and I had a fun mathematical adventure on Twitter. It started when John Cook wrote a program to compute the probability distribution of distances where
and
were two randomly chosen unit quaternions:
• John D. Cook, How far is xy from yx on average for quaternions?, 5 July 2018.
Three things to note before we move on:
• Click the pictures to see the source and get more information—I made none of them!
• We’ll be ‘randomly choosing’ lots of points on spheres of various dimensions. Whenever we do this, I mean that they’re chosen independently, and uniformly with respect to the unique rotation-invariant Borel measure that’s a probability measure on the sphere. In other words: nothing sneaky, just the most obvious symmetrical thing!
• We’ll be talking about lots of distances between points on the unit sphere in dimensions. Whenever we do this, I mean the Euclidean distance in
, not the length of the shortest path on the sphere connecting them.
Okay:
If you look at the histogram above, you’ll see the length is between 0 and 2. That’s good, since
and
are on the unit sphere in 4 dimensions. More interestingly, the mean looks bigger than 1. John Cook estimated it at 1.13.
Greg Egan went ahead and found that the mean is exactly
He did this by working out a formula for the probability distribution:
All this is great, but it made me wonder how surprised I should be. What’s the average distance between two points on the unit sphere in 4 dimensions, anyway?
Greg Egan worked this out too:
So, the mean distance for two randomly chosen unit quaternions is
The mean of is smaller than this. In retrospect this makes sense, since I know what quaternionic commutators are like: for example the points
at the ‘north and south poles’ of the unit sphere commute with everybody. However, we can now say the mean of
is exactly
times the mean of and there’s no way I could have guessed that.
While trying to get a better intuition for this, I realized that as you go to higher and higher dimensions, and you standing at the north pole of the unit sphere, the chance that a randomly chosen other point is quite near the equator gets higher and higher! That’s how high dimensions work. So, the mean value of should get closer and closer to
And indeed, Greg showed that this is true:
The graphs here show the probability distributions of distances for randomly chosen pairs of points on spheres of various dimensions. As the dimension increases, the probability distribution gets more sharply peaked, and the mean gets closer to
Greg wrote:
Here’s the general formula for the distribution, with plots for n=2,…,10. The mean distance does tend to √2, and the mean of the squared distance is always exactly 2, so the variance tends to zero.
But now comes the surprising part.
Dan Piponi looked at the probability distribution of distances in the 4-dimensional case:
and somehow noticed that its moments
when n is even, are the Catalan numbers!
Now if you don’t know about moments of probability distributions you should go read about those, because they’re about a thousand times more important than anything you’ll learn here.
And if you don’t know about Catalan numbers, you should go read about those, because they’re about a thousand times more fun than anything you’ll learn here.
So, I’ll assume you know about those. How did Dan Piponi notice that the Catalan numbers
were the even moments of this probability distribution? Maybe it’s because he recently managed to get ahold of Richard Stanley’s book on Amazon for just $11 instead of its normal price of $77.
(I don’t know how that happened. Some people write 7’s that look like 1’s, but….)
Anyway, you’ll notice that this strange phenomenon is all about points on the unit sphere in 4 dimensions. It doesn’t seem to involve quaternions anymore! So I asked if something similar happens in other dimensions, maybe giving us other interesting sequences of integers.
Greg Egan figured it out, and got some striking results:
Here d is the dimension of the Euclidean space containing our unit sphere, and Egan is tabulating the nth moment of the probability distribution of distances between two randomly chosen points on that sphere. The gnarly formula on top is a general expression for this moment in terms of the gamma function.
The obvious interesting feature of this table is that only for d = 2 and d = 4 rows are all the entries integers.
But Dan made another great observation: Greg left out the rather trivial d = 1 row, and that all the entries of this row would be integers too! Even better, d = 1, 2, and 4 are the dimensions of the associative normed division algebras: the real numbers, the complex numbers and the quaternions!
This made me eager to find a proof that all the even moments of the probability distribution of distances between points on the unit sphere in are integers when
is an associative normed division algebra.
The first step is to notice the significance of even moments.
First, we don’t need to choose both points on the sphere randomly: we can fix one and let the other vary. So, we can think of the distance
as a function on the sphere, or more generally a function of And when we do this we instantly notice that the square root is rather obnoxious, but all the even powers of the function
are polynomials on
Then, we notice that restricting polynomials from Euclidean space to the sphere is how we get spherical harmonics, so this problem is connected to spherical harmonics and ‘harmonic analysis’. The nth moment of the probability distribution of distances between points on the unit sphere in is
where we are integrating with respect to the rotation-invariant probability measure on the sphere. We can rewrite this as an inner product in namely
where 1 is the constant function equal to 1 on the whole sphere.
We’re looking at the even moments, so let n = 2m. Now, why should
be an integer when d = 1, 2 and 4? Well, these are the cases where the sphere is a group! For d = 1,
is the multiplicative group of unit real numbers, For d = 2,
is the multiplicative group of unit complex numbers. And for d = 4,
is the multiplicative group of unit quaternions.
These are compact Lie groups, and of a compact Lie group is very nice. Any finite-dimensional representation
of a compact Lie group
gives a function
called its character, given by
And it’s well-known that for two representations and
the inner product
is an integer! In fact it’s a natural number: just the dimension of the space of intertwining operators from to
So, we should try to prove that
is an integer this way. The function 1 is the character of the trivial 1-dimensional representation, so we’re okay there. What about
Well, there’s a way to take the mth tensor power of a representation
: you just tensor the representation with itself
times. And then you can easily show
So, if we can show is the character of a representation, we’re done:
will be one as well, and the inner product
will be an integer! Great plan!
Unfortunately, is not the character of a representation.
![]()
Unless is the completely silly 0-dimensional representation we have
where is the identity element of
But suppose we let
be the distance of
from the identity element—the natural choice of ‘north pole’ when we make our sphere into a group. Then we have
So can’t be a character. (It’s definitely not the character of the completely silly 0-dimensional representation: that’s zero.)
But there’s a well-known workaround. We can work with virtual representations, which are formal differences of representations, like this:
The character of a virtual representation is defined in the obvious way
Since the inner product of characters of two representations is a natural number, the inner product of characters of two virtual representations will be an integer. And we’ll be completely satisfied if we prove that
is an integer, since it’s obviously ≥ 0.
So, we just need to show that is the character of a virtual representation. This will easily follow if we can show
itself is the character of a virtual representation: you can tensor virtual representations, and then their characters multiply.
So, let’s do it! I’ll just do the quaternionic case. I’m doing it right now, thinking out loud here. I figure I should start with a really easy representation, take its character, compare that to our function and then fix it by subtracting something.
Let be the spin-1/2 representation of
which just sends every matrix in
to itself. Every matrix in
is conjugate to one of the form
so we can just look at those, and we have
On the other hand, we can think of as a unit quaternion, and then
where now stands for the quaternion of that name! So, its distance from 1 is
and if we square this we get
So, we’re pretty close:
In particular, this means is the character of the virtual representation
where is the 1d trivial rep and
is the spin-1/2 rep.
So we’re done! ![]()
At least we’re done showing the even moments of the distance between two randomly chosen points on the 3-sphere is an integer. The 1-sphere and 0-sphere cases are similar.
But course there’s another approach! We can just calculate the darn moments and see what we get. This leads to deeper puzzles, which we have not completely solved. But I’ll talk about these next time, in Part 2.








You accidentally used the same graph twice.
Whoops, thanks – I’ll fix that. The two graphs look very similar when they’re near-microscopic icons on my desktop.
What a joy it is to read and try to work through this.
TWF improved my (amateur, bystander) life for years stretching far back in the jurassic ages, too.
Thanks so much for so much shared sustained enthusiasm and insight, John et al.
I’m glad you liked it! I’ve been called a “protoblogger”, which always made me think of Pithecanthropus or Australopithecus learning to make primitive stone tools—but now it seems the Jurassic is a more apt metaphor.
I know, you didn’t mean it negatively! It’s just funny—it reminds me of Gian-Carlo’s advice:
I had the pleasure of taking baby, elementary classes from Rota (and Stanley, and Mike Artin, and Kan, Quillen, Munkres, Dudley, Mattuck, Melrose, Vogan, …) back in the day. What a pleasure at the time, and what a squandering of opportunity in retrospect. Youth is indeed wasted on the young, or at least on the the burned-out-gave-up-too-early.
Seriously, your blogging is a service to the (dying: rage, rage against) world.
Gian-Carlo Rota said:
I think it is most often rather the position in an institution and the function of being a representative of that institution, which makes you look like being an institution (if you are old). That is for example if you are getting old in showbiz then you better sooner than later marry a boss of an oil company – there are very few people who happily survive in showbiz in old age. Like even Marlene Dietrich hid herself in her Paris apartment in the last years of her life and refused to be filmed in order to stay “an institution”.
I noticed the Catalan number connection because of the similarity to the PDF for eigenvalues of certain random matrices – the Wigner semi-circle distribution. (I guess you saw the random matrix animations I was doing.) I knew that had Catalan number moments. I’ve been wondering if there’s a random matrix connection somewhere here.
BTW I just found the “Wigner n-sphere distribution” at wikipedia in the Wigner semi-circle article: https://en.wikipedia.org/wiki/Wigner_semicircle_distribution
[…] Random Points on a Sphere (Part 1) 2 by johndcook | 0 comments on Hacker News. […]
[…] Random Points on a Sphere (Part 1) 4 by johndcook | 0 comments on Hacker News. […]
I realized that it’s not hard, in principle, to actually compute the even moments in the d = 4 case using my formula for them:
and a bit of SU(2) representation theory.
Remember that SU(2) has irreducible representations of spin
Let’s call these
The rules for tensoring them are well-known; in particular
and
where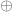 means ‘direct sum’. However, I want to identify representations with their character, so I can subtract as well as add them—or in other words, I want to work with virtual representations. So I’ll just write
means ‘direct sum’. However, I want to identify representations with their character, so I can subtract as well as add them—or in other words, I want to work with virtual representations. So I’ll just write  and
and  instead of
instead of 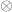 and
and 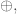 and in this language I showed
and in this language I showed
so we get formulas like
and so on.
In the current language, our formula for the even moments is
and it’s a fact of group representation theory that this just counts the number of times the trivial representation![[0]](https://s0.wp.com/latex.php?latex=%5B0%5D&bg=ffffff&fg=333333&s=0&c=20201002) shows up in
shows up in 
So, for example, the fourth moment is
just as we expect.
With more work one should be able to show using this method that
namely the (m+1)st Catalan number. And I feel suspect it will boil down to how the Catalan numbers count ‘mountain ranges’ like this:
Here’s something simpler that’s related: the number of times the trivial representation shows up in the (2m)th tensor power of the spin-1/2 representation is the Catalan number
Maybe someone has the energy to push this forward! It’s just combinatorics now.
Very nice!
I think there is a small mistake in the last line of your calculation of ; it should be:
; it should be:
I suspect you could prove the result by induction, but it would probably require a simultaneous proof of a general formula for the coefficients of all the irreps, not just [0], because each multiplication by 2[0]-[1/2] produces irreps of lower spin that eventually come back to [0], so we can’t ignore all the higher-spin irreps that arise along the way.
I get the following coefficients for the virtual irreps [0], [1/2], … [5] in the first 10 powers of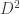 :
:
The OEIS recognises the absolute value of the second column as “the fourth convolution of the Catalan numbers,” 4*binomial(2n+3,n)/(n+4), and some of the other columns. But I hope I’m wrong about needing to track all the higher-spin irreps, and there’s actually some clever short-cut that just takes you straight to the coefficient of [0].
Ah, if you start with the diagonal (2,–4,6,…) and then take descending parallel slices through the matrix, the formulas for the absolute values of these coefficients, in terms of an integer column number starting at 1, are:
That’s a bit less daunting.
It looks like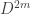 is:
is:
That’s true for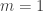 , and the coefficient of [0] is
, and the coefficient of [0] is 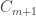 , so if we can prove the induction on
, so if we can prove the induction on  , we’re done.
, we’re done.
I’ve convinced myself that the formula above is true, but I’m too lazy to write out the induction on . And by this point, what I’ve done here is probably at least as much work as doing the integral explicitly, so I’ll call it quits.
. And by this point, what I’ve done here is probably at least as much work as doing the integral explicitly, so I’ll call it quits.
Maybe someone else can see an easier route to getting the coefficients of [0], but in any case, at least the representation-theoretic approach does explain the integral values of the moments for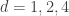 .
.
I’m hoping there’s an easier route.
After all, suppose someone asked us to compute the dimension of the trivial subspace of the rep [1/2]⊗n. We might think it necessary to compute the dimension of the spin-j subspace of [1/2]⊗n for all n,j since after all the spin can ‘climb up’ a bunch as we repeatedly tensor by [1/2] before it ‘climbs back down’.
However, we can also realize that we’re trying to count mountain ranges of length 2n that start at 0 and either climb up or down by 1/2 at each step, getting back down to 0 at the (2n)th step and never sinking below sea level. So the answer is the Catalan number Cn.
The problem is that now we’re counting things with signs: I guess we’re counting mountain ranges of length 2n where at each step we can go up one, down one, or stay level—but we include a factor of -1 when we go up or down, and 2 when we stay level. For some reason this gives Catalan numbers too!
Maybe the way to tackle this is to say, at each step, that if we stay level we can excise that step and get a shorter mountain range. Then we’d need to show that each Catalan number Cn is a certain weighted sum of Catalan numbers Ck for k ≤ n.
The Catalan Clan is also associated with parenthesized words and through them with the counting of diagrams in a Temperley-Lieb algebra, but what are they “counting” in this case if anything?
Great question! It pays to stop and think about what one is doing, now and then.
The (2m)th moment of the probability distribution of distances for two unit quaternions is the same as the the dimension of the SU(2)-invariant part of the mth tensor power of the virtual representation![2[0] - [\frac{1}{2}]](https://s0.wp.com/latex.php?latex=2%5B0%5D+-+%5B%5Cfrac%7B1%7D%7B2%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) , which is the (m+1)st Catalan number.
, which is the (m+1)st Catalan number.
Since this representation is a virtual representation, a formal difference of representations, we have to interpret the word ‘dimension’ in a similar virtual sense: I really mean a difference of dimensions.
The dimension of invariant part of the actual representation![[\frac{1}{2}]^{\otimes n}](https://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B1%7D%7B2%7D%5D%5E%7B%5Cotimes+n%7D&bg=ffffff&fg=333333&s=0&c=20201002) can be computed combinatorially in various ways, e.g. by counting certain diagrams called spin networks. We get Catalan numbers this way.
can be computed combinatorially in various ways, e.g. by counting certain diagrams called spin networks. We get Catalan numbers this way.
Here however we are counting diagrams with signs.
I can see two natural generalisations here.
There is a higher dimensional analogue of the commutator question. If you write then one can think of
then one can think of  as point on
as point on 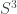 and
and  as an element of Spin(4) acting on
as an element of Spin(4) acting on 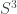 . Actually since
. Actually since  acts trivially we may as well consider the action of SO(4). Thus the higher dimensional analogue is the distribution and expected values (aka moments) of
acts trivially we may as well consider the action of SO(4). Thus the higher dimensional analogue is the distribution and expected values (aka moments) of 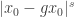 for a fixed point
for a fixed point 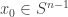 and
and  uniform on SO(n).
uniform on SO(n).
It is equally natural to consider the distribution and expected values of the distances measured with geodesic distance on the sphere, rather than the Euclidean distance. Using stereoscopic projection this is just the distribution of times a Jacobian depending on r and n .
times a Jacobian depending on r and n .
Ouch.
The first point is the wrong analogy. In the first case the unit quaternions (i.e. Sp(1)) act by conjugation so on the direct sum of the trivial and the adjoint representation. Hence the analogue would be in full generality, for a (reducible of irreducible representation) V of compact group with an invariant metric, consider a vector
with an invariant metric, consider a vector  in the sphere and consider the distribution and expectation (aka moments) of
in the sphere and consider the distribution and expectation (aka moments) of  or
or  where
where  is the geodesic distance on the sphere
is the geodesic distance on the sphere  .
.
If the sphere is homogeneous space for the action (i.e.
action (i.e.  acts fixpoint-free) then the Haar measure is pushed forward to the uniform measure on the sphere on the sphere, and the distribution
acts fixpoint-free) then the Haar measure is pushed forward to the uniform measure on the sphere on the sphere, and the distribution  is just the distribution of
is just the distribution of 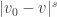 for
for  .
.
I am not a mathematician, but I was able to follow a lot of this due to your good written communication skills and the sequential process of bringing the reader along. This topic of doing math on higher dimensions is beyond fascinating to me. Do you know of a solid or even seminal book on this topic?
Do you know about linear algebra, inner product spaces and the like? If not, that would be the place to start, and I recommend this free book:
• Jim Hefferon, Linear Algebra, available free online at http://joshua.smcvt.edu/linalg.html/.
If you already know this material and want to go further, there are many directions to go—so many, in fact, that it’s hard for me to make a recommendation unless you narrow things down a bit!
If I’ve done my integrals correctly, we have that in the average distance from
the average distance from  to
to  for a randomly chosen unit
for a randomly chosen unit  is
is  , which is also the average distance between two randomly chosen unit complexes.
, which is also the average distance between two randomly chosen unit complexes.
I wonder what the average distance is between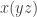 and
and  in the octonions is.
in the octonions is.
Oscar wrote:
If you’d asked this question more than two days ago I couldn’t have told you, but now I can!
The average distance between and
and  for randomly chosen unit octonions is 1.095, and here is a histogram of the distribution:
for randomly chosen unit octonions is 1.095, and here is a histogram of the distribution:
Thank John Cook for this:
• John D. Cook, How close is octonion multiplication to being associative?, 9 July 2018.
Of course, his estimate of the average noncommutativity of the quaternions is what started the ball rolling here.
Some late-breaking news: Greg Egan has exactly computed the average value of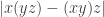 for unit octonions: it’s
for unit octonions: it’s
At some point in one’s experience one drops the exclamation point from “it turns out to be a power of 2!”, later from “it turns out to be a binomial coefficients!”, and I may be ready to lose it from “it turns out to be a Catalan number!”.
I’m really intrigued by that 5/6 factor, though, which would be a reasonable thing to measure for any compact group G + unitary representation V. As you say, for measuring the average distance x to y we may as well assume x is 1, but in addition, we may as well assume y is in the torus or even the Weyl alcove (an interval, in your G = U(1,H) example), which we then weight by the volume of the conjugacy class (independent of V). For measuring the distance between commutators, once again it’s reasonable to assume y in the Weyl alcove, but I don’t see much simplification available on x.
Allen wrote:
On the other hand, factorials never lose their power to thrill.
That sounds fun. We thought we were studying spheres—and in Part 2 we actually will—but there’s probably a lot more fun to be had studying compact groups with unitary representations! We actually looked a couple of questions that could generalize to those.
[…] Last time I showed that if you randomly choose two points on the unit sphere in 1-, 2- or 4-dimensional space and look at the probability distribution of their distances, then the even moments of this probability distribution are always integers. To do this, I used some group representation theory. […]
Does the appearance of the virtual character![2[0]-[1/2]](https://s0.wp.com/latex.php?latex=2%5B0%5D-%5B1%2F2%5D&bg=ffffff&fg=333333&s=0&c=20201002) have an interpretation along the lines of those in the answers of this old MO question by ARupinski?
have an interpretation along the lines of those in the answers of this old MO question by ARupinski?
André Henriques’ answer (hey! I know him!) gives a nice list of ways of thinking about virtual vector spaces, starting from the simplest, which I used in my post: namely, they’re just formal differences of vector spaces like V – W. The problem with that answer is that it doesn’t say what maps between virtual vector spaces are. So it doesn’t really let us think of virtual vector spaces as objects in a mathematical sense: that is, things having maps between them.
Ultimately all this is part of the age-old puzzle: “what are negative numbers, really?” Or, in more concrete terms, “I know what it’s like to have 2 apples; what’s it like to have -2 apples?” And of course many answers are known, but the most popular ones don’t say what it means to peel -2 apples.
I have worked on this stuff:
• John Baez, The mysteries of counting, 14 July 2005.
I don’t yet see a use for the more high-brow approaches to virtual representations in our puzzles here. However, I would like to generalize our puzzles from “spheres in Euclidean space that happen to be groups” to “groups that happen to live in Euclidean space”… and if we do that, we may ultimately see some advantages of a high-brow approach. I don’t know.
I want to point out a tantalizing analogy that might be clarified by thinking of
and
as special cases compact Lie groups equipped with a faithful unitary representation.
If we have a compact Lie group with a faithful unitary representation on
with a faithful unitary representation on 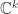 , we can say
, we can say
that is, it sits inside the algebra of matrices, which has a nice Euclidean distance function on it:
matrices, which has a nice Euclidean distance function on it:
Moreover has a unique translation-invariant probability measure on that’s a Borel measure, called ‘normalized Haar measure’.
has a unique translation-invariant probability measure on that’s a Borel measure, called ‘normalized Haar measure’.
So, the distance from the identity element is a function on and we can try to compute its mean, variance, and higher moments.
and we can try to compute its mean, variance, and higher moments.
And I believe if we normalize things correctly (which I may have just done), we will often get sequences of integers this way.
It would be nice to understand these. I think the first informative new case would be , with its usual representation on
, with its usual representation on 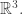 (I was using complex representations, but in this case working
(I was using complex representations, but in this case working 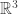 gives the same answer as if we’d used
gives the same answer as if we’d used 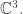 )
)
However, before even trying this, I got sidetracked by some pleasant thought about the two cases we already did!
The distance function on
has even moments that are central binomial coefficients, while the distance function
has even moments that are Catalan numbers.
Thinking about these two cases suggests some clues that may help us figure out the general pattern.
The irreducible representations of are indexed by integers. Imagine doing a discrete-time random walk on the integers, starting at 0, where at each time you take one step either left or right. How many ways are there to get back to 0 after
are indexed by integers. Imagine doing a discrete-time random walk on the integers, starting at 0, where at each time you take one step either left or right. How many ways are there to get back to 0 after 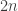 steps?
steps?
So we’re getting central binomial coefficients.
The irreducible representations of are indexed by nonnegative integers (twice the physicists ‘spins’). Imagine doing a discrete-time random walk on the nonnegative integers, starting at 0, where at each time you take one step either left or right. How many ways are there to get back to 0 after
are indexed by nonnegative integers (twice the physicists ‘spins’). Imagine doing a discrete-time random walk on the nonnegative integers, starting at 0, where at each time you take one step either left or right. How many ways are there to get back to 0 after 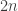 steps?
steps?
So we’re getting Catalan numbers!
In short, the even moments of the distance function for seem to be counting walks from the trivial representation to itself in the set of irreducible representations of
seem to be counting walks from the trivial representation to itself in the set of irreducible representations of 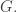
There’s something about this that’s obvious from my post… but there’s also something nonobvious! The nonobvious part is that the square of the distance function is the character of a virtual representation; tensoring with this virtual representation over and over again generates a kind of random walk on the set of irreducible representation, but it’s not the ‘obvious’ random walk I just described!
You’ll see this from how hard Greg worked to show that the even moments for
are Catalan numbers.
So, there’s something sneaky going on, which I don’t understand. But we can still go ahead and try to figure out the even moments of the distance function for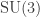 , which will be related to a random walk in the set of irreducible representations for
, which will be related to a random walk in the set of irreducible representations for 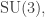 the
the 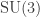 Weyl chamber, which looks like 1/6th of a triangular lattice.
Weyl chamber, which looks like 1/6th of a triangular lattice.
(Or, for a less thrilling but probably instructive example, .)
.)
In Random Points on a Sphere (Part 1), we learned an interesting fact. You can take the unit sphere in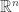 , randomly choose two points on it, and compute their distance. This gives a random variable, whose moments you can calculate.
, randomly choose two points on it, and compute their distance. This gives a random variable, whose moments you can calculate.
And then for the interesting part: when n = 1, 2 or 4, and seemingly in no other cases, all the even moments are integers.
The reason is that these are the dimensions in which the spheres are groups. We can see that the even moments are integers because they are differences of dimensions of certain representations of these groups. So, Rogier Brussee and Allen Knutson pointed out that if we want to broaden our line of investigation, we can look at other compact Lie groups. That’s what I’ll do today.
I opened a Twitter account back in March 2016 but had not been active at all without even a single tweeting until this May 2018 simply because I thought it would be just wasting my time. I was so wrong about that and I wish I started using Twitter much earlier. Here is what I found. Twitter can be a great social media platform for intellectual activities including getting and sharing information, discussing ideas and opinions on math and getting connected with people in the disciplines of your interests in math. I also recently witnessed an amazing collaborative math work being done on Twitter and that makes me think that Twitter can be also an effective research tool for mathematicians to collaborate with other mathematicians. I was also pleasantly surprised that there are quite a few mathematicians who are tweeting actively and daily tweets from some of them are quite intellectually stimulating. I particularly love inspirational and informative tweets from John Baez and Sam Walters. Reading their tweets and participating in the discussions whenever I can became a great joy of my daily life.
I’m not sure if I’ll ever have the energy to rigorously prove the following formula, but based on some proofs of particular subsets and a lot of empirical evidence for the rest, I’m 99% sure that the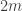 th moment of the volume of a
th moment of the volume of a  -simplex whose vertices are chosen at random from a unit sphere in
-simplex whose vertices are chosen at random from a unit sphere in  is given by:
is given by:
If that’s a bit much to digest, the first even moment, the mean of the squared volume of the -simplex, is:
-simplex, is:
For any given the formula can be expressed in terms of gamma functions, and the odd moments, such as the mean volume, can then be found by setting
the formula can be expressed in terms of gamma functions, and the odd moments, such as the mean volume, can then be found by setting  to half-integer values.
to half-integer values.
This is great! I’m amazed that such a simple formula exists. Not that it’s so simple—but it’s still simpler than I would have guessed!
Over on Twitter I conjectured a formula for the mean volume of a -simplex in the unit sphere in
-simplex in the unit sphere in 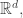 in the limit
in the limit  I’m guessing it should equal the volume of a regular
I’m guessing it should equal the volume of a regular  -simplex whose sides have length
-simplex whose sides have length 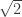 .
.
But I would be perfectly content to know that the variance of the volume of a -simplex in the unit sphere in
-simplex in the unit sphere in 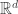 approaches the square of the volume of a regular
approaches the square of the volume of a regular  -simplex whose sides have length
-simplex whose sides have length 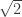 .
.
I think you mean the second moment, not the variance! The variance approaches zero. But the second moment certainly does approach the squared volume of the regular -simplex whose edges have length
-simplex whose edges have length 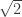 , which is:
, which is:
Great! Yes, I meant the second moment. I must be going senile, because at the time I was sure that ‘variance’ was a shorthand for ‘second moment’ just like ‘mean’ is short for ‘first moment’.
It’s cool that the squared volume of a regular -simplex with sides of length
-simplex with sides of length 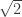 looks simpler than the volume of a regular
looks simpler than the volume of a regular  -simplex with sides of length 1… mainly because of the
-simplex with sides of length 1… mainly because of the 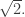 I guess it means that the nicest regular
I guess it means that the nicest regular 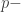 simplex is the one in
simplex is the one in 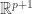 whose corners are
whose corners are
I see: there’s a really quick mental way to compute the volume of that particular -simplex.
-simplex.
I know how to get the squared volume from the determinant of a Gramian matrix that is 2 on the diagonal and 1 elsewhere, but you must have a better trick!
I think I’ve guessed your trick for computing the volume of that -simplex. You know that the volume of the
-simplex. You know that the volume of the 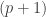 -simplex with the same vertices plus the origin in
-simplex with the same vertices plus the origin in 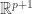 is
is 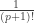 , and its “height” is easily seen to be
, and its “height” is easily seen to be  . So:
. So:
I still like the Gram matrix version, too! I get more confused trying to juggle ratios with factorials and square roots in my head than I do picturing a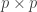 matrix with integer entries: first all 1s except 2 on the diagonal, then all
matrix with integer entries: first all 1s except 2 on the diagonal, then all  along the first row, and then the same as the identity matrix for other rows … so the determinant is just
along the first row, and then the same as the identity matrix for other rows … so the determinant is just  .
.
Yes, that’s my trick. Sorry for not writing it up sooner!
I always found the volume of a regular tetrahedron a bit annoying, so I’m happy that putting it in one extra dimension makes it easier to understand. I’m especially happy that it’s connected to the nice description of the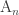 lattice:
lattice: