I’ve been spending the last month at the Centre of Quantum Technologies, getting lots of work done. This Friday I’m giving a talk, and you can see the slides now:
• John Baez, Getting to the bottom of Noether’s theorem.
Abstract. In her paper of 1918, Noether’s theorem relating symmetries and conserved quantities was formulated in term of Lagrangian mechanics. But if we want to make the essence of this relation seem as self-evident as possible, we can turn to a formulation in term of Poisson brackets, which generalizes easily to quantum mechanics using commutators. This approach also gives a version of Noether’s theorem for Markov processes. The key question then becomes: when, and why, do observables generate one-parameter groups of transformations? This question sheds light on why complex numbers show up in quantum mechanics.
At 5:30 on Saturday October 6th I’ll talk about this stuff at this workshop in London:
• The Philosophy and Physics of Noether’s Theorems, 5-6 October 2018, Fischer Hall, 1-4 Suffolk Street, London, UK. Organized by Bryan W. Roberts (LSE) and Nicholas Teh (Notre Dame).
This workshop celebrates the 100th anniversary of Noether’s famous paper connecting symmetries to conserved quantities. Her paper actually contains two big theorems. My talk is only about the more famous one, Noether’s first theorem, and I’ll change my talk title to make that clear when I go to London, to avoid getting flak from experts. Her second theorem explains why it’s hard to define energy in general relativity! This is one reason Einstein admired Noether so much.
I’ll also give this talk at DAMTP—the Department of Applied Mathematics and Theoretical Physics, in Cambridge—on Thursday October 4th at 1 pm.
The organizers of London workshop on the philosophy and physics of Noether’s theorems have asked me to write a paper, so my talk can be seen as the first step toward that. My talk doesn’t contain any hard theorems, but the main point—that the complex numbers arise naturally from wanting a correspondence between observables and symmetry generators—can be expressed in some theorems, which I hope to explain in my paper.
Azimuth 
Which of her theorems?
Hi! I explained in the article: the one called Noether’s first theorem, which obtains conserved quantities from symmetries of a Lagrangian. (Click the link for details.)
Nice, thanks for sharing.
Dear Professor Baez, there is an “o” missing, in the word “topology”, in the quotation of H. Weyl. Thank you so much for sharing.
J.
Thanks! I’ll fix that.
Too early in the morning I posted a comment which was wrong. I guess it has failed or will fail moderation. Which is good. Cheers.
Actually now that I have logged in again I can see it. But I can’t see how to delete it.
You can’t delete comments here—only I can. I’ve deleted it, since that’s apparently what you want.
I really enjoyed reading those slides! It only took about 15 minutes, but it was incredibly clear and enlightening.
Great – thanks! That means a lot, since you’re the kind of person I’d like to communicate to, and I was worrying this presentation was too algebraic to really resonate with most such people—hence my self-deprecatory joke about the devil of algebra.
John,
Very interesting. Can you post your talk or a summary? I follow you on G+, we would welcome a post like this in our G+community, Advanced Thermodynamics.
I did post my talk slides—that’s what this blog article was about.
The slides are very clear and quite interesting. They encourage me to try and work through your paper, when it comes out. Could you comment on how this relates to time-reversibility in the laws of classical mechanics? And what happens in complex vs. real and quaternionic quantum mechanics? I am hoping to gain insight into information flow in biological systems, where history intrudes in irreversible ways.
I’m glad you liked my paper. I’m not sure how any of this relates to time-reversibility in the laws of classical mechanics—do you have anything specific in mind? Note that in the formalisms I’m describing, every observable
generates a one-parameter group of symmetries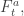 
defined for all 
both positive and negative. In particular
so all these transformations are invertible.
That’s a long story. I wrote a paper about it:
• John Baez, Division algebras and quantum theory, Found. Phys. 42 (2012), 819–855.
arguing that real, complex and quaternionic quantum mechanics are all part of unified structure that is actually already being used in physics without people paying much attention to it.
My new paper will use Noether’s theorem ideas to explain why the complex numbers are ‘the first among equals’ in the trinity of associative normed division algebras.
John
Are the Noether conference papers going to be put online for anyone to read?
Peter
The organizers have collected the participants’ slides and I hope these will be made public. Videos have been made of the participants’ talks, and I hope and believe these will be made public. Furthermore, there will eventually be a conference proceedings volume.
When something shows up, I’ll let everyone know about it on this blog.