Here is a conversation I had with Scott Aaronson. It started on his blog, in a discussion about ‘fine-tuning’. Some say the Standard Model of particle physics can’t be the whole story, because in this theory you need to fine-tune the fundamental constants to keep the Higgs mass from becoming huge. Others say this argument is invalid.
I tried to push the conversation toward the calculations actually underlie this argument. Then our conversation drifted into email and got more technical… and perhaps also more interesting, because it led us to contemplate the stability of the vacuum!
You see, if we screwed up royally on our fine-tuning and came up with a theory where the square of the Higgs mass was negative, the vacuum would be unstable. It would instantly decay into a vast explosion of Higgs bosons.
Another possibility, also weird, turns out to be slightly more plausible. This is that the Higgs mass is positive—as it clearly is—and yet the vacuum is ‘metastable’. In this scenario, the vacuum we see around us might last a long time, and yet eventually it could decay through quantum tunnelling to the ‘true’ vacuum, with a lower energy density:
Little bubbles of true vacuum would form, randomly, and then grow very rapidly. This would be the end of life as we know it.
Scott agreed that other people might like to see our conversation. So here it is. I’ll fix a few mistakes, to make me seem smarter than I actually am.
I’ll start with some stuff on his blog.
If I said, “supersymmetry basically has to be there because it’s such a beautiful symmetry,” that would be an argument from beauty. But I didn’t say that, and I disagree with anyone who does say it. I made something weaker, what you might call an argument from the explanatory coherence of the world. It merely says that, when we find basic parameters of nature to be precariously balanced against each other, to one part in 1010 or whatever, there’s almost certainly some explanation. It doesn’t say the explanation will be beautiful, it doesn’t say it will be discoverable by an FCC or any other collider, and it doesn’t say it will have a form (like SUSY) that anyone has thought of yet.
Scott wrote:
It merely says that, when we find basic parameters of nature to be precariously balanced against each other, to one part in 1010 or whatever, there’s almost certainly some explanation.
Do you know examples of this sort of situation in particle physics, or is this just a hypothetical situation?
To answer a question with a question, do you disagree that that’s the current situation with (for example) the Higgs mass, not to mention the vacuum energy, if one considers everything that could naïvely contribute? A lot of people told me it was, but maybe they lied or I misunderstood them.
The basic rough story is this. We measure the Higgs mass. We can assume that the Standard Model is good up to some energy near the Planck energy, after which it fizzles out for some unspecified reason.
According to the Standard Model, each of the 25 fundamental constants appearing in the Standard Model is a “running coupling constant”. That is, it’s not really a constant, but a function of energy: roughly the energy of the process we use to measure that process. Let’s call these “coupling constants measured at energy E”. Each of these 25 functions is determined by the value of all 25 functions at any fixed energy E – e.g. energy zero, or the Planck energy. This is called the “renormalization group flow”.
So, the Higgs mass we measure is actually the Higgs mass at some energy E quite low compared to the Planck energy.
And, it turns out that to get this measured value of the Higgs mass, the values of some fundamental constants measured at energies near the Planck mass need to almost cancel out. More precisely, some complicated function of them needs to almost but not quite obey some equation.
People summarize the story this way: to get the observed Higgs mass we need to “fine-tune” the fundamental constants’ values as measured near the Planck energy, if we assume the Standard Model is valid up to energies near the Planck energy.
A lot of particle physicists accept this reasoning and additionally assume that fine-tuning the values of fundamental constants as measured near the Planck energy is “bad”. They conclude that it would be “bad” for the Standard Model to be valid up to the Planck energy.
(In the previous paragraph you can replace “bad” with some other word—for example, “implausible”.)
Indeed you can use a refined version of the argument I’m sketching here to say “either the fundamental constants measured at energy E need to obey an identity up to precision ε or the Standard Model must break down before we reach energy E”, where ε gets smaller as E gets bigger.
Then, in theory, you can pick an ε and say “an ε smaller than that would make me very nervous.” Then you can conclude that “if the Standard Model is valid up to energy E, that will make me very nervous”.
(But I honestly don’t know anyone who has approximately computed ε as a function of E. Often people seem content to hand-wave.)
People like to argue about how small an ε should make us nervous, or even whether any value of ε should make us nervous.
But another assumption behind this whole line of reasoning is that the values of fundamental constants as measured at some energy near the Planck energy are “more important” than their values as measured near energy zero, so we should take near-cancellations of these high-energy values seriously—more seriously, I suppose, than near-cancellations at low energies.
Most particle physicists will defend this idea quite passionately. The philosophy seems to be that God designed high-energy physics and left his grad students to work out its consequences at low energies—so if you want to understand physics, you need to focus on high energies.
Scott wrote in email:
Do I remember correctly that it’s actually the square of the Higgs mass (or its value when probed at high energy?) that’s the sum of all these positive and negative high-energy contributions?
John wrote:
Sorry to take a while. I was trying to figure out if that’s a reasonable way to think of things. It’s true that the Higgs mass squared, not the Higgs mass, is what shows up in the Standard Model Lagrangian. This is how scalar fields work.
But I wouldn’t talk about a “sum of positive and negative high-energy contributions”. I’d rather think of all the coupling constants in the Standard Model—all 25 of them—obeying a coupled differential equation that says how they change as we change the energy scale. So, we’ve got a vector field on
that says how these coupling constants “flow” as we change the energy scale.
Here’s an equation from a paper that looks at a simplified model:
Here
is the Higgs mass,
is the mass of the top quark, and both are being treated as functions of a momentum
(essentially the energy scale we’ve been talking about).
is just a number. You’ll note this equation simplifies if we work with the Higgs mass squared, since
This is one of a bunch of equations—in principle 25—that say how all the coupling constants change. So, they all affect each other in a complicated way as we change
By the way, there’s a lot of discussion of whether the Higgs mass square goes negative at high energies in the Standard Model. Some calculations suggest it does; other people argue otherwise. If it does, this would generally be considered an inconsistency in the whole setup: particles with negative mass squared are tachyons!
I think one could make a lot of progress on these theoretical issues involving the Standard Model if people took them nearly as seriously as string theory or new colliders.
Scott wrote:
So OK, I was misled by the other things I read, and it’s more complicated than
being a sum of mostly-canceling contributions (I was pretty sure
Rather, there’s a coupled system of 25 nonlinear differential equations, which one could imagine initializing with the “”true”” high-energy SM parameters, and then solving to find the measured low-energy values. And these coupled differential equations have the property that, if we slightly changed the high-energy input parameters, that could generically have a wild effect on the low-energy outputs, pushing them up to the Planck scale or whatever.
Philosophically, I suppose this doesn’t much change things compared to the naive picture: the question is still, how OK are you with high-energy parameters that need to be precariously tuned to reproduce the low-energy SM, and does that state of affairs demand a new principle to explain it? But it does lead to a different intuition: namely, isn’t this sort of chaos just the generic behavior for nonlinear differential equations? If we fix a solution to such equations at a time
our solution will almost always appear “finely tuned” at a faraway time
—tuned to reproduce precisely the behavior at
that we fixed previously! Why shouldn’t we imagine that God fixed the values of the SM constants for the low-energy world, and they are what they are at high energies simply because that’s what you get when you RG-flow to there?
I confess I’d never heard the speculation that
John wrote:
Scott wrote:
Rather, there’s a coupled system of 25 nonlinear differential equations, which one could imagine initializing with the “”true”” high-energy SM parameters, and then solving to find the measured low-energy values. And these coupled differential equations have the property that, if we slightly changed the high-energy input parameters, that could generically have a wild effect on the low-energy outputs, pushing them up to the Planck scale or whatever.
Right.
Philosophically, I suppose this doesn’t much change things compared to the naive picture: the question is still, how OK are you with high-energy parameters that need to be precariously tuned to reproduce the low-energy SM, and does that state of affairs demand a new principle to explain it? But it does lead to a different intuition: namely, isn’t this sort of chaos just the generic behavior for nonlinear differential equations?
Yes it is, generically.
Physicists are especially interested in theories that have “ultraviolet fixed points”—by which they usually mean values of the parameters that are fixed under the renormalization group flow and attractive as we keep increasing the energy scale. The idea is that these theories seem likely to make sense at arbitrarily high energy scales. For example, pure Yang-Mills fields are believed to be “asymptotically free”—the coupling constant measuring the strength of the force goes to zero as the energy scale gets higher.
But attractive ultraviolet fixed points are going to be repulsive as we reverse the direction of the flow and see what happens as we lower the energy scale.
So what gives? Are all ultraviolet fixed points giving theories that require “fine-tuning” to get the parameters we observe at low energies? Is this bad?
Well, they’re not all the same. For theories considered nice, the parameters change logarithmically as we change the energy scale. This is considered to be a mild change. The Standard Model with Higgs may not have an ultraviolet fixed point, but people usually worry about something else: the Higgs mass changes quadratically with the energy scale. This is related to the square of the Higgs mass being the really important parameter… if we used that, I’d say linearly.
I think there’s a lot of mythology and intuitive reasoning surrounding this whole subject—probably the real experts could say a lot about it, but they are few, and a lot of people just repeat what they’ve been told, rather uncritically.
If we fix a solution to such equations at a time
This is something I can imagine Sabine Hossenfelder saying.
I confess I’d never heard the speculation that
The experts are still arguing about this; I don’t really know. To show how weird all this stuff is, there’s a review article from 2013 called “The top quark and Higgs boson masses and the stability of the electroweak vacuum”, which doesn’t look crackpotty to me, that argues that the vacuum state of the universe is stable if the Higgs mass and top quark are in the green region, but only metastable otherwise:
The big ellipse is where the parameters were expected to lie in 2012 when the paper was first written. The smaller ellipses only indicate the size of the uncertainty expected after later colliders made more progress. You shouldn’t take them too seriously: they could be centered in the stable region or the metastable region.
An appendix give an update, which looks like this:
The paper says:
one sees that the central value of the top mass lies almost exactly on the boundary between vacuum stability and metastability. The uncertainty on the top quark mass is nevertheless presently too large to clearly discriminate between these two possibilities.
Then John wrote:
By the way, another paper analyzing problems with the Standard Model says:
It has been shown that higher dimension operators may change the lifetime of the metastable vacuum,
, from
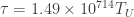
to
where
is the age of the Universe.
In other words, the calculations are not very reliable yet.
And then John wrote:
Sorry to keep spamming you, but since some of my last few comments didn’t make much sense, even to me, I did some more reading. It seems the best current conventional wisdom is this:
Assuming the Standard Model is valid up to the Planck energy, you can tune parameters near the Planck energy to get the observed parameters down here at low energies. So of course the the Higgs mass down here is positive.
But, due to higher-order effects, the potential for the Higgs field no longer looks like the classic “Mexican hat” described by a polynomial of degree 4:
with the observed Higgs field sitting at one of the global minima.
Instead, it’s described by a more complicated function, like a polynomial of degree 6 or more. And this means that the minimum where the Higgs field is sitting may only be a local minimum:
In the left-hand scenario we’re at a global minimum and everything is fine. In the right-hand scenario we’re not and the vacuum we see is only metastable. The Higgs mass is still positive: that’s essentially the curvature of the potential near our local minimum. But the universe will eventually tunnel through the potential barrier and we’ll all die.
Yes, that seems to be the conventional wisdom! Obviously they’re keeping it hush-hush to prevent panic.
This paper has tons of relevant references:
• Tommi Markkanen, Arttu Rajantie, Stephen Stopyra, Cosmological aspects of Higgs vacuum metastability.
Abstract. The current central experimental values of the parameters of the Standard Model give rise to a striking conclusion: metastability of the electroweak vacuum is favoured over absolute stability. A metastable vacuum for the Higgs boson implies that it is possible, and in fact inevitable, that a vacuum decay takes place with catastrophic consequences for the Universe. The metastability of the Higgs vacuum is especially significant for cosmology, because there are many mechanisms that could have triggered the decay of the electroweak vacuum in the early Universe. We present a comprehensive review of the implications from Higgs vacuum metastability for cosmology along with a pedagogical discussion of the related theoretical topics, including renormalization group improvement, quantum field theory in curved spacetime and vacuum decay in field theory.
Scott wrote:
Once again, thank you so much! This is enlightening.
If you’d like other people to benefit from it, I’m totally up for you making it into a post on Azimuth, quoting from my emails as much or as little as you want. Or you could post it on that comment thread on my blog (which is still open), or I’d be willing to make it into a guest post (though that might need to wait till next week).
I guess my one other question is: what happens to this RG flow when you go to the infrared extreme? Is it believed, or known, that the “low-energy” values of the 25 Standard Model parameters are simply fixed points in the IR? Or could any of them run to strange values there as well?
I don’t really know the answer to that, so I’ll stop here.
But in case you’re worrying now that it’s “possible, and in fact inevitable, that a vacuum decay takes place with catastrophic consequences for the Universe”, relax! These calculations are very hard to do correctly. All existing work uses a lot of approximations that I don’t completely trust. Furthermore, they are assuming that the Standard Model is valid up to very high energies without any corrections due to new, yet-unseen particles!
So, while I think it’s a great challenge to get these calculations right, and to measure the Standard Model parameters accurately enough to do them right, I am not very worried about the Universe being taken over by a rapidly expanding bubble of ‘true vacuum’.
Azimuth 
Revolutionary new theories of physics, posted as comments here, will be deleted.
Thanks for writing and posting this! One thing: my comment “I was pretty sure
couldn’t be such a sum, since then a slight change to parameters could make it negative” looks stupid without further context. Of course, a slight change to parameters could also make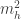 
negative, were it a precariously balanced sum (and indeed, you explained that there actually are scenarios where 
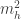would go negative and the Higgs boson would be a tachyon). What I had in mind was something more like: 
is a precariously balanced sum of positive and negative contributions; then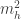 
is the only thing that’s physically relevant. In any case, all this is presumably made obsolete by the more precise picture in John’s emails.
Thanks for helping readers understand.
By the way, I think the “precariously balanced sum of positive and negative contributions” story is some sort of first-order approximation to the more accurate renormalization group story. In my roaming around, I have indeed seen formulas for the Higgs mass squared that express it as a sum of positive and negative terms. But I think the idea here is that “everything is linear to first order”.
James Blish’s novel The Triumph of Time (1959, last of the series Cities in Flight) ends with the destruction of the protagonist, human society and at least a few nearby galaxies by a naturally occurring, expanding space-time bubble like the ones you are discussing. My memory isn’t clear on whether Blish was talking about vacuum energy, but I’m sure he would have appreciated the idea.
The series contains a type of weapon named for Hans Bethe, and a communication technology named for Paul Dirac. So Blish was clearly a fan of physics, though his narrative depends on faster than light travel and communication.
That’s OK, I know I have to get it into a journal, but I enjoyed the process of writing it all down so summarily. I always expected you might delete it. Best wishes.
SA asks: “what happens to this RG flow when you go to the infrared extreme?”
I think the answer is that somewhat below
it stops. As the energy decreases, the degrees of freedom freeze out, leaving an effective field theory of only the remaining lower mass fields. Below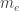 
, nothing of any interest can happen any more. In practical terms, it seems like this would already happen below the pion mass. And for weak interactions, below 
.
What if derivatives are non-existing rates, but their approximations? How to calculate errors caused by the application of infinity in integrals in this case? And how may it influence the standard model? Thanks.
Thanks for posting this discussion!
One thing I have trouble grasping is how a quantum field that is not in its ground state gets to be completely Lorentz-invariant — presumably, having a stress-energy tensor that is just a multiple of the metric.
As far as I’m aware, there is no way that classical matter, or classical electromagnetic fields, can ever give you a stress-energy tensor of that form. I can see why in a relativistic quantum field theory, the ground state of the free field where all the modes have zero quanta will be Lorentz-invariant, notwithstanding the zero-point energy in each mode. But this isn’t quite the same, is it?
So is there some easy way to see how a false vacuum pulls off the trick of being Lorentz-invariant?
One way for a free QFT, of very many, is to use a number operator analog of a thermal state. Instead of fixing a Gibbs state as![\hat A\mapsto\mathsf{Tr}[\hat A\exp(-\beta\hat H)]](https://s0.wp.com/latex.php?latex=%5Chat+A%5Cmapsto%5Cmathsf%7BTr%7D%5B%5Chat+A%5Cexp%28-%5Cbeta%5Chat+H%29%5D&bg=ffffff&fg=333333&s=0&c=20201002)
, construct ![\hat A\mapsto\mathsf{Tr}[\hat A\exp(-\mu\hat N)]](https://s0.wp.com/latex.php?latex=%5Chat+A%5Cmapsto%5Cmathsf%7BTr%7D%5B%5Chat+A%5Cexp%28-%5Cmu%5Chat+N%29%5D&bg=ffffff&fg=333333&s=0&c=20201002)
. That could be called a negative chemical potential at zero temperature, which would perhaps require interactions with a reservoir of some other field(s) for it to be maintained. 
can be defined Lorentz invariantly in terms of creation operators as ![[\hat N,a_f^\dagger]=a_f^\dagger](https://s0.wp.com/latex.php?latex=%5B%5Chat+N%2Ca_f%5E%5Cdagger%5D%3Da_f%5E%5Cdagger&bg=ffffff&fg=333333&s=0&c=20201002)
. This, like a thermal state, is not a ground state, but it can be understood to be thermodynamically stable.
Such a state doesn’t satisfy the positive spectrum condition in the Wightman axioms, but the justification for that axiom is generally taken to be “stability”: if the state being thermodynamically stable is acceptable, we’re good. The requirement that the vacuum state must be a pure state is also not satisfied by either the thermal state or the state above, but that axiom is a priori rather than based on any experimental reasoning.
So the Lorentz-invariant vacuum is a mixed state? One way to think of a mixed state is as any of various pure states with various probabilities (although unlike with classical probability, the way the mixed state is divided into pure states is somewhat arbitrary). Greg argues that no possible pure state is Lorentz-invariant, and so each picks out, say, a preferred reference frame; but each reference frame is preferred with the same probability, so the overall mixed state is still Lorentz-invariant. Is this right?
I think so, taking a Lorentz invariant convex sum of covariant pure states can be, and is in the above case, however Lorentz invariant integrals not well-defined for such cases, so IMO they should be avoided. I would for preference compute results for the state above by using the Lorentz invariant cyclic identity of the Trace and the Lorentz invariant commutator of the number operator with the creation operator (which is how I derived the expression for the generating function for this state that I give in my comment below). For a free bosonic quantum field,
![\mathsf{Tr}[\exp(i\lambda\hat\phi_f)\exp(-\mu\hat N)]=\mathsf{Tr}[\exp(i\lambda a_f^\dagger)\exp(i\lambda a_{f^*})\exp(-\mu\hat N)]\exp(-\lambda^2(f^*,f)/2)](https://s0.wp.com/latex.php?latex=%5Cmathsf%7BTr%7D%5B%5Cexp%28i%5Clambda%5Chat%5Cphi_f%29%5Cexp%28-%5Cmu%5Chat+N%29%5D%3D%5Cmathsf%7BTr%7D%5B%5Cexp%28i%5Clambda+a_f%5E%5Cdagger%29%5Cexp%28i%5Clambda+a_%7Bf%5E%2A%7D%29%5Cexp%28-%5Cmu%5Chat+N%29%5D%5Cexp%28-%5Clambda%5E2%28f%5E%2A%2Cf%29%2F2%29&bg=ffffff&fg=333333&s=0&c=20201002)
can be successively manipulated using the cyclicity and a Baker-Campbell-Hausdorff identity, with a factor 
appearing repeatedly so that one obtains a sum 
in the exponent, which becomes 
, which becomes part of the 
factor. [Sorry that’s so quick, but editing equations on Azimuth is terrifying because there’s no preview.] We’re working here with unitarily inequivalent representations of the algebra, which are, loosely put, separated by thermodynamically infinite divides.
This state could be said to be in a mixed state because it’s interacting with another Lorentz invariant field (which has been traced out) as a zero temperature bath with which it exchanges particles in a Lorentz invariant way. For any algebra of observables that doesn’t include absolutely every field (including dark matter, dark energy, or anything else we haven’t found yet, …), the state over that subalgebra must be a mixed state if there’s any interaction. For the EM field in interaction with a Dirac spinor field, for example, the vacuum state for the EM field with the Dirac spinor field traced out should be a mixed deformation of the free field vacuum state, which is pure. Haag’s theorem, after all, insists that the interacting vacuum sector must not be unitarily equivalent to the free vacuum sector.
I’ve posted the derivation I mentioned earlier to my blog, because I have in the past wanted to have it available, for which the link is: https://quantumclassical.blogspot.com/2019/02/chemical-potential-raised-states-of_28.html.
In any discussion I’ve ever seen of vacuum ev’s of fields, the only ones with non-zero expectation are (4D) scalars, for (I think) exactly the reason you mention – a vector field with an expectation value would break Lorentz invariance. (The QCD quark condensate is a pseudoscalar, but that just differs on parity transformation properties.)
The question you’re asking would already apply to the Higgs vev, even if it’s metastable and there’s a larger value with lower energy. Pretty much the definition of a scalar field is that it has trivial Lorentz transformation properties.
Thanks for the answers. I think I need to study more QFT, but maybe it will also help me understand this if I can cook up a toy classical scalar field theory with two Poincaré-invariant states with different energies.
Greg, if a quantum field has a complex structure, it already contains a classical random field of Quantum Non-Demolition measurements, so the example I give above suffices.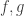
and a pre-inner product 
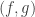on the test function space, as
![\hat\phi_f=a_{f^*}+a_f^\dagger,[a_f,a_g^\dagger]=(f,g),a_f|0\rangle=0.](https://s0.wp.com/latex.php?latex=%5Chat%5Cphi_f%3Da_%7Bf%5E%2A%7D%2Ba_f%5E%5Cdagger%2C%5Ba_f%2Ca_g%5E%5Cdagger%5D%3D%28f%2Cg%29%2Ca_f%7C0%5Crangle%3D0.&bg=ffffff&fg=333333&s=0&c=20201002)
![[\hat\phi_f,\hat\phi_g]=(f^*,g)-(g^*,f)](https://s0.wp.com/latex.php?latex=%5B%5Chat%5Cphi_f%2C%5Chat%5Cphi_g%5D%3D%28f%5E%2A%2Cg%29-%28g%5E%2A%2Cf%29&bg=ffffff&fg=333333&s=0&c=20201002)
, which is zero, satisfying microcausality, when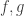 
have space-like separated supports.
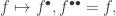for which 
which we can for the complex scalar field and, using the Hodge dual, for the empirically significant EM field, then we find for 
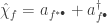that
![[\hat\chi_f,\hat\chi_g]=(f^{*\bullet},g^\bullet)-(g^{*\bullet},f^\bullet)=0](https://s0.wp.com/latex.php?latex=%5B%5Chat%5Cchi_f%2C%5Chat%5Cchi_g%5D%3D%28f%5E%7B%2A%5Cbullet%7D%2Cg%5E%5Cbullet%29-%28g%5E%7B%2A%5Cbullet%7D%2Cf%5E%5Cbullet%29%3D0&bg=ffffff&fg=333333&s=0&c=20201002)
. 
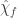is a classical random field, commuting with itself everywhere in space-time.
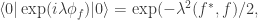
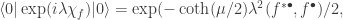
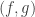fixes the connection, of different kinds, between the algebra and the space-time geometry.]
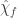is a true classical random field of QND measurements hidden away inside some quantum fields, for which we can construct isomorphisms between the random field Hilbert space and the quantum field Hilbert space, and, if we introduce the vacuum projection operator as an observable (which is routine in practical QFT but is less common in the algebraic QFT literature), we can construct an isomorphism between the algebras of observables. Which, I submit, is nice to have as well as the relatively undefined mess that is quantization. arXiv:1709.06711 has been recommended by a referee for publication, but I’m making some small changes, so not quite there.
We can present the algebraic structure of the measurement operators and vacuum state of a quantized bosonic field, using test functions
Then we find
If we can construct an involution
To show how this works through for the example above, using the number operator, for the vacuum state we can construct generating functions both for the quantum field and for the random field,
then for the higher energy state we just have
which is just to increase the Gaussian noise without increasing the commutator that ensures that the vacuum state is the minimum energy state in the vacuum sector. As I say above, this state, generated by using the number operator, is just baby steps. [Note that these generating functions and the commutation relations together are enough to fix the algebraic structure of the quantum and random fields completely. The pre-inner product
These are all trivial, albeit unconventional computations. It’s not a new theory, it’s just a new way of looking at what we’ve got. Still,
Perhaps inevitably, one mistake: the higher energy state should be written as, say,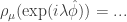
and similarly 
Hopefully there are no others.
Even if the vacuum is metastable, wouldn’t a decay only propagate at the speed of light? So, potentially there could be vacuum decays in the universe that would never reach us (if they are beyond the cosmological horizon)?
Yes, that’s possible. But one expects a more or less constant decay probabilty per volume once the Universe is no longer extremely hot, so one shouldn’t hope to “luck out” and avoid the vacuum decay forever.
For a recent detailed discussion of the “Naturalness” problem see https://arxiv.org/abs/1809.09489
which reminded me that I wrote something about this here
https://www.edge.org/response-detail/25416
It has always seemed to me that a basic problem with the “naturalness” argument is that it appears as a problem for explaining the large ratio between the GUT scale and the electroweak scale, but we have no evidence for a GUT and for an associated cutoff scale. If not the GUT scale, then the Planck scale gets invoked, but that’s again something we know nothing about.
The facts about the special nature of the low-energy Higgs parameters you discuss make me suspicious that what is really going on is some sort of conformal invariance at short distances, and that’s what’s providing the short distance boundary condition, not some new GUT physics at some particular scale.
That article was announced today on Studies in the History and Philosophy of Modern Physics, https://www.sciencedirect.com/science/article/pii/S1355219818300686. You beat me to it, Peter.
There remains a question IMO of how one decides where on the renormalization group trajectory a given experiment is, precisely, or at least in a less than an ad-hoc way, depending on details of how the experiment is constructed. The observables in QFT, distinct from the operator-valued distributions that are not observables, are supposed to be constructed as linear functionals of test functions, but if the renormalization scale is constrained by the test functions then the observables of interacting QFTs are not linear functionals of the test functions and we cannot take interacting quantum fields to be distributions, we instead have to take interacting quantum fields to be nonlinear maps from the test function space to the algebra of operators [states still have to be linear functionals so that the theory still supports a probability interpretation.]
In a field theory that is renormalizable up to arbitrarily high energies, high energies are not more fundamental, in the following sense: In order to use the renormalization group, you just need to specify the value of a running constant at some scale, and then you can use the RG to run to higher or lower energies as needed. Technically, the standard model (not including gravity) is such a field theory.
The finetuning problem arises when you regard the standard model as an effective theory which ceases to be valid above some energy because new physics (i.e. new heavy particles) enters. In this case, there is a different field theory which applies above that energy, with its own RG equations. In this case, the RG equations for the higher energy regime, provide a boundary condition for the standard model RG equations. This is what John is talking about when he mentions ε and E.
Particle physicists are in the habit of assuming there are new heavy particles for various reasons – dark matter, grand unification, monopoles, neutrino seesaw. But even if one puts all that aside, the usual trump card in an argument like this is gravity. Even if there is nothing else, at a high enough energy the standard model will have to be modified to include Planck-mass virtual black holes. And at that point you will have an enormous finetuning problem. The only alternative I can see, is that quantum gravity has a very unexpected high-energy behavior. Salvio and Strumia’s adimensional gravity is an effort in this direction, and maybe conformal gravity also has some hope of producing theories where gravitational corrections to the Higgs mass don’t produce a finetuning problem.
Two ‘out-of-the-box’ suggestions:
Could the 25 fundamental constants be uncomputable real numbers (in the sense of slide #26 of the following paper presented at Unilog2013)?
https://www.dropbox.com/s/3uaiscas7h6tolk/42_Resolving_EPR_UNILOG_2015_Presentation.pdf?dl=0
Reflecting Mitchell Porter’s comment that the “only alternative I can see, is that quantum gravity has a very unexpected high-energy behaviour”, could the limiting behaviour of some physical processes involve phase changes (singularities due to, say, hidden variables) which do not correspond to the limits of any conceivable mathematical representations of the processes (in the sense of the gedanken in Section 15: ‘The mythical completeness of metric spaces’, of the following manuscript)?
https://www.dropbox.com/s/m2qx02zqpjom90g/16_Anand_Dogmas_Submission_tHPL_Anonymous.pdf?dl=0
In answer to Scott’s last question, the standard model flows in the IR to pure electromagnetism, which is just a free theory. Everything else is massive and so freezes out in the IR.
A point which is perhaps sometimes lost is that, whatever one thinks of fine-tuning, new physics etc, the standard model as a stand-alone theory must be defined with an overall cutoff. This is because the Higgs and U(1) sectors are not asymptotically free.
In addition, it is known that
(1) The standard model is perturbatively renormalizable;
(2) In the IR it flows away from and not into the Gaussian fixed-point.
From all of this it follows that the UV theory – with a cutoff – lives somewhere close to the critical surface of the Gaussian fixed-point. One manifestation of the fact that the cutoff cannot be removed is the Landau pole.
The issue of fine tuning, such as there is one, is that since the Higgs mass suffers additive renormalization, the UV theory must be tuned to be agonizingly close to – but not quite on – the critical surface. Interestingly, for fermions, chiral symmetry ensures that the renormalized mass is proportional to the bare mass and so any tuning is much less severe.
I’m curious about what you think of the “asymptotic safety” program. It sounds very similar to what you were describing as far as finding UV fixed points in the space of RG flows.
I think the asymptotic safety program is fascinating but technically very difficult. The basic idea is that while vanilla quantum gravity is not renormalizable in the usual sense, it still might flow to an attractive ultra-violet fixed point as we increase the energy scale: just not a fixed point that’s a free field theory of gravitons! The problem is that people typically compute renormalization group flows using approximations (e.g. the “1-loop approximation”, “2-loop approximation” and so on, but also others). I worry whether these approximations can be trusted when looking for an ultraviolet fixed point for quantum gravity.
It’s not just nitpicking over rigor. I’m really worried that these approximations could break down and give seriously wrong results! You can see more specifics here:
• Jacques Distler, Asymptotic safety.