Most of us seem to agree that the promise of a dollar in the future is worth less to us than a dollar today, even if the promise is certain to be fulfilled. Economists often assume ‘exponential discounting’, which says that a dollar promised at some time 
dollars in hand at time 
Why are economists so wedded to exponential discounting? The main reason is probably that it’s mathematically simple. But one argument for it goes roughly like this: if your decisions today are to look rational at any future time, you need to use exponential discounting.
In practice, humans, pigeons and rats do not use exponential discounting. So, economists say they are ‘dynamically inconsistent’:
• Wikipedia, Dynamic inconsistency.
In economics, dynamic inconsistency or time inconsistency is a situation in which a decision-maker’s preferences change over time in such a way that a preference can become inconsistent at another point in time. This can be thought of as there being many different “selves” within decision makers, with each “self” representing the decision-maker at a different point in time; the inconsistency occurs when not all preferences are aligned.
I this ‘inconsistent’ could be a misleading term for what’s going on here. It suggests that something bad is happening. That may not be true.
Anyway, some of the early research on this was done by George Ainslie, and here is what he found:
Ainslie’s research showed that a substantial number of subjects reported that they would prefer $50 immediately rather than $100 in six months, but would NOT prefer $50 in 3 months rather than $100 in nine months, even though this was the same choice seen at 3 months’ greater distance. More significantly, those subjects who said they preferred $50 in 3 months to $100 in 9 months said they would NOT prefer $50 in 12 months to $100 in 18 months—again, the same pair of options at a different distance—showing that the preference-reversal effect did not depend on the excitement of getting an immediate reward. Nor does it depend on human culture; the first preference reversal findings were in rats and pigeons.
Let me give a mathematical argument for exponential discounting. Of course it will rely on some assumptions. I’m not claiming these assumptions are true! Far from it. I’m just claiming that if we don’t use exponential discounting, we are violating one or more of these assumptions… or breaking out of the whole framework of my argument. The widespread prevalence of ‘dynamic inconsistency’ suggests that the argument doesn’t apply to real life.
Here’s the argument:
Suppose the value to us at any time 
Let us assume:
1) The ratio
is independent of
2) The quantity 
3) The quantity
Then we can show
for some constants 
The proof goes like this. By 2) we know
for some function 
is independent of 
or in other words
Ugh! What next? Well, if we take 
Now let’s make up a variable 
or
This is beautiful except for the constant 
Then we get
A theorem of Cauchy implies that any continuous solution of this equation is of the form
So, we get
or
as desired!
By the way, we don’t need to assume 
So, assumption 3) is not the assumption I’d want to attack in trying to argue against exponential discounting. In fact both assumptions 1) and 2) are open to quite a few objections. Can you name some? Here’s one: in real life the interest rate changes with time. There must be some reason.
By the way, nothing in the argument I gave shows that 
Also, nothing in my argument for the form of 
Also, you may enjoy finding the place in my derivation where I might have divided by zero, and figure out to do about that.
If you don’t like exponential discounting—for example, because people use it to argue against spending money now to fight climate change—you might prefer hyperbolic discounting:
• Wikipedia, Hyperbolic discounting.
Azimuth 
Any comments on rationality and negative interest rates?
I find it difficult to accept how backwards it is that sustainable investment suddenly and finally makes sense in a world with piles of new negative yielding debt – but (apparently) was not a sensible option before.
And further, that negative interest rates and a catastrophic imperative to sustainable investment should by coincidence appear together (to the nearest decade or so)
http://www.lse.ac.uk/GranthamInstitute/news/uk-government-should-boost-economic-growth-by-borrowing-to-invest-in-sustainable-energy-transport-and-cities/
Thank goodness we didn’t need to fight climate change in the 80s!
Sometimes you’re offered to either: pay your bi-annual car insurance bill in full; or, make a minumum monthly payment but with an attached “partial-payment” fee. If you choose to pay in full, a lot of money gets locked up (frustrated?) in anticipation of a car accident rather than being available for some other kind of ‘accident’ such as fire or mud-slide insurance, or wanting the latest model iPhone.
The house always wins?
Hyperbolic discounting is applying the maximum entropy principle to exponential discounting, placing an uncertainty on the exponential damping rate where we only know the mean rate.
HyperbolicDiscount(t) = 1/(1+kt)
This can be cast as an odds function where the odds grow linearly over time:
Probability = 1/(1+Odds)
So the kt factor serves as an odds whereby the human brain subliminally processes when trying to make a decision based on a deferred award. Consider the decision to “I’ll either give you 100 dollars, or we can flip a fair coin and I’ll give you 300 dollars if it’s heads, nothing otherwise”. An individual may tend to choose not to risk losing the hypothetical 100 dollars because the future rewards that they can get may not outweigh the immediate payoff.
Interesting! So you’re saying
can be written as integral over 
of functions 
weighted by some function of 
(It obviously can, I’m just wondering if this is math you’re alluding to—and what’s the weighting function.)
You got it. The derivation as you describe is on the Wikipedia page for hyperbolic discounting
https://en.wikipedia.org/wiki/Hyperbolic_discounting#Uncertain_risks
I like the connection between this hyperbolic discounting and survival analysis made in the cited paper by Sozou (2015), including that the
is a survival function. Why should there be constant hazard?
In general Sozou argues that the survival function corresponding to a continuous probability density function in the hazard rate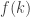
is given by the Laplace transform of that 
.
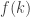Sozou goes on to show that the prior on
corresponding to hyperbolic discounting is an exponential prior.
With his (17), Sozou gives a striking survival function in the case of a uniform prior, one which is very specific.
I fell into Sozou because to John’s question, I immediate began thinking about what the posterior would be on discounts if there was a prior or some other weighting on the discount rate. And, then, I discovered Sozou did it already.
Jan, Excellent paper. Hyperbolic has to act as a survival function or cumulative as the probability density function will not integrate to unity. So the equivalent PDF for hyperbolic is the inverse squared k/(1+kt)^2
If i recall the Willard Gibbs derivation of the Boltzmann distribution used this short approach–I think its in a cheap paper back book i bought in a used book store by Tolman. It avoids the the complex combinaotrial arguments used by Boltzmann.
Irving Fisher (economist) studied under Gibbs. https://en.wikipedia.org/wiki/Irving_Fisher
It would be interesting to categorify this argument. Does the concept of discounting have a categorified meaning?
The formula G(t)*G(t’)=G(t+t’) could be generalized to a symmetric monoidal functor, or to lax and/or colax monoidal functors, by lifting ‘equality’ to ‘natural transformation’. There could be more than a gammatical connection with the exponential modality from linear logic, defined as a strong monoidal adjunction.
Clearly (2) is false. One could easily die between t and s and the older one is at t the more likely. So for someone like me, who is 81yrs old, there is a lot of difference between zero to three years in the future vs six years to nine years in the future.
Yes, good point!
Elsewhere Jason Erbele wrote:
Just a clarifying note, some of what I said in that “elsewhere” is a bit out of context here. There, the discussion included the idea that every decision, financial or otherwise, could be measured by some scalar notion of value, which one could weight by a future-devaluing function (nominally exponential). Maximizing your lifetime value would presumably provide the most self-fulfilled life.
Sorry for quoting you out of context, but it seemed worth getting people to hear this. I think a lot of economics is based on this scalar notion of value (“utility”), so it’s worth seeing what one can do in this framework, even though I’m very skeptical of it.
By the same token, it may also make a big difference depending on whether you have any fees due or not, or whether you have any other expected income or not.
If you know you’re about to get your paycheck and that’ll last you a while, it may well be the case that you feel like risking some extra time for potentially more reward.
But if you are risking dangerous levels of debt, and all the negative consequences that may come with, and that deadline is earlier than the expected payout of the larger reward, having more money right this instant is suddenly gonna be quite a bit more important. Especially if the lower reward is already enough to at least prevent/pay off that debt.
Even without considering the assumptions for exponential discounting, exponential discounting strikes me as intuitively “wrong”. The fact that our lifespans are not infinite in duration makes it difficult to accept any set of assumptions that lead to a dollar having nonzero value to a person after their death. So exponential discounting and hyperbolic discounting both are intuitively “wrong” for personal economics. For civilizations it’s still “wrong”, but it’s at least “less wrong” over human-accessible time scales.
When looking at the assumptions that exponential discounting is based on, I actually take issue with both (1) and (2). I also think there is a missing third variable in the function V – something that measures the scale. The more money you handle, the less impact one dollar makes. Much of human perception scales logarithmically (e.g. volume measured in decibels), so I wouldn’t be surprised if the third variable ended up being the logarithm of how much money is handled, rather than simply how much money is handled.
But I think a flaw with both the stated assumptions can be brought to light just by considering life expectancy tables. I don’t think this is the only flaw, but it’s the easiest to articulate. As mentioned above, I think V(t,s) should be zero if you can guarantee the beneficiary will be dead at time s. The simplest fix for this flaw would be to start with a function W(t,s) that satisfies (1) and (2), and then multiply by the conditional probability function P(alive at time s | alive at time t). The product would be a better candidate for V(t,s). It should be obvious this V(t,s) would not satisfy (2), and with a little bit of thought it should be clear that it would not satisfy (1), either.
“The fact that our lifespans are not infinite in duration makes it difficult to accept any set of assumptions that lead to a dollar having nonzero value to a person after their death.”
I think it’s very, very weird to posit that people not value their fortunes outlasting them. Why do they e.g. go to so much effort to minimize transfer taxes?
As for the scale affecting things, the Ainslie experiment was about fairly small amounts of money, either now or in the future.
People can value their fortunes outlasting them. I see no contradiction. People can experience present-day value for the present-day confidence that their fortunes will outlast them, or that their loved ones will inherit as much money as possible, but the value of those fortunes is zero to the ones who are dead. That is,
V(today, after I’m dead) > 0, but
V(after I’m dead, after I’m dead) = 0.
The only wiggle room I will grant is if you believe in an afterlife where things of value there are tied to how you handle things of value in life.
The above is only related to the value to the individual. We are part of a social fabric, so people are motivated by social value as well as individual value. The value to a society of a fortune will persist as long as that fortune and society persist, but ultimately social value will face the same fate as individual value: the social value of a dollar is zero to a society that is dead.
And regarding scale, I think it would be interesting to do a follow-up of the Ainslie experiment, where the amounts of money involved are not all small.
Yes, the connection with survival analysis is intrinsic, and, per the comment subthread above regarding the publication of Sozou, it has been addressed.
I would suggest looking into Ramsey discounting (see, e.g., https://www.nap.edu/read/24651/chapter/9), which has more basis in theory: e.g., that the social discount rate at any time should be a combination of a pure rate of time preference (sometimes estimated as the potential in any given year for civilization-ending disaster) plus the economic growth rate times the elasticity of marginal utility of consumption (e.g. the idea that a richer society cares less about an additional dollar). And then, because the economic growth rate is uncertain, using a net present value approach leads to effective discount rate that declines over time.
Sounds interesting—thanks!