The Tenfold Way

I now have a semiannual column in the Notices of the American Mathematical Society! I’m excited: it gives me a chance to write short explanations of cool math topics and get them read by up to 30,000 mathematicians. It’s sort of like This Week’s Finds on steroids.

Here’s the first one:

• The tenfold way, Notices Amer. Math. Soc. 67 (November 2020), 1599–1601.

The tenfold way became important in physics around 2010: it implies that there are ten fundamentally different kinds of matter. But it goes back to 1964, when C. T. C. Wall classified real ‘super division algebras’. He found that besides \mathbb{R}, \mathbb{C} and \mathbb{H}, which give ‘purely even’ super division algebras, there are seven more. He also showed that these ten algebras are all real or complex Clifford algebras. The eight real ones represent all eight Morita equivalence classes of real Clifford algebras, and the two complex ones do the same for the complex Clifford algebras. The tenfold way thus unites real and complex Bott periodicity.

In my article I explain what a ‘super division algebra’ is, give a quick proof that there are ten real super division algebras, and say a bit about how they show up in quantum mechanics and geometry.

For a lot more about the tenfold way, try this:

• The tenfold way.

This entry was posted on Sunday, November 22nd, 2020 at 5:54 pm and is filed under mathematics. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

14 Responses to The Tenfold Way

  1. vcvpaiva says:
    22 November, 2020 at 6:28 pm

    Wow! Congrats! looking forward to many exciting columns!

    Reply
  2. Toby Bartels says:
    22 November, 2020 at 7:26 pm

    Why are 1 and 0, but not −1, the only options for S? It seems to me that the DIII and CI rows should have −1 in the S column, and there should be an additional row, similar to AIII, still with 0 in the T and C columns, but now with −1 in the S column.

    Reply
    • John Baez says:
      22 November, 2020 at 8:05 pm

      I haven’t thought about this recently, but the basic idea is that the unlisted options you mention are equivalent to options that are listed. Here’s an analogous issue: when we have a solution of

      x^2 = -1

      in a complex algebra we can easily turn it into a solution of

      x^2 = 1

      just by multiplying x by i. But in a real algebra we can’t do this trick. If you go to my section “Ten kinds of matter, revisited” you’ll see more details about this.

      You can see this sort of thing in a distilled way in my proof that there are 10 real super division algebras: when there’s a square root of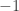 -1 around that commutes with 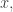x, we can convert solutions of 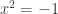x^2 = -1 into solutions of x^2 = 1 (or vice versa) so the number of non-isomorphic possibilities decreases.

      Reply
      • Toby Bartels says:
        22 November, 2020 at 8:10 pm

        So T and C live over the real numbers, but S only lives over the complex numbers, where 1 and −1 are equivalent in this way? Or am I taking the analogy too literally?

        Reply
      • John Baez says:
        22 November, 2020 at 11:21 pm

        I looked at my webpage and here’s what it said about your question:

        We start with a complex Hilbert space that may (or may not) have some operators on it called T, C and S. T stands for time reversal, C stands for charge conjugation, and S stands for the combination of charge conjugation and time reversal, which may be a symmetry even when C and T are not both symmetries.

        T and C are antiunitary, for physical reasons I will not explain here. When you apply them twice, they equal the identity up to a phase, since physically you get back where you started when you reverse the direction of time twice or switch particles and holes twice, but multiplying every state by the same phase has no physically detectable effect. Thus, we have

        T^2 = \alpha

        and

        C^2 = \beta

        for some phases (unit complex numbers) \alpha and \beta. This implies

        \alpha T = T^2 T = T T^2 = T \alpha

        but because T is antiunitary we also have

        \alpha T = T \overline{\alpha}.

        Thus we have \alpha = \overline{\alpha}, which forces \alpha =\pm 1. In short we must have T^2 = \pm 1 whenever we our substance has time reversal symmetry. The same argument shows C^2 = \pm 1 whenever it has charge conjugation symmetry.

        It follows that when we have both C and T as symmetries, S = CT is a unitary operator with S^2 = \pm 1. Indeed we shall assume S is unitary with S^2 = \pm 1 even when it’s not really built as the product of symmetries C and T. But note that since S is unitary, if S^2 = -1 we can redefine S by multiplying it by i and get S^2 = 1. We will always do this. This does not work for C and T because they are conjugate-linear: for example if C^2 = -1 then

        (iC)^2 = iCiC = -i^2 C^2

        is still -1.

        I should have just assumed S^2 = \alpha for some phase \alpha and shown that by redefining 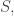S, multiplying it by a suitable phase, we can always achieve S^2 = 1. I’ve fixed my webpage so it does that.

        Reply
        • Toby Bartels says:
          22 November, 2020 at 11:31 pm

          I haven't gotten that far in the web page, but this makes sense. Ultimately, what makes S different is that it's unitary instead of antiunitary.

        • Toby Bartels says:
          23 November, 2020 at 2:39 am

          Which I guess is sort of saying that T and C live over the real numbers while S lives over the complex numbers. T and C are real-linear, but only S is complex-linear.

        • John Baez says:
          23 November, 2020 at 2:43 am

          Right. Ordinary quantum mechanics involves a curious mix of real-linear and complex-linear stuff, and quaternionic-linear stuff as well. The three-fold way and ten-fold way are ways of bringing this to the surface.

  3. Cosmo says:
    23 November, 2020 at 4:34 am

    wow i’ve only heard of eightfold way

    Reply
  4. Charles Clingen says:
    23 November, 2020 at 12:09 pm

    Fantastic!! Congratulations!!
    Charlie

    Reply
  5. preskill says:
    23 November, 2020 at 11:15 pm

    Nice article, John. I wondered why you did not cite Kitaev as well as Ryu et al. Is it because Kitaev’s paper was not published in a journal? https://arxiv.org/abs/0901.2686

    Reply
    • John Baez says:
      24 November, 2020 at 5:31 am

      I don’t think I knew about that paper. It has nothing to do with it not being in a journal.

      Thanks! Someday I’d like to write a more detailed paper on math connected to the tenfold way, and then I can cite this.

      Reply

You can use Markdown or HTML in your comments. You can also use LaTeX, like this: $latex E = m c^2 $. The word 'latex' comes right after the first dollar sign, with a space after it.

This site uses Akismet to reduce spam. Learn how your comment data is processed.