I’m giving a talk in Latham Boyle and Kirill Krasnov’s Perimeter Institute workshop Octonions and the Standard Model on Monday April 5th at noon Eastern Time.
This talk will be a review of some facts about the Standard Model. Later I’ll give one that says more about the octonions.
Can we understand the Standard Model?
Abstract. 40 years trying to go beyond the Standard Model hasn’t yet led to any clear success. As an alternative, we could try to understand why the Standard Model is the way it is. In this talk we review some lessons from grand unified theories and also from recent work using the octonions. The gauge group of the Standard Model and its representation on one generation of fermions arises naturally from a process that involves splitting 10d Euclidean space into 4+6 dimensions, but also from a process that involves splitting 10d Minkowski spacetime into 4d Minkowski space and 6 spacelike dimensions. We explain both these approaches, and how to reconcile them.
You can see the slides here, and later a video of my talk will appear. You can register to attend the talk at the workshop’s website.
Here’s a puzzle, just for fun. As I’ll recall in my talk, there’s a normal subgroup of 
This normal subgroup is isomorphic to 
where
is my favorite primitive 6th root of unity, 
is my favorite primitive cube root of unity. (I’m a primitive kind of guy, in touch with my roots.)
Here I’m turning the numbers 
But in fact there are a bunch of normal subgroups of 
Puzzle 1. Are there really exactly 12 normal subgroups of
Puzzle 2. Which ones give quotients isomorphic to the true gauge group of the Standard Model, which is 
To help you out, it helps to know that every normal subgroup of 
Here, I believe, are the 12 normal subgroups of
- The group consisting of all elements
- The group consisting of all elements
- The group consisting of all elements
- The group consisting of all elements
- The group consisting of all elements
- The group consisting of all elements
- The group consisting of all elements
- The group consisting of all elements
- The group consisting of all elements
- The group consisting of all elements
- The group consisting of all elements
- The group consisting of all elements
Azimuth 
The link to your slides is broken for me!
It should be https://math.ucr.edu/home/baez/standard/standard_web.pdf (you have a “/edu” rather than a “.edu”)
Whoops! Fixed. Thanks for catching this, David.
Pardon me for expressing a thought on octonions in advance of the talk… But if I think skeptically rather than optimistically about the idea of obtaining the standard model from octonions, I would ask whether the properties that distinguish the octonions – especially nonassociativity – are still there, playing a role in the physics, when the derivation is complete. If not, wouldn’t that suggest that the role of octonions per se is somewhat formal, and that such a derivation could proceed without them, starting with a simpler structure?
The octonions are perfectly simple, they’re just nonassociative. Anyway:
1) This talk won’t say much about the octonions; the next one will, so it might make sense to delay this discussion until then.
2) Nobody knows a “derivation” of the Standard Model from the octonions yet, in any good sense of the term, so it’s premature to worry about whether what happens when the derivation is complete. What we know so far are some intriguing connections between the octonions and the Standard Model gauge group and its representation on fermions.
3) It’s unlikely that the ideas involving octonions will succeed, but at this moment it’s unlikely that any one attempt to make progress in figuring out the fundamental laws of physics will succeed. It’s an incredibly difficult business.
In your equation defining your favorite primitive cube root of unity, the (I presume) omega is missing, at least in my browser, so the equation starts with the equal sign. The other roots appear to be defined properly.
Whoops! Thanks!
That’s better.
Two quick comments:
It can’t be true that all normal subgroups are contained in the center. For example, there is the whole group, but also
, etc..
Perhaps it’s true for all finite normal subgroups?
Here’s a quick way to see the answer to Puzzle 1 is yes. Our group of order
must be contained in 
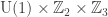. (Normality will be automatic since this is the center.) It must be contained in the unique subgroup of order 
of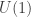 
, so we might as well assume we are working in 
.
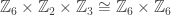So we are just asking for the number of subgroups of order
in 
. Such a group must be cyclic, so is uniquely determined by a generator. Each group has two different generators, so it is the number of elements of order 
in 
divided by 
.
An element in
has order 
if one of its coordinate does, or if the coordinates have order 
and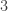 
. There are 
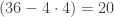of the first type, and 
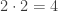of the second type, for 
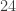elements of order 
in total (there are other ways to do this count), and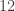 
groups of order 
.
Gabriel:
Whoops! All normal subgroups of a so-called ‘simple’ Lie group like
are contained in the center, but this is not true for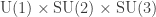 
or even 
. (Simple Lie groups are defined not to be Lie groups that are simple as groups, but Lie groups that are connected and have simple Lie algebras. Equivalently, a Lie group is simple if it’s connected and every normal subgroup is either discrete or the whole group.)
I feel that every finite normal subgroup of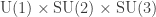
is a subgroup of the center, but I’m not going to try to prove this right now.
I like your solution to Puzzle 1 very much!
Ah, right. Well if it’s true for the factors, it must be true for the whole group: a finite normal subgroup has to project to a finite normal subgroup in each component and so, by your argument, be contained in the center in each component.
Nice! That does it, then.
Back when I was a symplectic geometer I observed that if you take a coadjoint orbit of compact G_2 (so, 12-dim) and reduce by SU(3) at a generic value (multiply by a coadjoint orbit 6-dim; then subtract twice dim SU(3)) the result is a CP^1, which could be given an action of U(2). In some sense this should be about taking a G_2-rep and extending its SU(3)-action to an (SU(3) x U(2))-action, though I don’t see the details there. When I tried to ask Sternberg about it he asked if I could compute the mass of the neutrino, so that went nowhere fast. I don’t suppose the relevant SU(3) reps have any hope of combining to a G_2 rep?
Allen wrote:
If you can’t even compute the mass of the neutrino I’m not sure I want to talk to you. But anyway, the answer to your question is yes.
I think this is how interest in octonions and the Standard Model first started. In 1973, Murat Günaydin and Feza Gürsey published a paper “Quark structure and octonions” where they noticed that SU(3) is the subgroup of G2 fixing a unit imaginary octonion (this was surely known earlier), and for each quark there is a lepton such that together their representations of SU(3) combine to give the resulting representation of SU(3) on the complexified octonions. So, this rep extends to a rep of G2.
That’s most of what I want; I also want the
action on the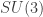 
pieces to be derivable from the overall 
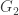action. (Obviously 
is nothing like a subgroup of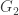 
— a rank 4 group doesn’t sit inside a rank 2 — so the derivation would have to be in a subtler sense I haven’t quite hit on.)
The following seemed interesting. I wonder if you might have time to make a quick comment on it. (Or maybe you already did?)
https://www.quantamagazine.org/a-new-map-of-the-standard-model-of-particle-physics-20201022/
{Dated, as indicated, 2020-10-22.)
It’s nice—much better than the usual pictorial depictions of the Standard Model. But for me, at least, the animated picture is less useful than the discussion in words that explains it. For example, if you don’t know that the W can change left-handed quarks of one flavor to left-handed quarks of another flavor, but not the same for right-handed quarks, it’s not clear that playing with the animation will teach you that! But maybe other people learn differently than I do.