I’ve been away from my piano since September. I really miss playing it. So, I’ve been sublimating my desire to improvise on this instrument by finally learning a bunch of basic harmony theory, which I practice just by singing or whistling.
For example, I’m getting into modes. The following 7 modes are all obtained by taking the major scale and starting it at different points. But I find that’s not the good way for me to understand the individual flavor of each one.
Much better for me is to think of each mode as the major scale (= Ionian mode) with some notes raised or lowered a half-step — since I already have an intuitive sense of what that will do to the sound:
For example, anything with the third lowered a half-step (♭3) will have a minor feel. And Aeolian, which also has the 6th and 7th lowered (♭6 and ♭7), is nothing but my old friend the natural minor scale!
A more interesting mode is Dorian, which has just the 3rd and 7th notes lowered a half-step (3♭ and 7♭). Since this 6th is not lowered this is not as sad as minor. You can play happy tunes in minor, but it’s easier to play really lugubrious tear-jerkers, which I find annoying. The major 6th of Dorian changes the sound to something more emotionally subtle. Listen to a bunch of examples here:
Some argue that the Dorian mode gets a peculiarly ‘neutral’ quality by being palindromic: the pattern of whole and half steps when you go up this mode is the same as when you go down:
This may seem crazily mathematical, but Leibniz said “Music is the pleasure the human mind experiences from counting without being aware that it is counting.”
Indeed, there is a marvelous theory of how modes sound ‘bright’ or ‘dark’ depending on how many notes are sharped—that is, raised a half-tone—or flatted—that is, lowered a half-tone. I learned about it from Rob van Hal, here:
The more notes are flatted compared to the major scale, the ‘darker’ a mode sounds! The fewer are flatted, the ‘brighter’ it sounds. And one, Lydian, is even brighter than major (= Ionian), because it has no flats and one sharp!
So, let’s list them from bright to dark. Here’s a chart from Rob van Hal’s video:
You can see lots of nice patterns here, like how the flats come in ‘from top down’ as the modes get darker: that is, starting at the 7th, then the 6th and then the 5th… but also, interspersed with these, the 3rd and then the 2nd.
But here’s something even cooler, which I also learned from Rob van Hal (though he was surely not the first to discover it).
If we invert each mode—literally turn it upside down, by playing the pattern of whole and half steps from the top of the scale down instead of from bottom to top—the brighter modes become the darker modes, and vice versa!
Let’s see it! Inverting the brightest, Lydian:
we get the darkest, Locrian:
Inverting the 2nd brightest, the happy Ionian (our familiar friend the major scale):
we get the 2nd darkest, Phrygian:
Inverting the third brightest, Mixolydian:
we get the third darkest, the sad Aeolian (our friend the natural minor):
And right in the middle is the palindromic Dorian:
What a beautiful pattern!
By the way, it’s also cool how both the ultra-bright Lydian and the ultra-dark Locrian, and only these modes, have a note that’s exactly half an octave above the 1. This is a very dissonant thing for a mode to have! In music jargon we say it like this: these modes have a note that’s a tritone above the tonic.
In Lydian this note is the sharped 4th, which is a ‘brighter than usual 4th’. In Locrian it’s the flatted 5th, which is a ‘darker than usual 5th’. But these are secretly the same note, or more technically ‘enharmonic equivalents’. They differ just in the role they play—but that makes a big difference.
Why do both Lydian and Locrian have a note that’s a tritone above the tonic? It’s not a coincidence: the tritone is mapped to itself by inversion of the octave, and inversion interchanges Lydian and Locrian!
This stuff is great, especially when I combine it with actually singing in different modes and listening to how they sound. Why am I learning it all just now, after decades of loving music? Because normally when I want to think about music I don’t study theory—I go to the piano and start playing!
The mathematics of modes
We clearly have an action of the 7-element cyclic group 
Putting these two groups together, we get an action of the 14-element dihedral group 
We’ve also seen the modes have a linear ordering by ‘brightness’. However, this ordering is preserved by the symmetries I’ve described: only the identity transformation preserves this linear ordering.
All this should have been studied in neo-Riemannian music theory, but I don’t know if it has—so if you know references, please tell me! The 
• Alissa S. Crans, Thomas M. Fiore and Ramon Satyendra, Musical actions of dihedral groups, American Mathematical Monthly 116 (2009), 479–495.
More on individual modes
For music, more important than the mathematical patterns relating different modes is learning the ‘personality’ of individual modes and how to compose or improvise well in each mode.
Here are some introductions to that! Since I’m in awe of Rob van Hal I will favor his when possible. But there are many introductions to each mode on YouTube, and it’s worth watching a lot, for different points of view.
Locrian is so unloved that I can’t find a good video on how to compose in Locrian. Instead, there’s a good one on how Björk created a top 20 hit that uses Locrian:
and also a good one about Adam Neely and friends trying to compose in Locrian:
• Part 1: modes of the major scale.
• Part 2: minor scales, and a cube of modes.
• Part 3: all 7-note scales drawn from the 12-tone chromatic scale with at most a whole tone between consecutive notes.
• Part 4: modes of the major and melodic minor scale.
• Part 5: modes of the Neapolitan major scale.
• Part 6: the special role of the Lydian mode, and the circle of fifths.
• Part 7: cycling through all 84 modes of the major scale in all keys.
• Part 8: how the group 
Azimuth 
Glad to read your take on music theory topics, here’s one interested reader. There’s even a beautiful mathematical interaction landscape worth talking about also.
If it is not premature, if one deals with the Circle of Fifths, the device used to organize tonalities and their defining sharps or flats, one can see that the alterations appearing in your ordering of modes from light to dark correspond exactly to the alterations of the tonalities in the Circle of Fifths, if one starts with G-major and goes counter-clockwise.
For instance, G-major has a single F-sharp alteration corresponding to Lydian, C-major has no alterations (Ionian), F-major has B-flat (Mixolydian), the next tonality has B-flat and E-flat alterations, and starts in B, but has the B-flat alteration, so it is the B-flat-major tonality (matching Dorian), and so on, in agreement with the alterations in the lightness ordering of modes.
So if one does the rote memory work of learning the alterations in the circle of Fifths one gets for free the recipe for all the parallel modes.
There are nice “backing tracks” for the modes in YouTube to play along and bring them home. I recall learning also with this video from Frank Gambale, where he demonstrates parallel modes in guitar.
This is really cool! I’m aware of the circle of fifths but I don’t really understand why it controls the pattern of sharps and flats in the key signatures, even though I’ve seen some discussion of it. Nor do I understand why that pattern of sharps and flats recurs in the various modes here. I should probably just work it all out myself sometime: it can’t be that hard! But it’s really nice.
There is an order: FCGDAEB. That is the order of the sharps, i.e. the key of G has one sharp (F), D has two (F and C) etc. BEADGCF, the reverse, is the order of the flats, i.e. the key of F has one flat (B), B-flat hat two (B and E) etc. The order of the keys with sharps is the same as the order of the sharps, but starting at G. The order of the keys with flats is the same as the order of the flats but starting at F.
The intervals in the sharps order are perfect fifths, those in the flats order perfect fourths. Guitars and bass guitars are tuned in fourths (with a major third between the G and B strings), the violin family in fifths (except the bass, which is tuned like a bass guitar, reflecting the fact that it has some things in common with viols, such as sloping sides; viols also had thinner wood, C-holes instead of F-holes, frets, and more strings (also occasionally seen on modern double basses and bass guitars)).
The book https://en.wikipedia.org/wiki/G%C3%B6del,_Escher,_Bach has a lot of interesting stuff on the mathematics of music (and of Escher). (Interestingly, almost all of my favourite painters and so on are from the low countries: Escher, Magritte, Vermeer, Hals, Ruisdael, Bosch, Brueghel, etc., spanning several centuries.)
Of course, this, and modulation and so on, really work only in the context of equal temperament. Equal vs. natural vs. other temperaments is a classic debate, up there with those about metric signatures in GR, VMS vs. linux, Fortran vs. C, Beatles vs. Stones, etc. :-)
Another interesting highly symmetric case is that of the octatonic scale with sequence
W-H-W-H-W-H-W-H (or H-W-H-W-H-W-H-W).
Yes! Messiaen defined modes of limited transposition to be modes with n notes that don’t give n different modes as you cycle them around… due to symmetries. The octatonic scale is the second on Messiaen’s list.
Rick Beato has a nice video where he shows what you can do with modes of limited transposition. This was the first music theory video I watched on YouTube—the very beginning of my current phase.
Beato has some good stuff. Today, I plan to watch his video about the Carpenters: https://whyevolutionistrue.com/2022/11/01/rick-beato-analyzes-karen-carpenter/
Another good YouTube music guy: https://www.youtube.com/watch?v=HmjRM3AziTY
The whole thing is worth watching, also his other videos. In the one above at 15:20, one hears John perfectly mimicking George Martin’s posh RP accent.
And here’s George Martin mimicking George’s scouse accent (from about 0:50): https://www.youtube.com/watch?v=h3AY1CVUgJw
Back in the 1970s when studying music at a local college with other children (all a bit older than I was, i.e. teenagers), I was the worst player but the best at theory.
A slight source of confusion is that there are two systems for naming modes.
I can see where you’re coming from in the way you think of modes, but I dislike that method because it puts the major scale in a “default” position. But maybe there is a reason for the default.
An interesting addition are the melodic and harmonic minor modes. The description sounds strange, but it makes sense when hearing it. A good example is the high voice on Bach’s bourree in E minor (originally for lute, but popular with guitarists; the opening of the Beatles’ “Blackbird” evolved from Paul (who used to play the Bach tune with George at parties) hearing someone mis-play it.
I described two ways of thinking about modes. The first privileges major (= Ionian), and that’s good for many purposes, especially when I’m singing or whistling, since then major is the default for me. I mentally visualize the C major scale on a piano and can then sing other modes while imagining how I’d sharp or flat various notes. Someday I’ll be able to just burst out singing in Lydian but I’m not there yet.
The second is the order of brightness, which doesn’t privilege Ionian.
Actually there are three naming schemes, as illustrated here with the Dorian mode: https://en.wikipedia.org/wiki/Dorian_mode
You’re talking about the Greek, medieval and modern modes? I think the first two are not just other systems for naming modes, but actually different modes.
I am completely unconcerned with the earlier history of modes in my current studies, since I’m just interested in better understanding how modern musicians talk about music.
Right. As in some other cases, different things are known by the same name, and the same thing is known by different names. But the system with “D for Doric” is the modern system and what we are both most interested in.
Thanks for the post! First question that comes to mind: what do the corresponding symmetries look like for the modes built from harmonic and melodic minor?
In each case the answer depends on just one thing: is one of those modes invariant under inversion, or not? For major that mode was Dorian, and its existence implied that the inversion of every mode of major is some other mode of major! (This is a little theorem.)
Let me check this for harmonic minor.
Harmonic minor has spaces between the notes like
w h w w h w t
where t means three half-steps
Let me make sure—I’ll write the spaces between the notes:
1 w 2 h 3♭ w 4 w 5 h 6♭ t 7
Yup. As we cycle
w h w w h w t
around, do we ever get a palindrome? If so t must be in the middle. So let’s cycle it until t is in the middle:
w h w t w h w
Yes, this is a palindrome! So, one of the modes of harmonic minor is invariant under inversion. So, inverting any mode of harmonic minor gives another mode of harmonic minor. They come in inverse pairs except for the one above.
For example, inverting the first mode of harmonic minor, namely harmonic minor itself
w h w w h w t
gives
t w h w w h w
which is the 7th mode of harmonic minor!
I’m a bit too tired to repeat this analysis for melodic minor, but this was a lot of fun. Thanks!
I shoulda known the Björk song would be “Army of Me”. That one is weird-sounding even by Björk standards (and it rocks).
I love that song. Anyone who hasn’t heard it yet, go here. Unfortunately for Locrian fans, the chorus
is not in Locrian. The video I linked to analyzing the song explains.
By the way, I find the video completely distracting from the original point of the song, though fun in its own right. But Björk has given a complicated explanation of the symbolic meaning of this video, so maybe I missed the original point of the song.
Ohne Musik wäre die Welt ein Irrtum. —Friedrich Nietzsche
Thinking a bit more mathematically:
We can start with the group
. These group elements are ways of transposing notes in a chosen 7-note mode. Addition is composing these transpositions.
The set of modes of the major scale is a torsor for this group: that is, the group acts on these modes freely and transitively.
Geometrically we can think of
or any torsor for this group, as a copy of ‘the affine line’ for the field 
Geometrically transpositions would be called ‘translations’ of the affine line.
But then we start talking about inversion, which is an automorphism of the group
. If we let this and transpositions generate a group we get the dihedral group 
But this is just part of a larger group: the group of of affine transformations of the affine line. Wikipedia would call this larger group the affine group
Here
is the group of units of 
which is isomorphic to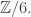 
It has the identity 1, a unique element of order 2 (which is our friend inversion, namely -1), two elements of order 3 (namely 4 and 5) and two of order 6 (namely -4 = 3 and -5 = 2).
I don’t know if this group
acts in any musically interesting way on the 7 notes of the diatonic scale. So, it’s probably a weird idea to go even further and look at larger groups. But it’s hard not think about larger groups like 
(here) and 
(here), which are so important in mathematics.
It sounds so interesting, because of all the regularity hidden in there, but my experience with music theory is, unfortunately, that I don’t understand much of it, because of the terrible way of naming stuff, mainly for historical reasons. I guess, now it’s too late, to start to rewrite all of it in some meaningful mathematical way?
Candidate for one of the stupidest things of all time, at least in music (and maybe outside it as well): in German, the note B is called H. CDEFGAHC. Really. That is because in some Fraktur scripts the two letters look almost indistinguishable. Still, logic alone dictates that it should be B. But there is also a note B. What is it? B-flat. (The flat symbol sort of looks like a B, which is probably the origin, not the missing B in the scale.)
But it did mean that BACH could use his name in a theme, which he did in several pieces (and some composers after him). There is a story that he died when he (blind) dictated it for the last time; modern scholars take it as a myth, even though started by one of JSB’s sons (CPEB): https://en.wikipedia.org/wiki/The_Art_of_Fugue#Fuga_a_3_Soggetti
From the same Wikipedia page: “ Sylvestre and Costa[15] reported a mathematical architecture of The Art of Fugue, based on bar counts, which shows that the whole work was conceived on the basis of the Fibonacci series and the golden ratio. The significance of the mathematical architecture can probably be explained by considering the role of the work as a membership contribution to the Correspondierende Societät der musicalischen Wissenschaften [de], and to the “scientific” meaning that Bach attributed to counterpoint.”
Erno Lendvai’s ‘Bela Bartok An Analysis of His Music’ (1971) identifies/misidentifies golden ratios throughout Bartok’s work. Free pdf here: https://bit.ly/3EeCd9R. I decided when I read this that Lendvai was shoehorning his meme wherever he could see it. There was a study of award-winning Hollywood classics idenfiying the denouments a golden ratio through the film, the prime example being ‘The Maltese Falcon’. Having a climax about 2/3s of the way through would be Goldilock’s porridge just right for a story. looking for the free pdf I found this critique of Lendvai: Gareth Roberts, ‘Erno Lendvai and the Bartok Controversy’: https://bit.ly/3UkaeLEhttps://bit.ly/3UkaeLE. It’s from the fun titled: ‘MAA Session on Good Math from Bad:
Crackpots, Cranks, and Progress, 2018 Joint Mathematics Meetings San Diego, CA January 10–13, 2018’
Wolfgang wrote:
I think it’s largely pointless to dream of better notations for music unless you already know a lot of music theory: it mainly serves as a way to put off learning the subject.
It reminds me a lot of how some computer programmers come up with brilliant suggestions for how to revamp mathematical notation, arguing that they would be able to understand math if only the existing notation weren’t so bad. Usually their proposed changes make math look more like—surprise!—computer programs. But this neglects that math is something we scribble on whiteboards and pads of paper while talking to other mathematicians or doing little calculations ourselves.
Similarly, every now and then some genius comes along and says that instead of calling the notes things like A, B♭ or C♯ we should just number all the notes in the chromatic scale 1,2,3,…,12, or maybe 0,1,2,…11. Or maybe we should create pianos without those weird patterns of white and black keys, and just have white keys. All this neglects how western music actually works! If someone says something like this, it’s probably good to ask them what’s the difference between C♯ and D♭. And have they ever tried playing a piano where all the keys look the same?
I can certainly imagine improvements that could be made here and there, if we were able to push a “reset” button on civilization and start again. But there really are reasons for many of the strange things musicians do, and the only way to learn those reasons is to dive in and study music as it actually is.
You’re possibly right. I guess anyhow the ones like me demanding a better notation should possibly take up the hard work to invent one, which would first require an intense study of the notation deemed inferior, unless one possibly realizes on the way that it is not that bad at all :). So the frustration is still there, but it should possibly be more understood as myself being frustrated about my own shortcomings to learn music theory than shortcomings of music theory itself.
Without spending sufficient time on this, I’m a bit confused. I think it might help to start with the 12 intervals of the well-tempered chromatic scale (first of all, why 12?), and then explain why a certain circular pattern of seven whole and half steps is chosen as particularly interesting mathematically or musically (forming the diatonic scale and its modes). I think it must have to do with chord ratios. Maybe you have already explained this somewhere. Feel free to ignore these questions as the ramblings of an ignoramus.
I think that it is more the other way around. Start with the tonic (first of the scale). Add a fifth above and a fifth below. That is the same as a fourth below and a fourth above. The difference between the fourth and fifth is a whole tone. Start at the tonic and add whole-tone steps, for example C D E. Then there is a half step up to the fourth, F. Then after the fifth, G, whole steps again: G, A, B, leaving a half step up to C. Those are the 7 basic notes and the pattern of whole and half steps. The other 5 (the black keys, so to speak) come in when you start the same pattern on another note (say starting on G means that you need F# instead of F). (If you start on another note but keep the same notes, rather than the same intervals, then you get the other modes rather than the other keys.)
Why the fifth? Frequency ratio is 3:2, the next complicated from the 2:1 octave. Fourth is 4:3. And so on. But the right notes thus constructed in one key will be a bit off in another key, hence the equal-temperament system.
(In my previous question I misspoke: I wanted to ask about equal temperament, not well-tempered scales). I see from Wikipedia that, although Western music tradition usually divides the octave into 12 (equal?) intervals, some music has been written using 19, 24 or 31 intervals. I also saw that the “pseudo-octave” (an octave plus a fifth) has been divided into 13 equal intervals. With equal temperament all scales are equivalent, right? I guess that different tuning methods are striving to get the best compromise between simple frequency ratios and equal intervals. Is there a mathematical way to help think about all this?
While this is very interesting, it’s not what I’m interested in now. Right now I’m trying to get better at conceptualizing western music as it’s actually practiced. In particular, I’m trying to get to the point of understanding how classical and jazz musicians talk. Here’s a typical thing they’d say when explaining the basics of jazz:
Or here’s how they’d discuss a chord in classical music:
But anyway:
For why a 7-tone scale or 12-tone scale is nice, remember that the simplest nontrivial chord is an octave, with a frequency ratio of 2. Ideally we’d like to chop it into
equal parts—
steps each with frequency ratio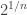 
—while making sure that we get nice fractions like 3/2 and 4/3 showing up as frequency ratios between notes in our scale.
But these goals are incompatible since all the
th roots of 2 are irrational (except for the first root, you smart-alecks out there). So it’s a matter of compromise. And it turns out that the numbers 7 and 12 naturally show up when we seek fairly simple good compromises.
There’s a lot of math here, and different competing theories. Philip Helbig’s answer is very nice. Here’s something else that’s pretty simple and fun:
• Michael Rubinstein, Why 12 notes to the octave?
If you read other articles you’ll get even more theories.
In everything I’m doing now, I’m taking the 12-tone equal-tempered scale for granted and trying to learn how modern western musicians uses it. The modes I listed are a way to get some spice just by starting the major scale on a different note.
Thanks for the thoughtful reply. I found the discussion of continued fractions by Michael Rubinstein very interesting, and was intrigued that a 19-step octave was a viable alternative to the 12-step scale.
Good luck understanding musicians! Reminds me of trying to penetrate the jargon of art critics in an undergraduate art appreciation class.
It’s completely different: unlike the somewhat vague rhetoric of art criticism, the terminology of musicians is usually, like math, just a terse way of communicating something utterly precise.
To take one example from my quotes, a “iim7 chord” is a chord containing the 2nd, 4th, 6th and 8th notes in a major scale. Calling it “iim7” immediately tells us that it starts on the 2nd note and that the sound of this chord is a “minor 7th” meaning that after the starting note we go up first 3 half steps, then 3 more, then 3 more. 7th chords are incredibly important in western music, they come in different kinds, and there are lots of people on YouTube eager to help you learn how they sound and how to play them. (If you click on this you’ll hear a minor 7th chord.)
So, I find this stuff quite pleasant. Of course like math, it take patience, one has to study it a little bit each day and go on for months or years… but it gets easier and easier as you go, because it’s a coherent system.
Sorry, I made a very poor analogy, and I really knew better. The only similarity was my initial lack of understanding of the conversations in both fields; however, I fully recognize that true, unambiguous meaning lies behind the musician’s words, but I felt the art critics’ words were pretentious fluff.
“Reminds me of trying to penetrate the jargon of art critics in an undergraduate art appreciation class.”
Many singers are instantly recognizable and uniquely by their vocal tone.
“The nature of the features that allow us
to distinguish voices with such certainty is still unknown” — Mesaros, A., & Astola, J. (n.d.). Inter-dependence of spectral measures for the singing voice. International Symposium on Signals, Circuits and Systems, 2005. ISSCS 2005. doi:10.1109/isscs.2005.1509915
Not sure if further progress has been made.
Steve wrote:
Okay, good! I don’t really want to start complaining about art critics, but I feel that music theory terminology is quite different.
I just noticed that if you continue along the circle of fifths beyond Locrian, and flat the next note in the sequence BEADG -> C, it closes the pattern only half-step down, producing C-flat Lydian. Assuming I’m looking at this correctly.
Hmm, I’ll have to think about that! It sounds vaguely reasonable that we loop back to Lydian.
I believe it does. Starting with C Lydian, then flat the 4th (F) to get C Ionian, then, in order, flat the 7th (B), 3rd (E), 6th (A), 2nd (D), and then 5th (G) to get Locrian. The next note in the circle of fifths, and the only note in the scale left un-flatted from C Lydian, is the 1st/root, C. So the next “mode” is flat the entire C Lydian scale, or C-flat Lydian. It then follows that continuing the pattern will eventually produce every mode in every key, finally winding up at C Lydian again.
It might be fun to create an animation of this over one octave on a piano keyboard, seeing the modes slowly flow downward though the keys, ending up on the original pattern an octave down.
George Russell’s ‘Lydian chromatic theory of tonal organisation. The art and science of tonal gravity’ is a, and possibly the, jazz standard text used by Davis, Monk, Coltrane and all the bebop greats. Free pdf here: https://bit.ly/3DHoBm8
I’ve heard of that book. I should give it a look and see if I know enough to understand it yet. At least I know what the Lydian mode is! I’ve been singing it repeatedly… still haven’t made it my own, though.
[…] John Baez has been putting out an excellent series of posts about music theory on his blog. The most recent, the seventh, is about how you can generate scales by picking out piano notes in int… What’s interesting is that you can generate all seven major scale modes in each of the twelve […]