Mathematics of the Environment (Part 9)

I didn’t manage to cover everything I intended last time, so I’m moving the stuff about the eccentricity of the Earth’s orbit to this week, and expanding it.

Sunshine and the Earth’s orbit

I bet some of you are hungry for some math. As I mentioned, it takes some work to see how changes in the eccentricity of the Earth’s orbit affect the annual average of sunlight hitting the top of the Earth’s atmosphere. Luckily Greg Egan has done this work for us. While the result is surely not new, his approach makes nice use of the fact that both gravity and solar radiation obey an inverse-square law. That’s pretty cool.

Here is his calculation with some details filled in.

Let’s think of the Earth as moving around an ellipse with one focus at the origin. Its angular momentum is then

\displaystyle{ J = m r v_\theta }

where m is its mass, r and \theta are its polar coordinates, and v_\theta is the angular component of its velocity:

\displaystyle{ v_\theta = r \frac{d \theta}{d t} }

So,

\displaystyle{ J = m r^2 \frac{d \theta}{d t} }

and

\displaystyle{\frac{d \theta}{d t} = \frac{J}{m r^2} }

Since the brightness of a distant object goes like 1/r^2, the solar energy hitting the Earth per unit time is

\displaystyle{ \frac{d U}{d t} = \frac{C}{r^2}}

for some constant C. It follows that the energy delivered per unit of angular progress around the orbit is

\displaystyle{ \frac{d U}{d \theta} = \frac{d U/d t}{d \theta/ dt} = \frac{C m}{J} }

Thus, the total energy delivered in one period will be

\begin{array}{ccl} U &=& \displaystyle{ \int_0^{2 \pi} \frac{d U}{d \theta} \, d \theta} \\ \\ &=& \displaystyle{ \frac{2\pi C m}{J} } \end{array}

So far we haven’t used the the fact that the Earth’s orbit is elliptical. Next we’ll do that. Our goal will be to show that U depends only very slightly on the eccentricity of the Earth’s orbit. But we need to review a bit of geometry first.

The geometry of ellipses

If the Earth is moving in an ellipse with one focus at the origin, its equation in polar coordinates is

\displaystyle{ r = \frac{p}{1 + e \cos \theta} }

where e is the eccentricity and p is the somewhat dirty-sounding semi-latus rectum. You can think of p as a kind of average radius of the ellipse—more on that in a minute.

Let’s think of the origin in this coordinate system as the Sun—that’s close to true, though the Sun moves a little. Then the Earth gets closest to the Sun when \cos \theta is as big as possible. So, the Earth is closest to the Sun when \theta = 0, and then its distance is

\displaystyle{ r_1 = \frac{p}{1 + e} }

Similarly, the Earth is farthest from the Sun happens when \theta = \pi, and then its distance is

\displaystyle{ r_2 = \frac{p}{1 - e} }

We call r_1 the perihelion and r_2 the aphelion.

The semi-major axis is half the distance between the opposite points on the Earth’s orbit that are farthest from each other. This is denoted a. These points occur at \theta = 0 and \theta = \pi, so the distance between these points is r_1 + r_2, and

\displaystyle{ a = \frac{r_1 + r_2}{2} }

So, the semi-major axis is the arithmetic mean of the perihelion and aphelion.

The semi-minor axis is half the distance between the opposite points on the Earth’s orbit that are closest to each other. This is denoted b.

Puzzle 1. Show that the semi-minor axis is the geometric mean of the perihelion and aphelion:

\displaystyle{ b = \sqrt{r_1 r_2} }

I said the semi-latus rectum p is also a kind of average radius of the ellipse. Just to make that precise, try this:

Puzzle 2. Show that the semi-latus rectum is the harmonic mean of the perihelion and aphelion:

\displaystyle{ p = \frac{1}{\frac{1}{2}\left(\frac{1}{r_1} + \frac{1}{r_2}\right) } }

This puzzle is just for fun: the Greeks loved arithmetic, geometric and harmonic means, and the Greek mathematician Apollonius wrote a book on conic sections, so he must have known these facts and loved them. The conventional wisdom is that the Greeks never realized that the planets move in elliptical orbits. However, the wonderful movie Agora presents a great alternative history in which Hypatia figures it all out shortly before being killed! And the mathematician Sandro Graffi (who incidentally taught a course I took in college on the self-adjointness of quantum-mechanical Hamiltonians) has claimed:

Now an infrequently read work of Plutarch, several parts of the Natural History of Plinius, of the Natural Questions of Seneca, and of the Architecture of Vitruvius, also infrequently read, especially by scientists, clearly show that the cultural elite of the early imperial age (first century A.D.) were fully aware of and convinced of a heliocentric dynamical theory of planetary motions based on the attractions of the planets toward the Sun by a force proportional to the inverse square of the distance between planet and Sun. The inverse square dependence on the distance comes from the assumption that the attraction is propagated along rays emanating from the surfaces of the bodies.

I have no idea if the controversial last part of this claim is true. But it’s fun to imagine!

More importantly for what’s to come, we can express the semi-minor axis in terms of the semi-major axis and the eccentricity. Since

\displaystyle{ r_1 = \frac{p}{1 + e} , \qquad r_2 = \frac{p}{1 - e} }

we have

\displaystyle{ r_1 + r_2 = \frac{p}{1 + e} + \frac{p}{1 - e} = \frac{2 p}{1 - e^2} }

so the semi-minor axis is

\displaystyle{ a = \frac{p}{1 - e^2} }

while

\displaystyle {r_1 r_2 = \frac{p^2}{1 - e^2} }

so the semi-major axis is

\displaystyle { b = \frac{p}{\sqrt{1 - e^2}} }

and thus they are related by

b = a \sqrt{1 - e^2}

Remember this!

How total annual sunshine depends on eccentricity

We saw a nice formula for the total solar energy hitting the Earth in one year in terms of its angular momentum J:

\displaystyle{ U = \frac{2\pi C m}{J} }

How can we relate the angular momentum J to the shape of the Earth’s orbit? The Earth’s energy, kinetic plus potential, is constant throughout the year. The kinetic energy is

\frac{1}{2}m v^2

and the potential energy is

\displaystyle{ -\frac{G M m}{r} }

At the aphelion or perihelion the Earth isn’t moving in or out, just around, so by our earlier work

\displaystyle{v = v_\theta = \frac{J}{m r} }

and the kinetic energy is

\displaystyle{ \frac{J^2}{2 r^2} }

Equating the Earth’s energy at aphelion and perihelion, we thus get

\displaystyle{\frac{J^2}{2m r_1^2} -\frac{G M m}{r_1} = \frac{J^2}{2m r_2^2} -\frac{G M m}{r_2} }

and doing some algebra:

\displaystyle{\frac{J^2}{2m} \left(\frac{1}{r_1^2} - \frac{1}{r_2^2}\right) = G M m \left( \frac{1}{r_1} - \frac{1}{r_2} \right) }

\displaystyle{\frac{J^2}{2m} \left(\frac{r_2^2 - r_1^2}{r_1^2 r_2^2}\right) = G M m \left( \frac{r_2 - r_1}{r_1 r_2} \right) }

\displaystyle{\frac{J^2}{2m} \left(\frac{r_1 + r_2}{r_1 r_2}\right) = G M m }

and solving for J,

\displaystyle{ J = m \sqrt{\frac{2 G M r_1 r_2}{r_1 + r_2}} }

But remember that the semi-major and semi-minor axis of the Earth’s orbit are given by

\displaystyle{ a=\frac{1}{2} (r_1+r_2)} , \qquad \displaystyle{ b=\sqrt{r_1 r_2} }

respectively! So, we have

\displaystyle{ J = mb \sqrt{\frac{GM}{a}} }

This lets us rewrite our old formula for the energy U in the form of sunshine that hits the Earth each year:

\displaystyle{ U=\frac{2\pi C m}{J} = \frac{2\pi C}{b} \sqrt{\frac{a}{G M}} }

But we’ve also seen that

b = a \sqrt{1 - e^2}

so we get the formula we’ve been seeking:

\displaystyle{U=\frac{2\pi C}{\sqrt{G M a (1-e^2)}}}

This tells us U as a function of semi-major axis and eccentricity.

As we’ll see later, the semi-major axis a is almost unchanged by small perturbations of the Earth’s orbit. The main thing that changes is the eccentricity e. But if e is small, e^2 is even smaller, so U doesn’t change much when we change e.

We can make this more quantiative. Let’s work out how much the actual changes in the Earth’s orbit affect the amount of solar radiation it gets! As we’ll see, the semi-major axis is almost constant, so we can ignore that. Complicated calculations we can’t redo here show that the eccentricity varies between 0.005 and 0.058. We’ve seen the total energy the Earth gets each year from solar radiation is proportional to

\displaystyle{ \frac{1}{\sqrt{1-e^2}} }

When the eccentricity is at its lowest value, e = 0.005, we get

\displaystyle{ \frac{1}{\sqrt{1-e^2}} = 1.0000125 }

When the eccentricity is at its highest value, e = 0.058, we get

\displaystyle{\frac{1}{\sqrt{1-e^2}} = 1.00168626 }

So, the solar power hitting the Earth each year changes by a factor of

\displaystyle{1.00168626/1.0000125 = 1.00167373 }

In other words, it changes by merely 0.167%.

That’s very small And the effect on the Earth’s temperature would naively be even less!

Naively, we can treat the Earth as a greybody: an ideal object whose tendency to absorb or emit radiation is the same at all wavelengths and temperatures. Since the temperature of a greybody is proportional to the fourth root of the power it receives, a 0.167% change in solar energy received per year corresponds to a percentage change in temperature roughly one fourth as big. That’s a 0.042% change in temperature. If we imagine starting with an Earth like ours, with an average temperature of roughly 290 kelvin, that’s a change of just 0.12 kelvin!

The upshot seems to be this: in a naive model without any amplifying effects, changes in the eccentricity of the Earth’s orbit would cause temperature changes of just 0.12 °C!

This is much less than the roughly 5 °C change we see between glacial and interglacial periods. So, if changes in eccentricity are important in glacial cycles, we have some explaining to do. Possible explanations include season-dependent phenomena and climate feedback effects, like the ice albedo effect we’ve been discussing. Probably both are very important!

Adiabatic invariance

Why does the semi-major axis of the Earth’s orbit remain almost unchanged under small perturbations? The reason is that it’s an ‘adiabatic invariant’. This is basically just a fancy way of saying it remains almost unchanged. But the point is, there’s a whole theory of adiabatic invariants… which supposedly explains the near-constancy of the semi-major axis.

According to Wikipedia:

The Earth’s eccentricity varies primarily due to interactions with the gravitational fields of Jupiter and Saturn. As the eccentricity of the orbit evolves, the semi-major axis of the orbital ellipse remains unchanged. From the perspective of the perturbation theory used in celestial mechanics to compute the evolution of the orbit, the semi-major axis is an adiabatic invariant. According to Kepler’s third law the period of the orbit is determined by the semi-major axis. It follows that the Earth’s orbital period, the length of a sidereal year, also remains unchanged as the orbit evolves. As the semi-minor axis is decreased with the eccentricity increase, the seasonal changes increase. But the mean solar irradiation for the planet changes only slightly for small eccentricity, due to Kepler’s second law.

Unfortunately, even though I understand a bit about the general theory of adiabatic invariants, I have not gotten around to convincing myself that the semi-major axis is such a thing, for the perturbations experienced by the Earth.

Here’s something easier: checking that the semi-major axis of the Earth’s orbit determines the period of the Earth’s orbit, say T. To do this, first relate the angular momentum to the period by integrating the rate at which orbital area is swept out by the planet:

\displaystyle{\frac{1}{2} r^2 \frac{d \theta}{d t} = \frac{J}{2 m} }

over one orbit. Since the area of an ellipse is \pi a b, this gives us:

\displaystyle{ J = \frac{2 \pi a b m}{T} }

On the other hand, we’ve seen

\displaystyle{J = m b \sqrt{\frac{G M}{a}}}

Equating these two expressions for J shows that the period is:

\displaystyle{ T = 2 \pi \sqrt{\frac{a^3}{G M}}}

So, the period depends only on the semi-major axis, not the eccentricity. Conversely, we could solve this equation to see that the semi-major axis depends only on the period, not the eccentricity.

I’m treating G and M as constants here. If the mass of the Sun decreases, as it eventually will when it becomes a red giant and puffs out lots of gas, the semi-major axes of the Earth’s orbit will change. It will actually increase! This is one reason people are still arguing about just when the Earth will get swallowed up by the Sun:

• David Appell, The Sun will eventually engulf the Earth—maybe, Scientific American, 8 September 2008.

And, to show just how subtle these things are, if the mass of the Sun slowly changes, while the semi-major axis of the Earth’s orbit will change, the eccentricity will remain almost unchanged. Why? Because for this kind of process, it’s the eccentricity that’s an adiabatic invariant!

Indeed, I got all excited when I started reading a homework problem in Landau and Lifschitz’s book Classical Mechanics, which describes adiabatic invariants for the gravitational 2-body problem. But I was bummed out when they concluded that the eccentricity was an adiabatic invariant for gradual changes in M. They didn’t discuss any problems for which the semi-major axis was an adiabatic invariant.

I’ll have to get back to this later sometime, probably with the help of a good book on celestial mechanics. If you’re curious about the concept of adiabatic invariant, start here:

• Adiabatic invariant, Wikipedia.

and then try this:

• Marko Robnik, Theory of adiabatic invariants, February 2004.

And if you know how to show the Earth’s semi-major axis is an adiabatic invariant, please tell me how!

This entry was posted on Tuesday, November 27th, 2012 at 11:29 pm and is filed under astronomy, climate, mathematics. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

13 Responses to Mathematics of the Environment (Part 9)

  1. Uwe Stroinski says:
    28 November, 2012 at 10:50 am

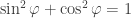    A quick and dirty solution of puzzle 1. We need to maximize r \sin\varphi. For that purpose we use \sin^2\varphi +\cos^2\varphi = 1 and solve the equation of the ellipse

    r \sin\varphi = \frac{1}{e}\sqrt{(e^2-1)r^2+2pr-p^2}

    It suffices to differentiate ‘below the square root’ and to solve the resulting linear equation for the maximum r = \frac{p}{1-e^2}. Plugging this into the equation for r \sin\varphi yields the result.

    Reply
  2. arch1 says:
    28 November, 2012 at 4:27 pm

    It is very pretty how this discussion of the ellipse incorporates five commonly encountered special cases of the generalized mean of r1 and r2 (arithmetic, geometric, harmonic, min (r1 itself), and max (r2 itself)).

    Is it too much to hope that the sixth commonly encountered special case of the generalized mean (namely, root mean square) can be naturally incorporated as well?

    Reply
    • John Baez says:
      28 November, 2012 at 9:17 pm

      I don’t know! This book mentions the root mean square or quadratic mean of the perihelion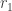 r_1 and aphelion r_2:

      \displaystyle{ \sqrt{\frac{r_1^2 + r_2}{2}} }

      and says that it equals

      a \sqrt{1 + e^2}

      where a is the semi-major axis and e is the eccentricity, but it doesn’t give any geometrical interpretation of this quantity. It just does so for the arithmetic, geometric and harmonic means.

      I would like to know who first discovered these facts about means and ellipses. If Apollonius didn’t know them, I’ll be very disappointed.

      Reply
      • arch1 says:
        28 November, 2012 at 10:29 pm

        Thanks, very interesting. BTW an apparent typo in your original posting:
        1) 2nd occurrence of “so the semi-major axis is”: change major to minor

        Reply
        • John Baez says:
          28 November, 2012 at 10:35 pm

          I’ll check that out and fix it if needed. Thanks!

        • arch1 says:
          29 November, 2012 at 10:04 pm

          1) The semi-latus rectum can be geometrically interpreted as a line from a focal pt to the ellipse, drawn parallel to the minor axis. Five down, one to go:-)
          2) I too couldn’t find (in the sense of “search”, not in the sense of “think hard” like Apollonius) a geometrical interpretation of the Quadratic mean of r1 and r2, though I suspect one exists.
          3) A nice geometric interpretation of the six means – min, H, G, A, Q, & max – of two numbers, in the context of a circle rather than of a general ellipse, is at: http://en.wikipedia.org/w/index.php?title=File:MathematicalMeans.svg&page=1
          4) Nothing major but the major you made minor should be major and the major you kept major should be minor:-)

  3. John Baez says:
    28 November, 2012 at 10:46 pm

    By the way, in class I titled one section of my talk ‘Sunshine and eccentricity’, and mentioned that this was a good description of California.

    Reply
  4. Greg Egan says:
    29 November, 2012 at 12:42 am

    If you accept that the sum of the distances between any point on an ellipse and the two foci is a constant, Puzzle 1 is easy.

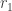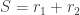    Let c be half the distance between the foci, r_1 the perihelion distance and r_2 the aphelion distance. Then the sum of distances S to the foci at perihelion is 2r_1+2c, the sum of distances to the foci at aphelion is 2r_2-2c, and equating them gives us c=\frac{1}{2}(r_2-r_1) and S=r_1+r_2.

    When the planet lies on the minor axis, which bisects the line between the foci, by symmetry and Pythagoras the semi-minor axis b is given by:

    b^2=\left(\frac{S}{2}\right)^2-c^2 \\ = \frac{1}{4}\left((r_1+r_2)^2-(r_2-r_1)^2\right)\\ = r_1 r_2

    The nicest proof that the sum of the distances to the foci is constant involves the Dandelin spheres, and you can see it illustrated
    here.

    Reply
  5. Greg Egan says:
    29 November, 2012 at 1:44 am

    Puzzle 2 is straightforward algebra from r_1=\frac{p}{1+e}, r_2=\frac{p}{1-e}, but there’s a typo in the formula for the harmonic mean, which should be:

    p=\frac{2}{\frac{1}{r_1}+\frac{1}{r_2}}

    Reply
  6. Mathematics of the Environment (Part 10) « Azimuth says:
    4 December, 2012 at 4:22 am

    The Milankovich cycles that most closely match this are two cycles in the eccentricity of the Earth’s orbit which have periods of 95 and 123 thousand years. But as we saw last time, these have very tiny effects on the average solar energy hitting the Earth year round […]

    Reply

You can use Markdown or HTML in your comments. You can also use LaTeX, like this: $latex E = m c^2 $. The word 'latex' comes right after the first dollar sign, with a space after it.

This site uses Akismet to reduce spam. Learn how your comment data is processed.