guest post by John Roe
• Michael Blastland and Andrew Dilnot, Commonsense Guide to Understanding Numbers in the News, in Politics, and in Life, Gotham, New York, 2008. (Review at New York Times.)
In Mathematics for Sustainability 1 I explained that I want to develop a new Gen Ed course “to enable students to develop the quantitative and qualitative skills needed to reason effectively about environmental and economic sustainability”. With this as the general objective, what are some of the specific content areas that the course should address, and what should be the specific objectives within each content area?
Right now, I see four mathematical content areas:
• Measuring
• Changing
• Networking
• Risking
Measuring – using numbers (including “large” and “small” numbers) to get an idea of the size and significance of things. Including, for instance: physical units, prefixes (mega, giga, nano, and all that), percentages/ratios, estimation, reliability. That’s a list of concepts on the math side but of course the examples should be sustainability focused. So I’d like the students to be able to answer questions like
• An inch of rain falls over a forest plot of an area 3.21 square miles. How many tons of water fall?
• Roughly, what is the total mass of carbon dioxide in the
Earth’s atmosphere at present?
• Suppose that a nuclear accident spreads 2.3 grams of cesium-137 uniformly over an area of 900 square miles. Compare the radioactivity from this source with the natural background.
• On average, how many gallons of gasoline per second are burned on the Pennsylvania Turnpike?
• A 10-acre farm near State College can produce enough food to support how many people on a vegetarian diet? On a “standard American” diet?
• Roughly, how many birds do you think there are in the world? How accurate do you think your estimate is?
Of course, part of “being able to answer” such questions is being able to know what additional questions to ask in order to give reasonable answers.
I am looking at several books in order to get a handle on this part of the course. Right now I am reading The Numbers Game by Blastland and Dilnot. It starts with an arresting example: how many centenarians are there in the US? That should be easy: just count, right? In fact, census returns ask people to report their age. But the self-reported numbers vary wildly and are estimated to be exaggerated by factors of 20 or more in some cases. Starting from this example, the book seems to give a good overview both of the difficulty and the importance of measuring, both in absolute and relative terms.
Any more suggestions for this part? Thanks!
I am thinking now to put the important distinction between stocks and flows in this section too. (We have to know what we are measuring!) Logically, it might belong in the Changing section but pedagogically it seems better here. A reader on Azimuth sent me a link to this interesting paper which points out how important the stock/flow distinction is in public (mis)understanding of the greenhouse effect:
• John D. Sterman and Linda Booth Sweeney, Understanding public complacency about climate change: adults’ mental models of climate change violate conservation of matter, Climatic Change 80 (2007), 213-238.


Two of these were mentioned before by Dan:
• Lawrence Weinstein and John A. Adam, Guesstimation: Solving the World’s Problems on the Back of a Cocktail Napkin, Princeton U. Press, Princeton, New Jersey, 2008.
• Lawrence Weinstein, Guesstimation 2.0: Solving Today’s Problems on the Back of a Napkin, Princeton U. Press, Princeton, New Jersey, 2012.
• John Harte, Consider a Spherical Cow: A Course in Environmental Problem Solving, University Science Books, 2008.
The last one should be especially good for you, John Roe, because it’s full of estimation problems related to environmental issues, with solutions, and with enough explanation that students can learn the necessary background. Many students will need some help from you, though.
I haven’t read Guesstimation but I have a copy of Guesstimation 2.0. It’s full of fun estimation puzzles.
I plan to pose a lot of these puzzles on Google+ sometime, continuing a series where I posed physics puzzles taken from this book:
• Mark Levi, Why Cats Land on Their Feet: And 76 Other Physical Paradoxes and Puzzles, Princeton U. Press, Princeton, New Jersey, 2012.
Most students who take a math general education course hate math because they hate algebra. The result is that most books intended for a college graduate audience contain no formulas or graphs. For example, The Modern Mind by Peter Watson has a number of chapters on twentieth century science but few equations beyond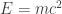 . The students need to be taught to appreciate and understand algebra and its incredible role in the modern world. If I ever were to teach a math for general education course again, I would be tempted to start with the Geometry of Rene Descartes where he showed that the newly perfected, very abstract, field of algebra could be used to easily solve many old problems.
. The students need to be taught to appreciate and understand algebra and its incredible role in the modern world. If I ever were to teach a math for general education course again, I would be tempted to start with the Geometry of Rene Descartes where he showed that the newly perfected, very abstract, field of algebra could be used to easily solve many old problems.
I’m not sure about trying to teach geometry if there’s a limited amount of time for teaching students who may not have the highest levels of motivations. I’d be inclined to try to hit just enough stuff to be give a feeling for important mathematical notions like kinds of functions (linear,quadratic and polynomial, exponential), notions like dynamical systems, equilbrium states, stable equilibria, etc. Even if one can’t (indeed, may not be interested in) doing detailed mathematical proofs, having a good feel for the some of the key ideas in mathematics, particularly applied mathematics.
I’m sure you have heard of Fermi problems, but somebody reading this might not have done. http://en.wikipedia.org/wiki/Fermi_problem
I am reminded of Douglas Hofstader’s article “Number Numbness, or Why Innumeracy May Be Just as Dangerous as Illiteracy.”
There’s a nice program called More or Less on BBC radio 4 which attempts to bring statistics to the masses. Past episodes available here.
http://www.bbc.co.uk/programmes/b006qshd/broadcasts/2012/11
Thanks for all the comments. The Harte book also has a sequel – “Consider a Cylindrical Cow” – but much of the material in it is too sophisticated for the kind of audience that I have in mind. Indeed, I have just started writing some worksheets for the course and it’s clear I am going to have to be pretty ruthless about content.
1) You could always do what is commonly cited as the original Fermi problem: How many piano tuners are there in Chicago?
2) Not appropriate for Measuring but perhaps appropriate for your next topic, “Changing:” Over at OvercomingBias.com, a very important point was just made about how to get significant improvements in Social utility with minimal aggregate reduction in Personal utility. This seems such a massively useful idea to propagate (and one that can be successfully propagated in a class such as you describe) that I can’t resist shoehorning it into this reply.
arch1 wrote:
A precise link, please? Sounds interesting.
URL is http://www.overcomingbias.com/2012/11/marginal-charity.html
My take on the key msg: Many personal choices are exercises in maximizing Private utility as a function of an independent variable. When this also maximizes Social utility, great; when not, this presents (almost by definition) an opportunity to get significant Social utility at little cost in Private utility by moving slightly away from the Private-utility max in the direction of increasing Social utility. Given certain assumptions on the utility curves, the ratio of Social gain to Private loss can be arbitrarily high.
I don’t know why this observation is not more widely trumpeted in e.g. Econ 101 classes. There are obviously caveats to its application, but where applicable it would seem to be a way to further motivate and engage all but the most resolute Scrooges in (on average) furthering the common welfare.
I am not totally sure, if such a course will solve the problems.
In my opinion it is not the problem e.g. that “measuring” is a not well-enough known or used concept. Modern economics is full of seemingly high-level math, which is used to define it as a science, however economists do not even understand the exponential function, otherwise they would not propose unlimited growth or annual growth rates that are only allowed to rise or at least stay constant.
Therefore a campaign should be started to compile all the cases, in which mathematics is abused in one or the other way, mainly on purpose.
If you only tell the people how to calculate or to reason logically, you will exactly get all the brokers and accounting people you now have. People do not have to learn mathematics to make the world a better place, they have to think about ethics. E.g. seeing the humans behind the numbers. People should rather learn to be less confident about their “knowledge”, and instead rather doubt anything, especially if it looks like a numerical fact, which seemingly no one is able to change.
Maybe I got your intention totally wrong, but for me the focus would be on general thinking and questioning autorities in any possible way (yes, professors included) and not to refer to much to a important but nonetheless fashionable subject like “sustainability”, which neglects older and more important problems and is already part of the propaganda e.g. of nuclear power producing companies and the like which are concerned about everything else, but certainly not sustainability.
You should certainly have a look at my namesake (but no relation) David MacKay’s book ‘Sustainable Energy – without the hot air’, available free on-line. Rather than wax purple here I would just note that I’ve said my piece when reviewing it for ‘Physics World’ (with Roger Edgar, ‘Sustainability made simple’).
Niall – Thanks for the reminder about Sustainable Energy Without the Hot Air. I had seen that a year or two ago and it is exactly appropriate.
Wolfgang – I am not sure I am following you correctly, but does this comment from my fourth post address your concern somewhat: “I want to get across two ideas that pull in somewhat different directions: the first that numbers cannot do our judgment (especially our ethical judgment) for us, and the second that they can nevertheless greatly facilitate our judgment by helping us see the moral field clearly. I wonder how possible this will be?”
Yes, somewhat your comment addresses my concerns. I am certainly an advocate for the importance of facts…i.e. mainly numerical information about things. I also think it is a good thing, in general, to teach people a sort of “intuitive” understanding about the significance of things. Not only to measure, but to judge a measurement. To know the dimensions, to judge significance etc. to get used to these sorts of reasoning and thereby “get a feeling” about things. And for this part, there is certainly a need for a better education.
However, and in particular concerning a concept like “sustainability”, there is, in my opinion, nevertheless the danger to overemphasize technicalities. For a mathematician or a natural scientist everything appears to be related by “numbers”, and I personally think in a similar way, but unfortunately it is not like that in reality. Possibly we even learn less about a system the more we understand its numerical properties. Because it is the wrong thing to focus on. Secondly, even if we focus on the numbers, it gets extremely difficult to state the problem correctly. What seems “good” in the first place may have devastating results in its course. E.g. take the production of bioethanol and the resulting increase of food prices in the aftermath. First, it seems to be a good idea to get less dependend from oil. I think no one doubts that this is a finite ressource. And fuel from plants is a nice suistanable idea. It appears like it, at least. But then, bioethanol gets a big business, you can earn more from producing fuel than from selling your crops as food, thereby you destroy things in a more important area, concerning human living. In the end, there a scientific studies that show that even without that consequence bioethanol is not the solution for anything, because mostly its production costs more than it benefits for society are. Because you have to include ALL costs…a thing nearly impossible to estimate for any problem on sustainability. E.g. if you think about it in a very simple way, then nuclear power generation is quite CO2-“neutral”. If you account for the costs for the production of the nuclear fuel and also for the disposal of the radioactive waste it is the worst technology of all. Possibly…the full information needed to state the problem correctly in order to come to a decision about how to act about it is never possible. More numbers will not be more helpful if essential parts of the problem are not even recognized properly. Maybe one could put this in a mathematical way. This would be a great lection.
Here is another example
Yes, nice one. I guess you probably can find a huge number of contradictory examples.
One thing is about assumptions of the theory not being true in reality (such as in the example of partial derivatives), missing terms in the theory etc., the other thing is about “math” that is invented on purpose to alter the effect of some politics in order to favor positive side effects for some small number of people. I guess all the modern financial products are of this kind of math. You want to hide the inferiour quality of your stocks, well bundle them alltogether with a large amount of invented maths, give them some arbitrary acronym, and surely you will find some dumb people to buy them. It is their problem, isn’t it?
Real mathematicians should stand up against this abuse of mathematics, which commonly makes things artificially more complex, just the opposite as it is done in the natural sciences, where all the mathematics ultimately leads to simplification of things (even if in-between things get more difficult). The mathematical theories of stock market are more difficult than any standard model could be, for which reason? Because the stock market is more complex than the universe? I doubt that.
One for the engineers, maybe?
Heard in N. California, from a friend of a friend (no cite, gossip) that commercial solar thermal collectors (hot air/hot water) are being replaced by solar photovoltaic panels, because at current prices that’s cheaper — no plumbing, no tanks, no maintenance, just wires and electric heaters.
Details will be excruciating.
A good spreadsheet-calculator might budge people who haven’t done solar thermal despite its benefit, because of permitting or plumbing concerns.
My local building permit office a year ago wouldn’t let me replace a failing gas water heater with an electric one, because I needed a stronger roof before putting up solar collectors. They figured electric less energy-efficient than gas (losses from the grid) when installed without solar hot water panels. Promises not sufficient.
Now I wonder: solar PV to preheat water?
Electricity can heat water to boiling, unlike solar thermal which can’t heat the tank above the collector temperature. Heck, solar electric could heat a phase change material way hot, if we had one.
“Hybrid PV/Thermal” makes solar cells _more_ efficient by cooling the PV, dumping heat into household water tank — back to plumbing there, but maybe much less plumbing.