There’s a new paper on the arXiv:
• John Baez and Blake Pollard, Quantropy.
Blake is a physics grad student at U. C. Riverside who plans to do his thesis with me.
If you have carefully read all my previous posts on quantropy (Part 1, Part 2 and Part 3), there’s only a little new stuff here. But still, it’s better organized, and less chatty.
And in fact, Blake came up with a lot of new stuff for this paper! He studied the quantropy of the harmonic oscillator, and tweaked the analogy between statistical mechanics and quantum mechanics in an interesting way. Unfortunately, we needed to put a version of this paper on the arXiv by a deadline, and our writeup of this new work wasn’t quite ready (my fault). So, we’ll put that other stuff in a new version—or, I’m thinking now, a separate paper.
But here are two new things.
First, putting this paper on the arXiv had the usual good effect of revealing some existing work on the same topic. Joakim Munkhammar emailed me and pointed out this paper, which is free online:
• Joakim Munkhammar, Canonical relational quantum mechanics from information theory, Electronic Journal of Theoretical Physics 8 (2011), 93–108.
You’ll see it cites Garrett Lisi’s paper and pushes forward in various directions. There seems to be a typo where he writes the path integral
and says
In order to fit the purpose Lisi concluded that the Lagrange multiplier value
In similarity with Lisi’s approach we shall also assume that the arbitrary scaling-part of the constant
is in fact

I’m pretty sure he means given what he writes later. However, he speaks of ‘maximizing entropy’, which is not quite right for a complex-valued quantity; Blake and I prefer to give this new quantity a new name, and speak of ‘finding a stationary point of quantropy’.
But in a way these are small issues; being a mathematician, I’m more quick to spot tiny technical defects than to absorb significant new ideas, and it will take a while to really understand Munkhammar’s paper.
Second, while writing our paper, Blake and I noticed another similarity between the partition function of a classical ideal gas and the partition function of a quantum free particle. Both are given by an integral like this:
where is a quadratic function of
Here
is the number of degrees of freedom for the particles in the ideal gas, or the number of time steps for a free particle on a line (where we are discretizing time). The only big difference is that
for the ideal gas, but
for the free particle.
In both cases there’s an ambiguity in the answer! The reason is that to do this integral, we need to pick a measure The obvious guess is Lebesgue measure
on But this can’t be right, on physical grounds!
The reason is that the partition function needs to be dimensionless, but
has units. To correct this, we need to divide
by some dimensionful quantity to get
In the case of the ideal gas, this dimensionful quantity involves the ‘thermal de Broglie wavelength’ of the particles in the gas. And this brings Planck’s constant into the game, even though we’re not doing quantum mechanics: we’re studying the statistical mechanics of a classical ideal gas!
That’s weird and interesting. It’s not the only place where we see that classical statistical mechanics is incomplete or inconsistent, and we need to introduce some ideas from quantum physics to get sensible answers. The most famous one is the ultraviolet catastrophe. What are all rest?
In the case of the free particle, we need to divide by a quantity with dimensions of lengthn to make
dimensionless, since each has dimensions of length. The easiest way is to introduce a length scale
and divide each
by that. This is commonly done when people study the free particle. This length scale drops out of the final answer for the questions people usually care about… but not for the quantropy.
Similarly, Planck’s constant drops out of the final answer for some questions about the classical ideal gas, but not for its entropy!
So there’s an interesting question here, about what this new length scale means, if anything. One might argue that quantropy is a bad idea, and the need for this new length scale to make it unambiguous is just proof of that. However, the mathematical analogy to quantum mechanics is so precise that I think it’s worth going a bit further out on this limb, and thinking a bit more about what’s going on.
Some weird sort of déjà vu phenomenon seems to be going on. Once upon a time, people tried to calculate the partition functions of classical systems. They discovered they were infinite or ambiguous until they introduced Planck’s constant, and eventually quantum mechanics. Then Feynman introduced the path integral approach to quantum mechanics. In this approach one is again computing partition functions, but now with a new meaning, and with complex rather than real exponentials. But these partition functions are again infinite or ambiguous… for very similar mathematical reasons! And at least in some cases, we can remove the ambiguity using the same trick as before: introducing a new constant. But then… what?
Are we stuck in an infinite loop here? What, if anything, is the meaning of this ‘second Planck’s constant’? Does this have anything to do with second quantization? (I don’t see how, but I can’t resist asking.)

There seems to be a typo in your typo:
There seems to be a typo where he writes the path integral
Formula does not parse
and another here:
Both are given by an integral like this:
Formula does not parse
where $S$
and finally here:
Does this have anything to do with <a href ="http://en.wikipedia.org/wiki/Second_quantization" second quantization?
Sorry. Never mind. They all seem good now. Not sure what happened there…
I fixed them as soon as I saw the article I’d posted… but not before you! You’re too quick!
So why does the partition function have to be dimensionless? Why not regard it as a quantity of dimension lengthn? For example, consider the probability that the system is at a certain position
have to be dimensionless? Why not regard it as a quantity of dimension lengthn? For example, consider the probability that the system is at a certain position  ,
,
This should be a probability density, and hence
should be a probability density, and hence  better have dimension lengthn!
better have dimension lengthn!
Also, equations like
still make sense with dimensionful . So what’s the problem with this?
. So what’s the problem with this?
Apologies if this has already been discussed elsewhere; I haven’t seen it explained in the paper.
Good question! There are two slightly different questions: does need to be dimensionless in statistical mechanics, and does it need to be so in quantum mechanics.
need to be dimensionless in statistical mechanics, and does it need to be so in quantum mechanics.
In statistical mechanics everyone seem to agree that should be dimensionless. For example, the free energy is
should be dimensionless. For example, the free energy is
where is temperature and
is temperature and  is Boltzmann’s constant.
is Boltzmann’s constant.  has dimensions of energy so
has dimensions of energy so  should be dimensionless, which means that
should be dimensionless, which means that  is dimensionless.
is dimensionless.
Indeed, the usual rules give no consistent way of assigning dimensions to unless
unless  is dimensionless. You cleverly note that the derivative of
is dimensionless. You cleverly note that the derivative of  can still make dimensional sense, but in statistical mechanics we also really care about
can still make dimensional sense, but in statistical mechanics we also really care about  itself.
itself.
(By the way, in the paper we use a system where temperature has units of energy and This doesn’t affect the conclusions here.)
This doesn’t affect the conclusions here.)
In quantum mechanics we could, I suppose, argue that the ‘free action’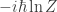 is not physically interesting so we don’t need
is not physically interesting so we don’t need  to make dimensional sense. But instead, we are hoping that the whole analogy between stat mech and quant mech works as seamlessly as possible. So for us, the same argument that forced
to make dimensional sense. But instead, we are hoping that the whole analogy between stat mech and quant mech works as seamlessly as possible. So for us, the same argument that forced  to be dimensionless in stat mech also applies to quant mech.
to be dimensionless in stat mech also applies to quant mech.
I’ll have to think about this when I have some more time. It sounds like you have me trapped, but I will try to escape… or at least try to figure out what’s going on. Thanks!
Aha! So if I hypothetically used a dimensionful partition function and had a value of e.g. , the free energy would end up being
, the free energy would end up being
which indeed seems odd — since what could taking the logarithm of a unit possibly mean? On the other hand, the second term is like a choice of zero for . Since observable quantities typically (or always?) involve only free energy differences, this choice of zero doesn’t have observational consequences.
. Since observable quantities typically (or always?) involve only free energy differences, this choice of zero doesn’t have observational consequences.
That’s a reasonable argument and maybe it’s true in some fundamental sense. However, when people compute the free energy of a classical ideal gas. they actually want to know the answer ‘on the nose’, not just up to a constant. The reason, perhaps, is that in this subject everyone assumes that the free energy of a box full of vacuum is zero. So a zero of energy has already been fixed.
The calculation turns out to be very interesting. You can see one version here:
• S. M. Tan, Statistical Physics, Chapter 4: the Classical Ideal Gas.
where the final answer is in equation (4.31). One strange thing about this particular version of the calculation is that it starts as a quantum calculation and then takes the classical limit. You will see that the volume of the box divided by the ‘thermal DeBroglie wavelength’ of the gas molecules shows up in the answer—see eq. (4.36) for an explanation of what I mean.
Thus, the answer involves Planck’s constant, even in the classical limit!
You can also try to compute the free energy of the classical ideal gas purely using classical mechanics. People must have tried this before quantum mechanics was invented. This is closer to what we’re talking about here. In this you naively start by computing
where describes the momentum of
describes the momentum of  particles in a 3-dimensional box
particles in a 3-dimensional box 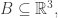
 describes the position of those particles, and
describes the position of those particles, and 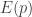 is the kinetic energy of those particles, a quadratic function of
is the kinetic energy of those particles, a quadratic function of  .
.
However, this formula for is ‘wrong’, because
is ‘wrong’, because  is not dimensionless! It has units of momentum times position to the nth power: that is, action to the nth power. To make it dimensionless we need to divide the measure
is not dimensionless! It has units of momentum times position to the nth power: that is, action to the nth power. To make it dimensionless we need to divide the measure
by something with units of action to the nth power… and this is where Planck’s constant, or more precisely shows up! In this approach, it enters in a somewhat ad hoc way.
shows up! In this approach, it enters in a somewhat ad hoc way.
In other words, we’re seeing that to compute the free energy of a classical ideal gas ‘on the nose’, not just up to a constant, we’re forced to introduce a quantity with dimensions of action. This quantity later turns out to equal Planck’s constant.
So, we’re seeing a way that quantum mechanics pushes its nose under the door even when you didn’t invite it, like a camel that you wish would stay outside your tent.
Tobias wrote:
I want to more clearly admit that to a large extent this must be the right answer to the puzzle.
In statistical mechanics, adding a constant to the Hamiltonian doesn’t change the probability of being in any state. It multiplies the partition function by a constant. It adds a constant to the free energy. But for most purposes, it should be considered as a kind of ‘gauge transformation’ – a symmetry that doesn’t affect anything we can measure.
Similarly, in the path integral approach to quantum mechanics, adding a constant to the action doesn’t change the amplitude of any history. It multiplies the partition function by a constant. It adds a constant to the free action. But for most purposes, it should be considered as a kind of ‘gauge transformation’.
Nonetheless, in statistical mechanics there are some situations where people want a specific answer for the free energy, not just ‘up to a constant’. To get this, it seems we need to introduce some ideas from quantum statistical mechanics. This has the effect of introducing Planck’s constant, which allows us to make the partition function dimensionless and also (it seems) choose a specific ‘correct value’ for it!
Similarly—following the analogy I’m always using here—there could be some situations in quantum mechanics where we want a specific answer for the free action, not just ‘up to a constant’. To get this, it seems we need to introduce some ideas from… some new subject! This has the effect—at least in the example Blake and I looked at in our paper—of introducing a fundamental length scale, which allows us to make the partition function dimensionless and also choose a specific value for it.
I want to think about this more, even if it’s rather peculiar. Pushing analogies until they break is often interesting.
(Naturally the idea of choosing a fundamental length scale makes me think of quantum gravity and the Planck length. Could quantum gravity solve some problems of quantum mechanics just as quantum mechanics solved some problems of statistical mechanics? This is a somewhat far-out idea. I’m not claiming it makes sense. But I want to be the first to mention it, just in case it turns out to be brilliant instead of stupid.)
It is very, very, interesting.
In statistical mechanics (canonical and grand canonical) the partition function is evaluated using the number of quantum states of simple system (for example particles confined in a box, or quantum harmonic oscillator), with the volume of each distinct quantum state.
If there is an analogy here, then there is a number of trajectory between initial state and final state, that can give the correct partition function.
I am thinking two possibility.
The first (improbable) is a simple constrain on the possible trajectories, for example optical fibers (for photons), or multiple slits (for particles), to reduce the number of the trajectories.
The second is a particle in a box experiment, where a single particle spread in the initial box, and after a slow septum movement until a final state: if it possible to calculate the number of trajectories between the initial state and the final state, then it is possible to evaluate the correct partition function for this system (denominator of Z); I am thinking that if the movement is slow (momentum constraint), the trajectory is unique, when the movement is quick, the number of trajectory grow.
If exist a quantum partition function, then exist a number of trajectories for each volume in the phase space (constraint on the possible trajectories), and it is the first time that read something like this.
Thanks! So abstractly, maybe there is a sense in which a Hamiltonian or action actually takes values not in the real numbers, but in an affine line. And likewise for the free energy. I’m quite confused about what to make of this, though…
In general, I find it important to stress that there is no consistency problem with classical statistical mechanics without quantum theory. Physicists often seem confused about this kind of issue and summon one theory to the “rescue” of another, even if the latter is perfectly consistent. I wonder if this applies e.g. to Bohr’s general relativity argument in the Bohr-Einstein debates, but this is a can of worms that I’d rather keep closed.
Tobias wrote:
As an abstract general framework it’s consistent and also extremely powerful. However, there are some important classical Hamiltonians on infinite-dimensional vector spaces
on infinite-dimensional vector spaces  for which
for which
is ill-defined, yet the corresponding quantized analogue
is well-defined. Namely, the Hamiltonian for a box of electromagnetic radiation. This is the ultraviolet catastrophe, and this is how Planck stumbled into quantum mechanics. My point now is that even in situations where the integral is well-defined, sometimes it’s not dimensionless until we divide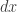 by a power of
by a power of 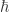 , or some arbitrarily chosen constant with units of action.
, or some arbitrarily chosen constant with units of action.
Physicists have psychological reasons for wanting to find ways that new theories can ‘save’ old ones, instead of continuing to pursue the old ones as self-contained self-consistent objects of study. They get paid for discovering new theories.
Excuse me, there was an overlapping of the two definitions, while writing.
I write the quantum partition function for path integral like analogy.
If exist a path integral (that have an analog form with a partition function), then exist a number of trajectories for each volume in the phase space (constraint on the possible trajectories), and it is the first time that read something like this.
By “it” I think you mean the length scale. Can you elaborate on how this allows you to choose a specific value for it? I don’t see why, in the pure classical case, it’s insufficient to just choose an arbitrary value for it.
John wrote:
Bruce wrote:
No, I meant the partition function.
It might be helpful to recall the more familiar but completely analogous situation in statistical mechanics, where we need to choose a quantity with dimensions of action to make the partition function dimensionless, and also give the partition function a specific value.
dimensionless, and also give the partition function a specific value.
This is important, for example, when we try to compute the free energy of a classical ideal gas, which is
If we only know the partition function up to a constant multiple, we only know the free energy up to an additive constant. And if a quantity isn’t dimensionless, it’s usually considered bad to take its logarithm (though Tobias has argued above that it can be okay).
Earlier I wrote:
Right — I understand this part:
But in the absence of any desire to go beyond the classical situation, I don’t get this part:
That is, sticking to classical ideas, I don’t see why that “quantity with dimensions of action” can’t have an arbitrary value.
Bruce wrote:
Yes, it can have any value you want. But its value affects the free energy you compute for the classical ideal gas. If you want to get the “right answer”—the answer we now believe to be close to the answer for an actual gas—you need to pick this quantity with dimensions of action to be Planck’s constant.
But suppose we didn’t have quantum mechanics! Would we be in serious trouble?
Probably not. Since only energy differences are measurable, one can argue—as Tobias did earlier in this long conversation, that an additive constant ambiguity in our definition of free energy doesn’t affect any physical predictions. That sounds correct to me.
But there’s more. The ambiguity also affects the entropy you compute for the classical ideal gas! This is more surprising, because—at least nowadays—we’re less likely to think of entropy as being defined only up to an additive constant.
But in fact, if you try to measure the entropy of a substance (as opposed to computing it), you’ll see that we typically fix this constant using the Third Law of Thermodynamics:
The entropy of a perfect crystal at absolute zero is exactly equal to zero.
So, we measure the entropy of a gas at a given temperature by first chilling it down to absolute zero, or close, and then keeping careful track of how much heat energy it takes to warm it up to the given temperature. If we can’t afford to do this experiment, entropy is defined only up to a constant.
(And indeed, we can never afford to get all the way down to absolute zero: we have to hope that close is good enough.)
But a classical ideal gas never freezes and forms a crystal! I believe its entropy just keeps dropping more and more as we go closer and closer to absolute zero! More precisely, it goes to : at low temperatures it goes roughly like
: at low temperatures it goes roughly like  , up to some fudge factors.
, up to some fudge factors.
In short, the free energy and energy of a classical ideal gas are ambiguous up to additive constants, and the latter behaves in a rather annoying way. If there were no quantum mechanics we could learn to live with this, but in fact physicists were irritated by this problem until quantum mechanics came along.
I found this article quite helpful:
• S. M. Tan, Statistical Physics, Chapter 4: the Classical Ideal Gas.
though they should have come out and said what I just said.
The problem with the units of Z comes from dimensionally invalid formula for differential entropy used in obtaining Gibbs-Boltzmann distribution. instead of integrating p(q)log(q) one should calculate p(q)log(p(q)/m(q)) – where m(q) is a “base measure” i.e dq^n – thus dimensionful. After solving the optimization problem the base measure will appear in the numerator…
Typo on p. 2: “The kinetic energy is often, though not always, has a minimum at velocity zero.” And p. 15: “In the subject of computation, there is a superficiallly different notion”.
Thanks, damn you!
In the approach that you took, the is a path density function? How does this approach differ from Maximum caliber?
is a path density function? How does this approach differ from Maximum caliber?
Bit confused later on (page 6) how can the path density not be conserved?
There is a similarity in what you do here to how Gibbs derived the index of probability, using Gibbs notation. The index of probability is defined as
is defined as 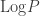 where
where  is the coefficient of probability, a conserved quantity, from the conservation of the density in phase (continuity).
is the coefficient of probability, a conserved quantity, from the conservation of the density in phase (continuity).
Gibbs then did a first order expansion and arrived at the canonical distribution, where
and arrived at the canonical distribution, where 
Where I am confused (This is due to my ignorance) is that the partition function, at least how Gibbs defines it in Chapter 8 seems to be a means of converting from the internal coordinate system to that of energy alone. Can this approach be applied to what you are doing here?
Also, the modulus of the the action paths is constant, ? Why would the variability of paths be fixed? Here I am really showing my ignorance…
? Why would the variability of paths be fixed? Here I am really showing my ignorance…
Thank you for your patience and your interesting paper.
While the paper sounds very interesting, I must say that the lead-off “There’s a new paper on the arXiv” sounds less than newsworthy.
Yes. That was a joke.
Or so you claim now, after having a chance to go back and count the number of other papers that appeared this week.
Claude Shannon showed entropy is a measure of information. Information sources quantum mechanics, arxiv.org:1208.0493. Perhaps entropy measures are default quantized.
View at Medium.com
Is there a Noetherean symmetry enforcing conservation of information?
Just to chase the analogy from the other end, the ultraviolet catastrophe can be read: supposing one initially has a classical field oscilating with finite energy, and a stochastic process redistributing that energy among the field modes at random and in a suitably conservative and symmetric and transitive way; then the bandwidth of the system will tend to infinity in a particular, central-limit-theorem kind of way (even while the signal strength in any subband tends to zero).
From the fourier-dual point of view of resolution, that means the discernible features of the oscilating field will tend towards very small size. And this is (when I get sloppy and provocative all at once) amusingly like what we see in the observable universe: the discernible structures (galaxy local groups etc.) are getting smaller when compared to the universe-as-a-whole — although we usually say it the other way around, that the observable universe is stretching apart.
Sorry for this very basic question, but I don’t really understand the analogy , basically because I don’t see how
, basically because I don’t see how  is a variable.
is a variable.
Why isn’t a constant?
a constant?
Of course is a constant. But when you write down formulas in quantum mechanics involving
is a constant. But when you write down formulas in quantum mechanics involving  you can treat it as a variable. This is widely done. For example, people study the ‘classical limit’ of quantum mechanics by doing calculations that include
you can treat it as a variable. This is widely done. For example, people study the ‘classical limit’ of quantum mechanics by doing calculations that include 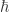 and then taking the limit
and then taking the limit 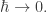 Then you get back to classical mechanics.
Then you get back to classical mechanics.
A more refined version of this idea gives the ‘loop expansion’ in quantum field theory. We write answers to physical questions as power series in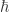 , and we find the coefficients of these power series in the usual way, using Taylor series: treating the answer as a function of
, and we find the coefficients of these power series in the usual way, using Taylor series: treating the answer as a function of 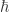 and repeatedly differentiating it!
and repeatedly differentiating it!
In short: it works, and it’s illuminating. So, it’s good to do, even if it raises questions we can’t answer yet. That’s often the case in physics.
However, it would be nice to understand this mystery better. Maybe we could improve the analogy between statistical mechanics and quantum mechanics by making analogous to something we can actually adjust in the lab!
analogous to something we can actually adjust in the lab!
In our next paper Blake and I hope to do that. We were going to include this in our first paper, but it turned out to be harder than we thought.
Congratulations to you and Blake on getting this paper out! Good to see this stuff getting more attention.
There is an issue troubling me though. In your post, you criticize Joakim Munkhammar for referring to quantropy incorrectly as entropy, because it is complex. And, more seriously, in your paper, you choose to refer to the “amplitude”, — but, in calculations, such as at the bottom of p5, you use it not as an amplitude but as a probability density. This clearly troubles you too, since, on the following line, you admit it’s “a bit odd.” But I think it’s worse than a bit odd, I think it’s terribly wrong to refer to
— but, in calculations, such as at the bottom of p5, you use it not as an amplitude but as a probability density. This clearly troubles you too, since, on the following line, you admit it’s “a bit odd.” But I think it’s worse than a bit odd, I think it’s terribly wrong to refer to  as “amplitude,” because that has a different and very strong meaning to physicists, implying
as “amplitude,” because that has a different and very strong meaning to physicists, implying  , which you do not mean.
, which you do not mean.
I realize this may seem like bandying about over what we call things, but it’s obscuring a potentially fascinating subject. What we are doing here is generalizing to complex probabilities, and using that to derive QM. The relevant quote, I think from Hadamard, is “The shortest path between two truths in the real domain often passes through the complex domain.” You and Blake are, perhaps wisely, being hesitant about tackling anything as crazy as complex probability. But I think that does need to happen here, and tiptoeing around the issue will sadly delay the fun.
Axioms for possibility and impossibility
(Information and Impossibilities, Jon Barwise, Notre Dame J. Formal Logic Volume 38, Number 4 (1997), 488-515.)
What kind of numbers would mean “possibility”?
Something is either possible or it’s not, so it seems no possibility could rationally be compared to any other by a “greater-than” “less than” relation. Every one of them just is a possibility or is not. There is no half-way point in being a possibility.
Then for example there’s the possibility of my being in the universe, it just depends on me being alive or not. Next imagine a divided universe, with part A and part B. The possibility of me being in the universe could then be either (a) the possibility of being in part A or (b) the possibility of being in part B. In the case where I make the A part of the universe vanish, the possibility that I’m in the universe is then just the possibility that I will be in part B. And vice versa.
thePossibilityOfBeingInTheUniverse = A + B = B + A = thePossibilityOfBeingInTheUniverse
Possibility seems to be that kind of number.
But I also experience possibility in another way. Say that I’m planning a BBQ, and I want to invite Homer. But Homer hates, I mean hates, to BBQ in the rain. So initially in my plans for the party, I consider for planning purposes the conjunction of two possibilities: (a) the possibility it will rain “R” and (b) the possibility that Homer will come “H”. If both possibilities occur we have to move the party into the garage as quickly as possible, to avoid Homer’s whining. But if either possibility vanishes, my worry about quickly moving the party into the garage vanishes. It doesn’t matter which possibility I think of first.
thePossibilityOfUsingGarage = R*H = H*R = thePossibilityOfUsingGarage
So possibility must be this kind of number as well.
I’ve also had another kind of experience. Say that Homer suddenly turns into a complete ass, which is not an unusual experience for him. I quickly factor out any consideration I once had at all for Homer’s baby man worries about the rain. I factor that consideration completely out from my planning process, and what the hell, if it rains, it rains and we’ll think of something. That’s part of the fun down here in the islands!
BEFORE:
ScopeOfPlanning: thePossibilityOfUsingGarage = R*H
AFTER:
ScopeOfPlanning: thePossibilityOfUsingGarage/H = R
Factoring away from the possibility of using the garage any consideration of the possibility that Homer will attend results in me only considering only the possibility it will rain, and heck I think that’s part of the fun. Sort of an adaptive team exercise, especially in the islands.
This narrows down the suspects. The kind of number that means “possibility” must be one of the four kinds of numbers that are in the division algebras. Check it out- the above constraints mean a complex number means possibility, and if it vanishes so does the possibility…
?
Garrett wrote, modulo tiny changes in notation:
I’m not being hesitant. I think is an amplitude.
is an amplitude.
When you use the path integral approach to compute the wavefunction for a particle that starts at a specific position
for a particle that starts at a specific position 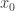 at a specific time
at a specific time 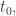 you integrate
you integrate  over all paths starting at
over all paths starting at 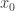 at time
at time 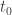 and ending at
and ending at  at time
at time 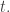 You can then prove that
You can then prove that  obeys Schrödinger’s equation.
obeys Schrödinger’s equation.
Since is an amplitude, I claim that
is an amplitude, I claim that  should also be considered an amplitude.
should also be considered an amplitude.
Then we can say: to figure out the amplitude for a particle to get somewhere, we work out the amplitude that it takes any specific path, and then integrate that over all paths that get there.
In a double slit experiment, we see constructive and destructive interference effects, thanks to the fact that these numbers are complex.
are complex.
I think what I’m saying fits quite nicely with how Feynman explained path integrals, and how physicists use them.
There’s more to say, but this is enough to get the conversation going.
Well, yes, that establishes that is related to an amplitude,
is related to an amplitude, 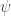 , but IS
, but IS  an amplitude? I’m not sure of this, but I think
an amplitude? I’m not sure of this, but I think  is always used as a probability. It’s normalized as a probability:
is always used as a probability. It’s normalized as a probability:
And it’s used to compute expected values as a probability:
$latex = \int_X a A dx $
For to be a probability amplitude, and not a probability, I think it’s necessary that it be used to compute a probability as
to be a probability amplitude, and not a probability, I think it’s necessary that it be used to compute a probability as  . Is this ever the case?
. Is this ever the case?
Maybe we need a new word for a generalized probability that can be complex?
I figure: if the complex number associated to a path
associated to a path  were a probability density and we integrated it over the set of paths from one spacetime point to another, we’d get the probability of going from the first point to the second. But we don’t: we get the amplitude of going from the first point to the second. So I feel fine calling
were a probability density and we integrated it over the set of paths from one spacetime point to another, we’d get the probability of going from the first point to the second. But we don’t: we get the amplitude of going from the first point to the second. So I feel fine calling  an amplitude density, or amplitude for short.
an amplitude density, or amplitude for short.
I don’t mind you calling it a complex probability, though.
I completely agree that there’s something remarkable about how we normalize , not by requiring that the integral of
, not by requiring that the integral of 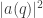 equal 1, but by requiring that the integral of
equal 1, but by requiring that the integral of  equal 1.
equal 1.
This is something I want to understand. Of course this is needed for Wick rotation—the replacement of time by imaginary time, reinterpreted as times inverse temperature—to relate amplitudes in quantum mechanics to probabilities statistical mechanics. But I want to understand the ‘deep inner meaning’ of Wick rotation. That’s what this ‘quantropy’ work is about.
times inverse temperature—to relate amplitudes in quantum mechanics to probabilities statistical mechanics. But I want to understand the ‘deep inner meaning’ of Wick rotation. That’s what this ‘quantropy’ work is about.
I don’t think that deciding what to call is important to me. When we understand what’s going on, the terminology may fall into place. There are some things Blake is starting to do that I’m hoping will make real progress. And the stuff we’ve done so far opens up lots of new questions—like the one mentioned in this blog article, the need for a new dimensionful parameter, analogous to Planck’s constant, to make the partition function
is important to me. When we understand what’s going on, the terminology may fall into place. There are some things Blake is starting to do that I’m hoping will make real progress. And the stuff we’ve done so far opens up lots of new questions—like the one mentioned in this blog article, the need for a new dimensionful parameter, analogous to Planck’s constant, to make the partition function  dimensionless.
dimensionless.
When you integrate over paths that go from a first spacetime point to a second, you get an amplitude,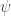 , because you have manifestly instituted time ordering. An amplitude is half a probability (or, somewhat more accurately, a square root). To maintain reversal symmetry, you need also include paths from the second point to a third. Combining these amplitudes gives a probability,
, because you have manifestly instituted time ordering. An amplitude is half a probability (or, somewhat more accurately, a square root). To maintain reversal symmetry, you need also include paths from the second point to a third. Combining these amplitudes gives a probability,  . Amplitudes come from factoring probability in this way. And what you are calling
. Amplitudes come from factoring probability in this way. And what you are calling  is a probability and not an amplitude.
is a probability and not an amplitude.
Garrett wrote:
I’m not sure what you mean by that. In my previous comment, when I integrated over all paths
over all paths  with endpoints
with endpoints  and
and 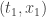 , I said the result was the amplitude for a particle that starts at the spacetime point
, I said the result was the amplitude for a particle that starts at the spacetime point  to end up at
to end up at 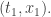 But it’s also the amplitude for a particle that ends up at the point
But it’s also the amplitude for a particle that ends up at the point  to start at
to start at 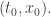 It’s only my language—“starts at”, “ends up at”—that breaks time reversal symmetry. And I’m only talking that way because that’s how people tend to talk. If
It’s only my language—“starts at”, “ends up at”—that breaks time reversal symmetry. And I’m only talking that way because that’s how people tend to talk. If  we say the particle “starts at”
we say the particle “starts at”  and “ends up at”
and “ends up at” 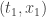 , but I don’t need to assume
, but I don’t need to assume  and I don’t need to talk in a time-asymmetric way.
and I don’t need to talk in a time-asymmetric way.
I don’t know about this “you need” business. But I’m perfectly happy to consider this other setup if it helps shed light on the relation between probabilities and amplitudes.
It sounds interesting, but it’s not shedding light for me yet. Let me try to understand what you’re saying. Say I have three spacetime points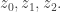 I let
I let  be the integral of
be the integral of  over all paths with endpoints
over all paths with endpoints 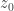 and
and  I let
I let 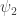 be the integral of
be the integral of  over all paths with endpoints
over all paths with endpoints  and
and  I multiply
I multiply  and
and  or maybe
or maybe  and
and  What does this mean? You seem to be saying it’s a probability.
What does this mean? You seem to be saying it’s a probability.
I think that if then what I’m calling
then what I’m calling 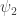 will often equal
will often equal  , so that
, so that
is the probability of a particle starting at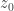 reaching
reaching 
I don’t feel a strong sense of enlightenment yet. In particular I’m not sure why you mentioned a ‘third point’ if this third one is the first one.
Repeatedly saying this isn’t going to speed up information transmission between us. It’s very unlikely that after saying this four times, saying it a fifth time will teach me anything. I heard you say it each time.
Ha, sorry, I’ll make an effort to be less sphexish. This is what I meant, more precisely, about the probability factoring:
in which
The quantum wavefunction,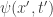 , is the amplitude for paths with
, is the amplitude for paths with  leaving from
leaving from  — these amplitudes multiply to give the probability of the system passing through
— these amplitudes multiply to give the probability of the system passing through  . This should also work if we presume other, possibly identical, start and end points. And it requires a time-independent Lagrangian.
. This should also work if we presume other, possibly identical, start and end points. And it requires a time-independent Lagrangian.
It took me quite a while to fix the LaTeX on your comment. The problem turned out to be that you used
’
instead of
‘
in various places. These are different characters and only the latter is digestible by LaTeX here. After I recover I’ll think about what you actually said.
Thank you! I tested it through my LaTeX compiler and it worked, so I was sad to see the errors here. Comment preview would be good. Or maybe there’s a sandbox?
Comment preview would be good, but so far I’ve been too lazy to pay the money to get these extra features. Sorry.
You can use my blog as a sandbox if you want, e.g. the “About” page; I’ll just delete stuff after a while.
I also don’t mind fixing people’s TeX; I just mentioned your case because the bug was fiendishly subtle.
You had to do something a bit unusual to put right single quote marks in two different fonts in your comment. If I type x’, everything is fine in TeX here: it gives
You did that most of the time, but your comment also had some instances of the fancy curly quote
’
which I can’t type. I can only cut-and-paste it. If I use that and put x’ in TeX it gives
So, whatever weird thing you did, don’t.
garrett says:
17 November, 2013 at 12:55 pm
(If not I wonder: are we seeing a subtle physical distinction?)
John Baez says:
17 November, 2013 at 5:36 pm
I can think of two games, one called probability learning from the Handbook of Experimental Economics, the other a kind of iterated shell game, where in both cases these formulas hold–
Where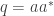 as in then Born rule, this equation is an equilibrium law constraining certain kinds of entropic force in mathematical games (as Professor Baez showed in a previous post).
as in then Born rule, this equation is an equilibrium law constraining certain kinds of entropic force in mathematical games (as Professor Baez showed in a previous post).
It is called Born’s Rule if But in these games it’s a law governing an equilibrium between two opposing entropic forces, a game whose result is the Rule. Neither force can destroy the other, and due to finite situations where the iterated games can be counted by finite integers, the observed percentage rates which result dither around the above law of probability learning.
But in these games it’s a law governing an equilibrium between two opposing entropic forces, a game whose result is the Rule. Neither force can destroy the other, and due to finite situations where the iterated games can be counted by finite integers, the observed percentage rates which result dither around the above law of probability learning.
In a category where it’s not the case that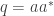 , it would be unthinkable to play these games.
, it would be unthinkable to play these games.
John…I believe from some time ago, that if duality is implemented at the level your analogies seem to point out, the “new” Planck constant should be related to the MAXimum action, and not to the minimum action (that is the first Planck’s constant)…
Hi there,
A couple questions concerning some points that are confusing me:
1. As discussed elsewhere (http://en.wikipedia.org/wiki/Path_integral_formulation) the complex partition function Z defined in the context of ‘quantropy’ discussed here seems to be exactly the quantum propagator K. Given that this is true the propagator is known exactly (see for example Hagen Kleinert’s book) for a variety of systems including the free particle, harmonic oscillator, the hydrogen atom etc. Yet, Z discussed here for the free particle doesn’t seem to correspond to the propagator for the free particle. Am I mistaken then that the complex Z discussed here is not in fact identical to the propagator?
On a related note,
2. The dimensionful constant used in calculating Z seems to be identical to the normalization constant used for the Gaussian integrations used in calculations for exact propagators. It turns out that the later normalization constants, when generalized to higher dimensional systems and or considerations of the relativistic particle on a curved manifold, are related to the Van Vleck determinant which in turn relates to the semi classical approximation and the Hamilton Jacobi equation. So, am I also mistaken that the normalization constants discussed here are in equivalent?
used in calculating Z seems to be identical to the normalization constant used for the Gaussian integrations used in calculations for exact propagators. It turns out that the later normalization constants, when generalized to higher dimensional systems and or considerations of the relativistic particle on a curved manifold, are related to the Van Vleck determinant which in turn relates to the semi classical approximation and the Hamilton Jacobi equation. So, am I also mistaken that the normalization constants discussed here are in equivalent?
Thanks ahead of time for clarification of these points!
Cheers,
Scott
Hi! I’m grading homeworks, so I’ll answer your first question now and tackle the second one when I need another break.
The partition function we discuss is not the propagator.
The partition function is, in principle, the integral of the exponentiated action
is, in principle, the integral of the exponentiated action
over all paths that start at some time
that start at some time 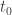 and end at some time
and end at some time 
The propagator is the integral of the exponentiated action over all paths that start at position
is the integral of the exponentiated action over all paths that start at position 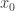 at time
at time 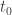 and end at position
and end at position 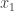 at time
at time 
When I say ‘in principle’, it’s for this reason. In our paper we study the partition function of a free particle. This has space translation symmetry: if you push a path 2 meters to the right it has the same action. So, if you integrate over all paths that start at some time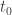 and end at some time
and end at some time  you get infinity.
you get infinity.
To deal with this, we use a standard trick called ‘gauge-fixing’. This means that we only integrate over paths that start at some fixed position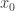 at time
at time 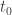 .
.
This makes the partition function look more like the propagator than it really should! The only difference now is that in the partition function we let the path end at whatever position it wants at time while in the propagator we make it end at the position
while in the propagator we make it end at the position 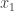 .
.
If we were studying the harmonic oscillator, we would not need to do this gauge-fixing. Blake is working on that case now, and I hope we’ll talk about it soon.
In any event, the partition function can be obtained from the propagator by doing a further integral: integrating over the allowed endpoints of the path.
Hi there,
Thanks for the clarification!
So, the partition function is the propagator integrated over all future end points;
which explains why they appear so similar to functional integrals! Further, given the exact expressions known for for various systems; it shouldn’t be difficult to calculate the complex partition function for those systems.
for various systems; it shouldn’t be difficult to calculate the complex partition function for those systems.
In terms of the more I looked at things it seems (although I could be mistaken) that this is Feynman’s ‘proportionality factor’. In the folklore, Dirac’s original paper postulated that the short time propagator ‘goes like’
the more I looked at things it seems (although I could be mistaken) that this is Feynman’s ‘proportionality factor’. In the folklore, Dirac’s original paper postulated that the short time propagator ‘goes like’
Feynman and Herbert Jehle supposedly considered this in a bar one night and discussed what ‘goes like’ could mean? The next day Feynman realized, by mental gymnastics, that in order for this to agree with Schrödinger’s equation in the limit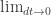 ‘goes like’ really means ‘is proportional to’. The constant of proportionality being
‘goes like’ really means ‘is proportional to’. The constant of proportionality being
in the case of the free particle in one dimension. Here, the path integral is written
If I am not mistaken is required to make the short time propagator satisfy the heat kernel initial condition
is required to make the short time propagator satisfy the heat kernel initial condition
Cheers,
Scott
Where did you read this story about Feynman and Jehle? And where did you read about Feynman’s ‘proportionality factor’. I’d like to read more about the history of these ideas, because it might contain some useful clues. Embarrassingly, I don’t know Feynman and Hibbs book on path integrals very well.
Looking it up in Gleick’s biography, I found that Feynman tells the story in his Nobel lecture.
Hi there,
Sorry about the ‘dog’s breakfast’ I made with my LaTex; thanks for making various corrections!
Feynman discusses in his Nobel lecture (http://www.nobelprize.org/nobel_prizes/physics/laureates/1965/feynman-lecture.html) how Jehle pointed out Dirac’s paper concerning the role of the classical action when they were at a beer party at the Nassau Tavern in Princeton. This is also described in more detail in Gleick’s book ‘Genius’, Silvan’s Schweber’s book ‘QED and the Men Who Made it: Dyson, Feynman, Schwinger and Tomonaga’ (and other papers http://www.rpgroup.caltech.edu/courses/aph105c/2006/articles/Schweber1986.pdf).
Cheers,
Scott
Discussion of the proportionality factor, as it figures in establishing the path integral as a solution of Schrodinger’s equation, can be found in Feynman and Hibbs or Kleinert’s books. Peskin and Schroeder’s ‘Intro to QFT’ and Zinn Justin’s ‘QFT and Critical Phenomena’ also show the derivation.
An online discussion (by Zinn Justin) is also available at scholarpedia (http://www.scholarpedia.org/article/Path_integral). In that article equations (3), (18), and (19) include the normalization discussed above.
Hope this is more helpful
So, in case anyone is too lazy to read Feynman’s Nobel lecture, here’s the story:
So it’s a great story, and illuminating, but it doesn’t have much to say about the “constant of proportionality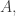 suitably adjusted.” That’s what I’m interested in now!
suitably adjusted.” That’s what I’m interested in now!
Professor Baez, I should probably try to clarify my comment about the constraints on the kind of number to represent “possibility.” (No greater-than, less-than relation, A+B= B+A. AB = BA. AB/B=A.) There are lots of other models for “possibility.” But here’s why I like Jon Barwise’s model from his paper “Information and Impossibilities.”
First here’s a link to a perhaps motivating quote. It’s what a student of Max Born, Herbert S. Green in Matrix Mechanics wrote about “possibility.”
(https://docs.google.com/file/d/0B9LMgeIAqlIEUnhiTHFyNWRTU2c/edit?usp=docslist_api)
The constraints are a way of trying to abstract from this a minimal structure.
Next from Barwise: “The Inverse Relationship Principle: Whenever there is an increase in available information there is a corresponding decrease in possibilities, and vice versa.”
Factoring away a possibility (AB/B=A) means fewer possibilities and for example in a slit experiment more information about where the particle will land. Multiplying (AB) meams increasing the possibilities and therefore less information about where the particle will land.
Green’s statement has for its semantic context the Heisenberg picture, where probability is constant and not a function of time, moreover in an experiment measured over a finite (not infinite or infinitesimal) situation. But when probability becomes a function of time then the time-varying probability could for example be a sine wave which over the finite situation averages to the very same constant probability. For each higher range of frequencies there could exist a theory with time-varying probability which averages to the same, constant probability of the finite situation. Does “possibility” also work like this?– for higher ranges of frequencies the theory for each range expresses time-varying possibilities which “average” to the same constant possibility as in the finite situation. If so, is there an equation using quantropy?
It is only a thought in a walk.


If the path integral have an analogy with the partition function, then there is a number of trajectories (that connect the space points with infinitesimal distance) for each four-dimensional volume.
I use the free particle propagator, so that seem that the “volume” of a single trajectory is
so the number of trajectories in a “volume” is:
it seem that the Schrodinger equation, or the equivalent path integral, say that the four-dimensional volume is quantized (like an electron in an atom) when the space is little (there is a minimum volume for a single trajectory), and that the movement is like an intersection of fluxes tube in the space; this don’t give new information, because it contain only old physics.
For a quantum particle moving in 1d space we need a quantity with dimensions of length to make the partition function dimensionless. In 3d space we’d need something with dimensions of length cubed (which we could get from something with dimensions of length). I don’t think we’d need something with dimensions of 4d volume.
with dimensions of length to make the partition function dimensionless. In 3d space we’d need something with dimensions of length cubed (which we could get from something with dimensions of length). I don’t think we’d need something with dimensions of 4d volume.
But anyway, your thoughts are interesting, though a bit mysterious.
Interesting stuff!
Instead of looking at it from the statistical thermodynamics point of view, you could look also at it from the phenomenological thermodynamic point of view. There, you have the relation
dS=dQ/T
I am always intrigued by this formula, it holds exactly, but you need to know nothing about quantum mechanics or statistical mechanics. In fact, it is much older I believe than the discovery of the atom.
Translating this to quantum mechanics (S is now action instead of entropy):
dQ=dS/(ih)
But in contrast to T in thermodynamics, ih is a constant. So:
Q = S/ih + constant.
Hmm.., is quantropy just a constant times action?
Gerard
westy31,
Or perhaps S/quantropy is uncertainty in the amount of action?
That one brings us back to the starting point of Heisenberg.
From a statistical mechanics point of view you can see the relation between quantropy and action in our paper:
Here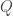 is the quantropy,
is the quantropy,  is the expected value of the action, and
is the expected value of the action, and  is the partition function.
is the partition function.  is the free action, the quantity analogous to free energy in the analogy we’re discussing.
is the free action, the quantity analogous to free energy in the analogy we’re discussing.
So, I think Gerhard’s clever argument that quantropy is proportional to (the expected value of the) action must be somewhat flawed. I’m not sure what the flaw is, but it could be than in the thermodynamics formula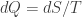 we are considering how
we are considering how 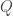 (which now means heat) and
(which now means heat) and  (entropy) vary as we change the temperature, which is analogous to
(entropy) vary as we change the temperature, which is analogous to  but later in the argument Gerhard is treating
but later in the argument Gerhard is treating 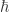 as fixed. I think we need to treat
as fixed. I think we need to treat 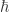 as variable to get the analogy to work. This may be upsetting to some, but it’s mathematically valid… and then it invalidates Gerhard’s step where he treats
as variable to get the analogy to work. This may be upsetting to some, but it’s mathematically valid… and then it invalidates Gerhard’s step where he treats 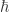 as constant. Maybe this is why he’s getting
as constant. Maybe this is why he’s getting
in my notation.
Just a guess.
I can think of a thermodynamical system that has a constant temperature (T), just like the quantum analogy, where ih is constant: An evaporating liquid with a very low specific heat, but with a considerable heat of evaporation (H). If n were the number of molecules in the vapour phase, the energy would be nH, and the entropy would be nH/T_boil.
This is a bit like a quantum system with a collection of spins, which can be UP or DOWN, with different energies. I do not know if the total expected action of such a system could be proportional to the number of particles in the UP state?
About the formula with the partition function (Z).
Could it be that ln(Z) is also a constant? In that case our formulas would agree. ln(Z) could be interpreted as the vacuum quantropy. With the thermodynamic system, you could also add a zero point entropy. This term would be arbitrary in phenomenological thermodynamics, but in statistical mechanics it would be something like the number of ways of rearranging the vacuum.
I do not have a good intuition of what it means to add action to a quantum system, but maybe this discussion is a good exercise for that!
Gerard
Gerard wrote:
No, it’s not. I suggest reading our paper—it’s easy and fun! In thermodynamics, is the free energy. In quantum mechanics,
is the free energy. In quantum mechanics,  is the ‘free action’.
is the ‘free action’.
Reply to John’s answer:
I did sort of read your article (spent a couple of hours on it).
It seems to me that Z is a sum over all microstates, weighted by exp(-E/kt) or exp(-S/ih) respectively. What puzzles me is whether this is ‘constant’. With constant I mean the same for a vacuum as for an excited field. I thought Z was a property of the system, regardless of its actual state, whereas depends on some kind way of adding action, for example by creating particles. This is really something I would like to understand.
depends on some kind way of adding action, for example by creating particles. This is really something I would like to understand.
Gerard
Gerard wrote:
In statistical mechanics Z is a sum over all microstates, weighted by
In quantum mechanics Z is a sum over all histories, weighted by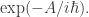 (I’m going to continue writing A for action and S for entropy, because otherwise things will get very confusing.)
(I’m going to continue writing A for action and S for entropy, because otherwise things will get very confusing.)
Microstates are ways a system can be at a given time. Histories are ways a system can be over all time, or a duration of time.
I’d say it’s constant—so constant that your last statement barely makes sense. Z is not defined ‘for a vacuum’ or ‘for an excited field’. Z is just a property of the system, depending only on (in statistical mechanics) or Planck’s constant
(in statistical mechanics) or Planck’s constant 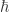 (in quantum mechanics).
(in quantum mechanics).
We can change the definition of so it depends on other things, like the volume of a box containing the system. This is very useful. But our paper doesn’t talk about that.
so it depends on other things, like the volume of a box containing the system. This is very useful. But our paper doesn’t talk about that.
Aha. Actually, I suggested in a previous post I suggested that it *was* constant. Perhaps we should make more clear: constant with respect to what.
I am trying to understand d(Quantropy) = d(Action)/ih.
This would imply Quantropy = (Action)/ih + Constant.
It would all make sense if the constant would be ln(Z).
‘constant’ in the thermodynamic case would mean it does not depend on temperature. You have for a constant temperature system:
d(Entropy) = d(Energy)/kT
-> Entropy = Energy/kT + Constant
I gave an example of a constant temperature system 2 posts ago, this formula would make sense for such a system.
The constant in this case is the entropy at zero temperature.
So in the quantum case, ln(Z) is ‘constant’ in the same sense, it does not depend on the amount of action added to the vacuum.
I assume that an excited system has a different action than the vacuum, and that you can go from the vacuum to the excited state by successive excitations.
That is how I interpret
d(Quantropy) = d(Action)/ih
Gerard
Isn’t dQ = T dS only valid for a reversible process in closed systems? I haven’t thought this through at all, but perhaps the ‘closed’ assumption doesn’t hold in the quantropy analogy.
Frederik wrote:
That sounds true. In a general quantum system, I think the only way I can change the analogues of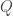 and
and  is by changing
is by changing 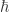 (which is analogous to
(which is analogous to 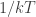 ). I can check to see whether the relation analogous to
). I can check to see whether the relation analogous to 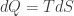 holds when I do this. The analogy to statistical mechanics is very good, so it should.
holds when I do this. The analogy to statistical mechanics is very good, so it should.
In a more specific quantum system I would adjust more parameters, just as in a more specific thermodynamic system, like a gas in a piston, I can change the volume as well as the temperature.
The name is “Munkhammar” (the “r” is missing everywhere)
Whoops! That’s embarrassing.
Fixed! Thanks.
Hi John,
I have been working some years in private on entropic priors, albeit from the Bayesian inference point of view. It’s one of my two favorite math subjects.
So I remembered that Saul Youssef wrote a couple of papers on getting quantum physics from “exotic” probabilities, and he has a page of references related to it (including his own papers):
http://physics.bu.edu/~youssef/quantum/quantum_refs.html
If I got it right then there is a difference to your approach: He does not use the maximum entropy principle, but directly applies the Cox axioms (frequently used to derive the ME principle) to real and complex numbers and even quaternions, and he claims that he gets statistical mechanics, quantum theory and Dirac theory from it, respectively.
By the way, have you not been tempted to work out the analogy with black hole thermodynamics? Its fun, you get meaningful things like area of the event horizon and so on…
Best wishes
Till
This Nobel prize winner has a fun piece on the future of physics:
• Frank Wilczek, Physics in 100 years.
The first part is about SO(1O) grand unification, etc.—good stuff to know, but not new. Then he says something that reminds me of my paper with Blake on quantropy, and my claim that all minimum principles may boil down to some sort of generalization of Occam’s razor (minimizing algorithmic complexity for hypotheses):
The relation of fundamental physics to information is certainly a tightly woven web. I also was interested by what Frank had to say in that article about Gravi-GUT unification:
“Although general relativity is based on broadly the same principle of local symmetry that guides us to the other interactions, its implementation of that principle is significantly different. The near-equality of unified coupling strengths, as we just discussed, powerfully suggests that there should be a unified theory including all four forces, but that fact in itself does not tell us how to achieve it.
String theory may offer a framework in which such four-force unification can be achieved. This is not the event, and I am not the person, to review the vast amount of work that has been done in that direction, so far with inconclusive results. It would be disappointing if string theory does not, in future years, make more direct contact with empirical reality. There are many possibilities, including some hint of additional spatial dimensions (i.e., a useful larger broken symmetry SO(1, N) → SO(1, 3))…”
If he continues that line, he’ll see that he needs to use at least spin(11,3) to include gravity and the gauge fields acting on a fermion generation, or spin(12,4) if he wishes to have de Sitter spacetime, at which point he’ll be looking at e8(-24). I’ll have to ask him about that at some point. I do hope Frank will reconsider his strong favorable stance on supersymmetry once he has to pay up on a bet on it in a few months.
I would quite like to see some of these quantropy calculations in the context of the harmonic oscillator. I feel I have some chance of understanding a calculation done in a countable dimensional vector space.
Or is this left as an exercise for the reader?
All the Hilbert spaces used in physics are countable dimensional. But anyway, I agree that after the free particle, the harmonic oscillator is the next example to study!
My student Blake Pollard was once planning to write a paper on the quantropy of the harmonic oscillator. He did a bunch of calculations, but he got distracted by other things (like trying to write a thesis). I doubt he’ll come back to that project. So, anyone who wants should give it a try and report back.
Back then I did some calculations on the harmonic oscillator. If I remember correctly they ran out of hand pretty quickly and got filed away with the comment “hard work or idea needed”.
I would also like to see some progression here.
Roger Balian tried to mix equilibrium statistical mechanics with quantum states in his work “Justification of the Maximum Entropy Criterion in Quantum Mechanics”. https://link.springer.com/chapter/10.1007/978-94-015-7860-8_9
Dears Mr. Baez and Mr. Pollard,
I’ve read your article and found it profoundly interesting. I would be honored if you answered me a couple of questions that came to my mind while studying it.
There is one point I don’t really get: why do you choose to speak of histories instead of paths and then feel allowed to use standard Lebesgue integrals instead of path integrals?
I tried to reformulate the article by using path integrals and I have noticed no serious additional complication.
Moreover, I had the feeling that some important property of quantropy was missing in order to establish a real analogy with entropy: the additivity. I’ve made a proof myself and would be glad to show you.
Thank you for the attention,
Fulvio Bergadano