guest post by Alastair Jamieson-Lane
The world is complex, and making choices in a complex world is sometimes difficult.
As any leader knows, decisions must often be made with incomplete information. To make matters worse, the experts and scientists who are meant to advise on these important matters are also doing so with incomplete information—usually limited to only one or two specialist fields. When decisions need to be made that are dependent on multiple real-world systems, and your various advisors find it difficult to communicate, this can be problematic!
The generally accepted approach is to listen to whichever advisor tells you the things you want to hear.
When such an approach fails (for whatever mysterious and inexplicable reason) it might be prudent to consider such approaches as Bayesian inference, analysis of competing hypotheses or cross-impact balance analysis.
Because these methods require experts to formalize their opinions in an explicit, discipline neutral manner, we avoid many of the problems mentioned above. Also, if everything goes horribly wrong, you can blame the algorithm, and send the rioting public down to the local university to complain there.
In this blog article I will describe cross-impact balance analysis and a recent extension to this method, explaining its use, as well as some basic mathematical underpinnings. No familiarity with cross-impact balance analysis will be required.
Wait—who is this guy?
Since this is my first time writing a blog post here, I hear introductions are in order.
Hi. I’m Alastair.
I am currently a Master’s student at the University of British Columbia, studying mathematics. In particular, I’m aiming to use evolutionary game theory to study academic publishing and hiring practices… and from there hopefully move on to studying governments (we’ll see how the PhD goes). I figure that both those systems seem important to solving the problems we’ve built for ourselves, and both may be under increasing pressure in coming years.
But that’s not what I’m here for today! Today I’m here to tell the story of cross-impact balance analysis, a tool I was introduced to at the complex systems summer school in Santa Fe.
The story
Suppose (for example) that the local oracle has foretold that burning the forests will anger the nature gods…
… and that if you do not put restrictions in place, your crops will wither and die.
Well, that doesn’t sound very good.
The merchant’s guild claims that such restrictions will cause all trade to grind to a halt.
Your most trusted generals point out that weakened trade will leave you vulnerable to invasion from all neighboring kingdoms.
The sailors guild adds that the wrath of Poseidon might make nautical trade more difficult.
The alchemists propose alternative sources of heat…
… while the druids propose special crops as a way of resisting the wrath of the gods…
… and so on.
Given this complex web of interaction, it might be a good time to consult the philosophers.
Overview of CIB
This brings us to the question of what CIB (Cross-Impact Balance) analysis is, and how to use it.
At its heart, CIB analysis demands this: first, you must consider what aspects of the world you are interested in studying. This could be environmental or economic status, military expenditure, or the laws governing genetic modification. These we refer to as “descriptors”. For each “descriptor” we must create a list of possible “states”.
For example, if the descriptor we are interested in were “global temperature change” our states might be “+5 degree”, “+4 degrees” and so on down to “-2 degrees”.
The states of a descriptor are not meant to be all-encompassing, or offer complete detail, and they need not be numerical. For example, the descriptor “Agricultural policy” might have such states as “Permaculture subsidy”, “Genetic engineering”, “Intensive farming” or “No policy”.
For each of these states, we ask our panel of experts whether such a state would increase or decrease the tendency for some other descriptor to be in a particular state.
For example, we might ask: “On a scale from -3 to 3, how much does the agricultural policy of Intensive farming increase the probability that we will see global temperature increases of +2 degrees?”
By combining the opinions of a variety of experts in each field, and weighting based on certainty and expertise, we are able to construct matrices, much like the one below:

The above matrix is a description of my ant farm. The health of my colony is determined by the population, income, and education levels of my ants. For a less ant focused version of the above, please refer to:
• Elisabeth A. Lloyd and Vanessa J. Schweizer, Objectivity and a comparison of methodological scenario approaches for climate change research, Synthese (2013).
For any possible combination of descriptor states (referred to as a scenario) we can calculate the total impact on all possible descriptors. In the current scenario we have low population, high income and medium education (see highlighted rows).
Because the current scenario has high ant income, this strongly influences us to have low population (+3) and prevents a jump to high population (-3). This combined with the non-influence from education (zeros) leads to low population being the most favoured state for our population descriptor. Thus we expect no change. We say this is “consistent”.
Education however sees a different story. Here we have a strong influence towards high education levels (summing the column gives a total of 13). Thus our current state (medium education) is inconsistent, and we would expect the abundance of ant wealth to lead to an improvements in the ant schooling system.
Classical CIB analysis acts as a way to classify which hypothetical situations are consistent, and which are not.
Now, it is all well and good to claim that some scenarios are stable, but the real use of such a tool is in predicting (and influencing) the future.
By applying a deterministic rule that determines how inconsistencies are resolved, we can produce a “succession rule”. The most straight-forward example is to replace all descriptor states with whichever state is most favoured by the current scenario. In the example above we would switch to “Low population, medium income, high education”. A generation later we would switch back to “Low population, High income, medium education”, soon finding ourselves trapped in a loop.
All such rules will always lead to either a loop or a “sink”: a self consistent scenario which is succeeded only by itself.
So, how can we use this? How will this help us deal with the wrath of the gods (or ant farms)?
Firstly: we can identify loops and consistent scenarios which we believe are most favourable. It’s all well and good imagining some future utopia, but if it is inconsistent with itself, and will immediately lead to a slide into less favourable scenarios then we should not aim for it, we should find that most favourable realistic scenario and aim for that one.
Secondly: We can examine all our consistent scenarios, and determine whose “basin of attraction” we find ourselves in: that is, which scenario are we likely to end up in.
Thirdly: Suppose we could change our influence matrix slightly? How would we change it to favour scenarios we most prefer? If you don’t like the rules, change the game—or at the very least find out WHAT we would need to change to have the best effect.
Concerns and caveats
So… what are the problems we might encounter? What are the drawbacks?
Well, first of all, we note that the real world does not tend to reach any form of eternal static scenario or perfect cycle. The fact that our model does might be regarded as reason for suspicion.
Secondly, although the classical method contains succession analysis, this analysis is not necessarily intended as a completely literal “prediction” of events. It gives a rough idea of the basins of attraction of our cycles and consistent scenarios, but is also somewhat arbitrary. What succession rule is most appropriate? Do all descriptors update simultaneously? Or only the one with the most “pressure”? Are our descriptors given in order of malleability, and only the fastest changing descriptor will change?
Thirdly, in collapsing our description of the world down into a finite number of states we are ignoring many tiny details. Most of these details are not important, but in assuming that our succession rules are deterministic, we imply that these details have no impact whatsoever.
If we instead treat succession as a somewhat random process, the first two of these problems can be solved, and the third somewhat reduced.
Stochastic succession
In the classical CIB succession analysis, some rule is selected which deterministically decides which scenario follows from the present. Stochastic succession analysis instead tells us the probability that a given scenario will lead to another.
The simplest example of a stochastic succession rule is to simply select a single descriptor at random each time step, and only consider updates that might happen to that descriptor. This we refer to as dice succession. This (in some ways) represents hidden information: two systems that might look identical on the surface from the point of view of our very blockish CIB analysis might be different enough underneath to lead to different outcomes. If we have a shaky agricultural system, but a large amount of up-and-coming research, then which of these two factors becomes important first is down to the luck of the draw. Rather than attempt to model this fine detail, we instead merely accept it and incorporate this uncertainty into our model.
Even this most simplistic change leads to dramatics effects on our system. Most importantly, almost all cycles vanish from our results, as forks in the road allow us to diverge from the path of the cycle.

We can take stochastic succession further and consider more exotic rules for our transitions, ones that allow any transition to take place, not merely those that are most favored. For example:
Here is our current scenario,
is some possible future scenario, and
is the total impact score of
from the perspective of
.
is a simple normalizing constant, and
is our system’s temperature. High temperature systems are dominated by random noise, while low temperature systems are dominated by the influences described by our experts.
Impact score is calculated by summing the impact of each state of our current scenario, on each state of our target scenario. For example, for the above, suppose we want to find when
is the given scenario “Low population, High income, medium education” and
was the scenario “Medium population, medium income, High education”. We consider all numbers that are in rows which were states of
and in columns that are states of
. This would give:
Here each bracket refers to the sum of a particular column.
More generically we can write the formula as:
Here refers to an entry in our cross-impact balance matrix,
and
are both states, and
reads as “
is a state of
”.
We refer to this function for computing transition probabilities as the Boltzmann succession law, due to its similarity to the Boltzmann distribution found in physics. We use it merely as an example, and by no means wish to imply that we expect the transitions for our true system to act in a precisely Boltzmann-like manner. Alternative functions can, and should, be experimented with. The Boltzmann succession law is however an effective example and has a number of nice properties: is always positive, unchanged by adding a constant to every element of the cross-impact balance matrix, contains adjustable parameters, and unbounded above.
The Boltzmann succession rule is what I will refer to as fully stochastic: it allows transitions even against our experts’ judgement (with low probability). This is in contrast to dice succession which picks a direction at random, but still contains scenarios from which our system can not escape.
Effects of stochastic succession
‘Partially stochastic’ processes such as the dice rule have very limited effect on the long term behavior of the model. Aside from removing most cycles, they behave almost exactly like our deterministic succession rules. So, let us instead discuss the more interesting fully stochastic succession rules.
In the fully stochastic system we can ask “after a very long time, what is the probability we will be in scenario ?”
By asking this question we can get some idea of the relative importance of all our future scenarios and states.
For example, if the scenario “high population, low education, low income” has a 40% probability in the long term, while most other scenarios have a probability of 0.2%, we can see that this scenario is crucial to the understanding of our system. Often scenarios already identified by deterministic succession analysis are the ones with the greatest long term probability—but by looking at long term probability we also gain information about the relative importance of each scenario.
In addition, we can encounter scenarios which are themselves inconsistent, but form cycles and/or clusters of interconnected scenarios. We can also notice scenarios that while technically ‘consistent’ in the deterministic rules are only barely so, and have limited weight due to a limited basin of attraction. We might identify scenarios that seem familiar in the real world, but are apparently highly unlikely in our analysis, indicating either that we should expect change… or perhaps suggesting a missing descriptor or a cross-impact in need of tweaking.
Armed with such a model, we can investigate what we can do to increase the short term and long term likelihood of desirable scenarios, and decrease the likelihood of undesirable scenarios.
Some further reading
As a last note, here are a few freely available resources that may prove useful. For a more formal introduction to CIB, try:
• Wolfgang Weimer-Jehle, Cross-impact balances: a system-theoretical approach to cross-impact analysis, Technological Forecasting & Social Change 73 (2006), 334–361.
• Wolfgang Weimer-Jehle, Properties of cross-impact balance analysis.
You can find free software for doing a classical CIB analysis here:
• ZIRIUS, ScenarioWizard.
ZIRIUS is the Research Center for Interdisciplinary Risk and Innovation Studies of the University of Stuttgart.
Here are some examples of CIB in action:
• Gerhard Fuchs, Ulrich Fahl, Andreas Pyka, Udo Staber, Stefan Voegele and Wolfgang Weimer-Jehle, Generating innovation scenarios using the cross-impact methodology, Department of Economics, University of Bremen, Discussion-Papers Series No. 007-2008.
• Ortwin Renn, Alexander Jager, Jurgen Deuschle and Wolfgang Weimer-Jehle, A normative-functional concept of sustainability and its indicators, International Journal of Global Environmental Issues, 9 (2008), 291–317.
Finally, this page contains a more complete list of articles, both practical and theoretical:
• ZIRIUS, Cross-impact balance analysis: publications.







Brilliant!
Very nice post. It looks a lot (especially the first part) like you have a discrete-time dynamical system and are trying to see which states are actually equilibria and what is their region of attraction.
The dynamic system looks linear though, if so then perhaps this might be a limitation for more complex models …
Anyway, very interesting, thanks!
Actually now i see i was wrong, the system is nonlinear. Actually i’d say it has just the right amount of nonlinearity to usefully describe a lot of behaviors. This is very cool!
It is interesting.
I am thinking that the ant farm analogy can be more than an analogy.
If there are many different ant colonies, with many different queens, then each colony have a similar genetic behavior; then the multiple objective of the colonies give a better fit with the environment, that is a number of descriptors (that can have different states that the colony measure).
The stochastic succession can be the description of the genetic change of the queens that give different behavior of the colonies in the environment, so that I think that each environment have the optimal ant colony for stochastic-genetic evolution.
Reminds me of what Pascal had to say about the confirmation bias of political leaders, …kind of. (Pensées #100 on Self Love. It’s about a page long and easy to find online.) Strangely modern in its psychological insight, considering he was writing in c1640. For me, Pascal’s short text explains what it is about the structure of society and human nature that ensures leaders are surrounded by confirmers of their bias, and explains why leaders become ‘bunker-bound’ and increasingly ‘out of touch’, the longer they are in power.
Great post by the way. Really enjoyed it. I’m not 100% sure that starting with input from “our panel of experts” is not already problematic though. (Whose panel? Which experts? Who decides which fields are relevant and which are not?) I’m not sure we escape from the jaws of confirmation bias that way. At least, not with a single bound.
I’m not a mathematician and I may well be missing the point here, but anyway…
My own interest is more in the structures of collective decision making, which you mention in passing here, but which I see from elsewhere that you have a stong interest in. That seems to be an area where rationality is particularly conspicuous by its absence, …or rather, by it’s level of convolution. I can’t see that the global cooperation needed to avert disasterous anthropogenic climate change can be achieved without radically changing the existing collective decision-making structures. As I see it, those structures evolved against a backdrop of tribal/national competition where the natural environment’s capacity for benign absorption of waste products was so close to being infinite that it made no difference, and was (quite properly) ignored in the (implicit) models that underlie those structures.
However, If there is no longer any place corresponding to the term ‘away’ into which to ‘throw’ waste, and no longer any people who are so ‘other’ as to have no impact on one’s world as long as one can keep them outside one’s borders, then the (implicit) model breaks down. It may have reached its own ‘boundary conditions’, so to say. The question is whether the model is so deeply engrained that it will survive global catastrophe and survive its human host’s destruction. It may even perhaps re-create the external conditions in which it again makes sense. (E.g. a post-apocalyptic world with population at below 5% of current levels with low education levels and limited technology? A world where ‘away’ is a virtually infinite place again.)
Paul wrote:
Of course it’s problematic: everything about guessing the future is problematic. When advertising this post over on G+, I wrote:
So the point is not to do things in an unproblematic way, but just try a new way to do things that may avoid some of the problems other ways have.
Yes, I agree John. All prediction is problematic, especially when trying to predict the future! Thanks for highlighting that. My comment was not meant as a criticism, although I can see how it might have seemed that way.. Alistair’s mention of (or link to) confirmation bias jumped out at me and got me thinking about which ideas do or do not come to influence public policy. It seems to me that public policy is very rarely driven by science or rationality; it seems to be predominantly driven by something else, and I am intrigued to know what that ‘something else’ could be.
When I asked you last week whether you thought our lack of success so far in tackling climate change was because we don’t understand networks well enough, I wasn’t being rhetorical: my feeling is, that that IS the case, and that in the context of climate change, some of the most important networks to understand are the ones that underlie human, social and especially political behaviour.
(BTW, I’m sorry to have missed your second talk on Tuesday – I couldn’t get away from work in time. Did anyone video it?)
Paul wrote:
Okay, thanks for clarifying! I agree that human social, economic and political behavior is the main uncontrolled and poorly-understood variable when it comes to dealing with global warming. I’m less sure that we can understand it quickly enough, and even less sure that this understanding will help us quickly enough to solve the problem. Network theory could be very relevant here… but it’s possible that some other discovery could save the day.
Yes, Brendan plans to videotape all the talks, and the one you’re talking about is here:
• Tuesday 25 February, 3:30 pm: Network Theory I: electrical circuits and signal-flow graphs. See the slides or watch a video.
There is a simpler and more accurate way to understand global inability to tackle climate change, and this leads directly to a strategy.
Fossil fuel deposits such as oil and gas fields, coal mines, etc., become assets on their owners’ balance sheets as soon as they have been discovered and the estimates of their capacity have passed industry peer review.
For example if you are an oil company and your test drilling in a given area indicates a probable extractable quantity Q of oil, there is a formula for calculating the asset value of that oil to your company. That asset is added to your balance sheet, and to the financial value of your company as reflected in shares of stock and share price.
However, any and all proposed policies to address climate change will necessarily impact your estimates of the extraction schedule of your oil from that newly-discovered oil field, and the value of the oil when extracted. There is exactly no way to address climate change without impacting the asset value of unproduced fossil fuel resources. (Actually there is one: which is for some combination of governments and private sector entities to buy out the necessary assets, but the price of doing so would be absolutely prohibitive at anticipated asset prices. Aside from that, all other methods impact the asset value.)
This is equivalent to someone buying a piece of real estate, and then expecting to develop it under existing building codes, but then having to face a possible change in the codes that will impact your ability to develop the property as you expected (for example an upgraded requirement for seismic strength of buildings). The bottom line is, the owner of the real estate (or the oil field, the coal mine, etc.) will view this as policy makers attempting to radically devalue their assets, or to put it bluntly, steal their money.
So: How would you react if you were sitting on a pile of money and someone planned to take a substantial chunk of it, possibly most of it? You’d fight tooth and nail to stop them. For example you might spend X percent of the value of that money to hire armed guards to protect it.
That is exactly what is happening in the climate arena. Fossil fuel companies are hiring PR firms, lobbyists, lawyers, and (directly or indirectly) buying off scientists, government officials, etc., to protect their assets, even at the potential future cost of a climate catastrophe.
Ultimately this comes down to a fight at the level of pure power politics and attack vs. defense. Owners of fossil fuel assets use political, legal, and economic power to defend their unproduced asset value. We, climate activists, must use the same types of power to attack the fossil fuel companies’ unproduced asset value.
Those are the defining terms of the war, and the only relevant questions from that point forward are about how to wage that war successfully. For example, what combination of legislation, economic pressure, lawsuits, executive action, etc., is necessary to overpower the fossil fuel asset owners? Can they be overpowered by indirect means i.e. “stealth tactics” of one kind or another? What are their weaknesses, and how can those weaknesses be exploited?
You can be quite sure that the fossil fuel companies and their allies are engaged in that kind of analysis. One of their tactics is to tie us up wasting our time fighting on false battle fronts, such as the various “culture war” aspects of this. The time and effort we spend trying to “explain” ourselves and “defend” climate science against denialists, are complete waste. We have to stop playing defense and start playing offense: go on the attack, at the critical targets.
I agree with this analysis in large part. Alas, I don’t know how to personally be effective in “going on the attack at the critical targets”.
Regardless of this issue, I think scenarios modelling using cross-impact balance analysis can be useful for many things. It could even be useful for answering questions like these:
However, as a technology, cross-impact balance analysis can be used for ill as well as for good.
To add to John’s comment, a number of papers discuss these very issues of whose judgments are behind a CIB analysis (or even a traditional scenario analysis). Ideally, CIB analyses will make a point to investigate judgment diversity. Sometimes differences in judgments that one might hypothesize should matter do not, and vice versa.
See Lloyd and Schweizer (2013), Schweizer and Kriegler (2012), and Kemp-Benedict (2012).
Maybe you could pick up the financial engineering and accounting lingo, infiltrate a ratings company like Fitch or Moody’s, and introduce a new way to rate a company for financial investment based on its impact on climate change. Some years ago Robert Kaplan at Harvard tried to introduce “activity based accounting” and there may be some lessons learned from that. Also from ancient times and of possible relevance, here’s a letter I wrote to the Financial Accounting Standards Board (FASB) on request from the leaders of a project on intangible assets at the Brookings Institution.
I should add that because it includes the building, workpoint costing as in the above link is probably a logical place to account for the costs of addressing climate change.
Click to access The%20Accounting%20Classification.pdf
Alternatively, you could just play SimCity.
Or, a SimCity tournament, for example a tournament held at the end of classes in game theory for climate change in behavioral economics at SimSchool, where Certified Fraud Examiners take classes to become CCCEs (Certified Climate Change Examiners– motto: “Where there’s smoke there’s fire.”)
Paul wrote:
“(Whose panel? Which experts? Who decides which fields are relevant and which are not?)”
Perhaps those trained in negotiation games as part of becoming a CCCE.
There is a way to run the ultimatum game in order to learn how either spite (from injustice) or gratitude (from a gift) can determine the outcome of the negotiation. Here’s a poster from a meeting of the Society for the Quantitative Analysis of Behavior. It could be a negotiation over how to draw a network either in the tournament, or in the behavioral economics lab.
https://docs.google.com/file/d/0B9LMgeIAqlIEZDIwb3lEdnpueVk/edit?usp=docslist_api
Honestly…This was actually one of my concerns coming at the above model. I’m a mathematician, so the idea of a model that isn’t PERFECTLY accurate kind of concerns me. My collaborators (in Particular Vanessa, who will be publishing her own take on all of this in the next few weeks) explained that having some system is better than having none.
Personally… I’m still concerned. I’ld like to see the above scheme tested- perhaps finding a more short term issue, and getting clusters of “experts” to comment individually, via the above method (indirectly) and after some real world discussion.
Do this a couple dozen times, and then see how the model fares after a year or so?
Hmmm… I don’t know. I’m no experimentalist, but I suspect that experiments should be done to determine if this thinking tool actually improves peoples ability to predict the future.
I used to be a pure mathematician, but I am an applied one now. These days I follow George Box’s maxim ‘All models are wrong, but some are useful’. Usefulness can be quantified via a utility function once you have some experimental results. The catch is, we don’t know how to combine different people’s utility functions.
Years ago when I got the money from my former company to pay researchers at USC to do the above experiment, the literature said that teams solving problems usually perform less competently than their highest performing individual. Which means that the best strategy would be to have the highest performer solve the problem while everybody else goes on coffee break. Which of course, will never happen in the real world. However–
There is one exception to this: groups of two or “dyads.” Compared to any other size team, only dyads have the capability to outperform the team’s most competent individual.
I had always seen this as experimental confirmation of a theoretical and purely mathematical prediction in Theory of Games– that only teams of two can reach “perfect competition.”
There were many next steps that we had in mind, including tournaments of dyads at the end of math classes, scoring each dyad on daily quizzes, then the next day randomly re-assigning members to a different partner– with high probability to be matched with a different partner who scored roughly the same as your previous dyad, and low probability to be matched with a different partner who scored radically different from your previous dyad. Would the tournament work like the genetic algorithm and continuously increase scores? Nobody knows. Many people, including myself, left the company. That’s simply how it goes in industrial research.
Here’s a representative paper on dyadic problem solving–
Click to access dyad_abstraction.pdf
The map and the territory.
Maps are always simplifications of the territory. If they weren’t simplifications they wouldn’t be maps. If they weren’t simpler than the territory they would be of little use.
I think we can say the same for models. A model is essentially a map.
Systems in the real world are complicated and messy. That’s why we need maps and models. It’s not possible to model a system in a 100% accurate way unless the system you are modelling is itself a model (or an idealised conception of a real-world situation.)
The degree to which a model is usefully accurate is best determined by running many, many iterations and comparing output against the real world. But modelling something like climate change or population change does not afford one the opportunity to run many iterations, so the feedback we get from reality is limited.
Also, when models which are intended to model complex systems as closely as possible get so complicated that they are no longer accessible to human intuition, then yes, they potentially are very useful, but there is also a danger of mistaking their precision for accuracy. Errors can lurk for a long time undiscovered in very complex models.
The value I see in models is not so much that they can output results that are necessarily 100% accurate, but more that they can create shifts in the ways that humans see things. Human behaviour, including political, economic and social behaviour, is driven by the way that those humans see things, and it is driven by nothing else.
Ha ha- this map and territory business sounds very similar to a lot of stuff I’ve been reading recently (Eleizer Yudkowsky). I wonder if that is the source, or if that description of the world is older than my current understanding… Anyway
Yes- the model is necessarily a simplification, but I guess there are some simplifications that seem justifiable, and others that don’t… and I guess sometimes it depends on our understanding of the underlying system:
I “understand” particles, thus simplifying to thermodynamics seems acceptable. I don’t “understand” political decision making, therefore I don’t know how best to simplify… although of course even the particles themselves are simplifications of deeper systems which I don’t understand- exist in the map, but possibly not the territory.
But yes- My point is not that I expect models to be 100% accurate, but that this type of model seems hard to test before it is used. Until tests are done we don’t KNOW the models accuracy- having a map but no way to compare it to the territory is a BAD IDEA.
So… tests probably need to be done somehow (Like I said earlier, small, faster systems seem a good candidate)- it doesn’t mean it WILL work for larger slower systems, but would definitely give me some more faith in the method.
It’s nice to see some examples of the probability distributions that show up in examples of the Boltzmann succession rule:
This is a simple example, just to illustrate the ideas. The idea is that we’ve got a developing country where the population, income and education can be high, medium or low. For example, the big red dot HLL has high population, low income, and low education. That’s a very self-consistent scenario. Other scenarios like HML and LLL are less self-consistent: if we start there, the situation will tend to move towards HLL.
This example is from:
• Vanessa Schweizer, Alastair Jamieson-Lane, Nix Barnett, Hua Cai, Stephan Lehner, Matteo Smerlak, Melinda Varga, Complexity (trans‐)science: a project on forecasting social change.
which, alas, seems to be unavailable on the web.
Really interesting map.
This is my first post to Azimuth. It’s a companion to the one by Alaistair Jamieson-Lane. I’m an assistant professor at the University of Waterloo in Canada with the Centre for Knowledge […]
[…] “Markov Models of Social Change (Part 1)” https://johncarlosbaez.wordpress.com/2014/ … […]
test
sorry for the “test comment” above but I just wanted to know, wether my comments are “getting through” this time (they didn’t last time).
@Alistair:
Two questions: What do you do if you have an even number of states and the sum over the columns in one triple are equal?
The matrix above has the suggestive form that the numbers in each triple of the row add up to 0 apart from one (education low, income) so I assume this one exception is a typo and thus there is a constraint on the experts judgement which hasn’t been stated explicitly (or may be I overread this) but which is implicitly assumed to hold.
Is that right?
I ask because if you add a sufficiently large offset to each matrix entry so that each entry is larger equal 0 (like in the above this would be 11) then first this changes the sum (the total impact score) also only by a constant offset (in the matrix above that constant would be 11*3) and thus affects in particular not the order of each number in each triple and thus the choice of the new states (the “distinction” though changes, but this seems only to influence speed of convergence) and secondly apart from a factor, one has then blockwise a right stochastic matrix (that is in the above matrix the triples in a row sum to 33 and dividing each entry by 33 each row in a triple satisifies the condition of a right stochastic matrix, which is to sum to 1) . I think this gives a more “mathematical look” to what’s happening in classical CIB analysis.
On the other hand given all this one is tempted to ask why not take a blockwise right stochastic matrix from onset on and likewise use probabilities for classical CIB analysis. In particular if you apply your above procedure then this procedure is just multiplication with the matrix and THEN a sort of strange “projection onto the biggest”, where you sort of loose information. That is in particular if you iterate you would rather first multiply everthing and then project (…if at all).
Yes- the low education one is a typo (meant to be -4. Oh well).
In this particular example that has been an implicit assumption with respect to expert opinions. However, I don’t believe there is anything in the system that requires this (its just a nice way of reducing the number of free variables)
The example you give is nice, but has slight issues- for example what if I added 1000 instead (then divide by 3000). This would give a similarly stochastic matrix, but in one examples you have significant distinctions between levels (including several 0s), and in the other everything if very close to one.
Secondly, one of the more important parts of the CIB framework is combining influences by adding down a column.
Just because we are row stochastic, doesn’t mean our columns will add up in a nice way- in the above example, the influence towards “high education” would give 46/33- which clearly can’t be used as a probability.
At least… that’s my understanding of what you have described. Perhaps I have misunderstood.
No I think you have basically understood correctly.
yes, thats what I meant with “the distinction though changes”, that is if you add giantly large numbers then it will get hard to distinguish, but that would only be necessary if you have a very large negative number.
It’s a probability “up to a factor” that is if you want probabilities then the column sum has also to be normalized, that is you have to divide your total impact score by the number of rows you add together, then your row triples should add up to one again. If you would use weights, i.e. if you would multiply each row by a (nontrivial) factor then you would accordingly need to divide by the sum of the factors (or if the weight differs from triple to triple, accordingly by the sum of factors of each triple).
Yes but it comes from a certain way of judging. That is intrinsically those impact numbers, as you described them describe how “a state would increase or decrease the tendency for some other descriptor to be in a particular state” i.e. you want to describe, which state gets more or less likely, given a certain descriptor state and the probability description reflects this a very direct way.
If e.g. you just add any positive numbers, than this could mean that the impact numbers indicate how strong something grows, but that’s a totally different meaning than your description with the constraint and the judging would be different.
It should also be mentioned that readers usually think that if they see such a very nongeneric matrix that it was created as such on purpose.
Re: the comment from G above, to the effect that catastrophic climate change skepticism simply stems from people “sitting on a pile of money” that others want to take away — the analogies, and the logic, used to support this all assume that the people with the money are indifferent to the losses they would incur in the event of catastrophe (or are too stupid to see such losses), either of which seems unrealistic.
What if we look instead at the notion of actual value differences, which G seems to dismiss as “culture war aspects”. Consider the possibility of someone actually engaged in that culture war, but to a degree that they’re largely unconscious of. They too would tend to look upon the very idea of a “culture war”, aka a conflict of values, as a mere distraction, since they’ve externalized their values onto the world, and are unable to imagine the possibility of alternative values except as error or venality. Wouldn’t such a person sound a lot like G him/herself?
Metamorph, Here’s what strikes me about G’s comment: (a) the assets of a just-discovered but not yet pumped field are by accounting standards allowed to be entered onto the balance sheet, and (b) all liabilities from the asset (like polluted water supply about which which Parachute Colorado is suing) are implicitly passed to the people. But these assets are really intangible until they are actually pumped. The accounting standards allowing their entry onto the balance sheet are simply the conventions of business organizations participating in the accounting boards. Now let’s say that business organizations won’t do anything about climate change until it hits their pocketbooks. Well, we can see that the conventions of the club are now that liabilities are ignored, and intangible assets can be entered into the balance sheet. But is there a different way of accounting for costs that will make all of the costs of climate change visible to organizations, who are now in ignorance of the liabilities of climate change because it’s not on their balance sheets? Of course we can’t expect them to willingly adopt such an accounting system. So maybe it’s a balance sheet we assign to the people of, say, a city, county, state or nation (TBD). And let’s also say that it’s an costing system with theorem-proving assistance, like Homotopy Type Theory. The idea is that, although business organizations would still be ignorant of the costs of climate change because it doesn’t appear on their balance sheets, that the people would know about these costs because they are entered into this new kind of balance sheet, with climate change liabilities associated to deliverers. The new kind of balance sheet would be public information in anticipation of voting season. Clearly some mathematical research would be needed to iron all this out. In the mean time, I propose we call the desired accounting system “homotopic workpoint costing.” The details would have to be ironed out in a few workshops, say with network theory mathematicians, HoTT experts on proof assistants, perspective on fraud prevention, climate scientists, etc. To develop a market share for it, the Lanchester strategy would probably be best.
Thanks, Lee. My thoughts:
a) Real costs, including real (in the sense of broad agreement across varying value/belief systems) potential costs, of climate change and other externalities can and do appear on the balance sheets of different market actors — e.g., insurance companies, tourist services, etc. — and these costs can and do create legal liabilities for those that can be shown to be responsible for such costs. In this way, corporations and their investors are going to be generally aware of such liabilities, however they appear or fail to appear on their balance sheets — those that are not are subject to Darwinian-style pruning.
b) Deeper problems arise, however, when we’re dealing with issues that involve value/belief systems, or the sorts of issues that G simply dismissed as a “culture war”. These kinds of issues involve large abstractions like freedom and equality, the individual and the community, material vs. spiritual, etc. In these kinds of cases, the assessment of costs and trade-offs is inherently questionable, and all the more so the more global the scope of the issue and the longer the time-frames involved — on both of which factors, climate change is at an extreme end. In other words, I think that cultural/political conflict (aka “culture war”, though I think that term melodramatic) is embedded in the climate change issue, and this makes the calculation of real costs involved also problematic because of its inherently political implications.
c) I think there is sometimes a tendency toward what I would call technical utopianism, which believes it is possible either to resolve even disputes involving value/belief systems through some sort of mathematical formalism, or, better still, to bypass such disputes altogether in that way. The problem, as I see it, is that all such attempts are themselves embedded in human culture, and as such are infected by such value/belief systems prior to their application — i.e., they simply push up the value/belief disputes to a level above the formalism. (The science-fictional Hari Seldon, for example, and his band of Psychohistorians would themselves be carriers of value/belief systems, whether they are conscious of it or not — would have been an interesting plot device to consider a splinter group employing the same formalism but with a different value/belief system to block the rise of a new galactic empire.)
I concur with Metamorf that the technical utopians could be more helpful by directing their efforts to developing tools that help humans confront differences in value/belief systems. I am not saying that technical utopianism will get everyone to agree; what would be great is to develop technical tools that illuminate which differences matter for particular outcomes. Just as there can be value in knowing what you don’t know, it may be worthwhile to zero in on the particular disagreements that matter for a strategy. Then debates can develop in a more productive direction.
For instance, I would argue that a deist and an atheist do not have to agree on the existence of God in order to be equally concerned about climate change. Similarly, I doubt a capitalist and a communist have to agree on the relationship between the government and markets to find common ground on strategies for addressing climate change. However, the latter claim is often made, which distracts a lot of people and wastes everyone’s time (and some, like Naomi Oreskes, would charge that such tactics amount to ‘fiddling while Rome burns’).
I would certainly agree with Vanessa that anything that could illuminate which differences matter would be helpful. I’m just not sure that technical tools will do the trick when it comes to differences over value/belief systems.
For example: you don’t need to be a communist to believe that capitalism is wasteful, greed-ridden, and/or environmentally ruinous — and if you believe that, then you’re more likely to believe claims that some threat requires that we must control, reign in, or reduce capitalist exploitation now or the result will be catastrophic (“Rome is burning”, i.e.). Thus, you’ll tend to believe that opposition to such claims is simply driven by capitalist greed or shortsightedness (“Big Oil” i.e.), and you’ll want to favor strategies that directly impact such exploitation and waste, such as taxing or otherwise reducing fossil fuels, and disfavor or ignore strategies that don’t have such impact, such as adaptation, carbon capture, or active climate control.
On the other hand, if your value/belief system views capitalism as such as benign or a system that generates great good, then you’ll tend to be more skeptical of claims that we must control, reign in, or reduce its effects because of some threat. In fact, you’ll tend to be more skeptical of the threat itself, or of its immediacy, and in any case will be more open to strategies that don’t appear directly aimed at the capitalist economy.
In reality, of course, most people exhibit a mixture of such beliefs or views, which in turn are usually based upon even more fundamental values, but the debate is nonetheless driven and sustained by which underlying view, or even cultural predisposition, dominates.
Herein lies my question: Have people done the kind of technical investigation we are describing? I don’t think they have. Maybe they haven’t because tools that would enable it have yet to be adequately developed (I think cross-impact balances are a promising start). Hopefully technical people don’t talk themselves out of even trying such a study because they perceive value/belief arguments as ‘hopelessly distant’ from the clear thinking that underlies, say, mathematics.
Part of the power (and danger) of rhetorical arguments is that it’s easy to stitch together associations, even when they aren’t relevant. When attached to enough ethos and pathos, even terribly weak logical arguments can manage to persuade a lot of people.
Vanessa wrote:
I don’t know whether the technical investigation you were describing had exactly been done in the same way, but there are tools which are somewhat similar and the mathematical part is at least to some extend rather well studied. A traditional tool which comes immediately into my mind is the game ecopolicy which started out with the 34 year old cardboard game Ökolopoly. There is a whole class of games called `serious games’, which investigate at least partially similar aspects, like the BBC climate game, which I already mentioned to Alastair or others. I am writing infrequently about games on our blog and I am currently writing on and off amongst others about using MMOGs for testing uncharted political and economic scenarios. Some excerpts of this article are also scattered on Azimuth. I recently got a little further apart from the games aspect, because I felt that other things had to be investigated first, apart from this I can’t devote too much time to this project. I also think that it needs a kind of “slow approach” and it may eventually never be “finished”.
On the mathematical side I had tried to explain above that the CIB with Alastair’s example matrix seems to behave similarly to multiplication (from the right) with a certain positive “blockwise stochastic” matrix. These kind of matrices have been rather well investigated and eventually things like that might help to study equilibria, but I am not an expert for this.
I fear this is not only true for rhetorical arguments but it is however often also not so easy to tell what’s relevant oi the first place.
Oh yes it seems logos is a highly controversial term with discussions from ancient times reaching into nowaday’s world, which manifest itself for example in the investigation of
Justin Martyr’s Use of ‘Logos Spermatikos’ And The 21st Century Task (abstract in the preview).
And coming back to the associations—the interesting thing about the use of emotions in reasoning (like with ethos and pathos) is that it actually usually rather furthers the reduction of the number of possibly to be followed associations.
Vanessa, you may also find a “brimming toolkit” for forcasting at the Institute for the Future.
I haven’t much looked at this though and one should bear in mind that according to Wikipedia:
By the way coming back to the above mentioned game ecopolicy, eventually you find that interesting. There is actually a kind of tradition of “ecopolicy olympic games” According to the website three of their main side-sponsors was Berlin’s sanitation department.
Alistair wrote:
At least it seems that the historical development actually startet out with conditional probabilities in the socalled cross impact analysis or method . The method was used in the card game “Future”, which was a promotional gift offered by the Kaiser Aluminum and Chemical Company in the mid 1960. The “impact coefficients” where rather thought as a perceptionally easier access to judgements (at least thats how I interprete it). That is in this description of the history of the socalled “cross impact method” (CIM) by Theodore Gordon it is written:
Nad, you are correct that cross-impact analysis (CIA) is a probabilistic method that pre-dates cross-impact balances (CIB). As a graduate student, something that I noticed when looking at a CIA study for a system that had been ‘translated’ into a CIB version is that CIA found fewer basins of attraction compared to CIB (at least for the study I examined). It appeared that this happened because of the conditional probabilities. For low-probability states of factors, CIA would converge too quickly to a scenario being deemed impossible, while CIB could find ‘improbable’, but nevertheless self-consistent (or nearly self-consistent), basins. Such basins may precisely be the ones that should concern us most, since out of sight is out of mind (and a contingency not prepared for).
John commented earlier that he thought probability theory could be helpful for these Markov chains of social change that Alastair, I, and colleagues are toying with. I am open to this suggestion, but I also wonder if not using probabilities (or a careful choice of when to employ probabilities) can have benefits of its own.
Business people might be interested in the math of “optimal capital budgeting.”
As well as the logic of optimal capital budgeting.
Mathematical research into accounting would have to be the study of natural language.
In addition, mathematical researchers studying accounting must be able to describe information systems and have some way to reason about optimal budgeting.
The idea was optimality in a budget, formally described, depends on formally specifying impossible and possible information systems about cost.
In this game, before the player can move to the square of optimality in budgeting, she first must reach the square of optimality in available information.
In the history of accounting research, these abstract specifications of ideal mathematical costing systems were called “activity based costing” and “workpoint costing.”
Given perfect information about activities and workpoints, the possibility of an optimal budget would exist. But if the information about these costs is imperfect, then the optimal budget is impossible.
Thus enters the logic involved in optimal capital budgeting.
I think I would have to begin by clarifying “activity based costing,” clarifying “workpoint costing” in this context, then how the workpoint is a “situation” in situation theory, and finally how this situation is a point that’s being typed in Homotopy Type Theory. Here’s a proposal of how I could proceed. If this is of interest, I can expand with more detailed references. Just let me know!
The “activities” in activity based costing are transitions in the kind of Petri net I use in that paper about factory simulation I posted. While in situation theory, activities are the relations which are expanded into “infons” or elements of information in situation theory. This idea was taken into workplace anthropology by Lucy Suchmann in her book “Plans and Situated Action”– every action is situated in a situation. Likewise, every activity in activity-based costing occurs within the context of a situation in situation theory.
A situation is just a model from model theory that can itself be the constituent of a proposition the model supports. This produces circularity, as studied in the book by Barwise and Moss titled “Vicious circles.”
Barwise once wrote a paper in which the situation was a point, and the elements of information were sets having that point as an element in a kind of topology. It’s like the point being typed in Homotopy Type Theory. In the situation theory literature, it is also said that “situation supports such and such an infon” really means “the situation is of such and such a type.” Just as it might be said in Homotopy Type Theory.
It could be the abstract of a specification document for the people’s balance sheet, output from a program of workshops in the mountains somewhere.
Vanessa wrote:
I looked only briefly at the CIA methodology, so I might be wrong, but as I understood it the conditional probabilities are ranging there over all states at once rather then over each separate descriptor state space, which is rather the case for this probabilistic version of this matrix with Alastair’s constraint. That is on page 7 in the description you find a Figure 1 which is called cross impact probability matrix, upon browsing the document I couldn’t find quickly a description of Figure 1, but it seems (comparing with the description of the German wikipedia entry that a matrix entry for this matrix in Figure 1 is that is the conditional probability of event j given event i. In particular if one performs a matrix multiplication with a vector which is a probability distribution on all events then one obtains (by the law of total probability) the probability of event j and hence the outcome is again a probability distribution.
that is the conditional probability of event j given event i. In particular if one performs a matrix multiplication with a vector which is a probability distribution on all events then one obtains (by the law of total probability) the probability of event j and hence the outcome is again a probability distribution.
You may interpret the “transition coefficients” which I described above for the probability transformed CIB matrix with Alistairs constraint as conditional probabilites for a descriptor space. That is here one has a probability destribution on each descriptor space. May be thats one reason. The strange projection onto the largest state, as has been described for the CIB analysis, may be another reason.
One can do of course a lot of things. See also here.
For comparing things it may however be eventually useful to define some standards.
I don’t know what John has in mind. If I recall correctly he was also speaking of the matrix coefficients as being correlations, I don’t know how he would want to define a Markov chain with this.
I wrote:
Let me explain a bit more what I mean. It looks as if in the article is an estimated conditional probability, if you would have the precise conditional probability and if your probabilities are fully given by the given events (which is of course not always a realistic assumption) then upon matrix multiplication you should get back the original distribution, i.e. if you would regard this as a Markov chain you would have an “equilibrium”. In the article a procedure for iteratively estimating new conditional probabilities and as it seems also for the distributions themselves is given. I do not have the time to check this procedure and just briefly glanced at it, but I guess that it converges to a equilibrium. With my above link to the Perron Frobenius theorem I just wanted to indicate that I think that there are methods with which one could find an equilibrium solution for a given (estimated) conditional probability matrix, it may eventually be interesting to compare the methods. I would like to point out that this is just a handwaving argument, in particular I am definitely not an expert in probability theory.
in the article is an estimated conditional probability, if you would have the precise conditional probability and if your probabilities are fully given by the given events (which is of course not always a realistic assumption) then upon matrix multiplication you should get back the original distribution, i.e. if you would regard this as a Markov chain you would have an “equilibrium”. In the article a procedure for iteratively estimating new conditional probabilities and as it seems also for the distributions themselves is given. I do not have the time to check this procedure and just briefly glanced at it, but I guess that it converges to a equilibrium. With my above link to the Perron Frobenius theorem I just wanted to indicate that I think that there are methods with which one could find an equilibrium solution for a given (estimated) conditional probability matrix, it may eventually be interesting to compare the methods. I would like to point out that this is just a handwaving argument, in particular I am definitely not an expert in probability theory.
The Perron–Frobenius theorem indeed implies that any discrete-time Markov chain on a finite set of states has an equilibrium state. It’s Exercise 8.0.33 here:
• Caroline J. Klivans, Discrete Mathematics, Chapter 8 – Finite Markov chains.
but it’s an easy exercise based on earlier exercises.
I gave the proof of a similar result for continuous-time Markov processes in Part 23 of the network theory series. Unfortunately I only proved it for weakly reversible ones (where when it’s possible to go from one state to another, it’s possible to go back in a series of steps) which are irreducible (where you can go between any two states), because this is all I needed. However, it’s true in general, and when I finish writing the book based on these notes I should give the general proof.
I agree with this line of thinking. I’m not worried about the fact that the numbers are merely estimated conditional probabilities; experts do their estimates and we, the mathematicians, can temporarily pretend their estimates are correct. I’m worried about the meaning of these conditional probabilities.
are merely estimated conditional probabilities; experts do their estimates and we, the mathematicians, can temporarily pretend their estimates are correct. I’m worried about the meaning of these conditional probabilities.
If we start with a Markov chain we can say is the probability that our system will be in the ith state at the (n+1)st time step, given that it’s in the jth state at the nth time step. This is a conditional probability, and I understand what it means.
is the probability that our system will be in the ith state at the (n+1)st time step, given that it’s in the jth state at the nth time step. This is a conditional probability, and I understand what it means.
However, in the stohastic cross-impact balance method we probably shouldn’t regard these time steps as actual steps of time in the real world! We are not trying to predict the future and claiming the future will converge to some equilibirum probability distribution of states. Instead, the numbers mean something like the probability that we’re in the ith state now given that we’re in the jth state now. And here I say ‘something like’, because what I said barely makes sense. All I really know is that we’re looking for a probability distribution
mean something like the probability that we’re in the ith state now given that we’re in the jth state now. And here I say ‘something like’, because what I said barely makes sense. All I really know is that we’re looking for a probability distribution  with the property that
with the property that
This is our equilibrium probability distribution. But I don’t exactly know what this equation is supposed to mean!
I thought that the theory could be simple:
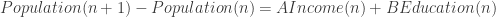
so that the Target variations (and not the target) are caused from the Influences.
The parameters could be an expert estimates, and the Vanessa Schweizer matrixes represent (with different colors) somethings like the graphical representation of a partial derivatives values (it can be a method to condense in a graph the Markov chain, or each numerical graph).
In such way a numerical trend is possible: if there is a great partial derivative then the economist, or metereologist, can try to modify these variables.
Domenico wrote:
This sort of equation is simple, but my question is: what does the variable n mean? In the comments to this post and also Part 2 we’ve seen lots of reasons why we should not think of this variable as ‘time’.
Most importantly, the experts are not being asked “how will the present value of one variable affect another variable next year?” (or some other time step). They’re being asked “how does the present value of one variable directly affect another variable now?”
So, as I’ve argued before, we should not think of the variable n as ‘time’, but rather, as a more abstract ‘relaxation parameter’:
But this doesn’t fully answer the question of what the parameter n really means—nor what the transition probabilities in the Markov chain mean! The problem is, it’s not completely clear (to me) what it means to ask “how does the present value of one variable directly affect another variable at the same time?”
John said: “However, in the stohastic cross-impact balance method we probably shouldn’t regard these time steps as actual steps of time in the real world!”
In the PDF nad is referring to, that certainly seems to be the case. The steps (I wouldn’t call them time steps even) are more like successive refinements of estimates of the . The numbers
. The numbers  are supposed to achieve the refinement. The updating is not linear as far as I can see, so the equilibrium, if there is one, may not satisfy your equation.
are supposed to achieve the refinement. The updating is not linear as far as I can see, so the equilibrium, if there is one, may not satisfy your equation.
I am thinking that if
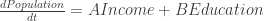


and the expert give the parameters of the model, then the evolution can be estimated.
For infinitesimal time the differential equation evolution becomes a Markov chain with some parameters constraint (to preserve the normalization), and the transition matrix is almost diagonal:
So that each almost diagonal Markov chain is an approximation of a differential equation.
Graham wrote:
It took me a second to be sure you meant: it certainly seems to be the case that we shouldn’t regard these ‘time steps’ as actual steps of time in the real world.
Okay, we agree.
Domenico wrote:
Actually this model you wrote down is a deterministic differential equation, not a Markov chain describing the evolution of probabilities with time.
But anyway, I’m not interested in this model right now; I’m interested in the setup that Vanessa Schweizer and Alastair Jamieson-Lane described in their blog posts. And I think most of us agree that their setup does not describe how quantities change with time. It describes relationships between probabilities at a fixed time.
My question remains: precisely what sort of relationship between probabilities does it describe? The equation is simple enough:
But the meaning of this equation, and how you get experts to provide estimates of the quantities is less clear.
is less clear.
Excuse me, just nonsense.
Only with probabilistic variables work.
John wrote:
I am not sure wether we are looking for that. That is I try to make sense of the whole thing just like you. In particular
I wrote:
By looking at Figure 1 the initial probabilities however do not sum to one, so eventually the authors had something else in mind, but maybe the same is meant upon rescaling. One would need to investigate this a bit more. In particular I wrote that the authors seem to use a different method.
John wrote:
If one would start out with a probability distribution then I could imagine that one could start with a “bold assumption” like that event 1 occurs with certainty and all other events do not occur and then finding an equilibrium means that one finds a distribution which is compatible with the given conditional probabilities in the matrix.
The following text (page 4) sounds a bit in that direction apart from the fact that instead of probability 1 one takes a number between $0$ and $1$, if I understand correctly:
You might be interested to take a look at Cognitive Maps, or System Dynamics approach too. However, the theoretical limit of these approaches is when you are defining those descriptors or features of the real phenomena. If we define complexity as a function of number of descriptors, then these approaches regardless of the original ideas, become arbitrary as you cannot validate the descriptors, except those cases that you use this method for communication and cross-learning. This underlying problem is “the curse of dimensionality”.
However, I am fan of Markov, and if you refer to his original idea in linguistics, he doesn’t have this dimensionality problem. In my opinion, Markov was aware of this problem and what he proposes is not a method for inference, but a method for “encapsulation of all the potential descriptors” in “symbolic relations.”