joint with Richard Elwes
Sometimes you can learn a lot from an old piece of clay. This is a Babylonian clay tablet from around 1700 BC. It’s known as “YBC7289”, since it’s one of many in the Yale Babylonian Collection.
It’s a diagram of a square with one side marked as having length 1/2. They took this length, multiplied it by the square root of 2, and got the length of the diagonal. And our question is: what did they really know about the square root of 2?
Questions like this are tricky. It’s even hard to be sure the square’s side has length 1/2. Since the Babylonians used base 60, they thought of 1/2 as 30/60. But since they hadn’t invented anything like a “decimal point”, they wrote it as 30. More precisely, they wrote it as this:

Take a look.
So maybe the square’s side has length 1/2… but maybe it has length 30. How can we tell? We can’t. But this tablet was probably written by a beginner, since the writing is large. And for a beginner, or indeed any mathematician, it makes a lot of sense to take 1/2 and multiply it by to get
.
Once you start worrying about these things, there’s no end to it. How do we know the Babylonians wrote 1/2 as 30? One reason is that they really liked reciprocals. According to Jöran Friberg’s book A Remarkable Collection of Babylonian Mathematical Texts, there are tablets where a teacher has set some unfortunate student the task of inverting some truly gigantic numbers such as 325 · 5. They even checked their answers the obvious way: by taking the reciprocal of the reciprocal! They put together tables of reciprocals and used these to tackle more general division problems. To calculate they would break
up into factors, look up the reciprocal of each, and take the product of these together with
. This is cool, because modern algebra also sees reciprocals as logically preceding division, even if most non-mathematicians disagree!
So, we know from tables of reciprocals that Babylonians wrote 1/2 as 30. But let’s get back to our original question: what did they know about ?
On this tablet, they used the value
This is an impressively good approximation to
But how did they get this approximation? Did they know it was just an approximation? And did they know is irrational?
There seems to be no evidence that they knew about irrational numbers. One of the great experts on Babylonian mathematics, Otto Neugebauer, wrote:
… even if it were only due to our incomplete knowledge of the sources that we assume that the Babylonians did not know that
had no solution in integer numbers
and
, even then the fact remains that the consequences of this result were never realized.
But there is evidence that the Babylonians knew their figure was just an approximation. In his book The Crest of the Peacock, George Gheverghese Joseph points out that a number very much like this shows up at the fourth stage of a fairly obvious recursive algorithm for approximating square roots! The first three approximations are
and
The fourth is
but if you work it out to 3 places in base 60, as the Babylonians seem to have done, you’ll get the number on this tablet!
The number 577/408 also shows up as an approximation to in the Shulba Sutras, a collection of Indian texts compiled between 800 and 200 BC. So, Indian mathematicians may have known the same algorithm.
But what is this algorithm, exactly? Joseph describes it, but Sridhar Ramesh told us about an easier way to think about it. Suppose you’re trying to compute the square root of 2 and you have a guess, say . If your guess is exactly right then
so
But if your guess isn’t right, won’t be quite equal to
. So it makes sense to take the average of
and
, and use that as a new guess. If your original guess wasn’t too bad, and you keep using this procedure, you’ll get a sequence of guesses that converges to
. In fact it converges very rapidly: at each step, the number of correct digits in your guess will approximately double!
Let’s see how it goes. We start with an obvious dumb guess, namely 1. Now 1 sure isn’t equal to 2/1, but we can average them and get a better guess:
Next, let’s average 3/2 and 2/(3/2):
We’re doing the calculation in painstaking detail for two reasons. First, we want to prove that we’re just as good at arithmetic as the ancient Babylonians: we don’t need a calculator for this stuff! Second, a cute pattern will show up if you pay attention.
Let’s do the next step. Now we’ll average 17/12 and 2/(17/12):
Do you remember what 17 times 17 is? No? That’s bad. It’s 289. Do you remember what 12 times 24 is? Well, maybe you remember that 12 times 12 is 144. So, double that and get 288. Hmm. So, moving right along, we get
which is what the Babylonians seem to have used!
Do you see the cute pattern? No? Yes? Even if you do, it’s good to try another round of this game, to see if this pattern persists. Besides, it’ll be fun to beat the Babylonians at their own game and get a better approximation to .
So, let’s average 577/408 and 2/(577/408):
Do you remember what 577 times 577 is? Heh, neither do we. In fact, right now a calculator is starting to look really good. Okay: it says the answer is 332,929. And what about 816 times 408? That’s 332,928. Just one less! And that’s the pattern we were hinting at: it’s been working like that every time. Continuing, we get
So that’s our new approximation of , which is even better than the best known in 1700 BC! Let’s see how good it is:
So, it’s good to 11 decimals!
What about that pattern we saw? As you can see, we keep getting a square number that’s one more than twice some other square:
and so on… at least if the pattern continues. So, while we can’t find integers and
with
because is irrational, it seems we can find infinitely many solutions to
and these give fractions that are really good approximations to
. But can you prove this is really what’s going on?
We’ll leave this as a puzzle in case you’re ever stuck on a desert island, or stuck in the deserts of Iraq. And if you want even more fun, try simplifying these fractions:
and so on. Some will give you the fractions we’ve seen already, but others won’t. How far out do you need to go to get 577/408? Can you figure the pattern and see when 665,857/470,832 will show up?
If you get stuck, it may help to read about Pell numbers. We could say more, but we’re beginning to babble on.
References
You can read about YBC7289 and see more photos of it here:
• Duncan J. Melville, YBC7289.
• Bill Casselman, YBC7289.
Both photos in this article are by Bill Casselman.
If you want to check that the tablet really says what the experts claim it does, ponder these pictures:

The number “1 24 51 10” is base 60 for
and the number “42 25 35” is presumably base 60 for what you get when you multiply this by 1/2 (we were too lazy to check). But can you read the clay tablet well enough to actually see these numbers? It’s not easy.
For a quick intro to what Babylonian mathematicians might have known about the Pythagorean theorem, and how this is related to YBC7289, try:
• J. J. O’Connor and E. F. Robertson, Pythagoras’s
theorem in Babylonian mathematics.
We got our table of Babylonian numerals from here:
• J. J. O’Connor and E. F. Robertson, Babylonian numerals.
For more details, try:
• D. H. Fowler and E. R. Robson, Square root approximations in Old Babylonian mathematics: YBC 7289 in context, Historia Mathematica 25 (1998), 366–378.
We also recommend this book, an easily readable introduction to the history of non-European mathematics that discusses YBC7289:
• George Gheverghese Joseph, The Crest of the Peacock: Non-European Roots of Mathematics, Princeton U. Press, Princeton, 2000.
To dig deeper, try these:
• Otto Neugebauer, The Exact Sciences in Antiquity, Dover Books, New York, 1969.
• Jöran Fridberg, A Remarkable Collection of Babylonian Mathematical Texts, Springer, Berlin, 2007.
Here a sad story must indeed be told. While the field work has been perfected to a very high standard during the last half century, the second part, the publication, has been neglected to such a degree that many excavations of Mesopotamian sites resulted only in a scientifically executed destruction of what was left still undestroyed after a few thousand years. – Otto Neugebauer.



I love the pun Dr. Baez and Dr. Elwes! Which one of you is responsible for that? Aside: are you going to have time for a doctoral student in Riverside next fall?
The advantage of writing a joint post is that neither of us has to take the blame for that pun: we can both blame each other.
I will indeed be seeking good grad students to work with me on network theory, and perhaps some topics relating to climate change and mathematical biology.
Too many ‘networks’ in this link, should be:
http://math.ucr.edu/home/baez/networks/networks.html
Thanks—I fixed it.
Hello Dr Baez,
I don’t know if you reply to posts this old, but I am looking for information on a war that was fought over the existence of the square root of two. I am a biochemist, but recall a fabulous math instructor I had a few decades ago in college making reference to this. Are you familiar with the occurrence of this in history such that you could tell me anything about it to help me research it?
I really like the breadth of topics you explore on your blog and how you facilitate the opportunity for viewers to explore the topics by working on them mathematically themselves.
Michele wrote:
To me posts never grow old; I would the discussions to go on for centuries. It’s mainly other people who lose interest.
I have never heard of a “war fought over the existence of the square root of two”, and I think I’d have heard of it if it existed.
This story could perhaps be a huge exaggeration of another story which is itself probably just a legend, about a disciple of Pythagoras who was drowned because he proved the irrationality of the square root of two. According to Wikipedia:
More Babylonian digits:
577 / 408 = 1 24 51 [10 35 17 38 49 24 42 21]
665857 / 470832 takes a long time to start repeating, so I won’t give the full list, but it starts 1 24 51 [10 7 46 6 9 12 43 0 …].
The first few exact digits are 1 24 51 10 7 46 6 4 44.
Cool! Since you seem to be good at this, could you verify that 1/2 times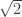 really has the sexagesimal expansion given on that tablet? All the experts say so, but I’ve been meaning to check it myself, just to feel a bit better about it.
really has the sexagesimal expansion given on that tablet? All the experts say so, but I’ve been meaning to check it myself, just to feel a bit better about it.
Also, anyone who wants to take a stab at those puzzles near the end should tell us what they come up with!
1) If we start with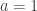 and keep averaging
and keep averaging  and
and 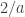 , do we keep getting fractions
, do we keep getting fractions 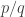 with
with
2) What about the fractions we get by expanding these:
and so on?
3) What’s the relation between the fractions in 1) and the fractions in 2)?
(1, 24, 51, 10) / 2 surely has that 42 25 35 form — it’s just standard grade school arithmetic in a larger base.
(1/2, 30 + 24 / 2, 51 / 2, 30 + 10 / 2), where the divisions round down and 30s come from odd digits above.
The first few actual digits are 0 42 25 35 3 53 3 2 22 25 43.
(I wouldn’t trust these “actual digits” very far — I’m not using arbitrary precision libraries for sqrt(2), but going through double precision floating point. I suppose I should just use the continued fraction expansion, but I’d have to dig up and modify some old code for that.)
Aaron wrote:
I know, but I didn’t like arithmetic in grade school, and I don’t like it any better in base 60.
Thanks for checking it!
I think we can show by induction that the averaging process always gives fractions of the form such that
such that  . Start with
. Start with  , which satisfies the condition. Then define:
, which satisfies the condition. Then define:
If we put , and assume that
, and assume that  , we get:
, we get:
And we have:
Nice! I knew it should be a proof by induction using just algebra, no sneaky extra tricks… but I hadn’t actually done it.
The continued fractions also have a simple recursive relationship between them. If we drop the intial 1 it’s obvious that you can get the other bit from the previous other bit just by adding 2 and inverting. If we then allow for the extra 1, we add 1 rather than 2, invert, and then add 1 again. In other words:
If we look at every second term in this sequence, we get:
If we start with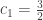 this is a fraction of the form
this is a fraction of the form  satisfying
satisfying  , and we have:
, and we have:
So by induction, every second of the continued fractions satisfies .
.
Oh, and other sub-series of the continued fractions satisfy . To prove this just add 2 to both sides of the last equation derived above, to get
. To prove this just add 2 to both sides of the last equation derived above, to get
and note that which satisfies
which satisfies  .
.
Great! So the remaining puzzle is how these two ways of getting solutions of the Diophantine equation
namely the ‘averaging’ method and the ‘continued fraction’ method, are related.
At first I naively guessed the averaging method gave all the solutions that the continued fraction method gave. But then I read about Pell numbers on Wikipedia and noticed that
arises from the continued fraction method but not the averaging method.
And then I remembered that the averaging method gives a sequence of approximations to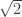 where the number of correct digits roughly doubles each time… while for continued fraction approximations to
where the number of correct digits roughly doubles each time… while for continued fraction approximations to 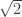 the number of correct digits grows roughly linearly.
the number of correct digits grows roughly linearly.
So, I now guess that the th solution of
th solution of
obtained by the averaging method is something like the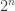 th solution obtained by the continued fraction method. But I’ve refrained from attempting to work out the details: someone else should have all the fun.
th solution obtained by the continued fraction method. But I’ve refrained from attempting to work out the details: someone else should have all the fun.
Presumably this has been known by number theorists for at least a few centuries—maybe longer! I read that Archimedes discovered some relation between approximations to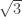 and another case of Pell’s equation, namely:
and another case of Pell’s equation, namely:
I don’t know exactly what he did, but somehow he noticed
which means that
is a good approximation to
Since Pell’s equation is a classic topic in number theory, I don’t expect to discover anything new about it. However, the approach where you start by looking for good approximations to square roots seems a lot more fun than the approach where you say “here’s a random-looking equation: let’s look for integer solutions!” So when I teach number theory next, I may talk about this. I could start by showing the students this:
and tell a nice tale, starting around 1700 BC and leading up to Pell’s equation and maybe even beyond.
If you have a solution to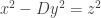 then you know that
then you know that  and
and 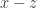 are multiples of the factors of
are multiples of the factors of  , so it’s a very interesting equation for cryptographers.
, so it’s a very interesting equation for cryptographers.
@reperiendi: could you state this a bit more formally? I’m honestly not sure what you’re trying to say.
My guess is that he was trying to say that when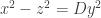 , then
, then  is divisible by
is divisible by  .
.
(By the way, ‘reperiendi’ is my student Mike Stay—that’s very easy to discover, but he usually posts here under his real name, so I thought I should mention it.)
Yes: Legendre showed that by taking the continued fraction convergents to
to  , you get that
, you get that 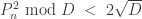 . You compute a bunch of these remainders, factor each of them and do Gaussian elimination of the squarefree part. The result is a pair
. You compute a bunch of these remainders, factor each of them and do Gaussian elimination of the squarefree part. The result is a pair 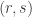 whose squares differ by a multiple of
whose squares differ by a multiple of  , so
, so 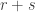 and
and  will, much of the time, share only a single factor each with
will, much of the time, share only a single factor each with  , allowing you to factor
, allowing you to factor  .
.
I wrote “only share a single factor with “—I’m assuming that
“—I’m assuming that  is the product of two large primes, since that’s how you generate the modulus for RSA.
is the product of two large primes, since that’s how you generate the modulus for RSA.
From computer calculations it’s easy to check that for the first few cases your guess is exactly right.
If we number both sequences so they start at , then
, then 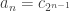 .
.
I don’t know how to prove this yet!
Ah, it’s easy to prove by induction that the continued fractions , defined with:
, defined with:
all satisfy the equation:
This is clearly true for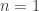 . To show that it being true for some
. To show that it being true for some  implies it for
implies it for 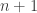 , you can just apply the recursion relations we found previously:
, you can just apply the recursion relations we found previously:
Applying the first recursion relation gives us:
Applying the second recursion relation to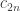 , which by the induction hypothesis equals
, which by the induction hypothesis equals  , gives:
, gives:
Hey, that’s a cool proof! Indeed, it’s not immediately clear how to show that if they’re defined recursively using
if they’re defined recursively using 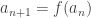 ,
,  . It seems like trying to march forward when one leg is going a lot faster than the other. That had me stuck. But you found a neat way to do it.
. It seems like trying to march forward when one leg is going a lot faster than the other. That had me stuck. But you found a neat way to do it.
If any number theorists read this, please tell us when this fact was first discovered: starting with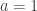 and repeatedly averaging
and repeatedly averaging  and
and 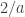 ,
,  times, gives the
times, gives the 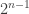 st term in the continued fraction expansion of
st term in the continued fraction expansion of 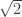 . I want to know how many more centuries I need to think about math before I catch up.
. I want to know how many more centuries I need to think about math before I catch up.
Yes, this is very nice indeed! I got as far as the algebra in Greg’s first comment, but this shows a relationship between the two sequences very clearly.
I was curious to see whether this relationship generalised to arbitrary periodic continued fractions, which are always roots of some quadratic with integer coefficients, and applying Newton’s method to solve the same quadratic.
The answer turns out to be that when things work out nicely there’s an analogous powers-of-two link, but there are other cases where applying Newton’s method to refine an approximation will give a result whose continued fraction is no longer a truncated version of the infinite continued fraction of the true result.
In the cases where everything goes nicely, suppose the quadratic root’s continued fraction has a repeating block of partial denominators of length .
.
If you define such that each of these continued fractions includes
such that each of these continued fractions includes  more partial denominators than the one before, then applying Newton’s method to any
more partial denominators than the one before, then applying Newton’s method to any  yields
yields 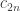 .
.
But take the quadratic:
This has roots:
The sequence of denominators for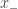 is [0;1,1,3,4,3,4,3,4,…] and the sequence for
is [0;1,1,3,4,3,4,3,4,…] and the sequence for  is [1;2,3,4,3,4,3,4,…]
is [1;2,3,4,3,4,3,4,…]
Let’s concentrate on . The first few truncated continued fractions for this are:
. The first few truncated continued fractions for this are:
Applying Newton’s method to the quadratic gives the recursion:
We can’t apply this to 1 because the denominator is zero, but if we apply it to it gives
it gives  , whose sequence of denominators is [1;2,3,2]. If we apply it to
, whose sequence of denominators is [1;2,3,2]. If we apply it to  it gives
it gives  , whose sequence of denominators is [1;2,3,4,3,2]. And if we apply it to
, whose sequence of denominators is [1;2,3,4,3,2]. And if we apply it to 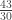 it gives
it gives  , whose sequence of denominators is [1;2,3,4,3,4,3,2].
, whose sequence of denominators is [1;2,3,4,3,4,3,2].
So the relationship almost works in general, but cases like this mean it’s not a perfect match.
Greg wrote:
Cool—thanks for figuring that out! I was wondering how much this generalized.
What are some nice examples where the relationship does work as nicely as possible? The golden ratio?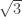 ? They both have appealing periodic continued fraction expansions. And I’m curious about how Archimedes noticed that
? They both have appealing periodic continued fraction expansions. And I’m curious about how Archimedes noticed that
though I haven’t taken the time to read what, if anything, he said.
Everything works nicely for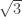 (which is [1;1,2,1,2,1,2,…]) and the golden ratio (which is [1;1,1,1,…]).
(which is [1;1,2,1,2,1,2,…]) and the golden ratio (which is [1;1,1,1,…]).
For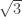 , which has a repeated block of size 2, you actually get Newton’s method doubling the index, i.e.
, which has a repeated block of size 2, you actually get Newton’s method doubling the index, i.e.
even if you list all the successive continued fractions as . With some other examples, though, such as
. With some other examples, though, such as 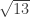 , which has a repeated block of size 5, you only get
, which has a repeated block of size 5, you only get  if you add five more denominators to each continued fraction
if you add five more denominators to each continued fraction  in the list.
in the list.
With the golden ratio, the repeated block has size 1, and Newton’s method doubles the index.
So far, all the examples I’ve seen where Newton’s method takes you out of the continued fractions list altogether have more than a single non-repeating entry at the start, e.g. [1;2,3,4,3,4,3,4…].
As for Archimedes knowing that:
for what it’s worth you can get there in two steps of the Babylonian method, if you start at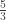 . If you start at 1 or 2 you never hit it.
. If you start at 1 or 2 you never hit it.
Nice. I like giving students pattern-finding problems in number theory, so now I can give them something where they approximate the golden ratio using Newton’s method and are forced to notice that the 2nth Fibonacci number shows up! This would come after lots of easier problems involving Fibonacci numbers…
There’s a really simple general result that lies behind these “powers of two” patterns.
Suppose you have a fractional linear function (and we rule out true linear functions):
We can normalise the coefficient of in the denominator to 1 because if it started out as zero we’d have a linear function.
in the denominator to 1 because if it started out as zero we’d have a linear function.
The fixed points of this function, where , will be roots of a quadratic:
, will be roots of a quadratic:
The successive refinements to an approximation to a root of this quadratic by Newton’s method are given by:
It turns out that, with no further assumptions at all:
which can be proved just by grinding through the algebra.
Now, if you have some sequence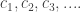 with:
with:
and it also happens to be true that:
then you have everything you need to prove by induction that:
Taking this as the induction hypothesis, we have:
Now , so what the initial condition is saying is that
, so what the initial condition is saying is that 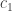 must be a root of:
must be a root of:
In other words, ruling out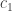 being a root of the quadratic itself, it must equal the parameter from the fractional linear transformation:
being a root of the quadratic itself, it must equal the parameter from the fractional linear transformation:
So we have the general result that in the sequence:
where:
if we use Newton’s method to refine roots of the quadratic obtained from , we will have:
, we will have:
Now we can apply this to periodic continued fractions.
With any periodic continued fraction, it’s not hard to see that adding another periodic block of denominators will amount to performing some fractional linear transformation on the number you started with. That’s why all periodic continued fractions are roots of some quadratic: the limiting value must be a fixed point of that fractional linear transformation.
When the initial non-repeating portion of the periodic continued fraction has a length of 1, we can write the transformation very simply as:
where the repeating block of denominators is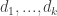 .
.
Whether we get the “powers of two” pattern will depend on whether we meet the initial condition of the induction. When the initial non-repeating portion of the periodic continued fraction has a length of 1, it turns out that this condition will always be satisfied. When the non-repeating portion is longer than 1, it generally won’t be.
Explicitly, for the case where we have a repeating block of two denominators, we have:
Here we have
which is the continued fraction with two partial denominators, and hence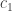 in a sequence where we add two partial denominators (the size of the repeating block) to each successive term.
in a sequence where we add two partial denominators (the size of the repeating block) to each successive term.
My gosh, Greg, this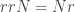 identity is beautiful and striking and cries out loud for a conceptual explanation. Do you have one? How did you find this identity?
identity is beautiful and striking and cries out loud for a conceptual explanation. Do you have one? How did you find this identity?
Todd, I found that identity because it was a necessary condition for the inductive proof of the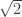 case to generalise to other quadratics.
case to generalise to other quadratics.
I don’t have a conceptual explanation for it! There might be a geometric explanation, somehow connected to the fact that:
Or maybe it’s somehow related to the group theory of fractional linear transformations, though I’m not sure how to bring into that.
into that.
Really cool stuff!
Here’s a shallow thought: we can rewrite
as
which could be more tractable since it’s always good to conjugate something by something else.
The ordinary Newton’s method involves drawing a straight line, so Newton’s method warped by a fractional linear transformation would involve drawing a circle.
Here’s a better thought.
Greg’s function is a fractional linear transformation with an attractive fixed point. Most or all transformations of that sort are conjugate, within the group of fractional linear transformations, to one of this sort:
is a fractional linear transformation with an attractive fixed point. Most or all transformations of that sort are conjugate, within the group of fractional linear transformations, to one of this sort:
for some with
with 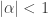 . (This transformation has the origin as an attractive fixed point.)
. (This transformation has the origin as an attractive fixed point.)
So, let’s assume we can do a change of coordinates via a fractional linear transformation so that in these new coordinates
In this new coordinate system what map would obey
would obey
The obvious choice is squaring:
So, I believe that when we change coordinates as described, will be be squaring.
will be be squaring.
And here’s another piece of evidence for this: we know that Newton’s algorithm converges quadratically, meaning that if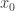 is the attractive fixed point of
is the attractive fixed point of  and
and  is some nearby point,
is some nearby point,
Squaring has the origin as a fixed point and it’s quadratically convergent in this sense.
On the other hand the original map , and multiplying by
, and multiplying by  with
with 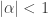 , are maps with an attractive fixed point that only converge linearly. As Greg suggested,
, are maps with an attractive fixed point that only converge linearly. As Greg suggested, 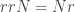 is a very reasonable relation between two maps with same attractive fixed point, one of which converges linearly and the other of which converges quadratically.
is a very reasonable relation between two maps with same attractive fixed point, one of which converges linearly and the other of which converges quadratically.
Seems to be barking up the right tree — thanks, John!
That’s brilliant, John!
If you define:
where are the roots of the quadratic, then:
are the roots of the quadratic, then:
and
where
I should have described the transformed fractional linear function in a nicer way:
This makes it crystal clear that if you start with in the original coordinates, so the sequence is:
in the original coordinates, so the sequence is:
in the transformed coordinates it becomes:
And since the Newton’s method iteration is transformed to squaring:
the reason iterating with doubles your index in this sequence becomes completely transparent!
doubles your index in this sequence becomes completely transparent!
Great! It’s nice how a mysterious fact can, with sufficient cogitation, be made crystal clear. It’s especially fun doing it as part of a team.
I’m still curious when this was first discovered. Since fractional linear transformations play a mammoth role in number theory, I can’t believe we’re the first to notice it.
John wrote:
There may be though diverging opinions about whether a team is a team.
I’m not sure what that’s supposed to mean. Is that a general observation, or you trying to hint at something in particular?
I can’t resist mentioning another technique for rational approximations that falls out of the whole fractional linear approach: if Newton’s method under the change of variables corresponds to squaring, what do higher powers give us?
Rather than work this out in all generality, what if we apply this to approximating the square root of 2 by some higher-power version of Newton’s method, and to keep things simple just start at 1 and apply a single step.
The result for even is:
is:
For odd it is:
it is:
For example, for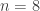 this gives us:
this gives us:
Reading about Babylonian math in 1700 BC made me want to see how far back it goes. This page was helpful:
• Duncan Melville, Third millennium mathematics.
It turns out the earliest writing in Mesopotamia goes back to 3200-2900 BC. We have 6000 clay tablets from this period, mostly from the city of Uruk. All were either found in ancient rubbish dumps or were illegally excavated and sold on the black market, so there is no archaeological context for any of them!
So, apart from the information on the tablets we know nothing about how they were used, who wrote them… or anything! That really sucks.
However, people have figured out that they’re lists of records like “3 sheep” or “5 bowls of barley”. There are no sentences, no verbs, no grammar.
But here’s the cool part: they used 3 different number systems. A base-60 system, the S system, was used to count most discrete objects, such as sheep or people. But for ‘rations’ such as cheese or fish, they used a base 120 system, the B system. And yet another system, the ŠE system, was used to measure quantities of grain. It took work to figure this out.
What about before writing?
Back in 8000 BC, they used little geometric clay figures called “tokens” to represented things like sheep, jars of oil, and various amounts of grain. Apparently they were used for contracts! Eventually groups of tokens were sealed in clay envelopes, so any attempt to tamper with them would be visible.
But, it was annoying to have to break a clay envelope just to see what’s in it. So after a while, they started marking the envelopes to say what was inside. At first, they did this simply by pressing the tokens into the soft clay of the envelopes. Later, these marks were simply drawn on tablets. Eventually they gave up on the tokens – a triumph of convenience over security. The marks on tablets then developed into the Babylonian number system! The transformation was complete by 3000 BC.
This gradual process probably explains why they used different number systems for different kinds of things before settling on the ‘abstract’ numbers around 3000 BC.
So, it took 5000 years of abstraction to get from tokens to writing and numerals! It seems slow, but of course they had other things on their mind. This reminds me a bit of how we slowly come up with better and better ways to use computers. We change things a bit at a time, in a messy sort of process.
You say:
Actually, they had something like a dozen systems. I only mentioned a few on my web page. The standard reference is:
• Nissen, H. J., Damerow, P. and Englund, R. (1993). Archaic bookkeeping : early writing and techniques of the economic administration in the ancient Near East, University of Chicago Press.
Thanks, Duncan! I think it’s fascinating that the same culture had so many number systems before they were unified. It makes me think of the proliferation of computer-related standards we see now, and the battles to simplify and unify them. I wonder if those will ever settle down as our number system did.
I think everyone interested in the history of mathematics should read your Mesopotamian Mathematics webpages! They provide just enough detail to be fascinating, not so much as to be overwhelming. That’s what makes me people want to learn more. I want to learn more!
Anyone interested in this who prefers to be overwhelmed should read Georges Ifrah’s Universal History of Numbers: http://www.amazon.com/dp/0471375683
That looks good—I’ll try to get it from the library. When it comes to absorbing truly large amounts of information, I prefer an old-fashioned book to a webpage. I guess one reason is simply that it sits there, physically reminding me of its existence, so I keep going back to it. (I don’t have a Kindle-oid yet.)
Here’s another fun fact:
The first known math homework in Mesopotamia—and maybe in the world?—goes back to about 2500 BC. It involves dividing by 7. Given that base 60 makes it easy to divide by 2, 3, 4, 5, and 6, this proves that math teachers have always been sadists.
But the really cool part is that the same homework problem shows up on two tablets, and one of the students gets it wrong. One expert commented that it was “written by a bungler who did not know the front from the back of his tablet, did not know the difference between standard numerical notation and area notation, and succeeded in making half a dozen writing errors in as many lines.” This proves that grading homework has always been depressing.
This is from
• Duncan Melville, Early dynastic mathematics.
Sweet historical analysis.
The Babylonians had a very fortuitous choice of writing material for such a war-torn region. It had the property that when the city was razed, the library contents were preserved (clay+fire->ceramic).
Subsequent choices, papyrus, parchment and paper, all burn.
That’s a nice point. I’ve read that data storage media have been getting more and more perishable ever since people switched from carving on rock to the convenience of clay tablets.
It would be great if all the Babylonian clay tablets had been baked into indestructible ceramic. Unfortunately it seems not. Here is a tragic passage from Neugebauer:
That’s the back story behind the quote at the end of the blog article:
It’s a bit of a digression, but here’s some more about the preservation of knowledge from Stewart Brand. This is his summary of Brewster Kahle’s recent talk at the Seminars on Long Term Thinking:
I don’t think you mentioned it explicitly, but this iterative averaging method of computing square roots is equivalent to Newton’s method. (It’s also how I used to compute square roots as a kid on calculators that didn’t have square root buttons.)
Yes, that’s a good thing to note. Of course Newton’s method is a lot more general, and in general it uses calculus:
When pondering Babylonian mathematics one wants to come up with ways they could have guessed the special case of Newton’s method for computing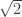 without knowing calculus—that’s why I didn’t mention Newton’s method.
without knowing calculus—that’s why I didn’t mention Newton’s method.
George Gheverghese Joseph gives a way that doesn’t quite mention calculus, but comes very close. It goes like this:
Suppose you want to know the square root of and you already have an approximate answer, say
and you already have an approximate answer, say  . You want to find a better approximation, say
. You want to find a better approximation, say  . You note that
. You note that  if
if 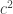 is small. So, you set
is small. So, you set  and solve this for
and solve this for  . Then
. Then  is your new better approximation.
is your new better approximation.
But if you work out what is, it’s just the average of
is, it’s just the average of  and
and 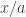 . And that seems like an idea people could have invented without the rigamarole I just described.
. And that seems like an idea people could have invented without the rigamarole I just described.
I don’t yet have enough of a sense yet of how the Babylonians thought about this stuff. I should read this more carefully:
• D. H. Fowler and E. R. Robson, Square root approximations in Old Babylonian mathematics: YBC 7289 in context, Historia Mathematica 25 (1998), 366–378.
I think it should shed some light on it.
I came across a very nice and natural geometric interpretation of that averaging algorithm. You are finding a square root of A by constructing a sequence of rectangles of a fixed area A, which converge to the square of area A. In each step, you average the previous two side-lengths to get one of the sides, and the other one is, naturally, A/guess. Don’t remember the source, sorry.
Newton’s method converges much more quickly than the method I use for extracting square roots in my head, a relaxing mental exercise useful when, for example, stuck in traffic. On the other hand, my method is in decimal, so I can sit there and recite digits (more and more slowly, as my mental scratchpad gets fuller). And I was taught it by my mother, so it serves as a memorial exercise too.
Let me see if I have your argument right.
There is a simple algorithm which at each iteration gives you better approximations of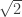 . The third iteration after the initial choice of 1 is 577/408. This fraction worked out to three places in base 60 is the same as the Babylonian expression for
. The third iteration after the initial choice of 1 is 577/408. This fraction worked out to three places in base 60 is the same as the Babylonian expression for 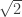 . Therefore, it’s reasonable to think the Babylonians used (something like) this algorithm.
. Therefore, it’s reasonable to think the Babylonians used (something like) this algorithm.
That’s quite a piece of Peircean abduction. I’m not sure I see that we can say much more than that they must have had some method which approaches to the true value. It might have been as clumsy as trial and error: if too high/low, try lower/higher. So long as they had some means of getting nearer to the correct value, if they had the patience, they were always going to be able to achieve three place base 60 accuracy.
Whoops. It’s not really ‘our argument’, it’s the conventional wisdom. I could try to pull the wool over your eyes and note that Wikipedia calls the recursive algorithm I described the Babylonian method. I could point out lesson plans that say things like:
However, I have not yet seen anyone go further than to say it seems plausible that the Babylonians might have computed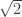 this way. And indeed the Wikipedia article has a little footnote saying:
this way. And indeed the Wikipedia article has a little footnote saying:
So, you’ve got a great point, and I should reword the article (at least the version on my website). But first I’ll re-read this more carefully:
• D. H. Fowler and E. R. Robson, Square root approximations in Old Babylonian mathematics: YBC 7289 in context, Historia Mathematica 25 (1998), 366–378.
They describe some other Babylonian calculations, which might give us a better sense of what they were likely to have done.
Here’s a nice example from Fowler and Robson, taken from an old Babylonian tablet:
This takes a while to understand! If you’re anything like me, your first impulse is to think about something else: it looks difficult yet boring at the same time.
But let me lead you all through it.
First, we need to know that a rod is 12 cubits. Second, we need to know how scholars of Babylonian mathematics write numbers in base 60. The semicolon is a ‘decimal point’ (or ‘sexagesimal point’), which is not actually present in the clay tablets—it’s the result of guesswork. But let’s not worry about that; the idea is that 0;01 40 is short for
and so on.
So, let me translate:
It’s easier to understand if we abstract the idea using algebra:
I’d call this a first-order Taylor series approximation:
It’s good when is much smaller than
is much smaller than  . Of course we can’t be sure what they thought they were doing!
. Of course we can’t be sure what they thought they were doing!
For this gives us 3/2 as an approximation to
this gives us 3/2 as an approximation to 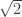 —not very good, since
—not very good, since  isn’t much smaller than
isn’t much smaller than  .
.
But anyway, they start here and study some possible ways that tricks along these lines could led the Babylonians to much better approximations of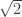 .
.
David wrote:
That’s true. But I guess on the basis of example like the one I just described, most scholars of Babylonian mathematics think of the Babylonians as fairly clever, not clumsy plodders. And they try to make up stories that seem consistent with what they know the Babylonians could do.
But it seems we’ll never know for sure. There are probably lots of clay tablets still buried that could help us out—and lots that have been dug up but haven’t been translated, and many that have been sitting in moist European museums for so long that it’s too late! (See my reply to Roger Witte.)
I’ll stand by this post as being a) plausible, and b) in line with the opinions of people who know this stuff better that I do.
But it is worth admitting that “conventional wisdom” on Babylonian mathematics can be wrong, and does change. It was conventional wisdom for several years that Plimpton 322 was a table of Pythagorean triples. But Eleanor Robson put paid to this idea in 2001, acidly remarking that “Ancient mathematical texts and artefacts, if we are to understand them fully, must be viewed in the light of their mathematico-historical context, and not treated as artificial, self-contained creations in the style of detective stories.”
Click to access neither-sherlock.pdf
I don’t think we fell into the Sherlock Holmes trap here, but it certainly is worth watching out for!
Sorry to comment on an ancient post, but I see this interpretation of Robson repeated again and again, and it frustrates me. Plimpton 322 can’t literally be a table of Pythagorean triples, not least because it only contains one of the sides and the diagonal, rather than both sides and the diagonal. But are you claiming that the author of the tablet didn’t think of the numbers it contains as having to do with exact side lengths of right triangles (or of rectangles with their diagonal)? I don’t think Robson’s article supports that. I can’t think of any scholar who says that—even Friberg, who states in his book A Remarkable Collection of Babylonian Mathematical Textsthat the numbers in columns 2 and 3 shouldn’t be thought of as integer side lengths, still thinks the tablet is connected with right triangles.
It’s an ancient post, but still brand-new compared to what it’s discussing. Thanks for adding your wisdom! I don’t know about Richard, but my knowledge on this topic is very superficial and prone to mistakes.
I find the use of irrational square roots and antique versions of continued fraction expansions as rhetorical model interesting, e.g. for Platon’s dialoges, and as model for the human mind. Heraclit’s proportions like “god:man=man:child” look like that. But only if their “paradigm” were that “gods”, “childs” etc. are well known, static ideas. Like the “docta ignorantia” or “coincidentia oppositorum”, which was used by christian theologists to characterize the possible knowledge of “god” – only with the roles of “god” and “human” interchanged. If that guess is roughly correct, it would rhetorically explain why the ancient greeks saw the human mind as inherently dynamic entity, on which idea later gnostics relied.
There have been other interesting cases where concepts from mathematics suddenly became into a strong resonance with the “Zeitgeist” and it’s problems. E.g. this, written by a french anarchist in prison who had only access to math. physics books, was taken by W. Benjamin as core text for understanding the 19th century mentality (and probably influenced Nietzsche). A more recent case were the problems with set theory and the concept of functions in general ca. 100 years ago, as told in this very interesting book (video lecture, free copy).
Hmmm… no-one has mentioned harmonic means, which is interesting because they’re implicitly here, for behold:
That is, the arithmetic and harmonic mean of two numbers have the same product as those two numbers; at the same time,
It’s easy to see that the new difference is less than half the old, and eventually decreases quadratically.
Incidentally, it’s a fun game to apply Newton’s method to the function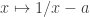 … Try it!
… Try it!
I’ll try it! I’m supposed to be writing a talk now for the CQT Symposium on Wednesday, but that means that I’m eagerly looking for various fun ways to procrastinate, inbetween bursts of activity.
Your comment on arithmetic and harmonic means reminds me of the arithmetic-geometric mean idea, which I don’t understand as well as I should… but already had floating in my mind, since it’s yet another process involving means that converges quadratically.
The idea is that you take two numbers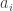 and
and  , compute their arithmetic mean
, compute their arithmetic mean
and geometric mean
and keep iterating. You can use this trick to efficiently compute elliptic integrals, and there’s a book:
• Jonathan Borwein, Peter Borwein, Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity, John Wiley & Sons, Inc., New York, 1998.
which contains some cool results. Unfortunately it’s been years since I looked at it, so I completely forget what those results are! Now I’m really curious.
Does anyone know what cool stuff is in this book? I think it contains some nice algorithms for computing π, which roughly double the number of correct digits each time. Unfortunately the Babylonians didn’t know these!
You may find this (or this continuation) interesting too.
This short note by Dan Grayson is interesting too.
Thanks! I remember reading the first one once before, but it was very good to reread it. Perhaps the strangest and most interesting part had nothing to do with the arithmetic-geometric mean: it was how much math research appeared in a British magazine called the Ladies Diary, and the story surrounding this.
There was a great exhibition of Babylonian clay tablets including YBC7829 at the Institute for the Study of the Ancient World at New York University:
• Before Pythagoras: the culture of Old Babylonian mathematics, November 12, 2010 – January 23, 2011.
which alas I missed… but a nice reading list is still available!
A very interesting post! I wonder whether ancient people knew that there were infinitely many Pell numbers?
Thank you very much!
prime
Wikipedia says:
We see a lot of papers and talk about ancient Babylonians exactness of calculating the value of square root of 2. But how close could they come to the square root of 3? […]
[…] Babylon and the Square Root of 2 | Azimuth – Dec 02, 2011 · The Babylonians knew an amazingly good approximation to the square root of 2 back around 1700 BC. But did they know it was just an approximation?… […]
Really amazing and interesting; but how do such manipulations look in alphabetical numeration or numeral systems like the Greek numerals?
I don’t know.
Why is p^2 = 2q^2+1?
3^2=2(1^2)+1?
9=3?
Can see how p represents the numerator and q the denominator but why is it different in the first equation above where you used 1^2 instead of 2^2? Just what is p^2=2q^2?
Can someone please explain this in simpler terms? Been thinking for over an hour.
David Lie wrote:
We’re trying to calculate the square root of two. If the square root of two were a rational we could find and
and  with
with
or in other words
But the square root of two is not rational! So we can’t get But we can come close: we can find integers
But we can come close: we can find integers  and
and  with
with
An easy example is
(You caught a typo in my post: I wrote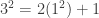 , which is nonsense. I’ll fix it now. Thanks!)
, which is nonsense. I’ll fix it now. Thanks!)
The wonderful trick is then to take one solution of
and use it to get another, bigger solution—which gives a better approximation to the square root of two!
Part of the nice thing here is visualizing this geometrically. The graph of is a hyperbola in the
is a hyperbola in the 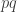 -plane, with asymptotes
-plane, with asymptotes  . If you can find a pair
. If you can find a pair  of positive integers which are coordinates of a point way way out on the hyperbola, then necessarily that point will be close to an asymptote, making
of positive integers which are coordinates of a point way way out on the hyperbola, then necessarily that point will be close to an asymptote, making 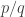 is an excellent approximation to
is an excellent approximation to 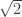 .
.
The question then is how we get such integer points way way out on the hyperbola? This is the second beautiful idea that John alluded to: exploit a group structure on the hyperbola. If I can make an analogy: the graph of
way way out on the hyperbola? This is the second beautiful idea that John alluded to: exploit a group structure on the hyperbola. If I can make an analogy: the graph of 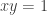 is also a hyperbola, with asymptotes given by the
is also a hyperbola, with asymptotes given by the  – and
– and  -axes. It is also a group, where two points
-axes. It is also a group, where two points 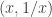 and
and 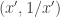 on the hyperbola may be “multiplied” in an evident way to yield a third point on the hyperbola,
on the hyperbola may be “multiplied” in an evident way to yield a third point on the hyperbola,  . Then starting with a point like
. Then starting with a point like  , repeated powers
, repeated powers 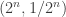 bring us closer and closer to an asymptote (the
bring us closer and closer to an asymptote (the  -axis for positive
-axis for positive  , and the
, and the  -axis for negative
-axis for negative  ).
).
Similarly, we may start with the hyperbola . Factoring it as
. Factoring it as 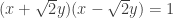 to liken it more to
to liken it more to 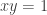 , we can multiply two points on the hyperbola. Here goes: we have
, we can multiply two points on the hyperbola. Here goes: we have
This suggests that the product of two points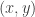 and
and 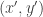 on the hyperbola should be
on the hyperbola should be
And indeed this third point lies on the hyperbola, because
Note that if are integers, then so is
are integers, then so is 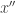 and
and  . Thus, if we start with an integer pair
. Thus, if we start with an integer pair  lying on the hyperbola, then we can take “powers” according to this product law. So the square is
lying on the hyperbola, then we can take “powers” according to this product law. So the square is
The cube is
Already is not a bad approximation to
is not a bad approximation to 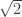 !
!
Very nice, Todd! I hadn’t thought of it in terms of a group structure on the hyperbola. There’s also a group structure on the circle that allows us to multiply two rational solutions of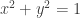 and get another, thus giving a recipe for getting new Pythagorean triples from old ones. I don’t know how interesting this is… l’m having trouble with some calculations that should be easy. Probably not awake enough yet. So I just have some questions:
and get another, thus giving a recipe for getting new Pythagorean triples from old ones. I don’t know how interesting this is… l’m having trouble with some calculations that should be easy. Probably not awake enough yet. So I just have some questions:
1) Is your group structure on the hyperbola just another ‘real form’ of the group structure on the circle? If so, what’s the complex form of this algebraic group?
2) There’s a famous old way to get new Pythagorean triples from old: you take your triple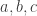 , get a point on the circle
, get a point on the circle 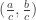 , and draw a straight line from
, and draw a straight line from 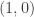 to this point. The line intersects the circle at another point with rational coordinates, and this is a new Pythagorean triple. The resulting algorithm goes back to Euclid. Is there a hyperbolic analogue of this trick?
to this point. The line intersects the circle at another point with rational coordinates, and this is a new Pythagorean triple. The resulting algorithm goes back to Euclid. Is there a hyperbolic analogue of this trick?
(The only hard part of this trick is seeing that the line intersects the circle at a point with rational coordinates, but if you write an equation for the coordinates of this point you’ll get a quadratic equation with two solutions, one being the one you want and the other coming from the point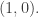 Since that other solution of the quadratic is obviously rational, so is the one you want!)
Since that other solution of the quadratic is obviously rational, so is the one you want!)
3) How is the ‘straight line’ trick related to your ‘group law’ trick?
4) There are similar famous tricks for getting new solutions of cubic Diophantine equations from old ones. These involve drawing a bunch of lines, but ultimately they rely on the fact that any elliptic curve is an algebraic group. Do these tricks reduce to either the ‘straight line’ trick or the ‘group law’ trick in some limit where a cubic degenerates to a quadratic?
Before I try to get to your questions, let me just say part of what’s going on is that we are dealing with algebraic number fields like![\mathbb{Q}[i]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BQ%7D%5Bi%5D&bg=ffffff&fg=333333&s=0&c=20201002) or
or ![\mathbb{Q}[\sqrt{2}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BQ%7D%5B%5Csqrt%7B2%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) , or the rings of algebraic integers therein like
, or the rings of algebraic integers therein like ![\mathbb{Z}[\sqrt{2}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Csqrt%7B2%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) , and we are studying the structure of multiplicative groups derived from these with the help of the norm map (taking an element
, and we are studying the structure of multiplicative groups derived from these with the help of the norm map (taking an element  in the field to the product of all
in the field to the product of all 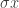 where
where 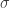 ranges over all the automorphisms of the field over
ranges over all the automorphisms of the field over 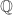 ). So the norm of a typical element
). So the norm of a typical element  in
in ![\mathbb{Q}[\sqrt{2}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BQ%7D%5B%5Csqrt%7B2%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) is
is 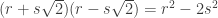 . And the norm map takes algebraic integers
. And the norm map takes algebraic integers ![p + q\sqrt{2} \in \mathbb{Z}[\sqrt{2}]](https://s0.wp.com/latex.php?latex=p+%2B+q%5Csqrt%7B2%7D+%5Cin+%5Cmathbb%7BZ%7D%5B%5Csqrt%7B2%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) to ordinary integers, and takes units of the ring
to ordinary integers, and takes units of the ring ![\mathbb{Z}[\sqrt{2}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Csqrt%7B2%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) to units
to units  . Thus we are naturally led to the group structure on the union of the two hyperbolas
. Thus we are naturally led to the group structure on the union of the two hyperbolas  .
.
Additionally, what is nice is that the group of units in![\mathbb{Z}[\sqrt{2}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Csqrt%7B2%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) , identified with certain integer pairs
, identified with certain integer pairs  , is a discrete subgroup of the two-hyperbola group (each hyperbola has two branches, so the two-hyperbola group is isomorphic to
, is a discrete subgroup of the two-hyperbola group (each hyperbola has two branches, so the two-hyperbola group is isomorphic to 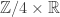 . So the group of units is finitely generated. And if we focus on just the group of integer pairs
. So the group of units is finitely generated. And if we focus on just the group of integer pairs  sitting on the branch of
sitting on the branch of  where
where  , then this branch is isomorphic to
, then this branch is isomorphic to  , so we are dealing with a discrete subgroup of
, so we are dealing with a discrete subgroup of  . But we know that discrete subgroups of
. But we know that discrete subgroups of  are either trivial or infinite cyclic! So basically we know that the solutions to Pell’s equation
are either trivial or infinite cyclic! So basically we know that the solutions to Pell’s equation  are (modulo the torsion elements
are (modulo the torsion elements  ) generated by a single element, namely the integer pair
) generated by a single element, namely the integer pair  that is closest to the identity
that is closest to the identity 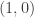 without actually being the identity. It’s easy to convince oneself that that’s
without actually being the identity. It’s easy to convince oneself that that’s  or
or 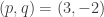 (the inverse). And the same is true for the general Pell’s equation
(the inverse). And the same is true for the general Pell’s equation  : although you have to convince yourself somehow that non-identity solutions exist, once you have one you know that you are dealing with an infinite cyclic group and you can generate all the solutions from a single solution. (Besides fancy theorems like Dirichlet’s unit theorem, the only way I know that guarantees existence of a nontrivial generator for the Pell group is by analyzing continued fraction expansions and especially their periodicity.) Oh, let me not forget to say that actually
: although you have to convince yourself somehow that non-identity solutions exist, once you have one you know that you are dealing with an infinite cyclic group and you can generate all the solutions from a single solution. (Besides fancy theorems like Dirichlet’s unit theorem, the only way I know that guarantees existence of a nontrivial generator for the Pell group is by analyzing continued fraction expansions and especially their periodicity.) Oh, let me not forget to say that actually  is the square of
is the square of  which sits on the other hyperbola
which sits on the other hyperbola  , so actually it’s
, so actually it’s  which generates the group of units in
which generates the group of units in ![\mathbb{Z}[\sqrt{2}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Csqrt%7B2%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) , modulo its torsion subgroup.
, modulo its torsion subgroup.
Okay, onto your questions now!
As for (1): you may have to help me a bit because I am not on intimate terms with the terminology. I think what we are dealing with is the group of units in the algebra![\mathbb{R}[\sqrt{D}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BR%7D%5B%5Csqrt%7BD%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) , dealing with cases like
, dealing with cases like 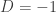 and
and  . (Or elements of norm 1, depending on what we want to look at.) The uniform group law can be written as
. (Or elements of norm 1, depending on what we want to look at.) The uniform group law can be written as
If I understand the question, it’s whether the complexified versions of the norm 1 groups are isomorphic, and the answer has to be ‘yes’ since for every nonzero , the algebra
, the algebra ![\mathbb{C}[\sqrt{D}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BC%7D%5B%5Csqrt%7BD%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) is isomorphic to
is isomorphic to  , and the norm 1 group corresponds to
, and the norm 1 group corresponds to  . I think. (But let me know if that’s not what you’re asking.)
. I think. (But let me know if that’s not what you’re asking.)
As for (2), I think you are alluding to the stereographic projection trick. In the case of a circle, we take a point like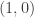 on the circle and draw the straight line between that and another point
on the circle and draw the straight line between that and another point  and watch where that line intersects a line like
and watch where that line intersects a line like  . Of course by point-slope it hits it at a point
. Of course by point-slope it hits it at a point  where
where  is rational if
is rational if  is. But conversely, if
is. But conversely, if  is rational, then the line connecting
is rational, then the line connecting  to
to 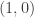 intersects the circle
intersects the circle 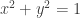 in two points. Obviously one of those points is
in two points. Obviously one of those points is 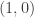 . Then we argue that the other point must have rational coordinates — essentially because if a rational quadratic polynomial has one rational root, then the other root must be rational as well, by e.g. the quadratic formula. So stereographic projection sets up a bijective correspondence between rational solutions
. Then we argue that the other point must have rational coordinates — essentially because if a rational quadratic polynomial has one rational root, then the other root must be rational as well, by e.g. the quadratic formula. So stereographic projection sets up a bijective correspondence between rational solutions  to the equation
to the equation 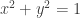 and rational numbers
and rational numbers  , and by this method we can generate all Pythagorean triples
, and by this method we can generate all Pythagorean triples 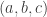 where
where 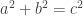 . (I wonder how old this method is? It’s not exactly Euclid’s since he didn’t have cartesian coordinates or algebraic representations AFAIK, but it’s not ridiculous to think maybe it had occurred to a 17th century mathematician…)
. (I wonder how old this method is? It’s not exactly Euclid’s since he didn’t have cartesian coordinates or algebraic representations AFAIK, but it’s not ridiculous to think maybe it had occurred to a 17th century mathematician…)
Now this stereographic projection argument is perfectly general, and so it applies to any conic with rational coordinates, such as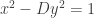 where
where  is a squarefree integer. So there is a bijective correspondence between rational points
is a squarefree integer. So there is a bijective correspondence between rational points  on this conic and rational points on the projective line
on this conic and rational points on the projective line 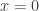 , say. After a little algebra, we see that this parametrization takes a point
, say. After a little algebra, we see that this parametrization takes a point  on the line to
on the line to 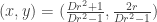 . Which is exactly how it works for Pythagorean triples, taking
. Which is exactly how it works for Pythagorean triples, taking 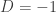 .
.
In each case we can transport the group structure on the rational conic to a group structure on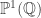 . But we get in this way nonisomorphic group structures on
. But we get in this way nonisomorphic group structures on 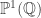 , essentially because the algebraic number fields
, essentially because the algebraic number fields ![\mathbb{Q}[\sqrt{D}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BQ%7D%5B%5Csqrt%7BD%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) have different arithmetic structures. (For example, the torsion subgroups may differ.)
have different arithmetic structures. (For example, the torsion subgroups may differ.)
Because of this, looking at (3) I’m not sure I draw that much of a connection between the group law trick and the stereographic projection trick. One can see commonalities in method when one passes to sufficiently great extensions like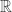 or
or 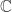 , but down here we are dealing with arithmetic which is more subtle. Note also that I was looking at elements of norm 1 in the algebraic integers
, but down here we are dealing with arithmetic which is more subtle. Note also that I was looking at elements of norm 1 in the algebraic integers ![\mathbb{Z}[\sqrt{2}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Csqrt%7B2%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) , as opposed to elements of norm 1 in the algebraic number field
, as opposed to elements of norm 1 in the algebraic number field ![\mathbb{Q}[i]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BQ%7D%5Bi%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
But, but, …
As for (4): this looks interesting! I think I’m more inclined to view the stereographic projection as referring to a group structure on the union conic + line, which forms a singular cubic. In the case we are more used to thinking about, nonsingular cubics as (unpointed) elliptic curves, the group law is prescribed by iff
iff 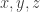 are collinear. Similarly, with stereographic projection, we are considering collineations of three points (two on the conic, one on the line). And I remember being told (this was in a brief email exchange with Noam Elkies and some others whose names I’d have to dig up) that actually group laws on eilliptic curves do pass over to group laws on even such degenerate cubics like the union of a conic and a line, or the union of three lines, although there can be a bit of weirdness going on in these degenerate siutations. Now I’m not sure right now what could be milked out of that observation, but it looks like it might be fun following up on that. (Maybe I should try to find those emails, but that could take some doing…)
are collinear. Similarly, with stereographic projection, we are considering collineations of three points (two on the conic, one on the line). And I remember being told (this was in a brief email exchange with Noam Elkies and some others whose names I’d have to dig up) that actually group laws on eilliptic curves do pass over to group laws on even such degenerate cubics like the union of a conic and a line, or the union of three lines, although there can be a bit of weirdness going on in these degenerate siutations. Now I’m not sure right now what could be milked out of that observation, but it looks like it might be fun following up on that. (Maybe I should try to find those emails, but that could take some doing…)
Thanks again, Todd! It would be really cool if the stereographic projection trick for generating new Pythagorean triples and the group structure on solutions of Pell’s equations could both be seen as arising from degenerate cases of the usual group structure on elliptic curves.
If it’s true, one could write a nice Whiggish history of Diophantine equations organized around the theme of ‘group laws’. I certainly would have understood number theory a bit better if someone had told me that tale.
If you can dig up anything on group structures on degenerate cubics, I’d be very interested. I’ll try to learn a bit about the history of the stereographic projection trick.
One can’t help wonder what’s in the lost works of Diophantus. (Right now I’m having a huge amount of fun reading The Archimedes Codex by Reviel Netz and William Noel, so my interest in the lost history of Greek mathematics is re-energized.)
Neither am I, which is why I put ‘real form’ in quotes. I know about real forms of complex Lie or associative algebras or (a bit more to the point) complex algebraic varieties, but clearly that idea generalizes a lot…
Great, that’s what I figured. I suppose to be more conservative in this Diophantine context one might tensor with an imaginary quadratic extension of rather than
rather than  . For example, if you look for solutions of
. For example, if you look for solutions of 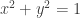 in
in  you’ll find Pythagorean triples. But if you adjoin
you’ll find Pythagorean triples. But if you adjoin  and then look for solutions of this equation, you’ll also find rational solutions of
and then look for solutions of this equation, you’ll also find rational solutions of  .
.
[…] Another interesting impression of the mathematical capabilities is possible from a tablet showing a representation of the square root of 2. It has been discussed by Richard Elwes in his blog post Babylon and the Square Root of 2. […]
So one of the oldest records of square roots in history would be The Old Babylonian tablet YBC 7289, which dates back anywhere from 2000-1600 BC. It depicts a square with two diagonals drawn and on the diagonals are numbers; when they are calculated, you get a very close approximation of the square root of 2 for the diagonal. Their value for the square root of two was about 1.41421297; I could have my students quickly calculate the square root of two (about 1.41421356) and mention to my students that this is pretty impressive for a civilization without modern day technology. The fact that they used clay tablets for math calculations shows how little they had to work with. Yet Babylon was also one of the most famous ancient cities in Mesopotamia; it’s mentioned multiple times in the bible and they were pretty advanced in mathematics for their area, despite the lack of resources we have today. They used a sexagesimal number system, which is base 60; they could solve algebra problems and work with what we now call Pythagorean triples; they could also solve equations with cubes.
As for the questions concerning group laws, I have written about this a couple of years ago (https://arxiv.org/abs/math/0311306). The stereographic projection is related to the group structure on the tangent of the circle. And Isabelle Dechene has written a thesis about generalized Jacobians where the degenerate aspect is taken care of (http://www.math.mcgill.ca/darmon/theses/dechene/thesis.pdf).
Thanks!
Thanks! That looks very interesting, and it is unexpectedly relevant (or at least adjacent) to one of my research problems.
Recently another Babylonian mathematical clay tablet has been in the news. The tablet, Plimpton 322, is very interesting. Unfortunately the news is mostly hype and misinformation. My analysis:
• Babylon? Babble On!, 30 August 2017.
[…] https://johncarlosbaez.wordpress.com/2011/12/02/babylon-and-the-square-root-of-2/ […]
[…] Babylon and the Square Root of 2 […]
[…] But I said "Western world" before. In fact, a form of the method of successive approximations was known to the Babylonians for finding the square root of a positive number, which is very similar to applying Newton's method to the quadratic equation x2−a=0. There's a nice blog post by John Baez and Richard Elwes about that. […]
[…] We see a lot of papers and talk about ancient Babylonians exactness of calculating the value of square root of 2. For example: https://johncarlosbaez.wordpress.com/2011/12/02/babylon-and-the-square-root-of-2/ […]