Ever since I was a kid, I’ve loved Archimedean tilings of the plane: that is, tilings by regular polygons where all the edge lengths are the same and every vertex looks alike. Here’s my favorite:
There are also 11 others, two of which are mirror images of each other. But how do we know this? How do we list them all and be sure we haven’t left any out?
The interior angle of a regular -sided polygon is obviously
since it’s a bit less than 180 degrees, or and how much?— well,
times a full turn, or
But these
‘s are getting annoying: it’s easier to say ‘a full turn’ than write
Then we can say the interior angle is
times a full turn.
Now suppose we have an Archimedean tiling where polygons meet: one with
sides, one with
sides, and so on up to one with
sides. Their interior angles must add up to a full turn. So, we have
or
or
So: to get an Archimedean tiling you need n whole numbers whose reciprocals add up to one less than n/2.
Looking for numbers like this is a weird little math puzzle. The Egyptians liked writing numbers as sums of reciprocals, so they might have enjoyed this game if they’d known it. The tiling I showed you comes from this solution:
since it has 3 polygons meeting at each vertex: a 4-sided one, a 6-sided one and a 12-sided one.
Here’s another solution:
It gives us this tiling:
Hmm, now I think this one is my favorite, because my eye sees it as a bunch of linked 12-sided polygons, sort of like chain mail. Different tilings make my eyes move over them in different ways, and this one has a very pleasant effect.
Here’s another solution:
This gives two Archimedean tilings that are mirror images of each other!
Of course, whether you count these as two different Archimedean tilings or just one depends on what rules you choose. And by the way, people usually don’t say a tiling is Archimedean if all the polygons are the same, like this:
They instead say it’s regular. If modern mathematicians were inventing this subject, we’d say regular tilings are a special case of Archimedean tilings—but this math is all very old, and back then mathematicians treated special cases as not included in the general case. For example, the Greeks didn’t even consider the number 1 to be a number!
So here’s a fun puzzle: classify the Archimedean tilings! For starters, you need to find all ways to get whole numbers whose reciprocals add up to one less than
. That sounds hard, but luckily it’s obvious that
since an equilateral triangle has the smallest interior angle, of any regular polygon, and you can only fit 6 of them around a vertex. If you think a bit, you’ll see this cuts the puzzle down to a finite search.
But you have to be careful, since there are some solutions that don’t give Archimedean tilings. As usual, the number 5 causes problems. We have
but there’s no way to tile the plane so that 2 regular pentagons and 1 regular decagon meet at each vertex! Kepler seems to have tried; here’s a picture from his book Harmonices Mundi:
It works beautifully at one vertex, but not for a tiling of the whole plane. To save the day he had to add some stars, and some of the decagons overlap! The Islamic tiling artists, and later Penrose, went further in this direction.
If you get stuck on this puzzle, you can find the answer here:
• Michal Krížek, Jakub Šolc, and Alena Šolcová, Is there a crystal lattice possessing five-fold symmetry?, AMS Notices 59 (January 2012), 22-30.
• Combinations of regular polygons that can meet at a vertex, Wikipedia.
Not enough?
In short, all Archimedean tilings of the plane arise from finding whole numbers whose reciprocals sum to
But what if the total is not enough? Don’t feel bad: you might still get a tiling of the hyperbolic plane. For example,
so you can’t tile the plane with 3 heptagons meeting at each corner… but you still get this tiling of the hyperbolic plane:
which happens to be related to a wonderful thing called Klein’s quartic curve.
You don’t always win… but sometimes you do, so the game is worth playing. For example,
so you have a chance at a tiling of the hyperbolic plane where five equilateral triangles and a square meet at each vertex. And in this case, you luck out:
For more beautiful pictures like these, see:
• Uniform tilings in hyperbolic plane, Wikipedia.
• Don Hatch, Hyperbolic tesselations.
Too much?
Similarly, if you’ve got reciprocals that add up to more than
, you’ve got a chance at tiling the sphere. For example,
and in this case we luck out and get the snub dodecahedron. I thought it was rude to snub a dodecahedron, but apparently not:
These tilings of the sphere are technically called Archimedean solids and (if all the polygons are the same) Platonic solids. Of these, only the snub dodecahedron and the ‘snub cube’ are different from their mirror images.
Fancier stuff
In short, adding up reciprocals of whole numbers is related to Archimedean tilings of the plane, the sphere and the hyperbolic plane. But this is also how Egyptians would write fractions! In fact they even demanded that all the reciprocals be distinct, so instead of writing 2/3 as , they’d write
It’s a lousy system—doubtless this is why King Tut died so young. But forget about the restriction that the reciprocals be distinct: that’s silly. If you can show that for every the number
can be written as
for whole numbers
you’ll be famous! So far people have ‘only’ shown it’s true for
up to a hundred trillion:
• Erdös–Straus conjecture, Wikipedia.
So, see if you can do better! But if you’re into fancy math, a less stressful activity might be to read about Egyptian fractions, tilings and ADE classifications:
• John Baez, This Week’s Finds in Mathematical Physics (Week 182).
This only gets into ‘Platonic’ or ‘regular’ tilings, not the more general ‘Archimedean’ or ‘semiregular’ ones I’m talking about today—so the arithmetic works a bit differently.
For the special magic arising from
see:
• John Baez, 42.
In another direction, my colleague Julie Bergner has talked about how they Egyptian fractions show up in the study of ‘groupoid cardinality’:
• Julie Bergner, Groupoids and Egyptian fractions.
So, while nobody uses Egyptian fractions much anymore, they have a kind of eerie afterlife. For more on what the Egyptians actually did, try these:
• Ron Knott, Egyptian fractions.
• Egyptian fractions, Wikipedia.










Thanks for the colorful pix and even an animation.
Along these lines, one of my current favorite Archimedean solids is the truncated icosidodecahedron, which looks sort of like your first favorite at the top of the article. It’s got a pleasing mix of shapes and sizes, and it’s the Cayley graph of the Coxeter group (which is in turn the full group of isometries of the icosahedron).
(which is in turn the full group of isometries of the icosahedron).
It’s also called “the great rhombicosidodecahedron”. Don’t you love these quaint old-fashioned names? :-)
I too love the great rhombicosidodecahedron! It’s great! Since I’m the only one who can include images in the comments here, it’s my duty to show everyone what we’re talking about:
As you hinted, it’s what we get when we replace the hexagons in the great rhombitrihexagonal tiling by pentagons:
So, here’s a question for you, Todd: is this tiling also the Cayley graph of some group? Maybe a group coming from an affine Coxeter diagram?
Yes, I think the name of a polytope should resemble its appearance, so if it has lots of faces of different shapes its name needs lots of shiny, sophisticated syllables.
The modern standard name for the ‘great rhombitrihexagonal tiling’ is apparently the ‘truncated trihexagonal tiling’. Conway has his own names for all these, and for him it’s the ‘truncated hexadeltille’. I like the idea of extended Schläfli symbols, which seek to reduce this fancy nomenclature to a logical numerical code, but even these seem to stagger under the sheer diversity of interesting polytopes. Hmm, Wikipedia says these gave way to Coxeter diagrams. That suggests I could look up the answer to my question to you—but I won’t!
My off-hand guess is yes, it’s the Cayley graph of the Coxeter group whose Coxeter matrix is 3 by 3 and whose off-diagonal entries are
is 3 by 3 and whose off-diagonal entries are 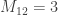 ,
,  , and
, and 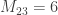 . However, I’m drinking right now (it’s the Superbowl), and last time I drank and posted I said some things which were embarrassingly wrong. I should come back to this later, when I can look into this more closely.
. However, I’m drinking right now (it’s the Superbowl), and last time I drank and posted I said some things which were embarrassingly wrong. I should come back to this later, when I can look into this more closely.
It sounds like you’re guessing what I’d guess: you’re taking the Coxeter diagram here:
here:
and jacking up the 5 by one to get this:
6 o---o---oIf that’s right, I feel like calling the result an ‘affine Coxeter diagram’, but I don’t think I’ve actually ever seen it. Hmm… oh yes, it’s called in this list on Wikipedia. They even discuss how these diagrams are related to ‘uniform tilings’ of the plane, which I’ve been calling Archimedean tilings.
in this list on Wikipedia. They even discuss how these diagrams are related to ‘uniform tilings’ of the plane, which I’ve been calling Archimedean tilings.
Just found out that a ‘snub’ — also called an alternation — is a certain process for deriving polytopes. It’s also called ‘snubification’. :-)
I think that you have a typo in the formula where you introduce Kepler’s attempted tiling (5, 5, 10).
You’re right! I’ll fix it now. Thanks!
Great going John, Bravo!
I’m not a scientist, but I love new angles on things – gravity as an entropic by-product, amazing!
Since hyperbolic space has an intrinsic length scale, if you make polygons very small, they begin to behave more like Euclidean ones.
If you made the heptagons in the (7,3) tiling of the hyperbolic plane a little larger, they wouldn’t quite reach all the way around, and would begin to leave a gap rather like pentagons do in Euclidean space. Is there a regular hyperbolic polyhedron whose sides are all heptagons?
I have no idea what you mean by a “regular hyperbolic polyhedron”!
If you hadn’t said more, I’d assume you meant a tiling of the hyperbolic plane by regular polygons—just as an ordinary regular polyhedron is a tiling of the 2-sphere by regular polygons. Spherical geometry and hyperbolic geometry are the two most symmetrical non-Euclidean 2d geometries.
And so, if someone asked me about a “regular hyperbolic polyedron whose sides are all heptagons”, I’d show them this:
But, given the rest of what you said, I’d guess you’re thinking about a tiling of the “hyperbolic 2-sphere” by regular heptagons. The problem is, there’s no such thing as the “hyperbolic 2-sphere”: thanks to the Gauss–Bonnet theorem, there’s no way to give the 2-sphere a Riemannian metric with everywhere negative curvature.
Take a n-holed torus, give it a Riemannian metric, and tile it with heptagons whose sides are geodesics and whose interior angles are the usual interior angles of a regular heptagon. Then n can’t be 0 or 1; it must be 2 or more. Again this is a spinoff of the Gauss–Bonnet theorem.
Luckily, you can give the 3-holed torus a metric with constant negative curvature, and tile it by 24 heptagons whose sides geodesics and whose interior angles are the usual interior angles of a regular heptagon. This gadget is the closest thing I have to a good answer to your question. This is called ‘Klein’s quartic curve’ and I have a nice webpage on it.
It’s hard to visualize this 3-holed torus because you can’t embed it in Euclidean 3d space in a metric-preserving way. But that webpage has lots of pictures. In particular, you can get Klein’s quartic curve by taking the hyperbolic plane and ‘curling it up’, identifying heptagons that have the same numbers here:
This in fact gives the most symmetrical Riemannian metric possible on a 3-holed torus! The symmetry group of the 3-holed torus with this metric has 336 elements. That number is 24 × 7 × 2. You’ve seen the numbers 24 and 7 in my discussion already; the factor of 2 comes from an orientation-reversing symmetry.
(Coincidentally, 336 is the number of hours in a fortnight).
The hyperbolic plane has a constant negative Gaussian curvature K. Define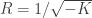 ; this is a length scale intrinsic to the space. A regular heptagon will have the sum of its exterior angles be greater than 360 degrees, but how much greater depends on the size of the heptagon. Only when the heptagon is the correct size will the exterior angle be 60 degrees so we can fit three of them together at a vertex to get the (7,3) tiling. If they’re large enough, the external angle becomes 90 degrees and we get the (7,4) tiling.
; this is a length scale intrinsic to the space. A regular heptagon will have the sum of its exterior angles be greater than 360 degrees, but how much greater depends on the size of the heptagon. Only when the heptagon is the correct size will the exterior angle be 60 degrees so we can fit three of them together at a vertex to get the (7,3) tiling. If they’re large enough, the external angle becomes 90 degrees and we get the (7,4) tiling.
Between these two sizes, seven heptagons around a central one leave a gap, rather like five pentagons around a central one. In Euclidean 3-space we can curl up pentagons into a dodecahedron; we can do the same in hyperbolic 3-space for pentagons of the correct size whose external angles are 90 degrees—in fact, these tile hyperbolic 3-space and one appears in the Mathematica logo. Since these “hyperbolic dodecahedra” exist, I was wondering if one can use the gap between heptagons in the hyperbolic plane whose size is somewhere between the ones in the (7,3) and (7,4) tiling of the plane to curl them up into a polyhedron with regular heptagons as sides.
I guess I might as well start with hexagons rather than heptagons. Is it possible to have a hyperbolic polyhedron with three hexagons meeting at a vertex? The hyperbolic dodecahedron has dihedral angles of 90 degrees and tiles hyperbolic 3-space; every vertex has three orthogonal lines passing through it, and there are planar slices that result in the (5,4) tiling of the hyperbolic plane. What prevents a similar construction involving hexagons and the (6,4) plane?
I still don’t really understand what you’re saying, so I’ll just blather at random.
I’m pretty sure it’s impossible to take a sphere and subdivide its surface into just hexagons, or indeed any mix of just hexagons, heptagons, octagons, nonagons and so on. You need some polygons with fewer sides! This should be a purely topological result, nothing to do with the geometry of the sphere or the polygons: their edges don’t need to be ‘straight’ in any sense. It should follow from Euler’s formula
where is the genus, or number of holes in our doughnut; here
is the genus, or number of holes in our doughnut; here 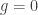 .
.
It’s easiest for me to explain this in the case where we imagine subdividing a sphere into heptagons with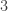 meeting at each vertex. You can easily generalize what I’m about to say.
meeting at each vertex. You can easily generalize what I’m about to say.
In this special case we have
since each face has 7 edges but each edge is shared by 2 faces. We also have
since each vertex has 3 edges coming out of it, but each edge ends at 2 vertices.
So
and thus
so the problem is, there’s no way to obtain
with a positive number of faces. (Please don’t invent polyhedra with a negative number of faces to get around this, at least not today.)
So, we can’t ’tile’ a 2-sphere, no matter how irregularly, with heptagons meeting three at a vertex. Nor can we do a torus, since that would require . If we try a 2-holed torus we get
. If we try a 2-holed torus we get
so maybe we can do that with 12 heptagons—I don’t know. The case I’m most familiar with is the 3-holed torus, which gives
or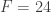 . That’s why we can tile a 3-holed torus with 24 heptagons meeting 3 at each vertex! Or dually we can tile the 3-holed torus with triangles, 7 meeting at each of 24 vertices, as shown in this picture by Greg Egan:
. That’s why we can tile a 3-holed torus with 24 heptagons meeting 3 at each vertex! Or dually we can tile the 3-holed torus with triangles, 7 meeting at each of 24 vertices, as shown in this picture by Greg Egan:
If you allow more than 3 heptagons to meet at some vertices we instead have
and I think you can show it’s still impossible to tile a sphere, which would require
I get the impression you’re trying to violate such laws of topology.
That’s a great proof, thank you!
Thanks!
I noticed yesterday that we can easily tile a sphere with just two heptagons: take one to be the northern hemisphere, one to be the southern hemisphere, and divide the equator into 7 segments.
But in this case we only have two heptagons meeting at each vertex: that’s a bit degenerate.
So let me show that you can’t subdivide a sphere into just polygons with 6 or more sides, if at least 3 polygons meet at each vertex. By the reasoning above, if we could do this we’d have
So, expressing everything in terms of edges, we get
so
so
which contradicts
This argument also gives a bit more. For a torus we must have
There are lots of ways to subdivide a torus into hexagons that meet 3 at a vertex: just take a hexagonal lattice and curl it up. But if we try to stick in one or more polygons with more than 6 edges, or try to have more than 3 hexagons meet somewhere, the argument above shows we’re doomed: then we’ve tipped the situation over from
to
A similar calculation shows that if you subdivide a sphere into just hexagons and pentagons, with 3 meeting at each vertex, there have to be exactly 12 pentagons. People working on fullerenes know this well! The first interesting example is this:
but people go further, like this:
I read this blog quite often and have never had much to share but I think my friends post that I read moments before this fits this blog quite nicely…It may not be “Great”, but behold, the recycled rhombicosidodecahedron!
Nice, Forrest Sheldon! Here’s one photo from that blog post… but people here should read the whole thing:
Awesome! These past few weeks I’ve had a craving for a bunch of Magnetix, precisely to construct such a thing… but you can’t buy them in stores anymore because of a recall a few years back.
[…] John Baez: Archimedean Tilings and Egyptian Fractions […]
[…] Hyperbolic geometry is fun. And it’s much easier to create regular & semi-regular tessellations in the hyperbolic plane than in the Euclidean plane. John Baez discussed this topic a little while ago: Archimedean Tilings and Egyptian Fractions […]
It turns out that if you look for natural numbers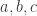 that make
that make
as close to 1 as possible, while still less than 1, the very best you can do is It comes within
It comes within 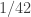 of equalling 1, and this has amazing consequences.
of equalling 1, and this has amazing consequences.
Archimedean hyperbolic tilings get much more interesting with 4 or more edges per vertex. At this point, there is a possibility of having several different tilings which, nonetheless, have the same sequence of polygons around a vertex.
For example, a tiling with three hexagons and one triangle around each vertex has three different forms. With more complex vertex configurations, there can be many distinct tilings.
Is there a place I can see pictures of these?
Well, basics of the theory is here:
http://bendwavy.org/klitzing/explain/tiling-conf.htm
Some pictures are at http://superliminal.com/geometry/tyler/gallery/hyperbolic/6664-all.html, http://superliminal.com/geometry/tyler/gallery/hyperbolic/666p.html and http://superliminal.com/geometry/tyler/gallery/hyperbolic/marek3.html
Lately, I tried using HyperbolicApplet (http://aleph0.clarku.edu/~djoyce/poincare/PoincareApplet.html), but it requires some image editing to get a proper colored picture.
[…] in classifying tilings of the regular surfaces (the plane, sphere, and hyperbolic plane); see e.g. https://johncarlosbaez.wordpress.com/2012/02/05/archimedean-tilings-and-egyptian-fractions/ for a nice discussion of […]