At last—a textbook on category theory for scientists! And it’s free!
• David Spivak, Category Theory for Scientists.
It’s based on a course the author taught:
This course is an attempt to extol the virtues of a new branch of mathematics, called category theory, which was invented for powerful communication of ideas between different fields and subfields within mathematics. By powerful communication of ideas I actually mean something precise. Different branches of mathematics can be formalized into categories. These categories can then be connected together by functors. And the sense in which these functors provide powerful communication of ideas is that facts and theorems proven in one category can be transferred through a connecting functor to yield proofs of an analogous theorem in another category. A functor is like a conductor of mathematical truth.
I believe that the language and toolset of category theory can be useful throughout science. We build scientific understanding by developing models, and category theory is the study of basic conceptual building blocks and how they cleanly fit together to make such models. Certain structures and conceptual frameworks show up again and again in our understanding of reality. No one would dispute that vector spaces are ubiquitous. But so are hierarchies, symmetries, actions of agents on objects, data models, global behavior emerging as the aggregate of local behavior, self-similarity, and the effect of methodological context.
Some ideas are so common that our use of them goes virtually undetected, such as set-theoretic intersections. For example, when we speak of a material that is both lightweight and ductile, we are intersecting two sets. But what is the use of even mentioning this set-theoretic fact? The answer is that when we formalize our ideas, our understanding is almost always clarified. Our ability to communicate with others is enhanced, and the possibility for developing new insights expands. And if we are ever to get to the point that we can input our ideas into computers, we will need to be able to formalize these ideas first.
It is my hope that this course will offer scientists a new vocabulary in which to think and communicate, and a new pipeline to the vast array of theorems that exist and are considered immensely powerful within mathematics. These theorems have not made their way out into the world of science, but they are directly applicable there. Hierarchies are partial orders, symmetries are group elements, data models are categories, agent actions are monoid actions, local-to-global principles are sheaves, self-similarity is modeled by operads, context can be modeled by monads.
He asks readers from different subjects for help in finding new ways to apply category theory to those subjects. And that’s the right attitude to take when reading this book. I’ve found categories immensely valuable in my work. But it took effort to learn category theory and see how it can apply to different subjects. People are just starting to figure out these things, so don’t expect instant solutions to the problems in your own favorite field.
But Spivak does the best job I’ve seen so far at explaining category theory as a general-purpose tool for thinking clearly. Since I’m busy using category theory to clarify the relationships between fields like chemistry, population biology, electrical engineering and control theory, this subject is very much on my mind.
Azimuth 
Cool, thanks! I always thought it would be fun to try and write a book on category theory for kindergarten kids. If they can draw a venn diagram, then surely they can draw a pushout diagram? (okay, maybe elementary school, rather than kindergarten, but still…)
We’ll get it down to kindergarten eventually! First, college.
My personal effort to teach category theory to people without advanced mathematical experience mostly fails somewhere near the Yoneda lemma, because it’s near the complexity limit where a non-trivial elementary example can be written on a single (“tiny”) piece of paper.
Kan extensions and bicategories have been clearly beyond. Even limits and colimits outside Set seem to be hard to construct in a generic way for most people. The obstacle mostly is my missing capability to connect the notions with their everyday’s experience.
Not quite too serious: Did you ever think about a continuum hypotheses for aleph-n-categories?
I have never thought about
-categories for 
beyond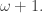 
Here’s an interesting exposition ( http://bartoszmilewski.com/category/category-theory/ ) by Bartosz Milewski that introduces category theory and goes on to derive Yoneda’s lemma using numerous examples to illustrate important concepts employed. Most of the examples involve simple Haskell programs and the diagrams include piggies, sacks of potatoes and fireworks (I kid you not!), presumably inspired by the lessons the author used to teach his 10-year old son about categories. As to practical applications of category theory, it is claimed that anyone who wants to understand implementations of Haskell or be involved in its extensions must have a basic understanding of category theory. Amazing!
Thanks for the link! You can’t use Haskell without using monads. More generally, there’s a kind of computer scientist who uses lots of ideas from category theory, and that’s one reason I like talking to computer scientists.
I hope Bartosz Milewski explains the Yoneda Lemma in ways that make it accessible to more people. It’s very simple in a way, and very important, but it seems to require a lot of work for most people to understand it and (harder) appreciate its applications. That was certainly true for me. I have a couple of students now who need this lemma in their work on network theory, so I’ve been seeing how quickly and easily I can get them to understand it. I have certain pedagogical tricks that seem to work….
Here’s a better link:
It goes directly to the Understanding Yoneda tutorial. He has a posting on monads too.
I thought “Conceptual Mathematics: A First Introduction to Categories” was the kindergarten version.
I like Steve’s idea. I have been considering a compromise to these two extremes: use elementary category theory as a teaching tool to help explain the mathematics required by theoretical physics. For example, an understanding of gauge theory requires knowledge of group theory, Lie groups, vector spaces, topology, differential geometry (including bundles, connections, lifts, etc.), differential forms, and of course good old calculus. I have been following this path for the past couple of years and based on a lot of experience have developed a couple of strong convictions. 1) There are some basic ideas that come up over and over in these various “unrelated” mathematical fields that should be taught to everyone who wants to apply advanced math to solving physical problems. For example, morphisms show up all over the place. If someone had taken me aside and shown me the most basic category theory and how to apply it, the appreciation of all these morphisms would have come so much sooner and easier! And consequently, the understanding of the various mathematical topics would have come much more quickly. 2) The second thing that I have learned is that, for me, having a physical problem to be solved while learning all this abstract math makes it much, much easier to keep focused and to achieve a natural, intuitive understand of the underlying math required to solve the physical problem. Some of the better books do this (for example, “Gauge fields, Knots and Gravity” to which I am deeply indebted), but the mission of these books is to focus more heavily on the mathematics and less so on the physical problem to be solved. Alternatively, a presentation focused on the most basic mathematical framework required, motivated each step of the way, as each new mathematical tool is introduced, by an explanation of why it is needed to ultimately solve the problem, could be structured in a way that an interested high school student could understand. And elementary category theory (what better way to learn that maps are everything?!) would be the perfect place to start. So yes, category theory is going to change the way the pros think about their areas of specialty and do mathematical research. But I think the time has also come to start using elementary category theory as a teaching tool, together with simple, concrete examples, to making abstract mathematical concepts seem more natural and easier to understand. But I’m just an amateur. What think ye?
I think it’s great to try using category theory to explain other things. One has to experiment to see what works.
Right now I’m deeply immersed in a somewhat different quest, namely to understand the category theory that secretly underlies lots of applied math and engineering—for example, electric circuit theory and control theory. Someday that stuff might be explained using a little category theory! But if so, clearly we need to start by understanding that stuff using category theory.
It’s mainly the more ‘pure’ areas of math where the experts already understand them using category theory and all we need to do is pass that understanding on.
There’s a lovely classic from 1985 by Robert Geroch, Mathematical Physics. No physics inside actually, except Minkowski space. He uses elementary category language to teach multilinear algebra, topological spaces, spectral theorem, etc. Alas no Yoneda, and no metrization of uniform spaces.
In “Modern Differential Geometry for Physicists”, Second Edition, p79, Chris J. Isham comments that category theory is the natural language to describe many of the constructions made in differential geometry, but then goes on to say he will not introduce such ideas formally in the book. He suggests that a good introduction to a category-based view of differential geometry is given in Lang, S. (1972), Differential manifolds, Addison Wesley, London. I haven’t had the opportunity to check Lang. Is anyone here familiar with that book, and do you have an opinion as to how effective the use of category theory is as an expository technique in this book? That is, is the book more effective as a result of using category theory than it would be without using it? Do you feel that the additional learning overhead imposed in order to become proficient with the necessary category theory is compensated for by subsequent benefits in comprehension and leaning speed?
Charlie wrote:
Interesting! That’s a great book, but I hadn’t remembered that remark.
When I first met Isham, he was famous for being a very well-informed critic of all known approaches to quantum gravity. He thought none of these approaches were sufficiently radical. Later, he went on to develop an approach to quantum physics based on category theory—or more specifically, the branch of category theory called topos theory, which takes the category of sets and functions and generalizes it to ‘topoi’, which are categories in which you can do all of mathematics, just as you can do all mathematics with sets and functions. Here’s a nontechnical intro to this line of thought:
• Chris Isham, Topos methods in the foundations of physics.
I’m not familiar with that book, though I’m familiar with Lang: when I was a postdoc, he was often the only other guy in the math department at 2 am. He wrote a book a year, apparently while he took a summer cruise across the Atlantic. I learned complex analysis as an undergrad from his book Complex Analysis, and I liked that book a lot.
Charlie Clingen wrote eventually:
I’ve read that book and like it. I already knew category theory and differential topology, so it’s hard to say how well it did at explaining those to beginners. As I recall, the category theory was gentle, but the differential topology was advanced, with infinite-dimensional manifolds almost from the start.
Thanks, Toby. I was able to do a quick scan on Amazon of S. Lang’s Introduction to Differentiable Manifolds (2002), which seems to be an update of his earlier text and apparently limited to finite-dimensional manifolds. There is a 4-page introduction to category theory at the front of the book, and frequent references to category concepts in the body of the book. But I agree with your assessment – the book is definitely too advanced for beginners. However it does seem to offer an opportunity to assess the value of what category theory brings to the description of a mathematical topic. My question to you, Toby, or to someone with your background, would be, to what extent (whatever that means) does the use of category theory in this book aid in the presentation and explanation of the concepts of differentiable manifolds? Or put differently, if all the category theory terminology were removed, would the book become significantly less useful? I realize this is pretty vague, but at least it is a fairly narrowly-defined problem that might give some specific insight into the value of using category theory as a tool to describe and teach mathematical concepts.
The category theory was helpful, but largely because (already being familiar with category theory) I already wanted to know more about the category of differentiable manifolds qua a category. (In particular, I really needed to know about it qua a site for my doctoral research, and reading Lang helped orient my thoughts properly even where it didn’t directly give me the answers that I needed.) To say more, I would really have to look at the book again. (I might have a copy downstairs.)
Since category theory is about making connections, it might be worth discussing how category theory as outlined by David could be related to the semantic web. Also specifically how it may be reused in terms of a predicate logic foundation for an ontology-based knowledgebase. Or something like that.
In any case, it sounds very intriguing.
Jocelyn Paine also has general ideas on bringing category theory into scientific thinking. He wrote a little on this here at the n-Category Cafe. He also has some web-based interactive demonstrations that illustrate basic categorical constructions, here.
A small example from my own experience is when I wanted to get my head around some of the basic theory of irreducible continuous unitary representations of the Poincaré group, which is important in quantum physics. We had a long, long discussion of it at the Café. This topic is of course old and treated in loads of places, but for some reason I just wasn’t grokking it, until at last I pictured a groupoid whose objects are 4-momenta (on a hyperbolic sheet of given mass
). At a given object 
, the hom 
would be a “little group” of Poincaré group elements that fix 
. This picture served as a useful intermediary; in the end one can consider a groupoid whose objects are pairs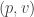 
where 
is an element of an irrep of a typical such little group. This groupoid is another way of packaging the data of a unitary irrep of the Poincaré group.
In summary, thinking in terms of groupoids gave me a graphical picture that recapitulated the standard little group analysis in a concrete visual way. That was very helpful. And I think that’s a large part of the appeal and power of category theory: it enables one to visualize abstract fundamental mathematical properties in terms of graphical pictures and patterns, where they become easier to mentally hold, so to speak.
[…] Reading: John Carlos Baez website, May […]
As I understand category theory can be used to make connections between different areas of science and to possibly understand theories at a more fundamental level. However, is there any practical advantage to formulating a theory using categories? Specifically, does category theory provide new insights or ideas to already developed scientific theories? I am wondering for example if formulating inverse problem theory using categories leads to any advantages.
I don’t know what “inverse problem theory” is, so I can’t help you with that example. In physics the power of category theory is by now well-established: a bunch of physical systems are described by ‘modular tensor categories’, and this way of thinking about them is crucial for understanding things like the quantum Hall effect, anyons, etc. I also believe that quantum theory and gravity can only be unified by seeing their relationship with the help of categories. Category theory is also widely recognized to be important in computer science, e.g. the use of monads in Haskell, the relation of the lambda-calculus to cartesian closed categories, and the like.
In other branches of science categories have not yet proved their worth, but I’m personally convinced that this is mainly because nobody has put a sustained effort into applying them there. That’s what I’m working on now.
[…] As Artem helpfully suggests in a comment to the question, you might want to try David Spivak’s Category Theory for Scientists (Old Version). See also the MIT OpenCourseware page and John Baez’s blog entry. […]