
The physicists Dirac and Feynman, both bold when it came to new mathematical ideas, both said we should think about negative probabilities.
These days, Kolmogorov’s axioms for probabilities are used to justify formulating probability theory in terms of measure theory. Mathematically, the theory of measures that take negative or even complex values is well-developed. So, to the extent that probability theory is just measure theory, you can say a lot is known about negative probabilities.
But probability theory is not just measure theory; it adds its own distinctive ideas. To get these into the picture, we really need to ask some basic questions, like: what could it mean to say something had a negative chance of happening?
I really have no idea.
In this paper:
• Paul Dirac, The physical interpretation of quantum mechanics, Proc. Roy. Soc. London A 180 (1942), 1–39.
Dirac wrote:
Negative energies and probabilities should not be considered as nonsense. They are well-defined concepts mathematically, like a negative of money.
In fact, I think negative money could have been the origin of negative numbers. Venetian bankers started writing numbers in red to symbolize debts—hence the phrase ‘in the red’ for being in debt. So, you could say negative numbers were invented to formalize the idea of debt and make accounting easier. Bankers couldn’t really get rich if negative money didn’t exist.
A negative dollar is a dollar you owe someone. But how can you owe someone a probability? I haven’t figured this out.
Unsurprisingly, the clearest writing about negative probabilities that I’ve found is by Feynman:
• Richard P. Feynman, Negative probability, in Quantum Implications: Essays in Honour of David Bohm, eds. F. David Peat and Basil Hiley, Routledge & Kegan Paul Ltd, London, 1987, pp. 235–248.
He emphasizes that even if the final answer of a calculation must be positive, negative numbers are often allowed to appear in intermediate steps… and that this can happen with probabilities.
Let me quote some:
Some twenty years ago one problem we theoretical physicists had was that if we combined the principles of quantum mechanics and those of relativity plus certain tacit assumptions, we seemed only able to produce theories (the quantum field theories) which gave infinity for the answer to certain questions. These infinities are kept in abeyance (and now possibly eliminated altogether) by the awkward process of renormalization. In an attempt to understand all this better, and perhaps to make a theory which would give only finite answers from the start, I looked into the” tacit assumptions” to see if they could be altered.
One of the assumptions was that the probability for an event must always be a positive number. Trying to think of negative probabilities gave me cultural shock at first, but when I finally got easy with the concept I wrote myself a note so I wouldn’t forget my thoughts. I think that Prof. Bohm has just the combination of imagination and boldness to find them interesting and amusing. I am delighted to have this opportunity to publish them in such an appropriate place. I have taken the opportunity to add some further, more recent, thoughts about applications to two state systems.
Unfortunately I never did find out how to use the freedom of allowing probabilities to be negative to solve the original problem of infinities in quantum field theory!
It is usual to suppose that, since the probabilities of events must be positive, a theory which gives negative numbers for such quantities must be absurd. I should show here how negative probabilities might be interpreted. A negative number, say of apples, seems like an absurdity. A man starting a day with five apples who gives away ten and is given eight during the day has three left. I can calculate this in two steps: 5 -10 = -5 and -5 + 8 + 3. The final answer is satisfactorily positive and correct although in the intermediate steps of calculation negative numbers appear. In the real situation there must be special limitations of the time in which the various apples are received and given since he never really has a negative number, yet the use of negative numbers as an abstract calculation permits us freedom to do our mathematical calculations in any order simplifying the analysis enormously, and permitting us to disregard inessential details. The idea of negative numbers is an exceedingly fruitful mathematical invention. Today a person who balks at making a calculation in this way is considered backward or ignorant, or to have some kind of a mental block. It is the purpose of this paper to point out that we have a similar strong block against negative probabilities. By discussing a number of examples, I hope to show that they are entirely rational of course, and that their use simplifies calculation and thought in a number of applications in physics.
First let us consider a simple probability problem, and how we usually calculate things and then see what would happen if we allowed some of our normal probabilities in the calculations to be negative. Let us imagine a roulette wheel with, for simplicity, just three numbers: 1, 2, 3. Suppose however, the operator by control of a switch under the table can put the wheel into one of two conditions A, B in each of which the probability of 1, 2, 3 are different. If the wheel is in condition A, the probability of 1 is p1A = 0.3 say, of 2 is p2A = 0.6, of 3 is p3A =0.1. But if the wheel is in condition B, these probabilities are
p1B = 0.1, p2B = 0.4, p3B = 0.5say as in the table.
Cond. A Cond. B 1 0.3 0.1 2 0.6 0.4 3 0.1 0.5 We, of course, use the table in this way: suppose the operator puts the wheel into condition A 7/10 of the time and into B the other 3/10 of the time at random. (That is the probability of condition A, pA = 0.7, and of B, pB = 0.3.) Then the probability of getting 1 is
Prob. 1 = 0.7 (0.3) + 0.3 (0.1) = 0.24,etc.
[…]
Now, however, suppose that some of the conditional probabilities are negative, suppose the table reads so that, as we shall say, if the system is in condition B the probability of getting 1 is -0.4. This sounds absurd but we must say it this way if we wish that our way of thought and language be precisely the same whether the actual quantities pi α in our calculations are positive or negative. That is the essence of the mathematical use of negative numbers—to permit an efficiency in reasoning so that various cases can be considered together by the same line of reasoning, being assured that intermediary steps which are not readily interpreted (like -5 apples) will not lead to absurd results. Let us see what p1B = -0.4 “means” by seeing how we calculate with it.
He gives an example showing how meaningful end results can sometimes arise even if the conditional probabilities like p1B are negative or greater than 1.
It is not my intention here to contend that the final probability of a verifiable physical event can be negative. On the other hand, conditional probabilities and probabilities of imagined intermediary states may be negative in a calculation of probabilities of physical events or states. If a physical theory for calculating probabilities yields a negative probability for a given situation under certain assumed conditions, we need not conclude the theory is incorrect. Two other possibilities of interpretation exist. One is that the conditions (for example, initial conditions) may not be capable of being realized in the physical world. The other possibility is that the situation for which the probability appears to be negative is not one that can be verified directly. A combination of these two, limitation of verifiability and freedom in initial conditions, may also be a solution to the apparent difficulty.
The rest of this paper illustrates these points with a number of examples drawn from physics which are less artificial than our roulette wheel. Since the result must ultimately have a positive probability, the question may be asked, why not rearrange the calculation so that the probabilities are positive in all the intermediate states? The same question might be asked of an accountant who subtracts the total disbursements before adding the total receipts. He stands a chance of going through an intermediary negative sum. Why not rearrange the calculation? Why bother? There is nothing mathematically wrong with this method of calculating and it frees the mind to think clearly and simply in a situation otherwise quite complicated. An analysis in terms of various states or conditions may simplify a calculation at the expense of requiring negative probabilities for these states. It is not really much expense.
Our first physical example is one in which one· usually uses negative probabilities without noticing it. It is not a very profound example and is practically the same in content as our previous example. A particle diffusing in one dimension in a rod has a probability of being at
at time
of
satisfying
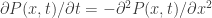
Suppose at
and
the rod has absorbers at both ends so that
there. Let the probability of being at
at
be given as
What is
thereafter? It is

where
is given by
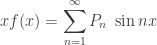
or

The easiest way of analyzing this (and the way used if
is a temperature, for example) is to say that there are certain distributions that behave in an especially simple way. If
starts as
it will remain that shape, simply decreasing with time, as
Any distribution
can be thought of as a superposition of such sine waves. But
cannot be
if
is a probability and probabilities must always be positive. Yet the analysis is so simple this way that no one has really objected for long.
He also gives examples from quantum mechanics, but the interesting thing about the examples above is that they’re purely classical—and the second one, at least, is something physicists are quite used to.
Sometimes it’s good to temporarily put aside making sense of ideas and just see if you can develop rules to consistently work with them. For example: the square root of -1. People had to get good at using it before they understood what it really was: a rotation by a quarter turn in the plane.
Along those, lines, here’s an interesting attempt to work with negative probabilities:
• Gábor J. Székely, Half of a coin: negative probabilities, Wilmott Magazine (July 2005), 66–68.
He uses rigorous mathematics to study something that sounds absurd: ‘half a coin’. Suppose you make a bet with an ordinary fair coin, where you get 1 dollar if it comes up heads and 0 dollars if it comes up tails. Next, suppose you want this bet to be the same as making two bets involving two separate ‘half coins’. Then you can do it if a half coin has infinitely many sides numbered 0,1,2,3, etc., and you win dollars when side number
comes up….
… and if the probability of side coming up obeys a special formula…
and if this probability can be negative sometimes!
This seems very bizarre, but the math is solid, even if the problem of interpreting it may drive you insane.
Let’s see how it works. Consider a game where the probability of winning
dollars is
Then we can summarize this game using a generating function:
Now suppose you play two independent games like this, and another one, say
with generating function
Then there’s a new game that consists of playing both games. The reason I’m writing it as
is that its generating function is the product
See why? With probability you win
dollars in game
and
dollars in game
for a total of
dollars.
The game where you flip a fair coin and win 1 dollar if it lands heads up and 0 dollars if lands tails up has generating function
The half-coin is an imaginary game such that playing two copies of this game is the same as playing the game
If such a game really existed, we would have
so
However, if you work out the Taylor series of this function, every even term is negative except for the zeroth term. So, this game can exist only if we allow negative probabilities.
(Experts on generating functions and combinatorics will enjoy how the coefficients of the Taylor series of involves the Catalan numbers.)
By the way, it’s worth remembering that for a long time mathematicians believed that negative numbers made no sense. As late as 1758 the British mathematician Francis Maseres claimed that negative numbers
… darken the very whole doctrines of the equations and make dark of the things which are in their nature excessively obvious and simple.
So opinions on these things can change. And since I’ve spent a lot of time working on ‘sets with fractional cardinality’, and have made lots of progress on that idea, and other strange ideas, I like to spend a little time now and then investigating other nonsensical-sounding generalizations of familiar concepts.
This paper by Mark Burgin has a nice collection of references on negative probability:
• Mark Burgin, Interpretations of negative probability.
He valiantly tries to provide a frequentist interpretation of negative probabilities. He needs ‘negative events’ to get negative frequencies of events occurring, and he gives this example:
To better understand how negative elementary events appear and how negative probability emerges, consider the following example. Let us consider the situation when an attentive person A with the high knowledge of English writes some text T. We may ask what the probability is for the word “texxt” or “wrod” to appear in his text T. Conventional probability theory gives 0 as the answer. However, we all know that there are usually misprints. So, due to such a misprint this word may appear but then it would be corrected. In terms of extended probability, a negative value (say, -0.1) of the probability for the word “texxt” to appear in his text T means that this word may appear due to a misprint but then it’ll be corrected and will not be present in the text T.
Maybe he’s saying that the misprint occurs with probability 0.1 and then it ‘de-occurs’ with the same probability, giving a total probability of
I’m not sure.
Here’s another paper on the subject:
• Espen Gaarder Haug, Why so negative to negative probabilities?, Wilmott Magazine.
It certainly gets points for a nice title! However, like Burgin’s paper, I find it a lot less clear than what Feynman wrote.
Notice that like Székely’s paper, Haug’s originally appeared in the Wilmott Magazine. I hadn’t heard of that, but it’s about finance. So it seems that the bankers, having invented negative numbers to get us into debt, are now struggling to invent negative probabilities! In fact Haug’s article tries some applications of negative probabilities to finance.
Scary.
For further discussion, with some nice remarks by the quantum physics experts Matt Leifer and Michael Nielsen, see the comments on my Google+ post on this topic. Matt Leifer casts cold water on the idea of using negative probabilities in quantum theory. On the other hand, Michael Nielsen points out some interesting features of the Wigner quasiprobability distribution, which is the best possible attempt to assign a probability density for a quantum particle to have any given position and momentum. It can be negative! But if you integrate it over all momenta, you get the probability density for the particle having any given position:
And if you integrate it over all positions, you get the probability density for the particle having any given momentum:

You’ll pardon me if I just squee like a young girl for a while. You’ve merged my avocation (nerding out about unifying mathematical tools across disciplines) with my vocation (mathematical modeling of markets.)
Please keep reading Wilmott. It’s a joy to see what you get out of it.
If probability less than zero can exist, then I’m 110% sure that probability above one can too.
I’m not so sure you’re right… I’m only 100% sure.
Joking aside, if then
then  where
where  , surely?
, surely?
Okay, my measure theory is very rusty, but let me think out loud a little here. If I recall correctly, from a measure theoretic standpoint, a real-valued measure on a measure space
on a measure space  is a probability measure assuming it is positive (i.e.,
is a probability measure assuming it is positive (i.e., 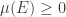 for all measurable sets
for all measurable sets  ) and
) and  . So, for negative probabilities, we’re really just relaxing the positivity condition on the measures we want to consider, right? Now, I have vague recollections of a theorem (associated with names like Hahn and Jordan, maybe?) that says you can decompose such a measure into a positive and negative part so that
. So, for negative probabilities, we’re really just relaxing the positivity condition on the measures we want to consider, right? Now, I have vague recollections of a theorem (associated with names like Hahn and Jordan, maybe?) that says you can decompose such a measure into a positive and negative part so that
Now, both terms in the decomposition should be un-normalized probability measures, i.e., both are positive and
and
and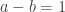 , so that
, so that 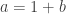 . So, as long as neither
. So, as long as neither  nor
nor  are zero, it seems that such a measure can be interpreted as a simple comparison between two probability measures with different (but related) normalizations. However, I'm not sure such an interpretation is useful in any way….
are zero, it seems that such a measure can be interpreted as a simple comparison between two probability measures with different (but related) normalizations. However, I'm not sure such an interpretation is useful in any way….
All the math you cited is right. The decomposition of a signed measure into its positive and negative part
into its positive and negative part 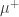 and
and 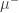 is called the Jordan decomposition, and it’s a spinoff of the Hahn decomposition of the measure space
is called the Jordan decomposition, and it’s a spinoff of the Hahn decomposition of the measure space  into a subset
into a subset 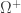 where
where  is positive and a subset
is positive and a subset 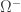 where
where  is negative.
is negative.
I think Burgin wants to think of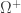 as the set of ‘events’ and
as the set of ‘events’ and 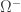 as the set of ‘negative events’… but I don’t understand the concept of ‘negative event’.
as the set of ‘negative events’… but I don’t understand the concept of ‘negative event’.
Going a little further along the lines of my last comment, you can define probability measures
and
Then,
where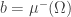 .
.
You could as well ask about negative volume. One important thing when I was studying stochastic analysis were positivity preserving semigroups on measure spaces. From these all relevant random variables arise via Kologorov’s projective limit. I guess negative volume would spoil the way to Dirichlet forms, from whence an implicit differential structure arises. Dirichlet forms (Beurling-Deny criteria in Reed-Simon) need some positivity.
(Apropos: Being overworked I’m currently not conciously following you. But I’m eager to see one day what you get at. Back in my days Kolmogorov’s projective made me have vague halluzinations of category theory…)
I once heard a physicist who was trying to gain a big picture understanding of the many dark matter models out there say something like, ” I am aiming to build a model that represents an unbiased consideration of all possibilities.” I think that could be a general characteristic of a good scientific attitude, “unbiased consideration of all possibilities.” It is something that Quantum Mechanics taught us in its infancy and that Feynman taught us again with the path integral formulation: If it goes through both slits, why not infinitely many slits.
It is often our intuition and experience that creates in our worldview a ‘bias’.
Perhaps that is one way to think of negative probabilities. Instead of thinking of bias as assigning to a possibility a probability that is less than the true value, bias (or negative probability) is some sort of discounting where the underlying probability gets docked.
Well, we can simply redefine all the probability by multiplying it by -1 and voila – an easy to interpret negative probability theory. Or if we want both signs just shift it so that -1 never happens, 0 half the time and 1 always, surely one can make a consistent probability theory that way?
It’s only when we want to attach negative probability to the regular probability theory without modifying it that we run into problems. And it’s hardly surprising, it’s more a rule than an exception that of the countless ways in which existing practical mathematical models of reality can be extended only very few actually turn out to be useful.
When I was a young physicist I studied a probabilistic dynamical system, a motion on a tetrahedron:
that can be considered like a projection of a motion on a sphere:
where
and there are possible constraints on the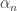 parameter.
parameter.
If there is not constraints on the probability value, then the motion is on a infinite plane, and it is not possible the projection from a sphere, but from a quadratic surface: it is possible to consider the extended-probability like a point on a plane in n-dimensional space.
I have not found real applications for probabilistic dynamics, so it is more complex a real system with dynamic probabilistic negative.
A reader kindly sent me a scan of a typewritten version of Feynman’s paper “Negative Probabilities”. As usual, Feynman is incredibly clear, and he gives some nice examples of how to use negative probabilities. It’s sad how copyright law has made this paper hard to find and held back understanding of negative probabilities for all these years.
I sent it through an optical character recognition program, but since it still takes a lot of manual labor to create something readable, let me just quote two chunks, which are presumably small enough to count as ‘fair use’:
[…]
I decided to add this material and more to the actual blog article, as a kind of public service. But then Michael Nielsen pointed out that preprint version of Feynman’s paper someone sent me is publicly available. Great!
The last equation seems a bit odd … There’s x on the left but not on the right …
Your differential equation has (X,t) where I believe it should be P(x,t).
Yes, sorry, that was a typo. It should be the usual heat equation. Fixed!
There is an interesting analogy in the history of mathematics regarding imaginary numbers, according to a lecture I recently heard. The claim is that they were discovered by Italian mathematicians in the Renaissance in the course of solving equations of the 3rd degree. It happens that the solution of 3rd degree polynomial equations with 3 real roots involves intermediate steps with imaginary numbers. Like Feynman, this didn’t bother them. They didn’t think about them a lot, other than as formal entities required to do the algebra, which eventually disappeared. They had no interest in developing a theory of them, which came (if memory serves) at least 2 centuries later.
Since no-one else has said it: down with “negative probabilities”. The concept is invincibly meaningless. Negative numbers, complex numbers, etc, might appear as an intermediate step in the calculation of a probability, but they can never *be* probabilities.
One of the features of mathematical culture in recent centuries has been the formalization of various concepts, followed by the generalization of the formalism beyond the point where it can be meaningfully be said to be about the original concept, followed by the assertion that the generalized formalism represents a generalized version of the original concept. Thus noneuclidean geometry, noncommutative geometry, nonclassical logic, negative probability, etc.
Eventually there will have to be a reckoning, in which some attempt is made to judge which of these generalizations make sense as a concept and not just as math, and which of them has definitely passed beyond the bounds of sense.
So does it please you that I think of quantum physics not with negative probability theory but instead with noncommutative probability theory? At least I am making a judgement.
Does this not depend on conventional interpretations? This only seems true if you insist that 0 must mean “will never happen” and 1 means “will always happen”. While that will still be true in many contexts, the idea may generalize to cases where the interpretation of 0 weakens enough to be pushed past. I can’t have -1 apples, period. On the other hand I can also never really end up with a “negative amount of money”, but there is a useful way of interpreting such an idea.
Since probability is about “what fraction of the time is this happening?”, and 0 is “not at all”, the context here would (at first glance) need some idea of “anti-happening”, stronger than simply not happening at all. Presumably, like with money, this would really mean trading off with some other external system, where both share a certain amount of “probability resource”, and (again like money) may not make any sense otherwise. I’m not so sure that it can be blithely dismissed, since your dismissal applies just as well to many other applications of negative numbers. No one has minted a negative dollar, or moved in a negative direction, but we’re perfectly happy to act as if they have when the need arises.
I am thinking a simple system with negative probability.
A box divided in two part full of balls (this remind me a Rovelli idea, or Maxwell idea): the ball can cross a wall with a door, and a single particle can cross the door for each instant, and each crossing transport constant energy (the constant chemical energy of the balls, to semplify).
The frequentist count the balls to obtain probability, and the number is ever positive; but if we count the particle that leaves a part like one hole (a negative count), then the energy of the particle is positive, and the probability is negative (so that there is reduction of energy).
There are hole, and ever the same particles, in each part; but the number that must be considered is the sum of particles and holes (negative count) to obtain the mean value.
The mean energy is the energy in the part.
Yes, this is a nice simple example, very analogous to the original use of negative numbers in the accounting of debts.
Recently, a series has appeared on Azimuth about an analogy between stochastic mechanics and quantum mechanics, where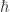 corresponds to inverse bunch size. In the Wigner distribution, the negative quasiprobabilities in phase space are constrained to areas of less than a few
corresponds to inverse bunch size. In the Wigner distribution, the negative quasiprobabilities in phase space are constrained to areas of less than a few 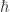 .
.
In the quantum mechanics of photons, coherent states (eigenstates of the annihilation operator) have positive quasiprobabilities everywhere in the Wigner distribution, while Fock states (eigenstates of the number operator) have negative quasiprobabilities somewhere in phase space for n>0. What does this mean in the stochastic mechanics analogy? In order to create a Fock state by adding together coherent states, one may require negative coefficients for some of the coherent states. Does this mean that one cannot always create a nontrivial Fock state of a chemical reaction network unless one has access to anti-matter chemicals?
I’m glad you saw the secret connection between this article and the network theory series! Earlier, Jacob Biamonte was interested in how, when we look at Schrödinger’s equation or the heat equation on a graph, the eigenfunctions of the graph Laplacian are allowed quantum states, but they’re not all allowed stochastic states, since they aren’t all nonnegative functions.
In fact, if a graph is connected, the ground state is the only nonnegative eigenfunction of the graph Laplacian. But we can build other nonnegative functions by taking linear combinations of the ground state and sufficiently small amounts of other eigenfunctions.
Thus, it instantly caught my attention when Feynman pointed out the same idea for the heat equation on the unit interval!
Actually the Fock basis states are all physically allowed in stochastic mechanics. The state
corresponds to having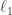 molecules of the first species,
molecules of the first species, 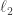 molecules of the second species and so on. Every stochastic state is a normalized nonnegative linear combination of these.
molecules of the second species and so on. Every stochastic state is a normalized nonnegative linear combination of these.
The coherent states
is a normalized positive linear combination of the Fock states when the numbers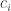 are nonnegative. So these are physically allowed in stochastic mechanics, but as a consequence of the Fock states being the ‘basic’ physically allowed states.
are nonnegative. So these are physically allowed in stochastic mechanics, but as a consequence of the Fock states being the ‘basic’ physically allowed states.
If some of the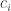 are negative, then we get negative probabilities. That’s when we run into trouble.
are negative, then we get negative probabilities. That’s when we run into trouble.
By the way, you wrote:
I just want to mention that the crucial third part of the series is yet to come.
I think, the interpretation of negative probabilities one can find also in behaviorism, somewhere in the near of intransitive preferences. It should be something like that:
Suppose at some fair there is a tent with an instant lottery. For $10 they offer you to try your luck and win a big teddy-bear. The rules are the following. First you choose randomly a ball from a bag where is white balls and
white balls and 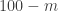 black balls. If you have a white ball you win the prize, but if you have a black ball they can decide still to give you the bear. But only if they want, in the case of black ball there is no guarantee. Thus, probability of winning the price is unknown but more or equal to
black balls. If you have a white ball you win the prize, but if you have a black ball they can decide still to give you the bear. But only if they want, in the case of black ball there is no guarantee. Thus, probability of winning the price is unknown but more or equal to  .
.
Denote this probability as . The question is how many people will agree to take part in the lottery depending on
. The question is how many people will agree to take part in the lottery depending on  . In other words, what is the probability
. In other words, what is the probability  that some visitor takes part giving on the probability to win is more or equal some
that some visitor takes part giving on the probability to win is more or equal some 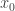 .
.
If we suppose the visitors are fully rational we should expect that increases monotonically from
increases monotonically from  to some
to some 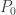 , where
, where 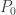 is the fraction of people that participate in the lottery when they are satisfied with its conditions. We can normalize this function and introduce
is the fraction of people that participate in the lottery when they are satisfied with its conditions. We can normalize this function and introduce 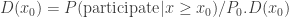 is a monotonic function from 0 to 1 and we can consider it as a probability distribution. Then we can calculate the probability density function
is a monotonic function from 0 to 1 and we can consider it as a probability distribution. Then we can calculate the probability density function  . We can interpret it as follows:
. We can interpret it as follows: 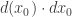 is the portion of people who will agree to participate in the lottery when you increase the “guaranteed” probability from
is the portion of people who will agree to participate in the lottery when you increase the “guaranteed” probability from 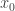 to
to 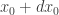 , divided to
, divided to 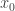 .
.
But the problem is that the people is not rational in the sense that they can be intransitive in their preference on risk. When risk is too big and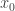 is small nobody will participate. As we increase
is small nobody will participate. As we increase 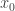 more and more people will want to try their luck. But when there is no risk or it is too small, people will think that organizers simply want to sell them a useless toy for 10$ and many of them will refuse. Thus,
more and more people will want to try their luck. But when there is no risk or it is too small, people will think that organizers simply want to sell them a useless toy for 10$ and many of them will refuse. Thus, 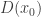 will have a strict maximum between 0 and 1. And this means that the “probability density function”
will have a strict maximum between 0 and 1. And this means that the “probability density function”  , defined above, in some points will be negative.
, defined above, in some points will be negative.
Scott Aaronson is an enthusiast of negativity:
I find this a bit confusing because there’s a perfectly fine mathematical subject called real quantum mechanics where the wavefunction is real, not complex. So, amplitudes can be negative… but we take their absolute value squared to get probabilities, just as in complex quantum mechanics. If you’re trying to teach quantum mechanics while keeping the math simple to the point of avoiding complex numbers, real quantum mechanics could be an interesting pedagogical tool. I suspect this is what Scott is talking about. But it’s conceptually different than allowing negative probabilities.
(There is also quaternionic quantum mechanics, and some nice theorems about why real, complex and quaternionic quantum mechanics are all ‘equally good’ in some respects, but not others, which I discussed here.)
Seems like nonstandard analysis, where to calculate you move into an “enlarged” model for the calculations because in addition to all standard statements you get to use nonstandard statements. Then after the calculation is complete, you go back to the standard model for the answer. What would the enlarged model be that includes both positive and negative probabilities?
Lee wrote:
Yes, Feynman’s discussion of negative probabilities, which seems the clearest to me, treats them as auxiliary quantities that you’re only allowed to use in certain circumstances. Most importantly, if the ‘final answer’ in a calculation is the probability of an event you can actually detect, it has to be nonnegative. But negative probabilities can appear in intermediate steps.
As mentioned in my blog article, the math for that ‘enlarged model’ is already quite standard: it’s the theory of signed measures, which most math grad students learn when they take a course on real analysis. So, the question is just how to interpret this math correctly in probability theory.
On interpretation maybe an example of what I was thinking about nonstandard analysis is relevant. Here was my reply to your post about my use of complex numbers to interpret *possibilities* or vice versa. It might fit better here.
***
John, there’s more. If I’m granted the above statements about *possibility* and also two more, then I can see a difference between the Schrodinger picture and the Heisenberg picture. I hope there’s nothing wrong with my eyesight!
First I have to add the statement “Every possibility that exists has a probability.” This seems compatible with the idea in Barwise’s “Information and Impossibilities” that the same *state* can model either a possibility or an impossibility but not both at the same time. So for example when a possibility occupying a Petri net place is destroyed by the firing of its downstream PN transition and the corresponding impossibility is then created in a downstream PN place, to me this means that a complex number modeling possibility is zeroed and therefore its associated probability is also zeroed.
Second I very much like what the student of Born, Herbert Green, said in his book “Matrix Mechanics” (for which Born wrote the forward). In particular he said something basic about probability. To me it looks like an interpretation that experts might call “frequentist.” Probability isn’t a continuously changing function of time in this presentation of the Heisenberg picture. Instead, it’s a constant value for some finite situation.
Then the difference that comes into focus for me between the Schrodinger and Heisenberg pictures is simply that a kind of infomorphism exists in the Heisenberg picture which does not exist in the Schrodinger picture. I’ve been calling it “the Born infomorphism.” This is a technical term, I’ll attempt to lay it out, and then with this to point at, use more everyday terms.
The Born infomorphism models *time* in a nonstandard way.
For the standard way of looking at *time* I imagine it as a point moving on a line. First I have to imagine that the line exists. Then to imagine that the point is moving on the line, I have to imagine a direction in which it will move between the two alternatives. Since I and others read text from left to right, the choice of left-to-right easily wins. Still, this is something I have to imagine as already occurred– before I can imagine that time is a point moving on this line. And I usually also imagine that it’s drawn on some flat 2D surface. Where does all this stuff come from? It’s like the moving images in a motion picture. Each frame that’s being projected is still, but when flashed one after the other my imagination goes to work and I see the point moving on the line. The motion occurs in my imagination, not in the projected still images.
By analogy, for the film of still frames that produces in my imagination time as a point moving on a line, I start with the Barwise and Moss characterization “the cyclical nature of time” via a couple of examples:
\begin{equation*} seasons = (spring, ( summer, ( fall, (winter, seasons )))) \end{equation*}
\begin{equation*} week = ( Su, ( M, ( Tu, ( W, ( Th, ( Fri, ( Sat, week ) ) ) ) ) ) ) \end{equation*}
Then I go a bit further:
\begin{equation*} now = ( day, now) \end{equation*}
And even further:
\begin{equation*} now = ( second, now) \end{equation*}
And then, what follows is the film of still images being projected and showing up in my imagination as a point moving on a line, although actually the point is still while the line moves:
\begin{equation*} now = ( nonstdMonad, now) \end{equation*}
This stream involves the nonstandard monad, where each unique standard part of the monad has nonstandard infinitesimal parts before and after it. There’s an an old article from Scientific American that explains it best, to me at least.
From here I start laying out the infomorphism–
\begin{equation*}
(stdPart – dt) \mapsto (stdPart + dt)
\end{equation*}
Where stdPart is the unique standard part of the monad, and -dt and +dt are nonstandard parts of the monad before and after it. I need this mirroring function to begin seeing the infomorphism. What I’m looking for is a unique closed path that leads back to the same point I started from. I like to call (stdPart + dt) the nonstandard future and (stdPart – dt) the nonstandard past.
Here’s another part of the closed path of the infomorphism:
\begin{equation*} c = complexNumberForPossibility \end{equation*}
\begin{equation*}
nonstandardFuture \models c
\end{equation*}
And another:
\begin{equation*} P = realNumberForFrequentistProbability \end{equation*}
\begin{equation*}
nonStandardPast \models P
\end{equation*}
And now to close the path:
\begin{equation*}
P = c \times c^ \ast
\end{equation*}
Of course I can’t close the path for the Schrodinger picture because
\begin{equation*}
P(t – dt)\\ \ne \\ c(t + dt) \\ \times \\ c^\ast(t + dt)
\end{equation*}
So the Born infomorphism exists in the Heisenberg picture, but not the Schrodinger picture.
In everyday terms, the Born infomorphism is a perfect translation between statements in a language about the nonstandard future into statements in a language about the nonstandard past.
In other words, its a *prediction*. Possibility in the nonstandard future predicts frequentist probability in the nonstandard past.
Sorry if this seems off-topic, but mention of Feynman and negative probabilities (as conveniences in intermediate calculational steps) reminds me of Feynman’s earlier rejection of creation and annihilation operators as unphysical (and therefore not meaningful), and then getting over this block (cf. Mitchell Porter’s objections). From his Nobel Prize lecture:
Sorry, I botched the Latex
I think a Bayesian could have a negative ‘degree of belief’ in some proposition, while still having the probabilities that some alternative is true sum to 1. They would happily update according to Bayes’ rule so long as they avoid data such that the marginal likelihood sums to exactly zero. (Division by the marginal likelihood is necessary to normalize the posterior distribution.) But leaving aside some specially symmetric situation the marginal likelihood will practically never be exactly zero. For the sake of argument, perhaps this might be relied upon as well as, say, the second law of thermodynamics.
Encountering strong evidence for a hypothesis assigned negative probability would appropriately flip belief to positive probability, with a compensating flip of other beliefs to negative probability.
Why would a Bayesian start with negative probabilities in their prior? Why not? Choosing a prior is a notoriously arbitrary process!
This would result in some oddities. It would allow a Bayesian to calculate an expected value of a variable larger than any value they believe possible. But perhaps this is the sort of feature that could find applications which go beyond conventional probability?
Illustrations of negative probability by two members of the Haskell programming language community:
http://blog.sigfpe.com/2008/04/negative-probabilities.html
http://lukepalmer.wordpress.com/2009/10/21/maximum-entropy-and-negative-probability/
I’m working on a Haskell library for machine learning that relies on negative probability distributions. The idea is to give distributions group structure. For continuous distributions, the binary operation is just adding the raw moments together, and the inverse is making the raw moments negative. The resulting inverse distribution generates negative probabilities using the standard formulas.
There’s some decent pictures in my blog posts that make this all pretty obvious. Here’s one about the normal distribution, and one about the categorical distribution.
To paraphrase the old joke:
A biologist, a physicist and a probabilist stake out a building.
One person enters the building and two leave.
Biologist: “they reproduced”
Physicist: “experimental error”
Probabilist: “if one more person enters, the building will be empty”
It all ad-hoc…but, what about thinking of negative probabilities setting a reference point, a little bit similar like absolute temperature relative to the celsius scale? So if 0 means “does not happen at all”, -1 would still mean, “does not happen at all”, but in the first case you need a probability difference of 1 to get to the case of “surely happens” whereas in the second case you need a difference of 2. Maybe there are some weird physical problems which match to such a description. I remember hearing once that spin 1/2 means something like flipping around two times in full to come back to the original state?
The other thing maybe interesting could be the interpretation of negative probabilities in cases where one does multiply different probabilities for independent events. Then one instance of multiplication would turn the probability somehow “around” while a second negative probability would restore the physical plausible picture. Maybe, this means, that negative probabilities should only occur in pairs, to give meaningful results.
Only spontaneous thoughts, I have to admit, and maybe not very well founded at all…enjoy nevertheless…
Although I will be reading Feynman’s paper now, what about the discussion of probabilities in the initial chapters of E.T. Jaynes’ book?
He proves that probabilities could either be from 0 to 1 or from infinity to 1, and according to the desiderata he considers, these are the only choices.
Do you think that a change in the desiderata will let us have negative probabilities? In the banking case, we had to change our assumption that each person could only have positive money, to allow for situations where money was owed.
Also, as -ve probabilities do appear in intermediate steps, should we also start thinking about probabilities greater than 1, as calculations can be rearranged to show whatever numbers we want?
Hi.
I don’t have an answer to your question, but you may be interested in this paper
http://www.cs.washington.edu/research/jair/abstracts/halpern99a.html
and its follow-up
http://www.cs.washington.edu/research/jair/abstracts/halpern99b.html
which give a critical review of the assumptions (both explicit and implicit) in the proof of Cox’s theorem.
Arjun wrote:
I think you’ll find Jaynes’ ideas are compatible with Feynman’s when they’re both interpreted wisely. It’s really crucial that Feynman says:
Arjun wrote:
Yes, if the probability of an event happening is < 0 the probability of it not happening is > 1, and Feynman considers probabilities greater than 1 in his article.
John, great post. As usual, reading Feynman is like breathing fresh air for the first time in ages. I had a thought connection with your statement: “So, you could say negative numbers were invented to formalize the idea of debt and make accounting easier. Bankers couldn’t really get rich if negative money didn’t exist.”
Have you read David Graeber’s “Debt: The First 5000 Years”? He argues that the idea of debt precedes that of money.
http://www.harvard.com/book/9781612191294_debt_the_first_5000_years/
“Here anthropologist David Graeber presents a stunning reversal of conventional wisdom: he shows that before there was money, there was debt. For more than 5,000 years, since the beginnings of the first agrarian empires, humans have used elaborate credit systems to buy and sell goods—that is, long before the invention of coins or cash. It is in this era, Graeber argues, that we also first encounter a society divided into debtors and creditors.”
He also argues that debt forgiveness can be an important factor in fighting climate change, one of the other major topic of this blog. I thought you might enjoy this if you’ve not seen it already. Cheers.
Negative probabilities play an important role in this paper, presented in QPL this summer : “No-Signalling Is Equivalent To Free Choice of Measurements”” The result hints at an interpretation of negative probabilities.
I recently came across this book by P. Muldowney : A Modern Theory of Random Variation. Which presents a fomrulation of probability theory using the Henstock integral as a basic building block. This approach is indeed deeply fascinating, and extends the notion of “probability” to take on, for example, complex values. Also, from chapter 1 “This extension of classical probability make it possible to bring the Feynman theory of the path integrals whitin the scope of a theory of random variation”
If you haven’t seen it I can recommend at least browsing through the preface and the introduction.
Did anyone else here read this book, comments on it?
I found this great article from 2013 posts of Azimuth blog. I didn’t understand it completely but I should say that is amazing! I really enjoy it. I […]
Feynman seems to hint that the infinities that occur in quantum physics and need to be renormalized are a direct result of forcing all probabilities to be nonnegative. Has anyone tried to apply negative probabilities to quantum field theories? And does this really remove the need for renormalization? That has always seemed the most ad hoc part of QED.
When renormalization was first developed it seemed ad hoc, but now we understand the physical meaning of it, e.g.:
• John Baez, Struggles with the continuum (part 6).
• John Baez, Renormalization made easy.
This fact combined with its remarkable success at predicting results of experiments means few people are trying to get rid of it. Certainly nobody knows how to do so without eliminating its successes. I haven’t heard of attempts to do this by allowing negative probabilities.
Suppose we have a water tank with two parallel pipes, each with a valve, that join at a common outlet. Both valves are open. Then we could say that with probability 1 there will be water at the outlet. But would it not be better to say the probability of water is 2, to capture the fact that after closing one valve we still get water (probability 1) and both valves have to be closed before the probability of getting water is 0?
Similarly, suppose we have a water tank with a single pipe, but with two valves. Both are closed. Then we could say that the probability of getting water at the outlet is 0. But wouldn’t it be better to say that the probability is -1, to capture the fact that if one valve is opened there is still no water (probability 0), and it takes two valves to be open to get water (probability 1)?
Generalizing a bit, probabilities greater than 1 arise when there are multiple ways for something to happen, while negative probabilities arise when there are multiple obstructions to something happening.
[…] In 1987 Richard Feynman wrote an article arguing in favor for negative probabilities. The question should not be: “do they exist?” but rather: “are they useful?”. People have for centuries denied the existence of negative numbers – but thinking about negative money as debts is undeniably useful. How would you do that with negative probabilities? The idea is to loosen the requirement that probabilities must be strictly positive in every calculation and just require the end result to be positive. If you are interested, check out this blog post that has a very nice overview. […]
The magnitude squared of a split-complex number is negative. So if you replace the role of complex numbers in quantum mechanics / quantum computing with split-complex numbers, then you’d end up with negative probabilities.