Before we dive into the exciting world of El Niño prediction, and ways that you can help, let’s have a very very basic crash course on the physics of El Niño.
El Niños are still rather mysterious. But that doesn’t mean we should ignore what the experts know, or suspect.
The basics
Winds called trade winds blow west across the tropical Pacific, from the Americas to Asia. During La Niña years, water at the ocean’s surface moves along with the wind, warming up in the sunlight as it travels. So, warm water collects at the ocean’s surface off the coast of Asia. This creates more clouds and rainstorms there.
Meanwhile, since surface water is being dragged west by the wind, cold water from below gets pulled up to take its place in the eastern Pacific, off the coast of South America.
So, the temperature at the ocean’s surface looks like this:
This situation is actually reinforced by a feedback loop. Since the ocean’s surface is warmer near Asia, it heats the air and makes it rise. This helps the trade winds blow toward Asia: they go there to fill the ‘gap’ left by rising air.
Of course, you should be wondering: why do the trade winds blow west in the first place?
Without an answer to this, the story so far would work just as well if we switched the words ‘west’ and ‘east’. That wouldn’t mean the story is wrong. It might just mean that there were two stable states of the Earth’s climate: a La Niña state where the trade winds blow west, and another state—say, the El Niño—where they blow east. One could imagine a world permanently stuck in one of these phases. Or perhaps it could flip between these two phases for some reason.
Something roughly like the last choice is actually true. But it’s not so simple: there’s not a complete symmetry between west and east!
Why not? Mainly because the Earth is turning to the east. Air near the equator warms up and rises, so new air from more northern or southern regions moves in to take its place. But because the Earth is fatter at the equator, the equator is moving faster to the east. So, this new air from other places is moving less quickly by comparison… so as seen by someone standing on the equator, it blows west. This is called the Coriolis effect, and it produces winds like this:
Beware: a wind that blows to the west is called an easterly. So the westward-blowing trade winds I’m talking about are called "northeasterly trades" and "southeasterly trades" on this picture.
It’s also good to remember that the west Pacific touches the part of Asia also called the ‘Far East’, while the east Pacific touches the part of America also called the ‘West Coast’. So, it’s easy to get confused! If you find yourself getting confused, just repeat this sentence:
Everything will instantly become much clearer.
Terminology aside, the story so far should be clear. The trade winds have a good intrinsic reason to blow west, but in the La Niña phase they’re also part of a feedback loop where they make the western Pacific warmer… which in turn helps the trade winds blow west.
But now comes an El Niño! Now for some reason the westward winds weaken. This lets the built-up warm water in the western Pacific slosh back east. And with weaker westward winds, less cold water is pulled up to the surface in the eastern Pacific. So, the eastern Pacific warms up. This makes for more clouds and rain in the eastern Pacific—that’s when we get floods in Southern California. And with the ocean warmer in the eastern Pacific, hot air rises there, which tends to counteract the westward winds even more.
In other words, all the feedbacks reverse themselves! Here’s how it looked in the big El Niño of 1997:
But note: the trade winds never mainly blow east. Even during an El Niño they still blow west, just a bit less. So, the climate is not flip-flopping between two symmetrical alternatives. It’s flip-flopping between two asymmetrical alternatives.
Here’s how it goes! The vertical height of the ocean is exaggerated here to show how water piles up:
Here we see the change in trade winds and ocean currents:
By the way, you can click on any of the pictures to get more information.
But why?
One huge remaining question is: why do the trade winds weaken? We could also ask the same question about the start of the La Niña phase: why do the trade winds get stronger then?
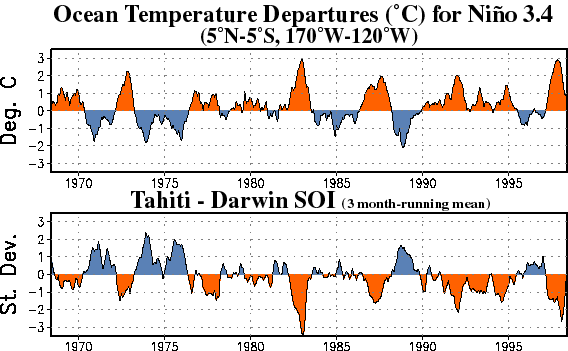
The short answer is: nobody knows! At least there’s no one story that everyone agrees on. There are actually several stories… and perhaps more than one of them is true. So, at this point it is worthwhile revisiting some actual data:
The top graph shows variations in the water temperature of the tropical Eastern Pacific ocean. When it’s hot we have El Niños: those are the red hills in the top graph. The blue valleys are La Niñas. Note that it’s possible to have two El Niños in a row without an intervening La Niña, or vice versa!
The bottom graph shows the Southern Oscillation Index or SOI. This is basically the air pressure in Tahiti minus the air pressure in Darwin, Australia, divided by its standard deviation.
So, when the SOI is high, the air pressure is higher in the east Pacific than in the west Pacific. This is what we expect in an La Niña: that’s why the westward trade winds are strong then! Conversely, the SOI is low in the El Niño phase. This variation in the SOI is called the Southern Oscillation.
If you look at the graphs above, you’ll see how one looks almost like an upside-down version of the other. So, El Niño/La Niña cycle is tightly linked to the Southern Oscillation.
Another thing you’ll see from is that the ENSO is far from perfectly periodic! Here’s a graph of the Southern Oscillation Index going back a lot further:
So, there’s something inherently irregular about this oscillation. It could be chaotic—meaning that tiny changes amplify as time goes by, making long-term prediction impossible. It could be noisy—meaning that the randomness is mainly due to outside influences. It could be somewhere in between! But nobody is sure.
The graph above was made by William Kessler, an expert on El Nño. His FAQs are worth a look:
• William Kessler, What is El Niño and how does it relate to the usual situation in the tropical Pacific?
• William Kessler, El Niño: How it works, how we observe it.
He describes some theories about why an El Niño starts, and why it ends. These theories involve three additional concepts:
• The thermocline is the border between the warmer surface water in the ocean and the cold deep water, 100 to 200 meters below the surface. During the La Niña phase, warm water is blown to the western Pacific, and cold water is pulled up to the surface of the eastern Pacific. So, the thermocline becomes deeper in the west than the east:
When an El Niño occurs, the thermocline flattens out:
• Oceanic Rossby waves are very low-frequency waves in the ocean’s surface and thermocline. At the ocean’s surface they are only 5 centimeters high, but hundreds of kilometers across. The surface waves are mirrored by waves in the thermocline, which are much taller, 10-50 meters in height. When the surface goes up, the thermocline goes down!
• The Madden-Julian oscillation or MJO is the largest form of variability in the tropical atmosphere on time scales of 30-90 days. It’s a pulse that moves east across the Indian Ocean and Pacific ocean at 4-8 meters/second. It manifests itself as patches of anomalously high rainfall and also anomalously low rainfall. Strong Madden-Julian Oscillations are often seen 6-12 months before an El Niño starts!
With this bit of background, I hope you’re ready for what Kessler wrote in his El Niño FAQ:
There are two main theories at present. The first is that the event is initiated by the reflection from the western boundary of the Pacific of an oceanic Rossby wave (type of low-frequency planetary wave that moves only west). The reflected wave is supposed to lower the thermocline in the west-central Pacific and thereby warm the sea surface temperature by reducing the efficiency of upwelling to cool the surface. Then that makes winds blow towards the (slightly) warmer water and really start the event. The nice part about this theory is that the oceanic Rossby waves can be observed for months before the reflection, which implies that El Niño is predictable.
The other idea is that the trigger is essentially random. The tropical convection (organized large-scale thunderstorm activity) in the rising air tends to occur in bursts that last for about a month, and these bursts propagate out of the Indian Ocean (known as the Madden-Julian Oscillation). Since the storms are geostrophic (rotating according to the turning of the earth, which means they rotate clockwise in the southern hemisphere and counter-clockwise in the north), storm winds on the equator always blow towards the east. If the storms are strong enough, or last long enough, then those eastward winds may be enough to start the sloshing. But specific Madden-Julian Oscillation events are not predictable much in advance (just as specific weather events are not predictable in advance), and so to the extent that this is the main element, then El Niño will not be predictable.
In my opinion both these two processes can be important in different El Niños. Some models that did not have the MJO storms were successful in predicting the events of 1986-87 and 1991-92. That suggests that the Rossby wave part was a main influence at that time. But those same models have failed to predict the events since then, and the westerlies have appeared to come from nowhere. It is also quite possible that these two general sets of ideas are incomplete, and that there are other causes entirely. The fact that we have very intermittent skill at predicting the major turns of the ENSO cycle (as opposed to the very good forecasts that can be made once an event has begun) suggests that there remain important elements that are await explanation.
So it’s complicated!
Next time I’ll talk about a new paper that tries to cut through these complications and predict El Niños more than 6 months in advance, using a simple idea. It’s a great opportunity for programmers to dive in and try to do better. But I think we need to keep the subtleties in mind… at least somewhere in the back of our mind.
Azimuth 
Regarding this animated gif:
Over on G+, Harald Hanche-Olson wrote:
I replied:
It will be interesting if the predictability of ENSO can be eventually increased even more than 6 months. It is tempting because in other domains, such as in solid state physics, the most erratic-looking oscillations and band structures arise from basic interference patterns between the wave function of the electron and the periodic potential of a lattice, i.e. Bloch waves.
So to analogize this to the macro world, if the quasi-period of the ENSO can be cracked in terms of a wave equation and underlying modulation, ala Mathieu equation or Hill equation, then the predictability may be improved.
![\frac{d^2x(t)}{dt^2}+[a-2q\cos(2\omega t)]x(t)=F(t)](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bd%5E2x%28t%29%7D%7Bdt%5E2%7D%2B%5Ba-2q%5Ccos%282%5Comega+t%29%5Dx%28t%29%3DF%28t%29+&bg=ffffff&fg=333333&s=0&c=20201002)
And apparently this approach is used to describe the sloshing of liquids in an excited container. The Mathieu equation is combined with a periodic forcing F(t) to recreate various erratic-looking waveforms [1]. Thus we arrive at a behavior that exists somewhere between perfect periodicity and a chaotic regime, with always the possibility of red noise contributing as well.
[1]J. B. Frandsen, “Sloshing motions in excited tanks,” Journal of Computational Physics, vol. 196, no. 1, pp. 53–87, 2004.
I am very happy to see the Azimuth gang working on this problem as I do think it will eventually get solved as soon as the puzzle pieces start to fit together. I am paging through the Azimuth Forum to catch up and see where I can contribute.
Paul Pukite
To provide some resolution to the above comment. I worked a couple of hours per week on the problem and after several months came up with a model that demonstrates incredible fidelity to the ENSO SOI measurement, from 1880 to the present time. The key forcing factors to the Mathieu equation are the QBO, the Chandler Wobble, and the TSI signal. These are all periodic and also provide the basis for the Mathieu (more accurately Hill) modulation factor.
This answers John’s question in the above blog post:
The bottom line is that ENSO is only quasi-periodic as it depends on the input cyclic forcing factors, the characteristic frequency of the sloshing wave equation, and the modulation. Taken as an aggregate, it is no wonder that this problem was difficult to crack!
I wrote up a research paper on the results and it is on ARXIV
Click to access 1411.0815.pdf
Check the Azimuth Forum for a running play-by-play on the progress made during the course of this offshoot of the El Nino project:
http://forum.azimuthproject.org/discussions
and latest thread
https://forum.azimuthproject.org/discussion/1608/enso-revisit
I am currently at an impasse because it is difficult to get the paper published in a scientific journal, as we all seem to lack any academic or research lab credentials in the climate field. You have to wonder how Seth Carlo Chandler got his results published on the Chandler Wobble, especially when you consider his real job was as an actuary … I guess you have to have connections :)
Paul Pukite
Paul wrote:
Why do you say it’s difficult? Have you tried? If so, what have the responses been?
I suspect the main difficulty will be convincing climate scientists that the quasi-biennial oscillation (QBO), the Chandler Wobble, and the total solar irradiance (TSI) have the potential to be major determinants of the El Niño Southern Oscillation (ENSO).
Just getting the curve to fit won’t be enough to convince them. They’ll want to see evidence that it’s physically plausible: that is, calculations based on physics explaining how these causes could create the observed ENSO. For example, it would be good to see a kind of ‘energy budget’, tracking the flow of energy.
They’ll also want to see a statistical argument showing that the curve fit is statistically significant, not coincidence. The Aikake information criterion might be helpful, though I’m not an expert on it.
Are you interested in those 2 projects? I’d find them pretty interesting. Indeed, only after doing something like this could I say I believe your model, despite how impressively it fits the data.
John, I submitted to Physical Review Letters and it got rejected without review.
The physics is solid IMO and is based on the hydrodynamics of sloshing. The three factors that I am combining are individually cited in the ENSO research literature. QBO is well known as a forcing, the Chandler Wobble is suggested by JPL, and the TSI is hypothesized.
The idea of AIC is that it evaluates the quality of a model by penalizing by the number of free variables available. As it sits, this model has no free variables apart from scaling, so it should rate high on the AIC scale. The statistical significance of the fit is also very high as the likelihood of fixed factors combining to coincidentally match such an erratic time series is close to zero.
Substantiating via an energy flow argument is probably a good idea. The issue is that sloshing of the thermocline (as you are showing with the animated 3D gifs) is very sensitive to the density differences in the upper and lower layers. Consider a stratified oil and water mix in a beaker. It only takes a slight forcing to get that in motion. So what I suspect is happening with the ocean is that the radiation is modulating the density of the upper layer.
That being said, a pragmatic question would be to ask why is it even necessary to provide a complete physical basis? That is especially true if what many people are after is simply a good heuristic. As a heuristic alone, the model beats anything I have seen so far. GCMs create different outcomes every time they are run.
I know Physical Review Letters, and I haven’t seen many papers on this sort of topic—that could be why it got rejected without comment. To succeed in publishing in a journal, I’ve always had to read lots of papers in that journal and make sure my paper ‘fits in’, meaning it’s about a subject that appears in that journal, uses similar methods, is written in a roughly similar style, etc. If you could point me to similar papers in Phys. Rev. Lett., then I could help diagnose what needs to be done to publish a paper like this there. If not, perhaps another journal would be better.
Anyway, one should expect a novel paper to be rejected a couple of times, and this one is novel.
Well, suppose you found a wonderful fit between the Southern Oscillation Index and the price of a certain stock. This would be very hard to publish, because people would think it was a coincidence (unless the company sold raincoats or something). People want to see more than a curve matching another curve: they want to be convinced that there’s a good reason.
John,
The reason I picked PRL is because they published a paper by Tsonis and Swanson called “Topology and Predictability of El Niño and La Niña Networks” in Jan 2008.
There was also this later that year:
• “Climate Networks around the Globe are Significantly Affected by El Niño”, K. Yamasaki, A. Gozolchiani, and S. Havlin, Phys. Rev. Lett. 100, 228501, 5 June 2008
PRL is a prestige journal, and they will publish groundbreaking work in any physics-related discipline. After reading the Tsonis paper and being underwhelmed by his findings, I thought I would give it a chance.
Agree that if I try to sell it as a heuristic, it won’t cut it for PRL. The bottom-line is that I am in no hurry to get it published.
I see. Yes, this and the other paper you mention are among the ‘climate networks’ papers we looked at while working on the El Niño project.
The thing is, the ‘network’ methodology used in these papers is fashionable right now among physicists. They’re applying this methodology to everything, right now. I think that’s the main reason these papers got into PRL: applying a fashionable methodology to an important problem is a good way to get into a prestigious journal, regardless of how solid the results actually are.
Okay. So far you seem to be showing little interest in having me, or the rest of the Azimuth gang, help you get it published. If we did this, I think we’d start by performing statistical tests and examining the energy flows to see if we can make a strong case for this theory. It turned out we could, then we’d help you rewrite the paper to include that material, and also adjust the style to maximize the chance of getting in some specific journal (to be determined as soon as possible).
Paul wrote:
It depends how you count them. I think the fair way is to write down the differential equation whereby you compute your estimate of the SOI from the other time series you are using (QBO, Chandler Wobble and TSI). At the very least, this differential equation has some constants in it, which have to be chosen to get a good fit. You have to pay for these constants.
Furthermore, I think you should need to pay in some way for the time series data you are using! Otherwise you could get a better and better fit at little or no cost by using more and more time series.
We can talk to an expert on Aikake Information Criterion to see what they say. But I don’t think they’ll say your model has just 1 free variable.
They may say some variant of the AIC is more suitable for models of this sort, where you are using a formula to compute an estimate of 1 time series from
other time series. I bet such a variant will include a penalty involving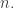 
John,
I will generate the canonical differential equation in a bit. There is not too much to it. I am essentially following the recipe of the sloshing dynamics algorithm, which is a modified Mathieu DiffEq. It is actually a significant simplification in contrast to the charge/discharge delay oscillator that I see mentioned quite often. The latter is intractable as far as getting any meaningful results from.
What is striking is that the sloshing in a volume the size of the tanker likely has similar dynamics to the sloshing of the much larger volume of the Pacific ocean. It won”t be the first or last time that scaling works.
I also tested the approach on coral proxy data which dates back a thousand years. This has been shown to be a sensitive measure of ENSO behavior.
http://contextearth.com/2014/06/25/proxy-confirmation-of-soim/
What is interesting about that blog post is that it was dated within a day of this top-level post and it showed what I was working on when I caught wind of what you guys were working on. So in the last year it has been an essentially a part-time effort to see if I could mature the concept and push it along via the Azimuth Forum.
There is another factor which contributes … Ocean surfaces, even after averaging out waves, are not level. In many instances there is an overall slope, something not very steep, about 1 meter in 100 kilometers, but something which contributes to current flow. This happens because normals to isobaric surfaces are not parallel to gravitational vectors. This situation can be unstable, but it also can be stabilized by an outside force, sometimes the important Coriolis force.
What’s the Coriolis? The easiest way, I think, to visualize Coriolis is to note that on a rotating sphere, the angular velocity of a mass particle at a high latitude is smaller than the velocity of one near the Equator. That’s because the circumference of the circle at latitude L is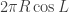
, expressing L in radians and R being the radius of the sphere. Thus 
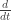of that is
What happens if, starting from a point significantly north of the Equator, because of a current, the particle moves due south? Well, it finds itself among particles which are moving faster west-to-east than it was moving, and, so, it drifts west. The situation is flipped if the particle was initially south of the Equator, but the situation remains that the particle drifts west.
This affects both oceans and atmosphere.
In case you’re interested, here are the other parts of this series:
• El Niño project (part 1): basic introduction to El Niño and our project here.
• El Niño project (part 2): introduction to the physics of El Niño.
• El Niño project (part 3): summary of the work of Ludescher et al.
• El Niño project (part 4): how Graham Jones replicated the work by Ludescher et al, using software written in R.
• El Niño project (part 5): how to download R and use it to get files of climate data.
• El Niño project (part 6): Steve Wenner’s statistical analysis of the work of Ludescher et al.
• El Niño project (part 7): the definition of El Niño.
[…] of course, the pull quote was from a RealClimate introduction I made in 2015 describing how John Carlos Baez had started a project to model ENSO in 2014, in which I have continued to contribute to via Baez’s Azimuth Project […]