guest post by Blake S. Pollard
Over a century ago James Clerk Maxwell created a thought experiment that has helped shape our understanding of the Second Law of Thermodynamics: the law that says entropy can never decrease.
Maxwell’s proposed experiment was simple. Suppose you had a box filled with an ideal gas at equilibrium at some temperature. You stick in an insulating partition, splitting the box into two halves. These two halves are isolated from one another except for one important caveat: somewhere along the partition resides a being capable of opening and closing a door, allowing gas particles to flow between the two halves. This being is also capable of observing the velocities of individual gas particles. Every time a particularly fast molecule is headed towards the door the being opens it, letting fly into the other half of the box. When a slow particle heads towards the door the being keeps it closed. After some time, fast molecules would build up on one side of the box, meaning half the box would heat up! To an observer it would seem like the box, originally at a uniform temperature, would for some reason start splitting up into a hot half and a cold half. This seems to violate the Second Law (as well as all our experience with boxes of gas).
Of course, this apparent violation probably has something to do with positing the existence of intelligent microscopic doormen. This being, and the thought experiment itself, are typically referred to as Maxwell’s demon.
When people cook up situations that seem to violate the Second Law there is typically a simple resolution: you have to consider the whole system! In the case of Maxwell’s demon, while the entropy of the box decreases, the entropy of the system as a whole, demon include, goes up. Precisely quantifying how Maxwell’s demon doesn’t violate the Second Law has led people to a better understanding of the role of information in thermodynamics.
At the American Physical Society March Meeting in San Antonio, Texas, I had the pleasure of hearing some great talks on entropy, information, and the Second Law. Jordan Horowitz, a postdoc at Boston University, gave a talk on his work with Massimiliano Esposito, a researcher at the University of Luxembourg, on how one can understand situations like Maxwell’s demon (and a whole lot more) by analyzing the flow of information between subsystems.
Consider a system made up of two parts, and
. Each subsystem has a discrete set of states. Each systems makes transitions among these discrete states. These dynamics can be modeled as Markov processes. They are interested in modeling the thermodynamics of information flow between subsystems. To this end they consider a bipartite system, meaning that either
transitions or
transitions, never both at the same time. The probability distribution
of the whole system evolves according to the master equation:
where is the rate at which the system transitions from
The ‘bipartite’ condition means that
has the form
The joint system is an open system that satisfies the second law of thermodynamics:
where
is the Shannon entropy of the system, satisfying
and
is the entropy change of the environment.
We want to investigate how the entropy production of the whole system relates to entropy production in the bipartite pieces and
. To this end they define a new flow, the information flow, as the time rate of change of the mutual information
Its time derivative can be split up as
where
and
are the information flows associated with the subsystems and
respectively.
When
a transition in increases the mutual information
meaning that
‘knows’ more about
and vice versa.
We can rewrite the entropy production entering into the second law in terms of these information flows as
where
and similarly for . This gives the following decomposition of entropy production in each subsystem:
where the inequalities hold for each subsystem. To see this, if you write out the left hand side of each inequality you will find that they are both of the form
which is non-negative for .
The interaction between the subsystems is contained entirely in the information flow terms. Neglecting these terms gives rise to situations like Maxwell’s demon where a subsystem seems to violate the second law.
Lots of Markov processes have boring equilibria where there is no net flow among the states. Markov processes also admit non-equilibrium steady states, where there may be some constant flow of information. In this steady state all explicit time derivatives are zero, including the net information flow:
which implies that In this situation the above inequalities become
and
If
then is learning something about
or acting as a sensor. The first inequality
quantifies the minimum amount of energy
must supply to do this sensing. Similarly
bounds the amount of useful energy is available to
as a result of this information transfer.
In their paper Horowitz and Esposito explore a few other examples and show the utility of this simple breakup of a system into two interacting subsystems in explaining various interesting situations in which the flow of information has thermodynamic significance.
For the whole story, read their paper!
• Jordan Horowitz and Massimiliano Esposito, Thermodynamics with continuous information flow, Phys. Rev. X 4 (2014), 031015.


The post is repeated twice.
No, it was only repeated once. But I’ll fix it.
But I’ll fix it.
Great article! However, this post contains an accidental second copy of the whole discussion!
I just wonder how much Maxwell’s demon was inspired by concepts like Sheoll, hell, Hades etc. Wikipedia writes:
Reblogged this on Tambo University and commented:
In the absence of anything of consequence to say about my own work, this post from John Baez’s blog is worth reading in tandem with the post made here last year, regarding Alexandre De Castro’s paper on the one-way Bennett’s thermodynamic engine.
My interest is applicable to built environments and it often appears its descriptive is a lot like Maxwells demon or perhaps an information heat engine, the physics literature is interesting. This is what I noticed;
Biodiverse Cities “Information Heat Engines” Information Entropy: Biodiversity, Energy, and Materials; the Smart Built Environment, a thermodynamic interpretation of living heat engines.
Live systems cannot persist in isolation and the second principle of thermodynamics does not require that abundant free energy simply becomes high entropy along the shortest path: living organisms absorb energy from sun-light or from energy-rich chemical compounds and finally return part of such energy to the environment as entropy (heat and low free-energy compounds such as water and CO2). Andy van den Dobbelsteen : Energy Potential Mapping
Wiki: The general struggle for existence of animate beings is not a struggle for raw materials – these, for organisms, are air, water and soil, all abundantly available – nor for energy which exists in plenty in any body in the form of heat, but a struggle for [negative] entropy, which becomes available through the transition of energy from the hot sun to the cold earth. Austrian physicist Ludwig Boltzmann.
According to James Lovelock, to find signs of life, one must look for a “reduction or a reversal of entropy.” I’d look for an entropy reduction, since this must be a general characteristic of life.
Schrödinger Paradox; prescience “An organism’s astonishing gift of concentrating a stream of order on itself and thus escaping the decay into atomic chaos – of drinking orderliness from a suitable environment – seems to be connected with the presence of the aperiodic solids…” We now know that the ‘aperiodic’ crystal is DNA and that the irregular arrangement is a form of information. “The DNA in the cell nucleus contains the master copy of the software, in duplicate. DNA’s apparent information processing function provides a resolution of the paradox posed by life and the entropy requirement of the second law.
Wiki; In 1982, American biochemist Albert Lehninger argued that the “order” produced within cells as they grow and divide is more than compensated for by the “disorder” they create in their surroundings in the course of growth and division. “Living organisms preserve their internal order by taking from their surroundings free energy, in the form of nutrients or sunlight, and returning to their surroundings an equal amount of energy as heat and entropy.”
Negentropy – a shorthand colloquial phrase for negative entropy.
Ectropy – a measure of the tendency of a dynamical system to do useful work and grow more organized.
Extropy – a metaphorical term defining the extent of a living or organizational system’s intelligence, functional order, vitality, energy, life, experience, and capacity and drive for improvement and growth.
Ecological entropy – a measure of biodiversity in the study of biological ecology. In a study titled “Natural selection for least action” published in the Proceedings of The Royal Society A., Ville Kaila and Arto Annila of the University of Helsinki describe how the second law of thermodynamics can be written as an equation of motion to describe evolution, showing how natural selection and the principle of least action can be connected by expressing natural selection in terms of chemical thermodynamics. In this view, evolution explores possible paths to level differences in energy densities and so increase entropy most rapidly. Thus, an organism serves as an energy transfer mechanism, and beneficial mutations allow successive organisms to transfer more energy within their environment.[20]
Abstract Generative systems are now being proposed for addressing major ecological problems. The Complex Urban Systems Project (CUSP) founded in 2008 at the Queensland University of Technology, emphasizes the ecological significance of the generative global networking of urban environments.
Thanks for your comments. I’ll have to take a look at the paper you mentioned by Ville Kaila and Arto Annila, sounds like interesting stuff related to the more recent post by Marc Harper here on Azimuth.
Blake Pollard wrote, “Every time a particularly fast molecule is headed towards the door the being opens it, letting fly into the other half of the box. When a slow particle heads towards the door the being keeps it closed.”
The being also allows slow particles to flow in the opposite direction.
Now let us suppose that such a vessel is divided into two portions, A and B, by a division in which there is a small hole, and that a being, who can see the individual molecules, opens and closes this hole, so as to allow only the swifter molecules to pass from A to B, and only the slower molecules to pass from B to A.
http://en.wikipedia.org/wiki/Maxwell%27s_demon
I am thinking that there is a problem with the statement that the entropy cannot decrease.
In a spherical box, filled with ideal gas, in an equilibrium state, there are fluctuations of entropy; if the statement that the entropy cannot decrease was true, then for each ideal arbitrary (in infinite numbers) separation planes, that divide the sphere in half, there would be the same number of molecules that crossing the plane in both directions, with an instantaneous balance (with an absence of dynamic for many particles: too many constraints); I think that it is not necessary a Maxwell’s demon to obtain a flow of particles through a division in a box, it is sufficient an equilibrium point and a temperature different from absolute zero, and the fluctuations make the demon, in some instants.
I have some questions. For starters, about this:
As you know very well, entropy is only nondecreasing for a certain class of Markov processes, for example the doubly stochastic ones. Otherwise we need to use relative entropy. So why is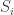 nondecreasing?
nondecreasing?
I guess I’m a bit confused about the definition of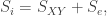 too. You didn’t say what
too. You didn’t say what 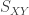 and
and 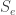 are, did you? It seems you only gave formulas for their time derivatives.
are, did you? It seems you only gave formulas for their time derivatives.
Also — why the decision to study the open system? Why not (also) study the closed system?
A careful reading of the arxiv preprint says this about the environmental entropy change, on page three; I quote:
This almost makes sense to me but not quite: In short, it appears that one needs to be familiar with the modern-day formulation of “stochastic thermodynamics”.
I don’t see a formula for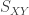 in Blake’s blog article here, just for
in Blake’s blog article here, just for  It might be in the paper, but since I’m his thesis advisor I don’t need to look in the paper: I’m allowed to complain that he should not tell me what the time derivative of a quantity equals before saying what that quantity equals.
It might be in the paper, but since I’m his thesis advisor I don’t need to look in the paper: I’m allowed to complain that he should not tell me what the time derivative of a quantity equals before saying what that quantity equals.
I understand the scary-looking equation you wrote down, but not its supposed consequence.
An equilibrium probability distribution for a continuous-time Markov process obeys ‘detailed balance’ if the rate at which the system hops from the th state to the
th state to the  th state equals the rate at which it hops from the
th state equals the rate at which it hops from the  th to the
th to the  th.
th.
We can turn this into math as follows.Suppose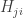 is the probability per time that the system hops from the
is the probability per time that the system hops from the  th state to the
th state to the  th state. Then a probability distribution
th state. Then a probability distribution  obeys detailed balance iff
obeys detailed balance iff
(no sum over repeated indices here). We can always take any probability distribution and write it as a Boltzmann distribution
and write it as a Boltzmann distribution
for some choice of energies at least if
at least if  for all
for all 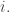
With a little algebra, these equations imply that
and thus
If you apply this to a 2-part system and change the notation a bit, the equation looks fancier:
But the principle is fundamental and important: the log of the ratio of the forward and backward transition rates between two states must be proportional to the energy difference between those states!
In short: we can’t figure out the transition rates using energy considerations alone, but we can figure out ratios of forward versus backward transition rates.
Thank you!
And one minor emphasis/clarification: the used in the derivation of the detailed balance formula is the equilibrium distribution, and not a stand-in for
used in the derivation of the detailed balance formula is the equilibrium distribution, and not a stand-in for  . Since both use the letter p, this can be a source of confusion. The point being that, at equilibrium, the quantity of “things” transitioning into a state must equal the those leaving.
. Since both use the letter p, this can be a source of confusion. The point being that, at equilibrium, the quantity of “things” transitioning into a state must equal the those leaving.
In writing these words, I just realized that the detailed balance formula looks just like Bayes law, but in disguise. Bayesians would say: P(i|j) is the probability of state i given condition j, so that Bayes law is P(i|j) P(j) = P(j|i)P(i) Now, of course, a conditional probability is not a transition rate, but it does suggest that, in some strange sense, the master equation describes “non-equilibrium Bayesian statistics”. Hmmm. Curious. Surely others have noted the resemblance; can one deuce anything wise from it, or is it a gee-whiz thing?
Thanks again; I have a nasty habit of hitting the “post” button before I have finished thinking (or proof-reading). But of course, “non-equilibrium Bayesian statistics” is more-or-less the theory of Markov chains. Doh.
Whoops, I can see my first mistake! Most of the sums should be over and
and 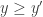 to avoid double counting.
to avoid double counting.
The term is something that has confused me too. For starters,
term is something that has confused me too. For starters,
is the Shannon entropy of the joint system, and
is its time derivative. The other term, is a little trickier. I’m not sure who first introduced it, but Schnakenberg already wrote the entropy production with this extra ‘environment’ term.
is a little trickier. I’m not sure who first introduced it, but Schnakenberg already wrote the entropy production with this extra ‘environment’ term.
Your question about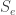 applies to any Markov process, not just bipartite ones. Therefore let me use the simpler notation where
applies to any Markov process, not just bipartite ones. Therefore let me use the simpler notation where  denotes the transition rate from
denotes the transition rate from  to
to  and
and  is the probability of being in the
is the probability of being in the  state. The Shannon entropy is then
state. The Shannon entropy is then
and
To get something of the form
by hand.
If the transition rates are constant, it is the time derivative of
which looks like one half the expectation value of the ‘skewedness’ of transitioning between and
and  . What it doesn’t look like is any entropy I’ve ever seen since it involves the transition rates. If there exists an equilibrium distribution
. What it doesn’t look like is any entropy I’ve ever seen since it involves the transition rates. If there exists an equilibrium distribution  satisfying detailed balance, then
satisfying detailed balance, then
Together this implies that the total entropy is
There is probably a better way to write the second term.
Blake, I’m confused by some of your remarks; John and I discussed this, up above, and obtained what I thought was an entirely satisfactory answer: the system as a whole is attached to a heat bath, and detailed balance with the heat bath provides the environment term (and not the detailed balance for Markov chain all by itself). One cannot obtain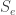 this way, but one can obtain
this way, but one can obtain  , as John sketches. The arxiv paper says as much, it just didn’t quite say it in a way that I immediately recognized.
, as John sketches. The arxiv paper says as much, it just didn’t quite say it in a way that I immediately recognized.
Its not really “physical” to try to reconstruct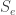 : it’s a heat bath of some indeterminate size, you can’t know what it’s entropy is; you can only know how it changes.
: it’s a heat bath of some indeterminate size, you can’t know what it’s entropy is; you can only know how it changes.
An interesting generalization to this problem would be to attach X and Y to heat baths of different temperatures.
Right. I agree that
has a physical interpretation as rate of change of entropy due to heat flow between the system and the environment, while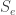 itself has a less clear form and interpretation. Nonetheless you can ask the question what is the time integral of
itself has a less clear form and interpretation. Nonetheless you can ask the question what is the time integral of
and try to make some sense of it. That is all I was doing.
Schnakenberg wrote down the formula for entropy production as one-half the sum of currents
times the affinities
but only part of this quantity is the time derivative of an entropy. He also showed that you can write this using a cycle basis as a sum over cycles instead of summing over all pairs of states.
Thanks, Blake! I can’t help but see another question: when you ask “what is the time integral of (expression)”, it seems to me that the time-integral will be history-dependent: i.e. it will depend on the specific values that the take over time; different paths would seem to yield different values for that integral. I don’t see how it couldn’t be history-dependent.
take over time; different paths would seem to yield different values for that integral. I don’t see how it couldn’t be history-dependent.
So, if I wander into that rabbit-hole … to actually obtain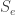 from that expression, you would have to perform a path integral, summing over all paths. I’m going to take a wild stab here, at the path integral; it might look like this:
from that expression, you would have to perform a path integral, summing over all paths. I’m going to take a wild stab here, at the path integral; it might look like this:
where the![\int [dp]](https://s0.wp.com/latex.php?latex=%5Cint+%5Bdp%5D+&bg=ffffff&fg=333333&s=0&c=20201002) says “average over all possible paths that each
says “average over all possible paths that each  can take”. Although the above does not really look correct; it doesn’t take the canonical form of path integral; the canonical form is exp-trace-log. So really, it should resemble something like this:
can take”. Although the above does not really look correct; it doesn’t take the canonical form of path integral; the canonical form is exp-trace-log. So really, it should resemble something like this:
I probably wrote that wrong. Z is then the partition function, so that , more or less, up to whatever errors I made in writing this all down.
, more or less, up to whatever errors I made in writing this all down.
Here’s a kind-of off-the-wall question, please bear with me: in non-equilibrium thermodynamics, where a system is constantly pumped with energy (has a hot and cold end), its been observed that, in nature, such systems tend to settle into a state where entropy production is maximized. When I say “observed” I mean “observed by ecologists”, who use some rather shady-looking formulas that “explain” atmospheric dynamics, soil erosion, and the like, based on temperature gradients driven by solar radiation. When I say “shady-looking”, I mean “formulas I don’t understand, despite their superficial resemblance to those in undergrad thermodynamics textbooks”. But the overall idea seems intriguing, (hey! entropy production maximization! Wow!) so I’ve been watching out for more rigorous/mathematical models & descriptions of the basic idea.
So, my question is: can this model be used to give any insight?
To paraphrase the ecologists claim: in their driven systems, they have it that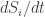 is itself increasing over time, i.e. that
is itself increasing over time, i.e. that  is positive. So: under what circumstances might this happen in this model? What would the analog of the “temperature gradient” be, which seems to be an important ingredient for forcing
is positive. So: under what circumstances might this happen in this model? What would the analog of the “temperature gradient” be, which seems to be an important ingredient for forcing  to be positive?
to be positive?
That is great question/comment! I’m still learning a lot of this stuff myself. Part of my goal on my dissertation journey is to understand all the different ‘min/max entropy’ and ‘min/max entropy production’ principles and how they are related to one another. Ecologists, molecular biologists, stochastic thermodynamicists, and others provide a slew of interesting examples to look at. Lots of them use diagrams or networks to represent the systems they are studying so hopefully it all fits together as part of a nice picture!
It will fit into a nice picture—and your job is to figure out as much as possible about this picture and write it up in your thesis, starting today!
Here is an article: Route to thermalization in the α-Fermi-Pasta-Ulam system which looks on a first glance like being connected to your considerations.
I may have another example of what the authors of this paper call a “bipartite” system. It’s in a paper for a physics contest at FXQI.org titled “Simple Math for Questions to Physicists.” There it’s called the “Born Infomorphism.”
http://fqxi.org/community/forum/topic/2420
The rigorous math supporting all the natural talk in this contest paper about “informational flow” is, at its foundations in the references, Category Theory. In these references, Category Theory has been applied by the authors to create Channel Theory. We read about the “information channels” by virtue of which “information flows” in the world of Channel Theory.
(About Channel Theory– as stated by the authors of Information Flow: The Logic of Distributed Systems (p 31): “In a more general setting, these infomorphisms are known in computer science as Chu transformations…So one could look at this book as an application of Chu spaces and Chu transformations to a theory of information.” Chu spaces are a category.)
But in the paper “Thermodynamics with Continuous Information Flow,” the mathematical language is based on Shannon-like formulas and axioms from thermodynamics. This– is a completely different mathematical language. However, it also supports talk about “information flow.”
Here we have two different kinds of mathematics, talking about the same words–
“information flow.”
Leading perhaps to a question that might be of interest:
Is one of these mathematical languages stronger than the other for talking about information? If so, which is stronger? Is it Channel Theory, as in the references for “Simple Math for Questions to Physicists”? Or is it Shannon’s theory, combined with the laws of thermodynamics in “Thermodynamics with Continuous Information Flow”?
In Channel Theory an inquiry about the comparative strength of two mathematical languages would go something like this (p 31):
“…let us think about the example of number theory considered as a part of set theory. Applying example 2.2, suppose that L1 is the language of arithmetic, with numerals 0 and 1 and additional nonlogical symbols like <,+,x,=, and so on. By the tokens of L1 we mean any structure that satisfies the basic axioms PA of Peano arithmetic; the types are sentences formulated using the above symbols plus standard symbols from logic. Let L2 be the language of set theory, with only \in sign and = as nonlogical symbols. By the tokens of L2 we mean any structure that satisfies the usual axioms ZFC of Zermelo-Fraenkel set theory; again types are sentences formulated in terms of \in , =, and the basic symbols of logic.”
“One of the standard themes in any course on set theory is to show how to translate number theory into set theory using the finite von Neumann ordinals. Formally, what is going on is the development of an “interpretation.” One shows how to translate any sentence of number theory into a sentence of set theory.”
“At the level of structures, though, things go the other way. A model of number theory does not determine a unique model of set theory. Indeed, some models of number theory are not parts of any models of set theory at all, because set theory is much stronger than number theory. By contrast, any model of set theory does determine a unique model of number theory. The reversal of directions is quite important.”
Given this example, do you think that the following steps could be a practical approach for finding out whether or not one of the above mathematical languages is “stronger” than the other for talking about information– as, in the example, set theory is “stronger” than number theory?
If possible, map every equation from (a) “Thermodynamics with Continuous Information Flow” to (b) sentences in Channel Theory and Informationalism, as found in the references to “Simple Math for Questions to Physicists.”
If possible, map the particular model or structure supporting each of the above sentences (b) in Channel Theory and Informationalism to: the model or structure supporting its original equation in (a).
If it is possible to complete the informorphisms or translations from every equation in (a) to sentences in (b), as well as contra-wise the corresponding models– but impossible the other way around– then (b) is “stronger” than (a).
Or, it might go the other way. In that case (a) is “stronger” than (b).
Probably would not get a clean answer, of course. In that case, here is another question:
Are these two languages part of a single “information channel”? (p 76)