I think of sulfur and phosphorus as clever chameleons of the periodic table: both come in many different forms, called allotropes. There’s white phosphorus, red phosphorus, violet phosphorus and black phosphorus:
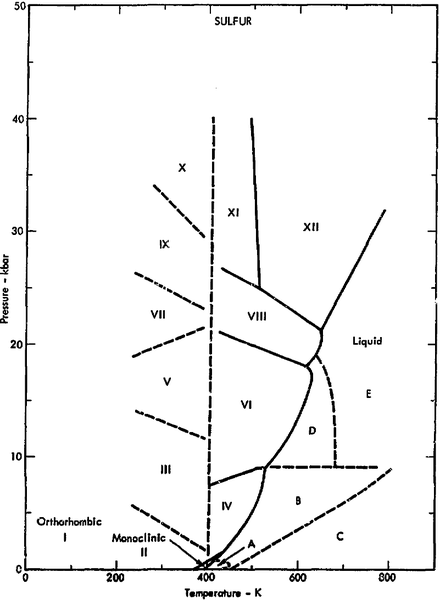
and there are about two dozen allotropes of sulfur, with a phase diagram like this:
So I should have guessed that sulfur and phosphorus combine to make many different compounds. But I never thought about this until yesterday!
I’m a great fan of diamonds, not for their monetary value but for the math of their crystal structure:
In a diamond the carbon atoms do not form a lattice in the strict mathematical sense (which is more restrictive than the sense of this word in crystallography). The reason is that there aren’t translational symmetries carrying any atom to any other. Instead, there are two lattices of atoms, shown as red and blue in this picture by Greg Egan. Each atom has 4 nearest neighbors arranged at the vertices of a regular tetrahedron; the tetrahedra centered at the blue atoms are ‘right-side up’, while those centered at the red atoms are ‘upside down’.
Having thought about this a lot, I was happy to read about adamantane. It’s a compound with 10 carbons and 16 hydrogens. There are 4 carbons at the vertices of a regular tetrahedron, and 6 along the edges—but the edges bend out in such a way that the carbons form a tiny piece of a diamond crystal:
or more abstractly, focusing on the carbons and their bonds:
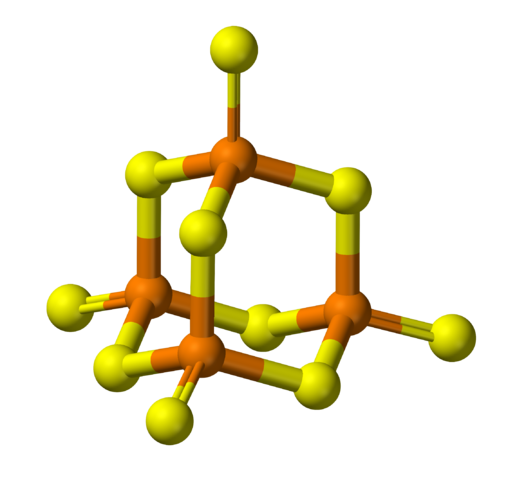
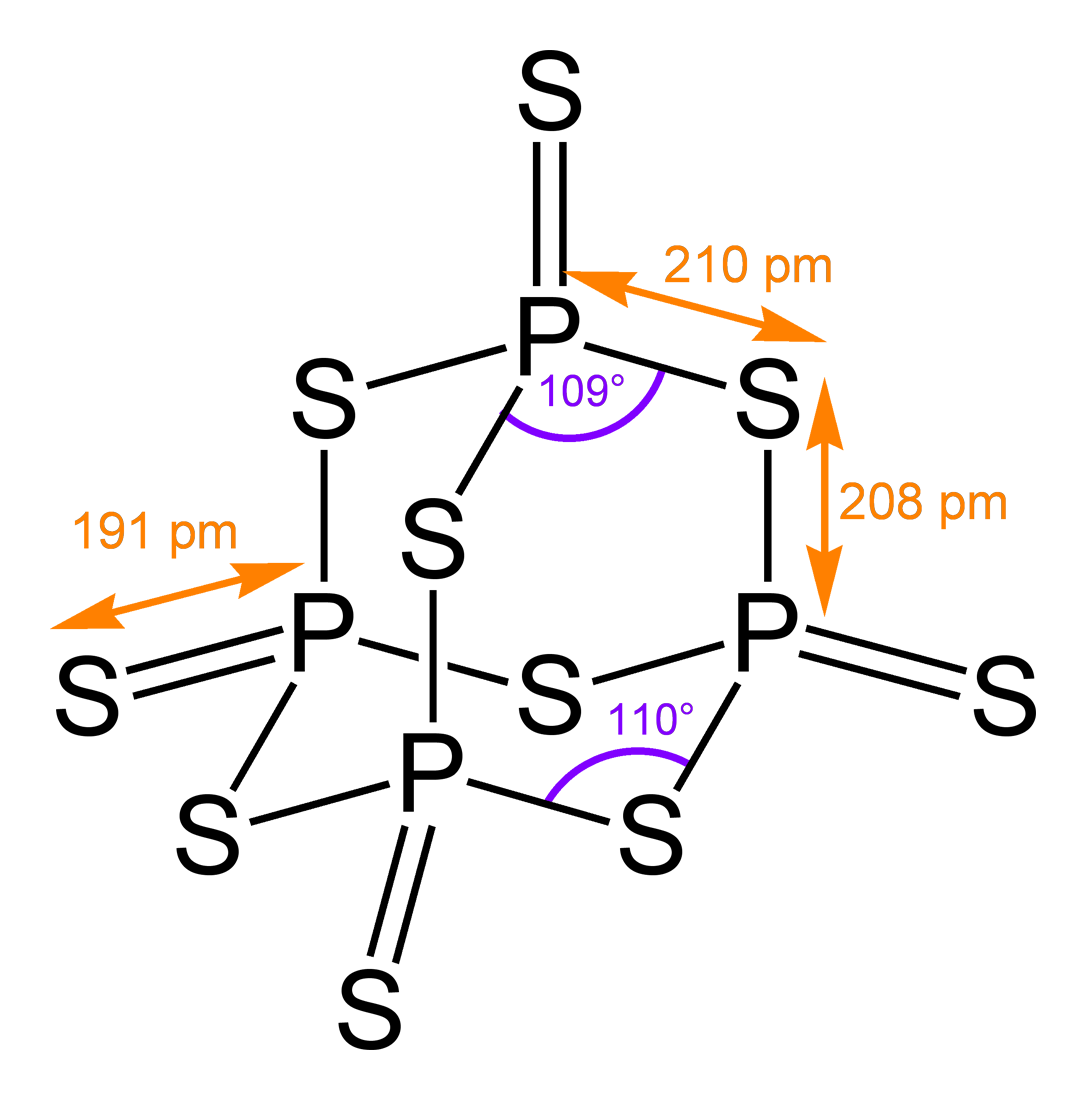
Yesterday I learned that phosphorus decasulfide, P4S10, follows the same pattern:
The angles deviate slightly from the value of
that we’d have in a fragment of a mathematically ideal diamond crystal, but that’s to be expected.
It turns out there are lots of other phosphorus sulfides! Here are some of them:
Puzzle 1. Why do each of these compounds have exactly 4 phosphorus atoms?
I don’t know the answer! I can’t believe it’s impossible to form phosphorus–sulfur compounds with some other number of phosphorus atoms, but the Wikipedia article containing this chart says
All known molecular phosphorus sulfides contain a tetrahedral array of four phosphorus atoms. P4S2 is also known but is unstable above −30 °C.
All these phosphorus sulfides contain at most 10 sulfur atoms. If we remove one sulfur from phosphorus decasulfide we can get this:
This is the ‘alpha form’ of P4S9. There’s also a beta form, shown in the chart above.
Some of the phosphorus sulfides have pleasing symmetries, like the
alpha form of P4S4:
or the epsilon form of P4S6:
Others look awkward. The alpha form of P4S5 is an ungainly beast:
They all seem to have a few things in common:
• There are 4 phosphorus atoms.
• Each phosphorus atom is connected to 3 or 4 atoms, at most one of which is phosphorus.
• Each sulfur atom is connected to 1 or 2 atoms, which must all be phosphorus.
The pictures seem pretty consistent about showing a ‘double bond’ when a sulfur atom is connected to just 1 phosphorus. However, they don’t show a double bond when a phosphorus atom is connected to just 3 sulfurs.
Puzzle 2. Can you draw molecules obeying the 3 rules listed above that aren’t on the chart?
Of all the phosphorus sulfides, P4S10 is not only the biggest and most symmetrical, it’s also the most widely used. Humans make thousands of tons of the stuff! It’s used for producing organic sulfur compounds.
People also make P4S3: it’s used in strike-anywhere matches. This molecule is not on the chart I showed you, and it also violates one of the rules I made up:
Somewhat confusingly, P4S10 is not only called phosphorus decasulfide: it’s also called phosphorus pentasulfide. Similarly, P4S3 is called phosphorus sesquisulfide. Since the prefix ‘sesqui-’ means ‘one and a half’, there seems to be some kind of division by 2 going on here.











Thank you John, you’re helping me understand (learn) a lot more about atomic structure than i did before i found your blog! :-)
For example, and as a way of answering some of Q1. The element phosphorus in it’s natural (or is that refined?) state, because of it’s outer electron structure forms bonds with 3 other phosphorus atoms to make a tetrahedrally shaped P4. Each P atom donates a single outer electron with 3 others, binding them together in the most ‘efficient’ form in 3 dimensions—a tetrahedral pyramid. Each P atom also has a lone pairing of electrons it could use to form other bonds but in the absence of any other atoms these pairs prefer not to attach to other P atoms to make more complicated and higher energy level structures.
So P4 is the base the sulphides are created from.
Since the sulphides have one more electron in their outer shell (=6) than phosphorus they tend to form bonds that complete their outer octet by receiving, more easily than by donating, electrons and so will accept bonds from either one (double electron sharing) or two other atoms. The double sharing is easily achieved by the ‘spare’ pairing of electrons each atom in P4 has after donating 3 to the other P atoms in the tetrahedron.
So P tends to donate an electron to fill an orbital/octal while S tends to receive them. P has a total of 5 electrons to donate but will usually give up 3 first and holds on harder to the last 2. The penta in pentasulphide comes from the 5 electrons phosphorus V shares with only sulphide atoms in the molecule while the sesqui refers to the 3 electrons phosphorus 111 shares equally with one of two other atoms (P or S) in the molecule.
I had originally thought the molecule P4S10 should have been named phosphorus tetrasulphide since each P has 4 other atoms it bonds to but it is the electrons not the atoms that give us the prefix.
I’ll leave the maths and the drawing of other potential molecules to those more qualified than my humble self ;-)
love.
P.S. The diamond up/down symmetry comes about because of the unevenly matched energy levels of the outer electrons in the carbon atom. Although it has 4 outer electrons to donate/receive there are two pairs with slightly different energy potentials (2s and 2p) this gives a slightly unbalanced tetrahedron when all four electrons are being shared as 2 (the s orbitals) are held closer to the nucleus than the other 2 (p orbitals) this would make a nearly undetectable difference in the lattice dimensions but may allow for greater stability when combining many such atoms together.
It might help visualise this if you see the shape of a tetrahedron not as perfectly symmetrical but as a composition of nearly identical pairs of atoms—2 being above and at right angles to the bottom two. if when next to a similar atom the higher energy electron (upper level pair) matches with its counterpart then i think i’m correct in thinking this will result in a structure that has atoms that have every third planar level matching and reversed from the level above or below it.
Does that make sense to you?
The key with carbon is that while it has 4 electrons to share, they are paired so that one pair is very close to but not exactly identical with the other. Similar to the 3/2 ratio of electrons in the P example above.
Actually, scratch the last half of the above. While it is true that for a single C atom there are two differing outer e- energies, when they bond with other carbon atoms a slight amount of energy is added to the system such that four equal e energy states are maintained around each C nucleus making all bonds of equal (and therefore tetrahedrally symmetrical) strength/length. There are 4 hybridised sp (unpaired) electron orbitals thus produced rather than the original paired s and unpaired p orbitals.
It is actually no more true to describe the carbon atoms’ tetrahedral bonding as up or down than it is to say any mass of similarly sized marbles are stacked in up and down layers because they touch each other in a similar tetrahedral contact point set thus making offset layers with each other in four differing planes.
lwbut wrote:
It’s hard for me to agree or disagree, because sentences like “P is actually no more true than Q” blow the gaskets of my mathematical mind. I can handle things being true or false, but “no more true than” is a slippery concept.
Here’s what I was alluding to in my article. In the face-centered cubic—one of the infinitely many densest ways to pack spheres in 3 dimensions—the spheres are centered at points of a lattice.
And here I’m using lattice in the mathematical sense, which is more restrictive than how crystallographers use it: it’s a set of points in n-dimensional space such that if p and q are in this set, so are p+q and p-q. This implies that the lattice has enough translational symmetries to carry any point in this set to any other.
On the other hand, the so-called ‘diamond lattice’, better called the diamond cubic, is not a lattice. Instead it’s the union of two different lattices, each of which is a face-centered cubic. One of them consists of the red dots in this picture, while the other consists of the blue dots:
To see this, note that this structure has no translational symmetry carrying one of the red dots to one of the blue dots.
Thanks for the expansion John, and the patience you extend to me :-)
Thanks to my consideration of the cuboctahedron (skeletal) model i have made i feel i am better able to understand the concepts of face centred versus diamond cubic lattice structures – at least physically if not quite mathematically ;-) I saw where you were going with the red and blue lattices as being ‘different’, even though every atom in the structure is identical to every other atom, albeit with the orientation of their immediate four interconections being mirror reversed to that of all four neighbours. Is there not a mathematical symmetry in there somewhere, if not with the atoms themselves then how about around the point equidistant between any two atoms? Mirror symmetry?
Going back to the cuboctahedron it describes not only a sphere, and cube in 3D space it also consists of two mirror symmetrical (like the diamond lattice) tetrahedra. All four of which share a common central point. There is at the same time 6 identical pentahedra – square sided pyramids – with the same common point and oriented around the x,y and z axes of 3d space. This quite remarkable structure has revealed yet another feature (factor) to me today. It is relatively easy to see factors such as 0,1,2,3,4 and 6 as features in the cuboctagon, 0 being the centre or origin in 3d space, 1 being the basic unit from the centre to the periphery of the sphere or cube, 2 equal halves, 3 sided equilateral triangles on it’s surface or it’s 3 dimensional symmetry etc. but i could not see a way of factoring it by 5 before. (this was important to me because of my hobby of photographing Flora – 4 and 6 petalled flowers are common but there seem to me to be more 5 petalled ones. Thanks to the cuboctahedron and a close relative – the Rubik cube i finally was able to see how 5 and 10 can be factored into the picture.
This is in part thanks to your posts forcing me to think harder on the topic :-)
love.
Phosphorus selenide: “The isoelectronic anion [Ge4Se10]4- which has the adamantane like P4O10 structure is known, an example is the sodium salt Na4Ge4Se10.”
Naming conventions like “diphosphorus trisulfide” may lead to civil unrest like dihydrogen monoxide. Trying to learn crystallography is difficult when there are so many aliases like trapezohedron (AKA tetragon-trioctahedron) or trisoctahedron (AKA trigonal trisoctahedron) (but it doesn’t seem as bad as paleontology). And those bond angles lead to Pop. Sci. advertisements like the one in the last issue claiming to have altered the H-O-H bond angle in water molecules.
Not quite as bent is “crystal healing” (which I suspect started with a 1950-70s Analog sci-fi magazine article about “self-repairing” crystals that self-repaired broken corners after being reimmersed in a suitable super-saturated solution).
But why for instance does a diamond seem to have only a single Raman peak at about 1332 cm-1 and how could I possibly use such a spectrum to deduce the 3d structure of a diamond? Or more generally what is it exactly about the mathematics of diamonds that is more interesting than that of say the different polymorphs (phases?) of “ice”?
The mathematics of ice is interesting because it’s complex; the mathematics of diamond is interesting because it’s simple, yet it hints at the glory of the E8 lattice in 8 dimensions.
Paraphrasing what I said back in “week193”:
If this seems complicated, it’s vastly simpler than the mathematics of ice, which I touched on here:
• Ice, Azimuth, 15 April 2012.
Scroll down to read an approximate calculation of the entropy of ordinary hexagonal ice due to ‘proton disorder’.
E8 (mathmatics):
“Root lattice (maximal torus) of rank 8 of the E8 root system:
a Lie group of dimension 248, containing 240 root vectors spanning R8.”
Many years ago I tried to describe an “asteroid of revolution” (cusp fusion reactor)
to a blind girl using four pennies arranged in a square on a table and then telling her
to imagine rotating the central void around either the x or y axis. She seemed to enjoy
the puzzle. When it comes to these higher dimensions (space or group) I tend to go blind and
start thinking in terms of cube databases,
or dynamic videos evolving in space-time like Finnegan’s Wake.
Sam Loyd’s tangram paradoxes.
Frustrated protons? Why are clathrate hydrides hard to mine?
I am thinking that could be possible to obtain more unstable molecules from the general molecules using a diffusion of phosphorus in the pattern, so that if the valence of the phosphorus is different from the valence of the sulfur, then there could be a double bound (or triple bound); so that I think that there are many more pattern, using only a replacement of sulfur atoms with phosphorus atoms, and this could be obtained (in the real world) using a low density diffusion of phosphorus molecules in phosphorus sulfides (like in the doping), obtaining a different surface structure; if the number of phosphorus atom is low in the structure, then I think that the functional of the Hamiltonian does not change much.
The same could be obtained from the allotropes of the sulfur (that are 30), with a low density diffusion.
“Each phosphorus atom is connected to 3 or 4 atoms, at most one of which is phosphorus.”
This seems to be false for the “ungainly beast” alpha form of P4S5, in which one of the phosphorus atoms (in the lower right in your rendering) is connected to two Ps and an S:
(It also seems false for several of the other molecules in the chart, namely P4S4 beta and P4S6 alpha and gamma, which have a similar-looking shape.)
Sadly I don’t know nearly enough chemistry to be able to make headway on any of these puzzles (though lwbut’s comment above sounds like a good explanation for the first). Looking forward to reading more about these neat little molecules!
You’re right—I’d not noticed those examples where a phosphorus connects to two other phosphori (phosphoruses??). So that rule of thumb is not a strict rule, though it may count as a ‘tendency’.
I’d wanted to mention that besides P4S3:
there’s an even more dramatic exception to this tendency, namely white phosphorus, which is simply P4 with no sulfur!
But this is somewhat unstable: the bonds don’t want to be bent at such a sharp angle, so there’s a lot of energy in the strained bonds. If you leave white phosphorus sitting around in sunlight at room temperature and pressure, it gradually turns into red phosphorus, which is an amorphous network sort of like this:
If you leave white phosphorus sitting in air in the dark, it slowly oxidizes, glowing greenish-white—hence the name phosphorus.
(Someone should make some better pictures of the structure of red phosphorus for Wikicommons, following the same conventions as the rest of the the pictures!)
The question of the plural of phosphorus amuses me greatly (phosporodes?). According to Collins, it is indeed phosphori. https://www.collinsdictionary.com/dictionary/english/phosphori
I’m relieved to know that someone has already weighed in on the plural of ‘phosphorus’. People often complain of pedantry when it comes to issues of spelling and grammar, but really, it’s much better to give pedantry fairly harmless outlets like this.
Zincblende is the name you all are groping for.
I don’t think we’re groping for anything: I, at least, have been saying exactly what I want to say. But zincblende is indeed a nice crystal whose two kinds of atoms lie at the two face-centered cube lattices in the diamond cubic:
That is the lattice that just about all of optoelectronics and high-speed cellular technology is built from :)
I am thinking that molecules could be described by a n-ple of numbered vectors with zero sum, so that the sequence of displacements give a chemical structure: a closed path that touch each atoms of the molecules; it is like a graphical representation of the molecules. It seem equal to the seven bridge of Konigsberg problem in a threedimensional path (if the number of vectors must be minimum).
I am thinking that if the n-ple vectors are a tile in a three dimensional space, then the n-ple cover the whole space, without the Bravais primitive vectors.
It could be possible to obtain each crystal structure using a closed path, and it could be possible to write each organic compound in a unique way (it is not the simplest, if there are many functional groups).
“sesqui” doesn’t only mean 3/2 . “sesquialtera” means 3/2 . “sesqui” by itself means N+1/N . sesquitertia means 4/3, sesquiquarta means 5/4, etc. This goes back to Greek numerology that assigned a mystical importance to superparticular ratios, i.e. those of the form N+1/N .
Never heard of those until now. From what I can find in the OED, “sesquitertia” and “sesquiquarta” (which actually isn’t even in my OED, although I can find it online) are rarely used outside music theory; for example, sesquiquarta for the 5:4 ratio may refer to a major third interval, or sesquitertia might be used to refer to a 4 against 3 rhythm.
The prefix sesqui- comes from semi (half) + que (and, or also), so another half more or 3/2, and so the default meaning, rooted in that etymology, is surely just that, 3/2. The sesquitertia etc. smells to me like a back formation.