I have a new favorite molecule: adamantane. As you probably know, someone is said to be ‘adamant’ if they are unshakeable, immovable, inflexible, unwavering, uncompromising, resolute, resolved, determined, firm, rigid, or steadfast. But ‘adamant’ is also a legendary mineral, and the etymology is the same as that for ‘diamond’.
The molecule adamantane, shown above, features 10 carbon atoms arranged just like a small portion of a diamond crystal! It’s a bit easier to see this if you ignore the 16 hydrogen atoms and focus on the carbon atoms and bonds between those:
It’s a somewhat strange shape.
Puzzle 1. Give a clear, elegant description of this shape.
Puzzle 2. What is its symmetry group? This is really two questions: I’m asking about the symmetry group of this shape as an abstract graph, but also the symmetry group of this graph as embedded in 3d Euclidean space, counting both rotations and reflections.
Puzzle 3. How many ‘kinds’ of carbon atoms does adamantane have? In other words, when we let the symmetry group of this graph act on the set of vertices, how many orbits are there? (Again this is really two questions, depending on which symmetry group we use.)
Puzzle 4. How many kinds of bonds between carbon atoms does adamantane have? In other words, when we let the symmetry group of this graph act on the set of edges, how many orbits are there? (Again, this is really two questions.)
You can see the relation between adamantane and a diamond if you look carefully at a diamond crystal, as shown in this image by H. K. D. H. Bhadeshia:
or this one by Greg Egan:
Even with these pictures at hand, I find it a bit tough to see the adamantane pattern lurking in the diamond! Look again:
Adamantane has an interesting history. The possibility of its existence was first suggested by a chemist named Decker at a conference in 1924. Decker called this molecule ‘decaterpene’, and registered surprise that nobody had made it yet. After some failed attempts, it was first synthesized by the Croatian-Swiss chemist Vladimir Prelog in 1941. He later won the Nobel prize for his work on stereochemistry.
However, long before it was synthesized, adamantane was isolated from petroleum by the Czech chemists Landa, Machacek and Mzourek! They did it in 1932. They only managed to make a few milligrams of the stuff, but we now know that petroleum naturally contains between .0001% and 0.03% adamantane!
Adamantane can be crystallized:
but ironically, the crystals are rather soft. It’s all that hydrogen. It’s also amusing that adamantane has an odor: supposedly it smells like camphor!
Adamantane is just the simplest of the molecules called diamondoids.
These are a few:
1 is adamantane.
2 is called diamantane.
3 is called triamantane.
4 is called isotetramantane, and it comes in two mirror-image forms.
Here are some better pictures of diamantane:
People have done lots of chemical reactions with diamondoids. Here are some things they’ve done with the next one, pentamantane:
Many different diamondoids occur naturally in petroleum. Though the carbon in diamonds is not biological in origin, the carbon in diamondoids found in petroleum is. This was shown by studying ratios of carbon isotopes.
Eric Drexler has proposed using diamondoids for nanotechnology, but he’s talking about larger molecules than those shown here.
For more fun along these lines, try:
• Diamonds and triamonds, Azimuth, 11 April 2016.









Yes, they are interesting molecules. I think adamantane is basically a tetrahedron. The four atoms with three C-C bonds are the vertices, and the sides are just connections via a CH2 group.
So geometrically, the symmetry group is that of a tetrahedron. And there are two kinds of C – vertex and mid-side. Although there isn’t that much difference between them – each has four unstrained tetrahedral bonds.
And there is really only one kind of C-C bond, linking a vertex C and a mid-side C.
The alkane with just the four carbons linked – tetrahedrane – is interesting. Hasn’t been made yet – it seems too strained. But adding a CH2 in each bond takes out all the strain.
Great! To complete answering my questions, the symmetry group of adamantane as an abstract graph is the same as its symmetry group as a geometrical object in Euclidean space: both are the symmetry group of the tetrahedron, namely the symmetric group S4, the group of permutations of 4 things.
Tetrahedrane would be a beautiful thing if it existed:
Out of curiosity, is there a simple physical explanation for why we should consider both rotations and reflections when computing the symmetry group of the molecule as a tetrahedron, in other words, why is it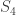 rather than
rather than 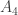 ?
?
For the chemist the point group symmetry of tetrahedrane is not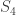 not
not  but
but 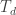 .
.
What is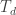 ? Another name for the same 24-element group?
? Another name for the same 24-element group?
Hi, Noam! It’s going a bit far to say we “should” include reflections as well as rotations when discussing the symmetry of a molecule… I’d be content to say we “can”. But since you posed this challenge, I’ll try to argue that we should.
The laws of quantum mechanics relevant to chemistry are symmetrical under the rotation/reflection group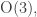 so if a molecule has some subgroup
so if a molecule has some subgroup 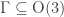 as its symmetry group, this group
as its symmetry group, this group  will have a representation on the Hilbert space describing the ‘vibrational modes’ of that molecule: that is, the ways it can vibrate.
will have a representation on the Hilbert space describing the ‘vibrational modes’ of that molecule: that is, the ways it can vibrate.
The energies of these vibrational modes, and the allowed transitions between vibrational modes, can be studied using the spectrum of the molecule: usually these transitions cause the absorption or emission of infrared light.
So, we can learn interesting things about the infrared spectra of molecules using the representation theory of the group We could use the smaller group
We could use the smaller group  that excludes reflections, but then we’d learn less, since we’d be ignoring the effects of reflection symmetries.
that excludes reflections, but then we’d learn less, since we’d be ignoring the effects of reflection symmetries.
The group is called the point group of a molecule, and chemists have developed a flow chart to allow them to easily determine this group.
is called the point group of a molecule, and chemists have developed a flow chart to allow them to easily determine this group.
You got me interested in the history of this stuff, and here’s a bit from the Wikipedia article on molecular symmetry:
Bethe and Wigner are, of course, heroes of mathematical physics.
By the way, most of the pictures here and in my blog article are from Wikipedia, and you can learn more by clicking on them.
Thank you for the explanation! I think the other question I was trying to formulate was, does chemistry distinguish a molecule from its mirror image? From the links I learned that sometimes it does, actually, and that there is a name for the two halves of such a mirror pair: “enantiomers“. On the other hand, enantiomers have almost identical properties, and can only be distinguished in an “asymmetric environment”:
When present in a symmetric environment, enantiomers have identical chemical and physical properties except for their ability to rotate plane-polarized light (+/−) by equal amounts but in opposite directions (although the polarized light can be considered an asymmetric medium).
[…]
Enantiomer members often have different chemical reactions with other enantiomer substances. Since many biological molecules are enantiomers, there is sometimes a marked difference in the effects of two enantiomers on biological organisms.
Noam wrote:
Yes. I mentioned one in my blog article: ‘isotetramane’, which is number 4 here:
You can see that it’s different from its mirror-image form.
Most biological molecules have this property, too. You may have heard of the sugar called ‘glucose’. This comes in two mirror-image forms. On this planet life mainly uses the right-handed form, called ‘dextrose’. It’s ‘right-handed’ in the sense that the polarization of light passing through a solution of dextrose gets rotated clockwise.
There are very slight inherent differences between enantiomers because the weak nuclear force knows the difference between left and right. Could this be relevant to biology? And why are most people right-handed, anyway? I wrote about these puzzles back in “week73” of This Week’s Finds:
Nick said:
“I think adamantane is basically a tetrahedron.”
Take a silicon wafer and expose the diamond structure surface to dopant surfactants such as arsenic and it will rearrange in all sorts of ways. Same thing happens with germanium. I was the first to observe this years ago in my early research work. Since that time, the semiconductor industry has used this idea for nanotechnology structuring of computing devices.
Nick is quite right in all respects. Each face of the tetrahedron can be thought of as a hexane ring with 3 C atoms being shared with all 3 of its neighbouring hexane rings (Normally C6H12 but with 3 C-H bonds on each ring being replaced by C-C bonds with 3 other rings to form a four sided solid).
And i think you mistakenly stated the number of H atoms as 30 when it can only possibly be 16 (6 CH2 + 4 CH).
Badeisha’s graphic is interesting but confusing in that it includes a C from 4 separate additional diamond atoms in the overall lattice. (Diametrically opposing corners of the cube). The double hexagon shape it contains when viewed from (i suspect 4) different angles is very interesting to me as i am investigating the space-filling and structural forming properties of cuboctagons. When viewed from some angles these objects exactly describe both a cube, a planar hexagon and also a sphere, rather like the animation.
The major difference between the diamondoid and the cuboctagon is that the cuboctagon’s periphery (consisting of 12 interconnected outer vertices/C atoms) is exactly equidistant from a central point (vertex) and that this distance is the same as that connecting all external points to it’s nearest neighbour. The cuboctagon can also be created from 8 symmetrically connected equilateral tetrahedra (or, simultaneously, 6 connected pentahedra).
love.
Fascinating stuff! You’re right, there are just 16 hydrogens in adamanantane. I’ll fix that now.
I was not able to find the word “cuboctagon” anywhere on the internet. Did you mean “cuboctahedron”?
Thanks John – i had a brain fade :-( Cuboctahedron is the term i meant! – not a 2D polygon but a 3D structure i think may lie at the root of all atomic structure, or could explain a lot about how atoms in nature tend to align and bond. For example, using it as a model it is very easy to see how all the electron orbitals up to the energy level of the 3d shell are oriented around a central nucleus.
Apologies for the error and for not having the mathematical skill to be able to explain my fascination in clearer terms ;-)
love. ( or Bob if you prefer.)
A fascinating molecule geometrically similar to adamantane is phosphorus pentoxide:
It crystallizes in a fun way:
Can definitely see the similarities/shared symmetries with adamantine and the fundamental tetrahedronal shape of the 4 phosphorous atoms that is then expanded upon to form the entire molecule. Given that this molecule shares no atom types with that of adamantine its safe to say they share very few other properties, particularly chemical ones.
I see from Wikipedia that the crystallisation forms more into planes than a solid 3D like diamond and wonder why it seems to break its tetrahedron shape and form hexagonal ‘rings’ of 6 interlinked PO4 ion shapes.
love.
Yeah, I don’t fully understand these patterns formed by phosphorus pentoxide:
According to Wikipedia the first image is supposed to show a ‘sheet’, and the second ‘stacked sheets’, but I don’t get it. More information is here:
• D. Stachel, I. Svoboda and H. Fuess, Phosphorus pentoxide at 233 K, Acta Cryst. C51 (June 1995), 1049–1050.
I am thinking that the structure of the diamondoids, with the symmetry, could be represented by the lower degree polynomial in three variables with the same symmetry of the diamondoid: so that with the right parameters could be possible to overlap the level surface with the structure of the diamondoids; so that there could be the symmetry, and the shape of the diamondoids in a single formula.
Bastardane: “A close relative to adamantane and its proper name is ethano-bridged noradamantane. Because its unusual ethano-bridge was a deviation from the standard hydrocarbon caged rearrangements, it came to be known as bastardane—the unwanted child.”
– List of chemical compounds with unusual names
List of character tables for chemically important 3D point groups
Group Theory and Vibrational Spectroscopy
Raman bands explained
Raman Spectroscopy Explained
Yesterday I learned that phosphorus decasulfide, P4S10, follows the same pattern: